How to Write and Graph the Standard Equation of a Circle
The following Standard Equation of a Circle Formula examples will show you everything you need to know!
Welcome to this free lesson guide that accompanies this Standard Equation of a Circle Explained! Tutorial where you will learn the answers to the following key questions and information:
What is the standard equation of a circle definition?
How can I find the equation of a circle given center and radius?
How can I find the equation of a circle given center and diameter?
How can I find the equation of a circle given a graph of the circle?
This Complete Guide to the Standard Equation of a Circle includes several examples, a step-by-step tutorial, an animated video mini-lesson, and a free equation of a circle worksheet and answer key.
*This lesson guide accompanies our animated Standard Equation of a Circle Explained! video on YouTube.
Want more free math lesson guides and videos? Subscribe to our channel for free!
Standard Equation of a Circle Definition
Before you learn the standard equation of a circle formula, let’s quickly review the basic properties of circles:
The radius of a circle is any line that extends from the center of the circle to the edge.
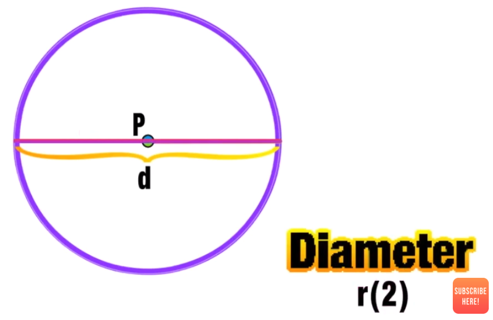
The diameter of a circle is any straight line that extends from one edge of the circle through the center and to the opposite side. The value of the diameter is two times the radius.
Radius = half the length of the diameter
Diameter = twice the length of the radius
The Standard Equation of a Circle Formula:
The standard equation formula of a circle formula above is not as intimidating as it looks.
Let’s break it down:
You only need to know two pieces of information to write the standard equation of a circle:
The Center Point Coordinates (h,k) where h is the x-value and k is the y-value
The length of the radius r
That’s it! Now let’s look at an example:
How to Find the Standard Equation of a Circle Formula
Example 1
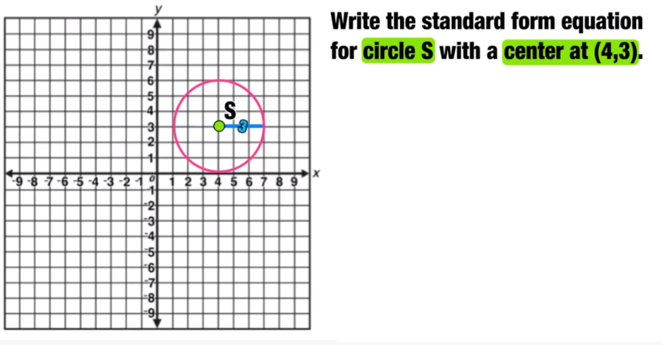
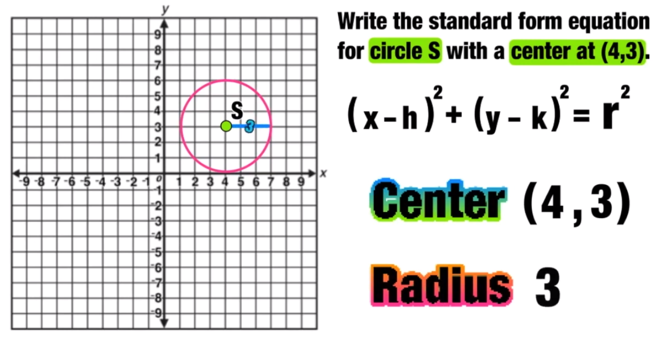
Write the standard form equation for circle S with a center at (4,3).
Remember that you only need two pieces of information to write the standard equation of a circle: the coordinates of the center point, and the length of the radius.
In this example, the center point is at (4,3) and the radius is 3 (you can find the length of the radius by drawing a horizontal line from the center of the circle to the edge and counting the number of spaces).
h=4, k=3, and r=3
Now you can replace h with 4 and k with 3 to complete the left side of the equals sign and then r^2 with 3^2 (which equals 9) to complete the ride side as follows:
This is the standard equation of Circle S
Example 2
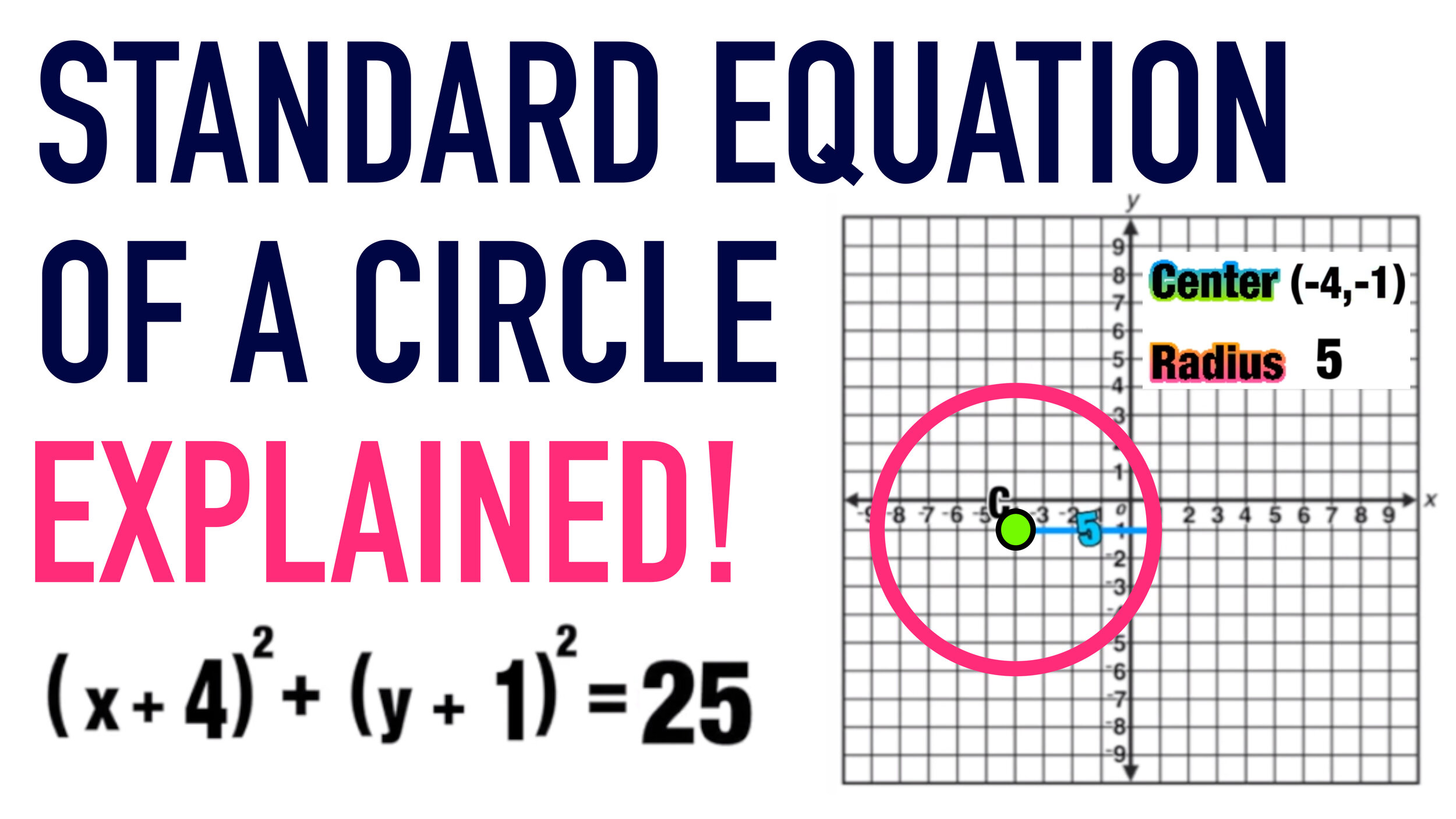
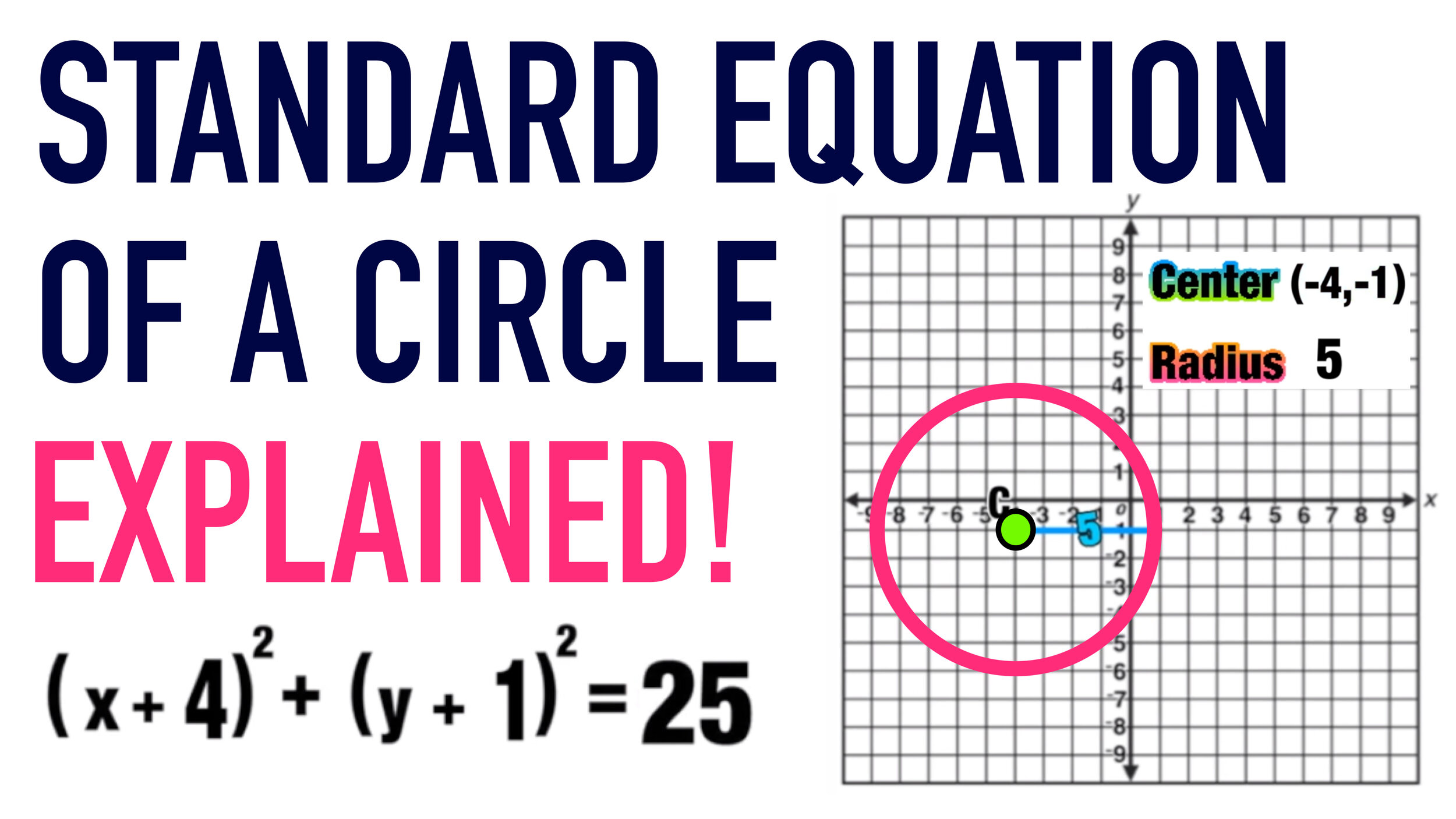
Write the standard form equation for circle C with a center at (-4,-1).
Remember that you only need two pieces of information to write the standard equation of a circle: the coordinates of the center point, and the length of the radius.
In this example, the center point is at (-4,-1) and the radius is 5 (you can find the length of the radius by drawing a horizontal line from the center of the circle to the edge and counting the number of spaces).
Now you can replace h with -4 and k with -1 as follows (remember that two negatives make a positive!) and r with 5 as follows:
Remember that double negatives become positive!
This is the standard equation of Circle C.
EXAMPLE 3
Write the standard form equation for Circle J with a center at the origin and a diameter of 18.
To write the equation of Circle J, you need to know the center coordinates and the length of the radius.
You already know that the center is at the origin, which is (0,0) so h=0 and k=0
And you also know that the diameter is 18, and since a radius equals one half of the diameter, r = 18/2 = 9, so the radius is 9.
Now you can write the equation of the circle as follows:
The graph of Circle J.
This is the standard equation of Circle J.
Example 4
*On this last example, you will work in reverse and identify the center coordinates and radius given the standard equation of a circle.
Start by finding the coordinates of the center of Circle P as follows:
Circle P has a center at (7,0)
Now you just have the find the value of the radius r. The value 196 represents r^2, so, to find the value of r, you have to figure out what number squares equals 196 as follows:
The radius of Circle P is 14 because 14^2 equals 196.
Answer: Circle P has a center at (7,0) and a radius of 14.
The trinomial factors to (x+1)(x+1) or (x+1)^2
Standard Equation of a Circle Formula: Video Tutorial
Still confused? Check out the animated video lesson below:
Check out the video lesson below to learn more about the standard equation of a circle formula and to see more completing the square problems solved step-by-step:
Equation of a Circle Word Problems (Advanced Practice)
Looking for more advanced practice with the standard equation of a circle? The following video lesson covers topics including:
equation of a circle word problems
finding equation of a circle given two points
using distance and midpoint formulas to find the equation of a circle
Extra Practice: Free Equation of a Circle Worksheet
Free Worksheet!
Are you looking for some extra practice? Click the links below to download your free worksheets and answer key:
Equation of a Circle Worksheet:
CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET
Keep Learning with More Free Lesson Guides:
Have thoughts? Share your thoughts in the comments section below!
(Never miss a Mashup Math blog--click here to get our weekly newsletter!)
By Anthony Persico
Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.