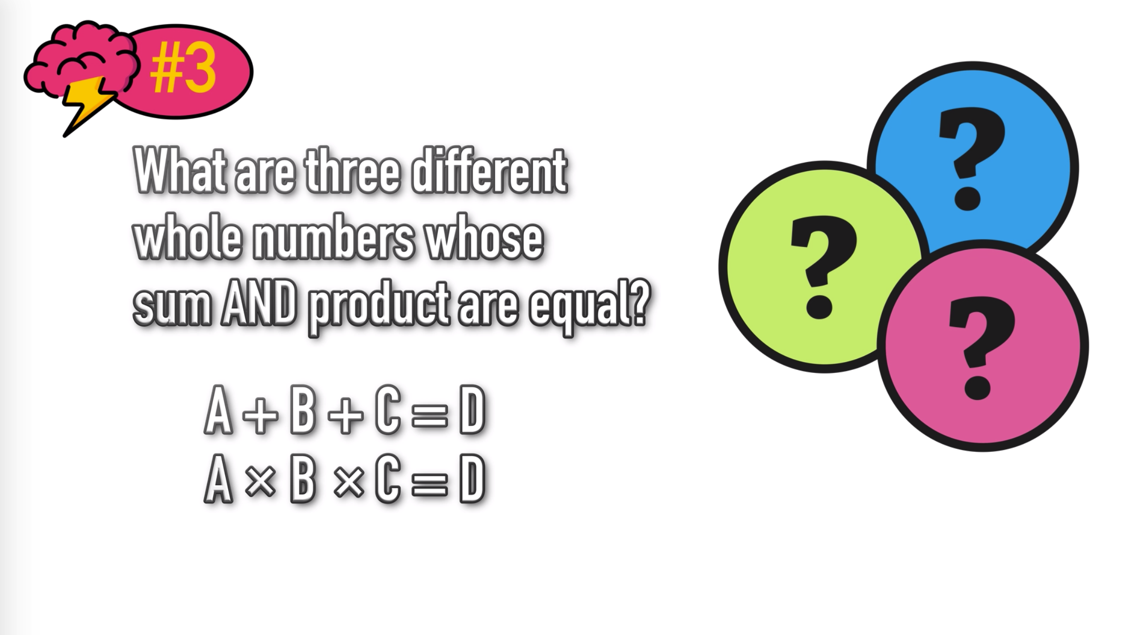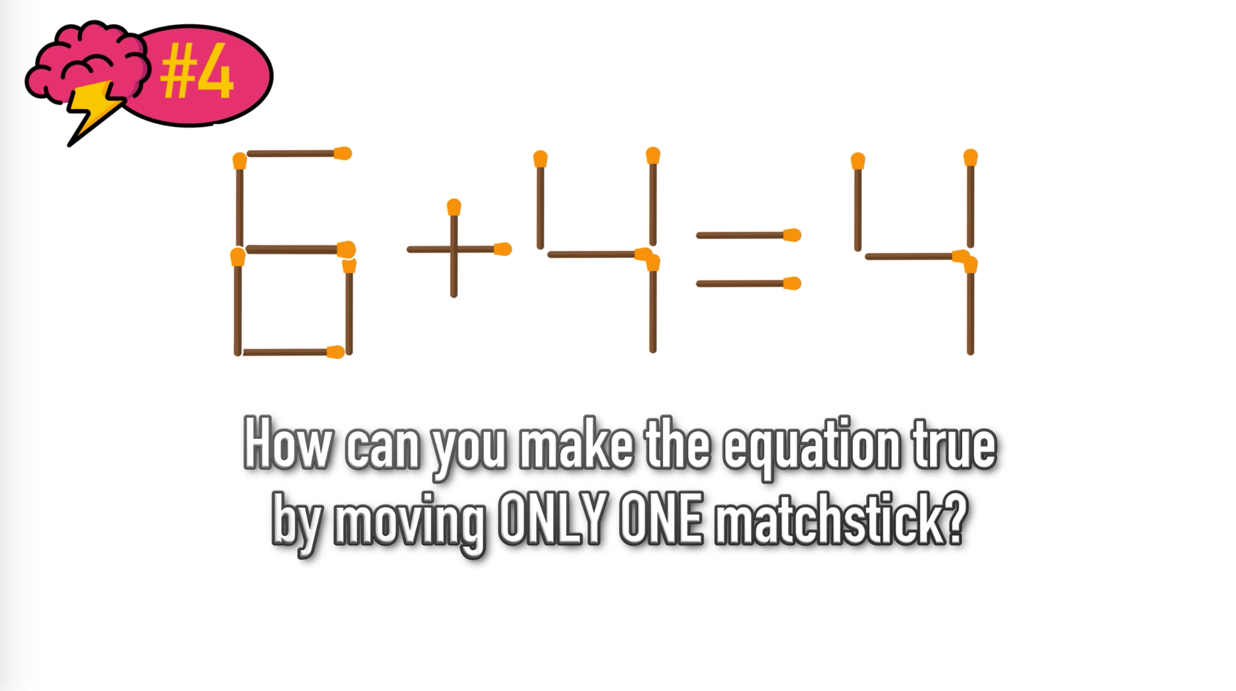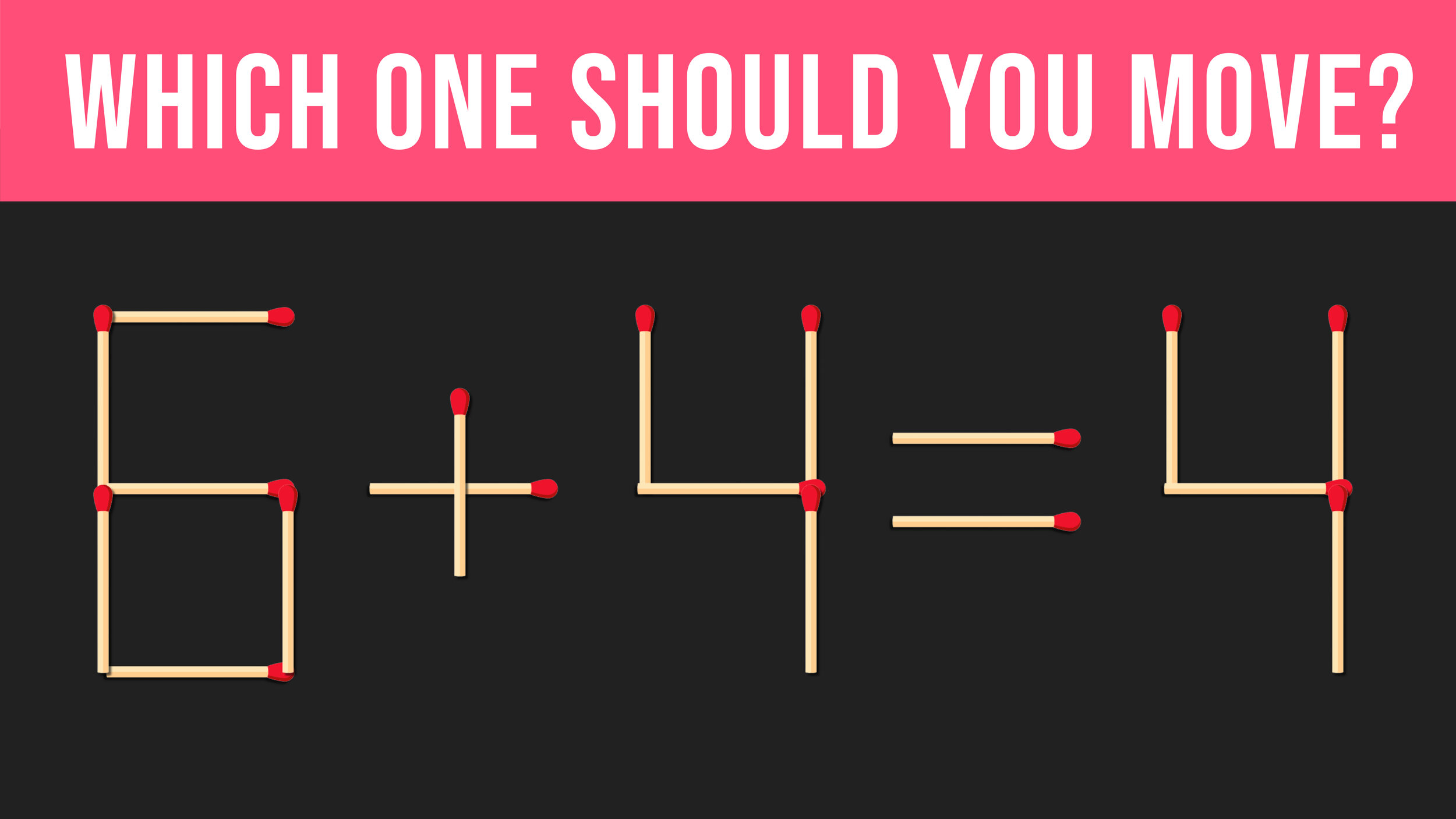10 Super Fun Math Riddles and Puzzles for Kids Ages 10+ (Answers Included!)
Some have been around for centuries, while are others are brand spanking new—but all have been selected as the most fun and engaging math riddles for those who love to challenge their problem-solving skills and have fun solving math puzzles. Enjoy!
The Educational Value of Math Riddles:
Fun and engaging math riddles and logic puzzles are an amazing way to get students to think critically, develop problem-solving skills, and think about mathematics in a creative way!
In fact, several recent studies have shown that students who work on math puzzles—with and without teacher supervision—improve their math problem-solving skills, learning abilities, and willingness to stick with challenging problems, according to Edutopia.
And if you are looking for a collection of super fun, challenging, and sometimes silly math riddles and brain teasers for kids, then it’s time to put your brain to the test!
Note that the following math riddles are best suited for kids ages and older and they are also fun for high school students and adults!
Are YOU ready?
There is also a link to download a Free Printable PDF Math Riddles Worksheet and Answer Key that shares all of these riddles at the end of this post!
All of the math riddles, puzzles, and brain teasers below are from the best-selling 101 Math Riddles, Puzzles, and Kids Ages 10+! PDF workbook, which is now available!
10 Awesome Maths Riddles and Brain Teasers for Kids:
Math Riddle #1: Truth or Square?
Keep reading to the bottom of this page to see the answer key AND click here to see a detailed explanation of how to solve Truth or Square?
Would you like FREE math resources in your inbox every day? Click here to sign up for my free math education email newsletter (and get a free math eBook too!)
Math Riddle #2: How Old Is Lucy?
Keep reading the bottom of this page to see the answer key AND click here to see a detailed explanation of how to solve How Old is Lucy?
Math Riddle #3: Triple Threat
Keep reading to the bottom of this page to see the answer key AND click here to see a detailed explanation of how to solve Triple Threat!
Are you looking for more super fun Math Riddles, Puzzles, and Brain Teasers to share with your kids?
The best-selling workbook 101 Math Riddles, Puzzles, and Brain Teasers for Kids Ages 10+! is now available as a PDF download. You can get yours today by clicking here.
Math Riddle #4: Matchstick Mayhem
Keep reading to the bottom of this page to see the answer key AND click here to see a detailed explanation of how to solve Matchstick Mayhem!
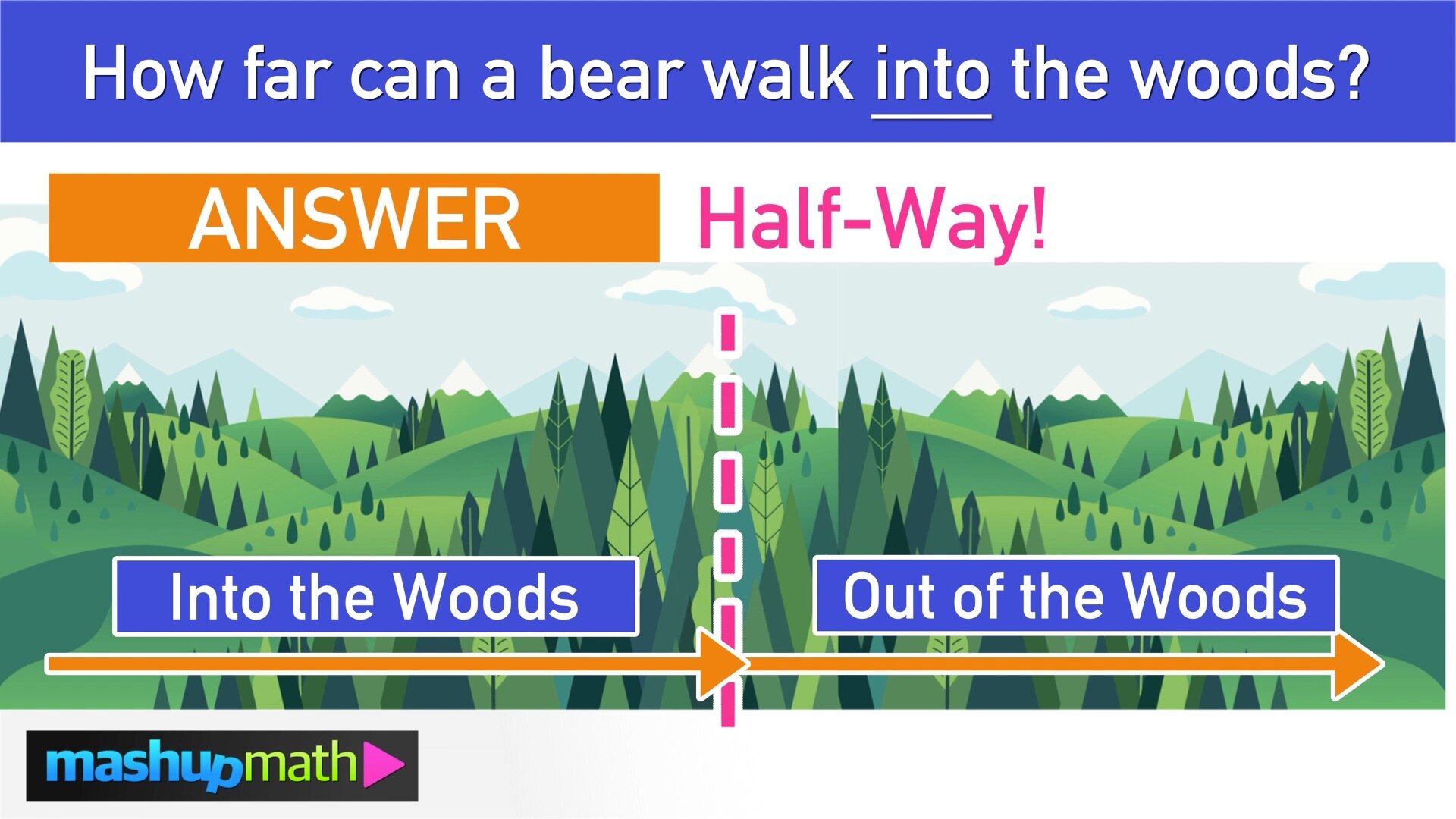
Math Riddle #5: The In-Between
Keep reading to the bottom of this page to see the answer key AND click here to see a detailed explanation of how to solve The In-Between!
Math Riddle #6: Which Weighs More?
Keep reading to the bottom of this page to see the answer key AND click here to see a detailed explanation of how to solve Which Weighs More?
Math Riddle #7: Big Spender!
Keep reading to the bottom of this page to see the answer key AND click here to see a detailed explanation of how to solve Big Spender!
Math Riddle #8: Mystery Parking!
Keep reading to the bottom of this page to see the answer key AND click here to see a detailed explanation of how to solve Mystery Parking!
Math Riddle #9: Cuppla’ Coins
Keep reading to the bottom of this page to see the answer key AND click here to see a detailed explanation of how to solve Cuppla’ Coins!
Math Riddle #10: Pascal’s Triangle
Keep reading to the bottom of this page to see the answer key AND click here to see a detailed explanation of how to solve Pascal’s Triangle!
Math Riddle #11: Bonus!
Keep reading to the bottom of this page to see the answer key AND click here to see a detailed explanation of how to solve the Bonus Riddle!
Looking for More Fun Math Riddles?
Check out our free collection of 36 Math Riddles for Kids (with answers)!
How many riddles can your kids solve?
ANSWER KEY:
14 Total Squares (detailed explanation)
Lucy is 37 (detailed explanation)
1, 2, and 3 (detailed explanation)
0+4=4 or 5+4=9 (detailed explanation)
A Decimal Point (detailed explanation)
Neither. They both weigh the same! (detailed explanation)
The hoodie costs $125, the shoes cost $25 (detailed explanation)
87 (flip the image upside down) - (detailed explanation)
One is a quarter and one is a nickel (detailed explanation)
1, 5, 10, 10, 5, 1 (detailed explanation)
Are you looking for more super fun Math Riddles, Puzzles, and Brain Teasers to share with your kids?
My best-selling workbook 101 Math Riddles, Puzzles, and Brain Teasers for Kids Ages 10+! is now available as a PDF download. You can get yours today by clicking here.
Did I miss your favorite math riddle for kids? Share your thoughts, questions, and suggestions in the comments section below!
(Never miss a Mashup Math blog--click here to get our weekly newsletter!)
By Anthony Persico
Anthony is the content crafter and head educator for YouTube's MashUp Math and an advisor to Amazon Education's 'With Math I Can' Campaign. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.