Performing Geometry Rotations: Your Complete Guide
The following step-by-step guide will show you how to perform geometry rotations of figures 90, 180, 270, and 360 degrees clockwise and counterclockwise and the definition of geometry rotations in math! (Free PDF Lesson Guide Included!)
Welcome to this free lesson guide that accompanies this Geometry Rotations Explained Video Tutorial where you will learn the answers to the following key questions and information:
What is the geometry rotation definition and what is the definition of rotation in math?
How to perform clockwise and counterclockwise rotations
How can you rotate a triangle about the origin?
Several geometry rotation examples
This Complete Guide to Geometry Rotations includes several examples, a step-by-step tutorial, a PDF lesson guide, and an animated video tutorial.
*This lesson guide accompanies our animated Geometry Transformations: Rotations Explained! video.
Want more free math lesson guides and videos? Subscribe to our channel for free!
Rotation Geometry Definition
Before you learn how to perform rotations, let’s quickly review the definition of rotations in math terms.
Rotation Geometry Definition: A rotation is a change in orientation based on the following possible rotations:
90 degrees clockwise rotation
90 degrees counterclockwise rotation
180 degree rotation
270 degrees clockwise rotation
270 degrees counterclockwise rotation
360 degree rotation
Note that a geometry rotation does not result in a change or size and is not the same as a reflection!
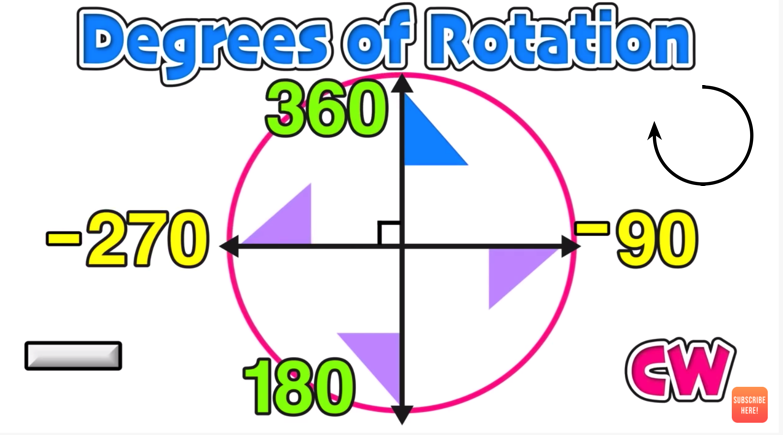
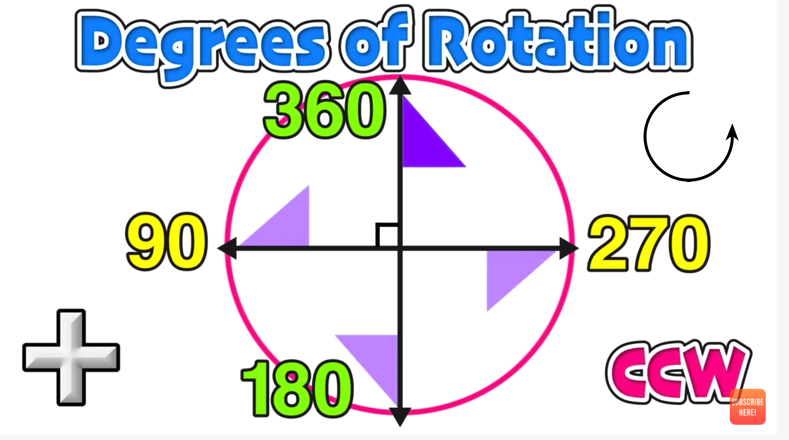
Clockwise vs. Counterclockwise Rotations
There are two different directions of rotations, clockwise and counterclockwise:
Clockwise Rotations (CW) follow the path of the hands of a clock. These rotations are denoted by negative numbers.
Counterclockwise Rotations (CCW) follow the path in the opposite direction of the hands of a clock. These rotations are denoted by positive numbers.
Clockwise rotations are denoted by negative numbers.
Counterclockwise rotations are denoted by positive numbers.
Note that the direction of rotation (CW or CCW) doesn’t matter for 180 and 360-degree rotations, since they will both bring you to the same spot (more on this later).
Geometry Rotation Notation
Note that the following notation is used to show what kind of rotation is being performed.
For example, Figure 1 is a rotation of -270 degrees (which is a CW rotation).
Figure 1
Now you are ready to try a few geometry rotation examples!
Geometry Counterclockwise Rotation Examples
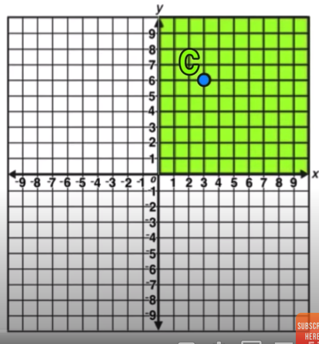
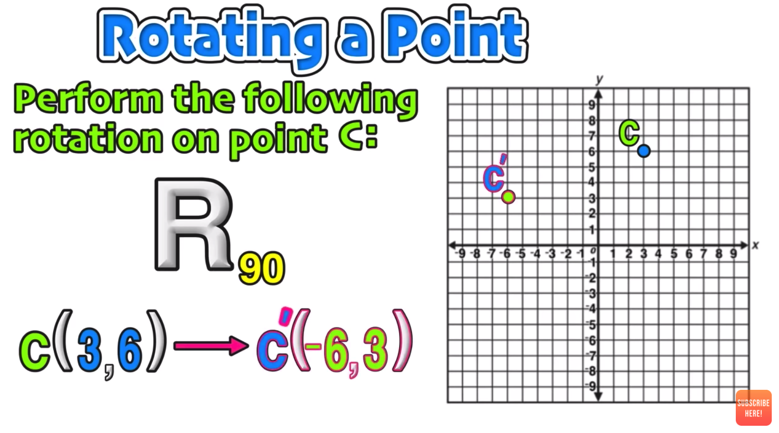
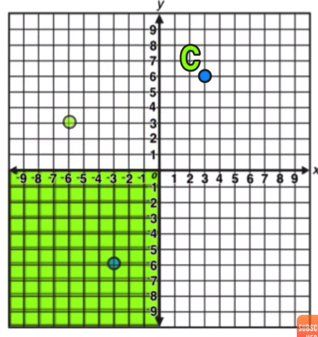
Example 01: 90 Degrees Counterclockwise About the Origin
Since 90 is positive, this will be a counterclockwise rotation.
In this example, you have to rotate Point C positive 90 degrees, which is a one quarter turn counterclockwise.
Point C lays in the 1st quadrant.
To perform the 90-degree counterclockwise rotation, imagine rotating the entire quadrant one-quarter turn in a counterclockwise direction.
Point C
Rotate the entire quadrant.
Plot point C’
Note the location of Point C’, the image of Point C after a 90-degree rotation.
And this process could be repeated if you wanted to rotation Point C 180 degrees or 270 degrees counterclockwise:
Point C after a 180-degree rotation.
Point C after a 270-degree rotation.
This example should help you to visually understand the concept of counterclockwise geometry rotations. Next, you will learn the rules for performing counterclockwise rotations.
>>> Before you move on, take some time to visualize what rotations look like on the coordinate plane.
<><><>
Counterclockwise Rotation Rules
You can use the following rules when performing any counterclockwise rotation.
By applying these rules to Point C (3,6) in the last example (Figure 2), you can see how applying the rule creates points that correspond with the graph!
Figure 2
These points should look familiar! They are the points that you plotted in the last example!
Geometry Clockwise Rotation Examples
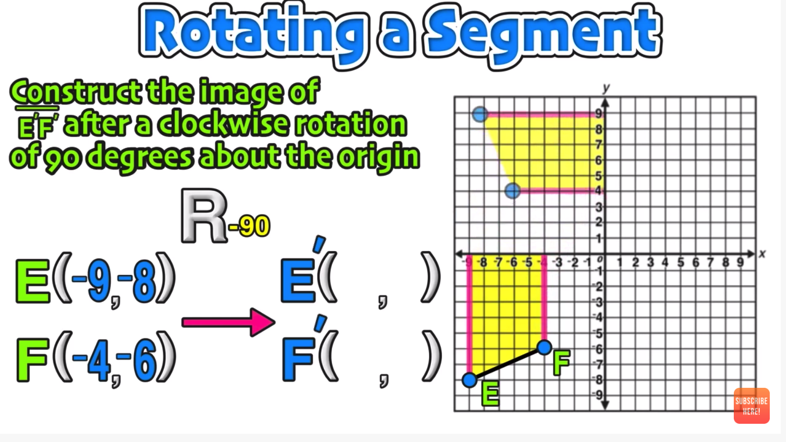
Example 01: 90 Degrees Clockwise About the Origin
Since the rotation is 90 degrees, you will be rotating the point in a clockwise direction.
Now imagine rotating the entire 4th quadrant one-quarter turn in a clockwise direction:
Point D
Rotate the entire quadrant
Plot Point D’
Note the location of Point D’, the image of Point D after a -90-degree rotation.
And this process could be repeated if you wanted to rotation Point D -180 degrees or -270 degrees counterclockwise:
Point D after -180 rotation
Point D after -270 rotation
This example should help you to visually understand the concept of clockwise geometry rotations. Next, you will learn the rules for performing clockwise rotations.
>>> Before you move on, take some time to visualize what rotations look like on the coordinate plane.
<><><>
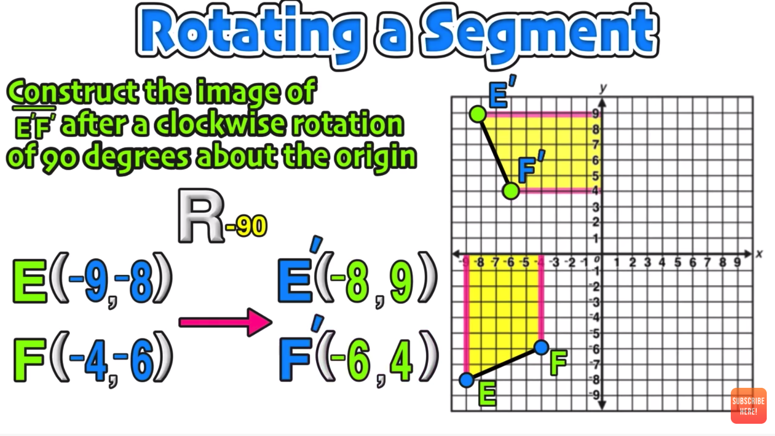
Clockwise Rotation Rules
You can use the following rules when performing any clockwise rotation.
By applying these rules to Point D (5,-8) in the last example (Figure 3), you can see how applying the rule creates points that correspond with the graph!
Figure 3
These points should look familiar! They are the points that you plotted in the last example!
More Geometry Rotations Examples
Example 01: Rotate a Line Segment 90 Degrees Clockwise
You can perform this rotation by using the rules or by doing a visual rotation as follows:
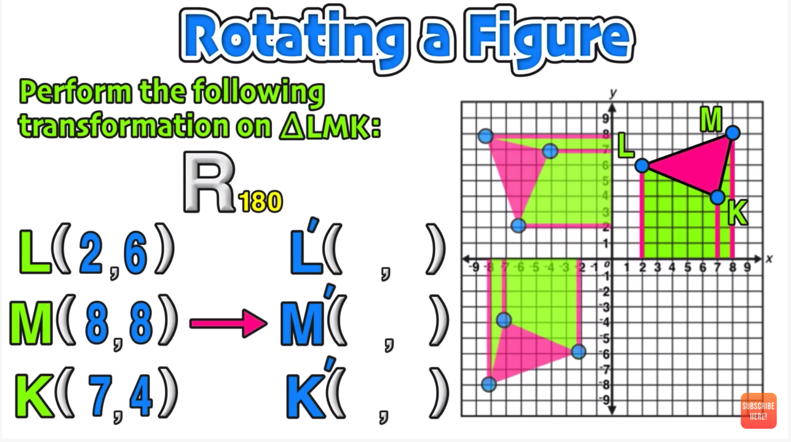
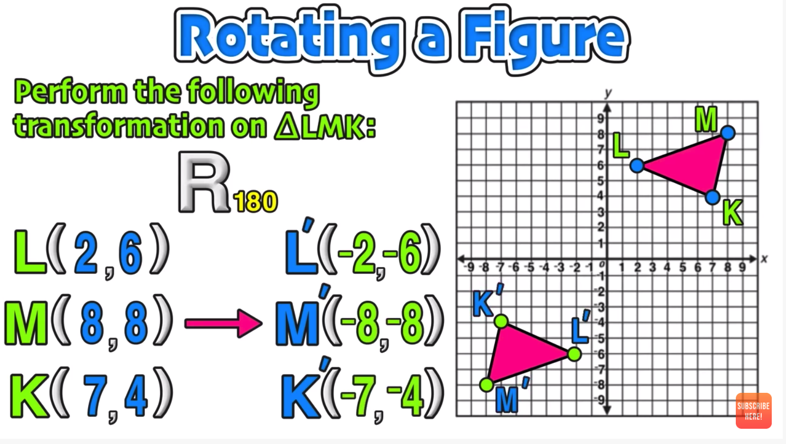
Example 02: Rotate a Triangle 180 Degrees
Note that it doesn’t matter which direction go (CW or CCW) for 180 degrees rotations, since you will end up in the same position either way!
You can perform this rotation by using the rules or by doing a visual rotation as follows:
Free Geometry Rotations Lesson Guide
Looking for more help with geometry rotations?
Click the link below to download your free PDF lesson guide that corresponds with the video lesson below!
Click here to download the Your Free PDF Lesson Guide
Still Confused?
Check out this animated video tutorial on geometry rotations:
Looking for more practice with Geometry Transformations?
Check out the following free resources:
Free Tutorial on Reflections!
Reflections Over the X- and Y-Axis: Complete Guide
Dilations and Scale Factor: Complete Guide
Keep Learning with More Free Lesson Guides:
Have thoughts? Share your thoughts in the comments section below!
(Never miss a Mashup Math blog--click here to get our weekly newsletter!)
By Anthony Persico
Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.