How to Find Perimeter in 3 Easy Steps

Math Skills: Learn how to find the perimeter of a rectangle, square, triangle, parallelogram, and circle.

Are you ready to learn how to find perimeter of various shapes and figures?

This free guide will teach you all about perimeter and how to find the perimeter of several common shapes. You can use the quick links below to jump to any section of this guide:

• Review: How to Find Perimeter

• Example: How to Find the Perimeter of a Square

• Example: How to Find the Perimeter of a Rectangle

• Example: How to Find the Perimeter of a Triangle

• Example: How to Find the Perimeter of a Parallelogram

• Example: How to Find the Perimeter of a Circle

In math, every student must learn how to find the perimeter of a two-dimensional shape. As long as you understand what perimeter means, you can easily find the perimeter of a shape by following a few easy steps.

For each example of how to find perimeter in this guide, we will use a simple 3-step method for finding perimeter that you can use to find the perimeter of any shape and to solve any math problem involving perimeter. As long as you can follow the three simple steps shared in this guide, you will always be able to find perimeter.

Let’s get started with a quick review of perimeter including some key vocabulary terms as well as an explanation of how to find perimeter before we move onto several specific examples.

How to Find Perimeter: Quick Review

Before you can learn how to find perimeter, you should be familiar with some important math concepts and vocabulary terms, which we will quick review here in this first section.

What is Perimeter?

Definition: In math, the perimeter of a shape is the total distance around the outer boundary of the shape.

Another way to describe the perimeter of a figure is the total measured length of the outline of the shape. Note that perimeter applies to two-dimensional shapes including triangles, rectangles, squares, etc.

For example, consider an equilateral triangle where each side has a length of 5 centimeters. To find the perimeter of the triangle, you would simply have to add up the lengths of all three sides as follows:

• 5 + 5 + 5 = 15 cm

Therefore, we could say that the triangle has a perimeter of 15 cm.

We can also think of perimeter as taking all of the side lengths of a shape and laying them out as one long straight line. The total length of this line would be the perimeter of the figure. This idea is illustrated in Figure 01 below.

On a larger scale, we can imagine a rectangular shaped park with a paved sidewalk surrounding it. The perimeter of the park would be the total distance that you would have to walk to travel the complete outer distance of the park (i.e. how far you would have to walk along the sidewalk to go around the park and end up back where you started.)

We can say that perimeter is the total distance around the outer boundary of a two-dimensional shape or figure.

Also, note that, unlike area, perimeter is only concerned with the outer boundary of a figure (not the inside of a figure).

Figure 02 below further illustrates the idea that the perimeter of a figure is the length of its outer boundary.

Now that you understand the concept of perimeter, you are ready to learn how to find a perimeter of several common two-dimensional shapes including squares, rectangles, triangles, parallelograms, and circles.

How to Find the Perimeter of a Square

Example #1: Find the Perimeter of a Square

For our first example, we have to find the perimeter of a square with a side length of 8m, as shown in Figure 03 below.

We can solve this first example of how to find the perimeter of a square (and all of the examples in this guide) by following the following three steps:

• Step #1: Identify the Shape

• Step #2: Identify all of the side lengths and add them together

• Step #3: Determine the perimeter and use appropriate units of measurement

Let’s go ahead and apply these three steps to this first example of how to find perimeter of a square.

Step #1: Identify the Shape

Our first step is super easy. We know that the figure in question is a square with four sides that all have the same length (8m in this case).

Step #2: Identify all of the side lengths and add them together

We know that each side of the square has a length of 8m, so we can add them together as follows:

• 8 + 8 + 8 + 8 = 32

Step #3: Determine the perimeter and use appropriate units of measurement

Finally, we can say that the length of the outer boundary of the figure is 32m and we can conclude that:

Final Answer: P=32m

Our procedure for solving this first example is illustrated in Figure 04 below.

That’s all that there is to finding perimeter! In this example, we learned how to find a perimeter of a square, but the steps that we used can be used to find the perimeter of any two-dimensional shape, as you will see in the following examples.

How to Find the Perimeter of a Rectangle

Example #2: Find the Perimeter of a Rectangle

In this next example, we will learn how to find the perimeter of a rectangle with a length of 12 ft and a width of 7 ft.

Just like the previous example, we can find the perimeter of this rectangle by using our three step strategy as follows:

Step #1: Identify the Shape

We already know that the shape in question is a rectangle that has four sides (two lengths and two widths). We also know that the opposite sides have equal measure, meaning that the two lengths equal 12 feet each and the two widths equal 7 feet each.

In many cases, all four sides of the figure will not be labeled, but you may find it helpful to go ahead and label them as shown in Figure 06 below:

Step #2: Identify all of the side lengths and add them together

Now that we have labeled all four side lengths, we can add them together as follows:

• 12 + 12 + 7 + 7 = 38

Step #3: Determine the perimeter and use appropriate units of measurement

And now, for the final step, we can say that the perimeter of the rectangle is 38 feet, and we can conclude that:

Final Answer: P=38 ft

The diagram in Figure 07 below summarizes how we found the perimeter of the rectangle in this example.

Now, let’s work through one more example of how to find perimeter of a rectangle.

Example #3: Find the Perimeter of a Rectangle

Notice that the rectangle whose perimeter we have to find in Figure 08 above has decimal side lengths.

This, however, will not change how we solve this problem and we can again use our three step strategy as follows:

Step #1: Identify the Shape

Since the shape in this example is a rectangle, we know that it has four sides, two of which have a length of 4.7 mm and two of which have a length of 8.1 mm.

Step #2: Identify all of the side lengths and add them together

Next, we can go ahead and find the sum of all four side lengths as follows:

• 4.7 + 4.7 + 8.1 + 8.1 = 25.6

Step #3: Determine the perimeter and use appropriate units of measurement

Now we can conclude that the rectangle has a perimeter of 25.6 mm.

Final Answer: P=25.6 mm

The diagram in Figure 09 below illustrates how we found the perimeter of a rectangle with a length of 4.7 and a width of 8.1.

How to Find the Perimeter of a Triangle

In this next section, we will focus on two examples of how to find the perimeter of a triangle. Unlike the last two sections where we focus on squares and rectangles, triangles only have three sides and they do not necessarily have right angles. However, these differences will not prevent us from finding the perimeter of a triangle using our three step strategy, as you will see in the examples below.

Example #4: Find the Perimeter of a Triangle

For this next example of how to find the perimeter of a triangle, we can again use our three step strategy to find the solution.

Step #1: Identify the Shape

In this example, we want to find the perimeter of a triangle (a three-sided shape). In this example, our triangle has side lengths of 30, 64, and 68.

Note that the triangle in this example, as shown in Figure 10 above, already has all three side lengths labeled for us.

Step #2: Identify all of the side lengths and add them together

For the second step, we have to add all three side lengths together as follows:

• 30 + 64 + 68 = 162

Step #3: Determine the perimeter and use appropriate units of measurement

Finally, we can say that the perimeter of the triangle is 162 units and we can conclude that:

Final Answer: P=162

The entire process for how to find the perimeter of a triangle is shown in Figure 11 below.

Example #5: Find the Perimeter of a Triangle

Here is another example of finding the perimeter of a triangle (in this case, a right triangle). Let’s go ahead and use our three step strategy to find the solution.

Step #1: Identify the Shape

Even though this example features a right triangle, we still know the side lengths to be 3.6, 4.8, and 6, so we have enough information to move onto the next step.

Step #2: Identify all of the side lengths and add them together

Now, we can find the sum of all three sides of the triangle as follows:

• 6 + 3.6 + 4.8 = 14.4

Step #3: Determine the perimeter and use appropriate units of measurement

From here, we know that the perimeter of the triangle is 14.4 units.

Final Answer: P=14.4

The steps for solving this problem on finding the perimeter of a triangle are in the diagram in Figure 13 below.

How to Find the Perimeter of a Parallelogram

Next, let’s take a look at an example of how to find the perimeter of a parallelogram.

Note that, in math, a parallelogram is a four-sided figure with two pairs of parallel sides where opposite sides are congruent in length. So, if you can find the perimeter of a rectangle or a square, then you can easily learn how to find the perimeter of a parallelogram.

Example #6: Find the Perimeter of a Parallelogram

Step #1: Identify the Shape

Notice that this example specifically asks us to find the perimeter of a parallelogram, so knowing the properties of parallelograms will be incredibly useful here (namely that the opposite sides of a parallelogram have congruent, or equal, lengths).

So, even though the parallelogram in the diagram shown in Figure 14 above only has two sides labeled, we actually have enough information to find the perimeter of the parallelogram.

Before we move onto the next step, let’s go ahead and label all four sides of the figure as shown in Figure 15 below.

Step #2: Identify all of the side lengths and add them together.

From here, we have a parallelogram with four side lengths: 40, 40, 54, and 54. For this second step to finding the perimeter of a parallelogram, we can find the sum of these four side lengths as follows:

• 40 + 40 + 54 + 54 = 188

Step #3: Determine the perimeter and use appropriate units of measurement

Now that we have found the sum of the four side lengths of the parallelogram, we can say that the perimeter equals 188 units.

Final Answer: P=188

The complete three step process of how to find the area of a parallelogram is illustrated in Figure 16 below.

Now that we have learned how to find the perimeter of a parallelogram, let’s move onto the final section of this guide on how to find the perimeter of shapes by looking at circles.

How to Find the Perimeter of a Circle

For this last section, we will focus on how to find a perimeter of a circle.

All of the shapes that we have previously covered in this guide (squares, rectangles, triangles, and parallelograms) had straight side lengths. However, circles do not have any sides at all, so how can we possibly find the perimeter of a circle?

Remember that the concept of perimeter refers to the length of the outer boundary of a figure. And, when it comes to circles, the term that refers to its outer boundary is called its circumference.

So, anytime you are wondering how to find the perimeter of a circle, you should really be wondering how to find the circumference of that circle!

And, to find the circumference of a circle, we will have to use the circumference of a circle formula:

• C=πd

In other words, the perimeter of a circle (i.e. the circumference of a circle) is equal to the product of π and its diameter.

With this in mind, let’s work through two examples of how to find the perimeter of a circle using the circumference formula.

*Note that in the examples below, we will use a calculator to make calculations using the exact value for π. However, you can approximate by as 3.14 to find estimated answers if you do not have access to a calculator will a π button.

Example #7: Find the Perimeter of a Circle

In the case of finding the perimeter of a circle, our three step strategy will not work.

In fact, you will rarely see questions that ask you to find the perimeter of a circle. Rather, they will more often require you to find the circumference of the circle, which is exactly what we will do to solve this problem.

Again, we will be using the formula C=πd where d is the length of the circle’s diameter, which, in this example, is 116 inches.

So, we can use the formula as follows:

• C = π x d

• C = π x 116

• C = 364.424747…

• C ≈ 364.4

For this example, we will round our answer to the nearest tenth and we can conclude that the perimeter of the circle is 364.4 inches.

Final Answer: P = 364.4 inches

Now, let’s move onto our very last perimeter example where you will gain more practice with how to find a perimeter of a circle.

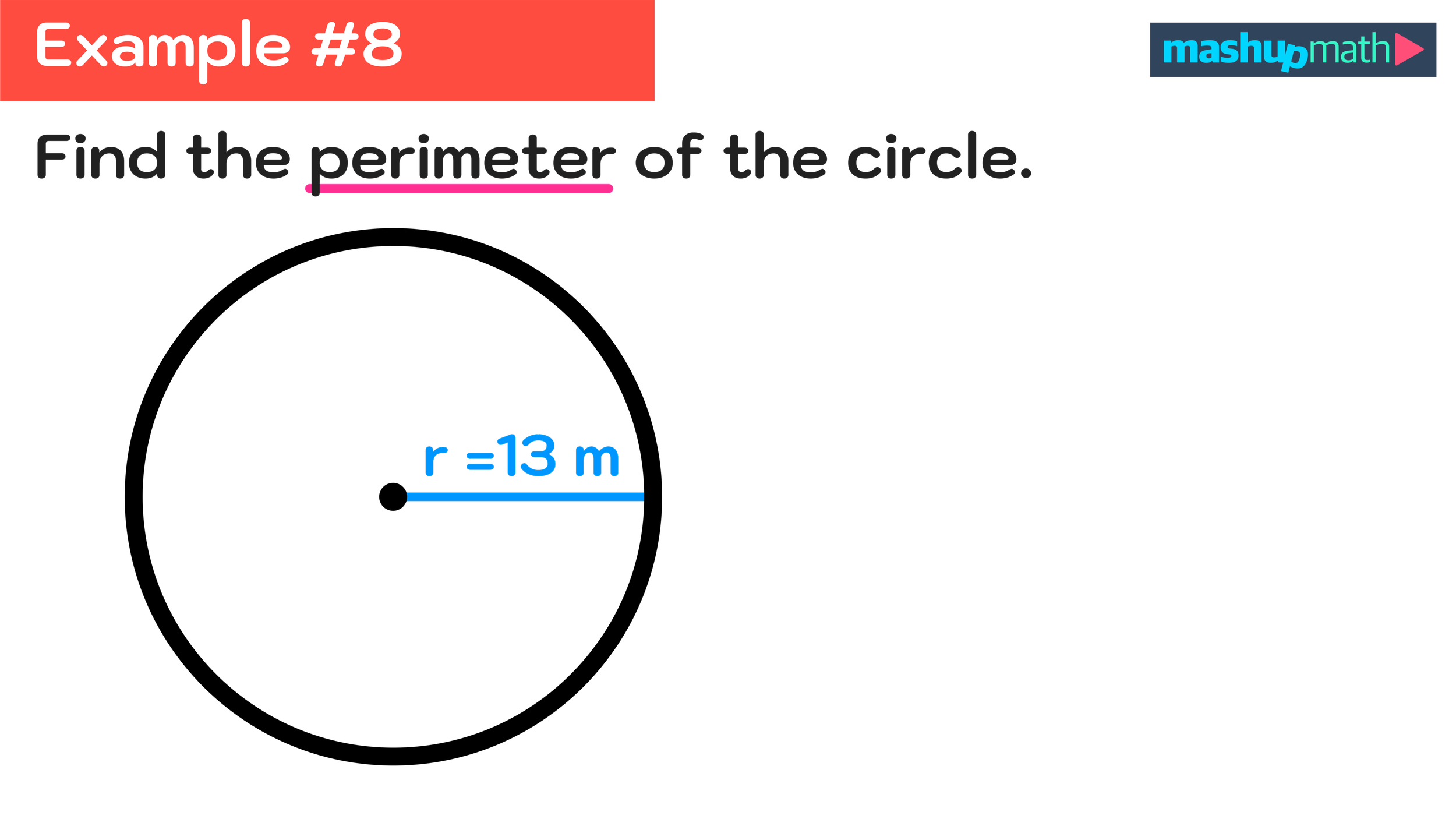
Example #8: Find the Perimeter of a Circle

We can solve this example of finding the perimeter of a circle the same way that we did the previously one.

However, notice that this example only gives us the length of the circle’s radius and not its diameter.

To find the length of the radius, we simply have to double the length of the given radius (13 m) as follows:

• d = r x 2

• d = 13 x 2

• d = 26

Now that we know that the circle has a radius of 26m, we can use the circumference of a circle formula to find its perimeter as follows:

• C = π x d

• C = π x 26

• C = 81.6814089…

• C ≈ 81.7

Rounding our answer to the nearest tenth, we can conclude that the circle has a perimeter of approximately 81.7.

Final Answer: P = 81.7 m.

Conclusion: How to Find Perimeter

In math, the perimeter of a shape is the total distance around the outer boundary of the shape. You can also think of perimeter as the measured distance along the outline of the shape.

In this guide on how to find perimeter, we worked through several examples of how to find the perimeter of a rectangle, a square, a triangle, and a parallelogram using the following three step strategy:

• Step #1: Identify the Shape

• Step #2: Identify all of the side lengths and add them together

• Step #3: Determine the perimeter and use appropriate units of measurement

We also looked at the special case of how to find the perimeter of a circle, where we used the circumference formula, C = π x d, the find the length of the outer boundary of any circle.

Finding the perimeter of a shape is a relatively easy math skill that you can learn through practice and understanding the meaning of perimeter and the procedure for finding it will help you to solve problems inside and outside of the math classroom.

Keep Learning

How to Find the Area of a Parallelogram in 3 Easy Steps

Learn how to find the area of any parallelogram in this free step-by-step guide.

Search Tags: how to subtract fractions, subtracting fractions, how to subtract fractions with different denominators, fraction subtraction, subtracting fractions with unlike denominators, how do you subtract fractions?