How to Find the Circumference of a Circle

Step-by-Step Guide: What is the circumference of a circle? How to find the circumference of a circle using the formula for circumference of a circle?

Understanding how to find the circumference of a circle is an important math skill that every student must learn.

In order to learn how to find the circumference of a circle, you need to be familiar with the concept of circumference and how to use the formula for circumference of a circle to solve problems where you are tasked with finding the length of a circle’s circumference.

This free Step-by-Step Guide on How to Find the Circumference of a Circle will teach you how to use the circle formula, C=πd, to find circumference of a circle. The guide is organized by the following sections/subtopics:

What is the Circumference of a Circle?
Circumference of a Circle Formula
How to Find the Circumference a Circle with Diameter
How to Find the Circumference of a Circle with Radius

While we recommend that you work through in section in order, you can use the links above to jump to any section of interest.

Are you ready to get started? Let’s begin with a review of some important properties of circles that you will need to be familiar with in order to learn how to find the circumference of a circle.

What is the Circumference of a Circle?

Before we get into what the circumference of a circle actually means, there are some key circle-related vocabulary terms that you should be familiar with:

A circle’s diameter is any line that passes through the center point of the circle and touches two points on the edge of the circle.
A circle’s radius is any line segment that runs from the center point and touches the edge of the circle.
A radius of a circle, r, will always be equal to half the length of its diameter, d. In other words, r=2d.
Conversely, the diameter of a circle, d, will always be equal to twice the length of its radius, r. In other words, d=2r.

These key properties of circles are illustrated in Figure 01 above for your reference. Make sure that you understand them well before moving on.

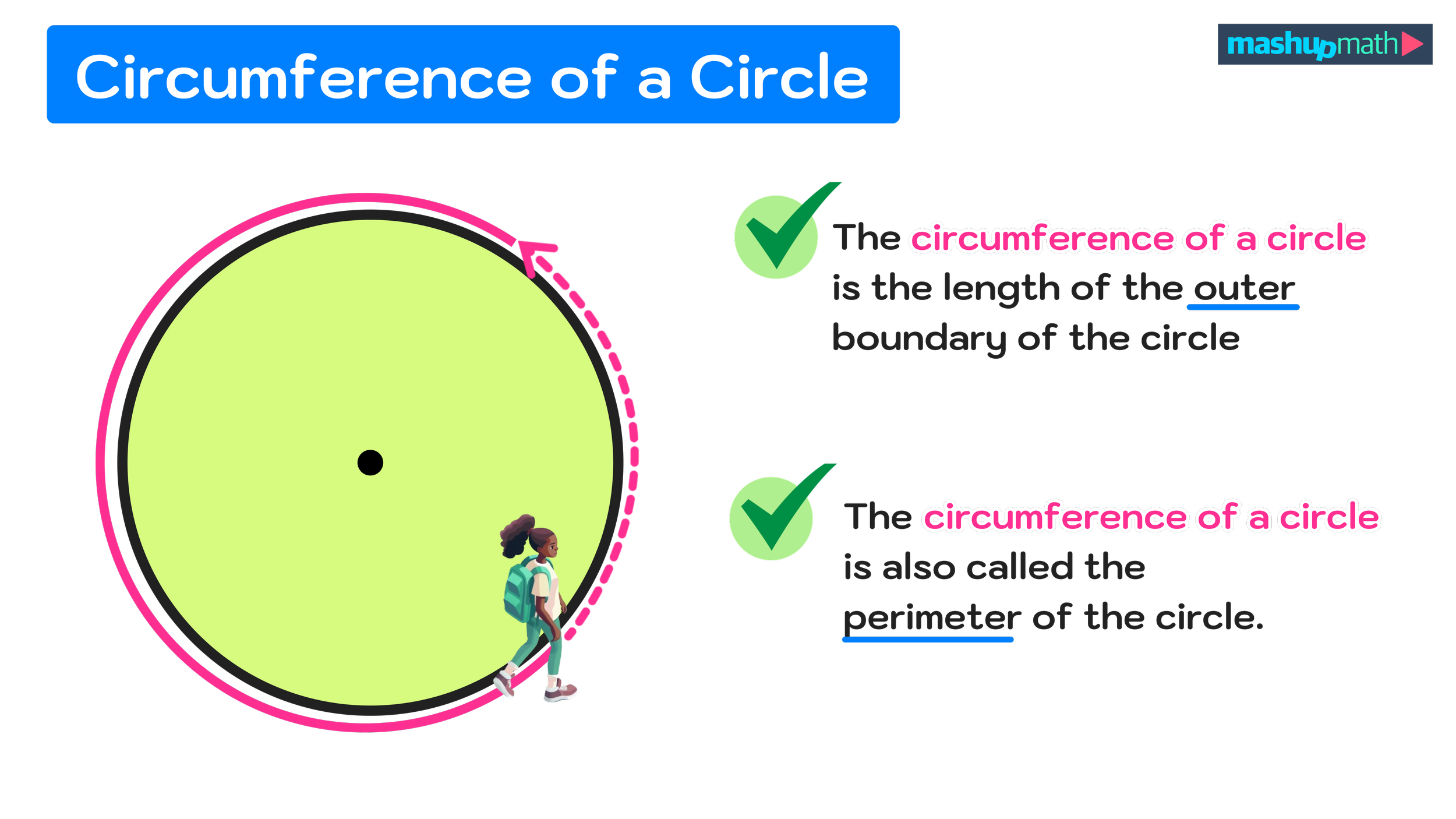
What is the circumference of a circle?

The circumference of a circle is the length of its outer boundary. The circumference of a circle is sometimes referred to as a perimeter of a circle and it is always measured in units such as inches, centimeters, yards, etc.

In real-world terms, you could find the circumference of a circle by taking the outer boundary of a circle and flattening it out into a straight line and then measuring the length of that straight line. Whatever the length is would be the circumference of the circle.

For example, if you have a section of rope that was 4 feet long and you curled it into a perfect circle, the circle will also have a circumference of 4 feet, as shown in Figure 02 below.

The biggest takeaway here is that the circumference of a circle is the total length of the outer region of the circle. You could imagine taking a circle, cutting it somewhere, and then bending it so it forms a straight line. You could then find the circumference by measuring that straight line.

The diagram in Figure 03 below further illustrates the concept of circumference in mathematical terms.

Now that you understand what the circumference of a circle represents, let’s move onto the next section, where will we learn the circumference of a circle formula.

Circumference of a Circle Formula: C=πd

You can find the circumference of any circle simply by using the circumference of a circle formula: C=πd (where d is the length of the diameter of the circle).

In other words, circumference equals pi times diameter.

Whenever you are using the circumference of a circle formula, you have the option of using pi (π) or an approximation of pi (π≈3.14). If you have a calculator that has a π button, we highly recommend using it instead of approximating pi as 3.14, since it will give you more accurate answers. However, both options are acceptable in most cases.

Before continuing onto the next section, be sure to remember that the d in the circumference formula represents the length of the circle’s diameter. You can use the diagram in Figure 04 below as a reference for remembering that the circumference of a circle formula is C=πd.

For example, let’s say that we wanted to find the circumference of a circle with a diameter of 10 cm. Knowing that d=10 in this example, we could solve this problem by using the circumference of a circle formula as follows:

C=πd and d=10
C=π(10) or C=10π
C=31.41592654…
C=31.4 cm

So, we can conclude that the circle has an approximate circumference of 31.4 centimeters. We figured this out by substituting d with 10 in the formula to get C=π(10) or C=10π (this both mean the same thing—the product of 10 and π) and using our calculator to get C=31.41592654…, which we rounded to the nearest tenth decimal place to get C=31.4 cm.

Note that we will be expressing circumference to the nearest tenth of decimal place for all of the examples in this guide.

The step-by-step process for finding the circumference of a circle with a diameter of 10cm is shown in Figure 05 below.

Now that you know how to use the circumference formula, you are ready to learn how to find the circumference of a circle by working through a several examples.

How to Find Circumference of a Circle with Diameter

In the previous section, we learned how to find the circumference of a circle with diameter of 10cm. The step-by-step process for solving thing problem is illustrated in Figure 05 above.

As long as you know that the circle circumference formula is C=πd, you can solve any problem where you have to find the circumference of a circle with diameter given. To do this, simply substitute d with the numerical value of the length of the diameter and then multiply it by π to determine the length of the circle’s circumference.

This method is exactly how we will solve our first practice problem. Let’s go ahead and get started.

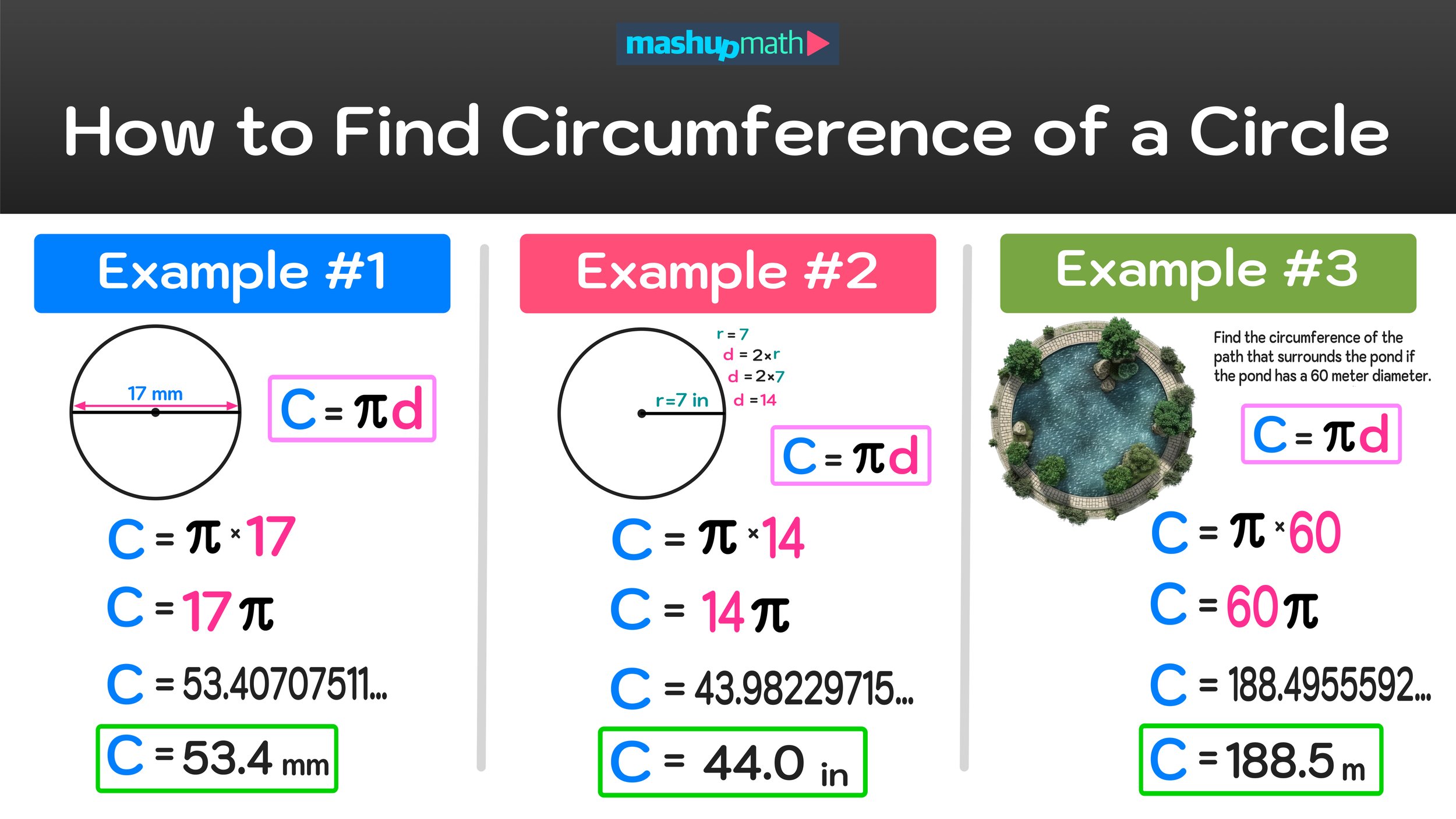
Example #1: Find the Circumference of a Circle with Diameter 17 mm

For this first example, we have to find the circumference of a circle with diameter of 17 mm.

We can solve this problem by using the circumference of a circle formula, C=πd, by inputting d=17 into the formula and solving as follows:

C=πd
C=π(17) pr C=17π

C=53.40707511…
C=54.4 mm

Final Answer: The circle has a circumference of 54.4 mm.

Finished! As long as you know the length of a circle’s diameter, you can input it into the circle circumference formula to calculate its circumference.

The step-by-step process for solving Example #1 are shown in Figure 06 below. Be sure that you are comfortable with this process before moving onto the next example.

Example #2: Find the Circumference of a Circle with Diameter 20.6 yd

For this next example, we want to calculate the circumference of a circle with diameter 20.6 yd.

Notice that the value of the diameter, d, in this example is a decimal. However, you can still use the formula, C=πd, to solve this problem and find the circumference of the circle as follows:

C=πd
C=π(20.6) or C=20.6π

C=64.71680866…
C=64.7 yd

Final Answer: The circle has a circumference of 64.7 yd.

This process for using the circumference of a circle formula to find the circumference of a circle with a diameter of 20.6 yd is illustrated in Figure 06 below.

Now, let’s work through one more example of how to find circumference of a circle with diameter in a real-world context.

Example #3: Find the Circumference of a Circle with Diameter 60 meters

For this third example, we want to find the circumference of a paved sidewalk that surrounds a circular pond with a diameter that is 60 meters long.

Even though this is a real-world scenario, we can still use the circumference formula to find the answer as follows:

C=πd
C=π(60) or C=60π

C=188.4955592…
C=188.5 m

Final Answer: The paved sidewalk has a circumference of 188.5 meters.

The diagram in Figure 07 illustrates this real-world scenario and how we used our formula to figure out the circumference of the path that surrounds the circular pond.

How to Find Circumference of a Circle with Radius

You probably have learned that finding the circumference of a circle when you are given the length of its diameter is a pretty straightforward process, but what happens when only know the length of the circle’s radius and not the length of its diameter?

As long as you understand the relationship between a circle’s radius and its diameter, you can easily use a given radius to figure out the length of the diameter. And this skill is extremely useful because it will allow you to use the circumference of a circle formula, C=πd, to solve circle problems where only the radius is given.

Recall from our vocabulary review at the start of this guide that a radius of a circle is any line segment that starts at the center and ends on the edge of the circle and that the radius of a circle is equal to half the length of the circle’s diameter.

r = d/2

Conversely, we can say that the diameter of a circle is equal to twice the length of its radius:

d=2r

So, if you know the length of the radius of a circle, you can use it to find the length of the diameter, d, by multiplying it by 2.

For example, if you were given a circle with a radius of 5 feet (r=5). You could take the radius and double it to find the value of the diameter, which, in this case, would be 10 ft.

r=5
d=2r
d=2(5)
d=10

The diagram in Figure 08 below illustrates this relationship between the radius and the diameter of a circle.

The key takeaway is that the diameter of a circle is equal to twice the length of its radius.

Now, let’s go ahead and apply our understanding of this relationship to another practice problem.

Example #4: Find the Circumference of a Circle with Radius of 7 inches

In this example, we have to find the circumference of a circle with a radius of 7 inches (r=7).

Our goal is to solve this problem the same way that we solved the three previous examples where we calculated circumference using the formula C=πd.

However, the difference between Example #4 and the previous three is that, in this case, we are given the radius of the circle, r, and not the diameter.

But we can use the given radius, r=7, to find the length of the diameter, d, because we know that the diameter of a circle is equal to twice the length of its radius:

d=2r
d=2(7)
d=14

Therefore, if the circle has a radius of 7 inches, then it also has a diameter of 14 inches (because 7x2=14).

Now that we know the value of d (d=14 in this case), we can substitute it into the circumference of a circle formula and solve as follows:

C=πd
C=π(14) or C=14π

C=43.98229715
C=44.0 in

Final Answer: The circle has a circumference of 44 inches.

The entire step-by-step process for solving this fourth and final example are illustrated in Figure 09 below. If you are still confused about how to find the circumference of a circle, we recommend that you go back and work through the practice problems again.

How to Find the Circumference of a Circle: Conclusion

The circumference of a circle, also known as its perimeter, is the length of its outer boundary.

Understanding how to find the circumference of a circle is a foundational math skill that has many practical applications both inside and outside of the math classroom.

Whenever you have to find the circumference of a circle, you can use the formula C=πd, where d represents the lengths of the circle’s diameter, to find an answer.

If you are given the length of the circle’s diameter, you can substitute it for d in the formula and solve. However, if you only know the circle’s radius, you will have to multiply it by two (d=2r) to find the length of its diameter, d, before you can use the formula.

However, as long as you know the circumference of a circle formula and the relationship between the radius and diameter of a circle, you can easily calculate the circumference of a circle in just a few simple steps.