How to Round to the Nearest Thousandth—Step-by-Step Guide

How to Round to the Nearest Thousandth

Rounding to the Nearest Thousandth in 3 Easy Steps

Free Step-by-Step Guide: How to round to the nearest thousandth.

Learning how to correctly round numbers, especially numbers with decimals, is an important math skill that will help you to work with numbers, make accurate estimations, and solve problems.

Many students find rounding to be a relatively easy skill to learn when it comes to working with whole numbers, but many of those same students will struggle with rounding once decimals are involved. However, while rounding decimal numbers may seem trickier than rounding whole numbers, the process remains the same and learning how to round to the nearest thousandth decimal place is a math skill that every student can easily learn.

Ready to learn how to round to the nearest thousandth? This free step-by-step guide will show you how to round to the nearest thousandth by working through six different practice problems together. By working through each problem together, you will gradually learn everything you need to know about rounding to the nearest thousandth to the point that you will be able to solve decimal rounding problems with ease.

For this guide on rounding, you can work through each section in order, or you can use the quick links below to jump to a particular section of interest:

• What is Rounding?

• Rounding Up vs. Rounding Down

• How to round to the nearest thousandth in 3 simple steps?

• Rounding to the Nearest Thousandth Examples

(Looking for help with rounding to the nearest tenth and rounding to the nearest hundredth?)

What is Rounding?

In math, the process of rounding involves taking a given number and rewriting it as a new number that serves as a close estimation of its actual value. Why? Because, mathematically speaking, doing so makes the original number easier to work with.

Consider a smoothie that costs $7.95. By rounding to the nearest whole number (or whole dollar in this case), you could say that the cost of a smoothie is $8. If you had to figure out the cost of 13 smoothies, without rounding, you would have to calculate 7.95 x 13 = ?, which isn’t exactly the easiest multiplication problem to solve in your head. On the other hand, if had to figure out the cost of 13 smoothies after rounding $7.95 to $8, you can determine close estimate of the actual cost simply by performing 8 x 13 = $104. So, you could say that the approximate cos of 13 smoothies would be $104.

• Actual Cost: 7.95 x 13 = $103.35

• Estimated Cost: 8.00 x 13 = $104.00

Notice how rounding made this problem much easier to solve and the difference between the actual cost and the estimated cost is relatively small.

The key takeaway here is that rounding a mathematical tool that you can use to estimate values and make them easier to work with and perform operations on.

Figure 01: The process of rounding involves taking a given number and rewriting it as a new number that serves as a close estimation of its actual value

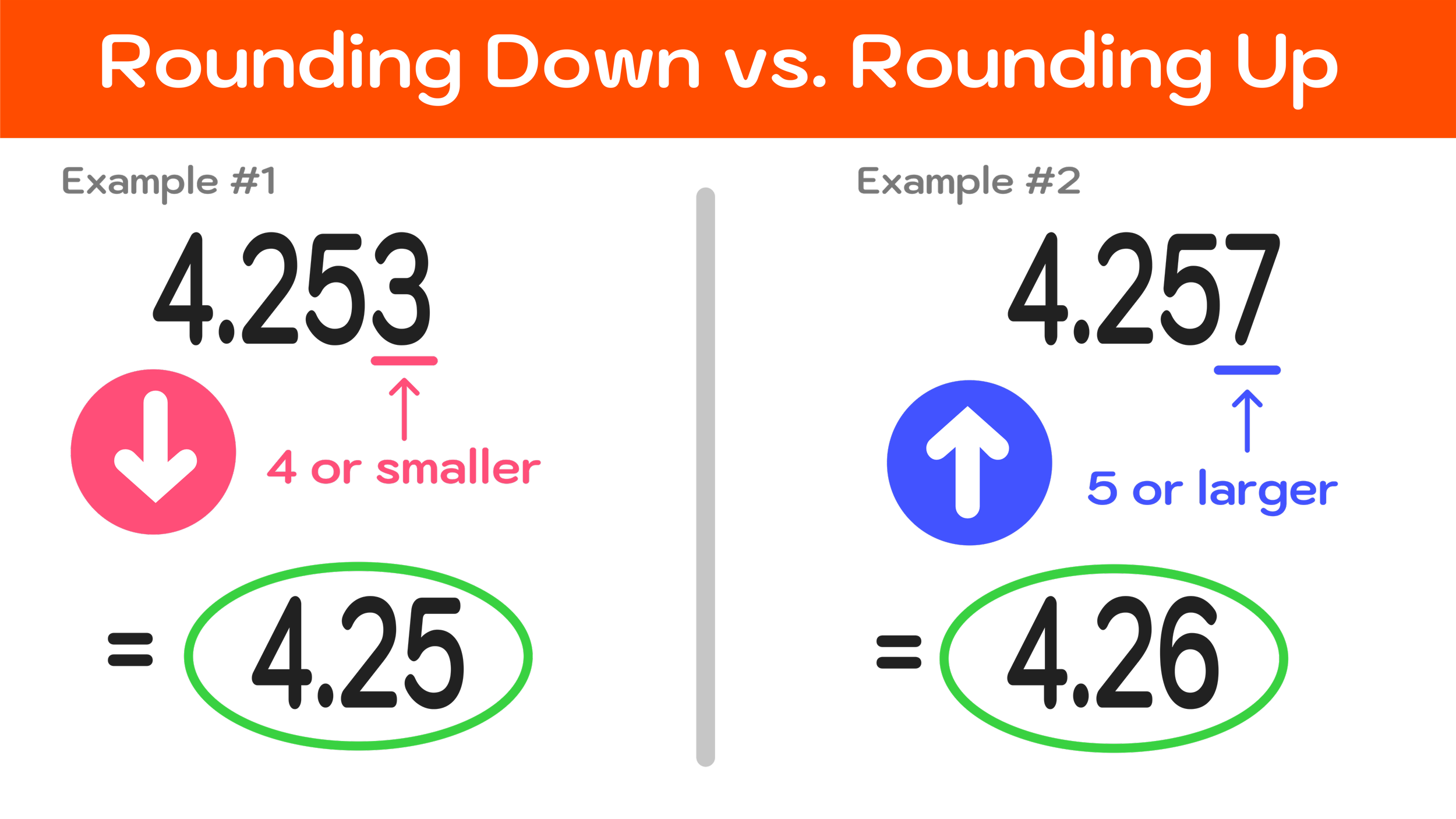
Rounding Up vs. Rounding Down

Next, let’s run through a quick refresher on the difference between rounding up and rounding down.

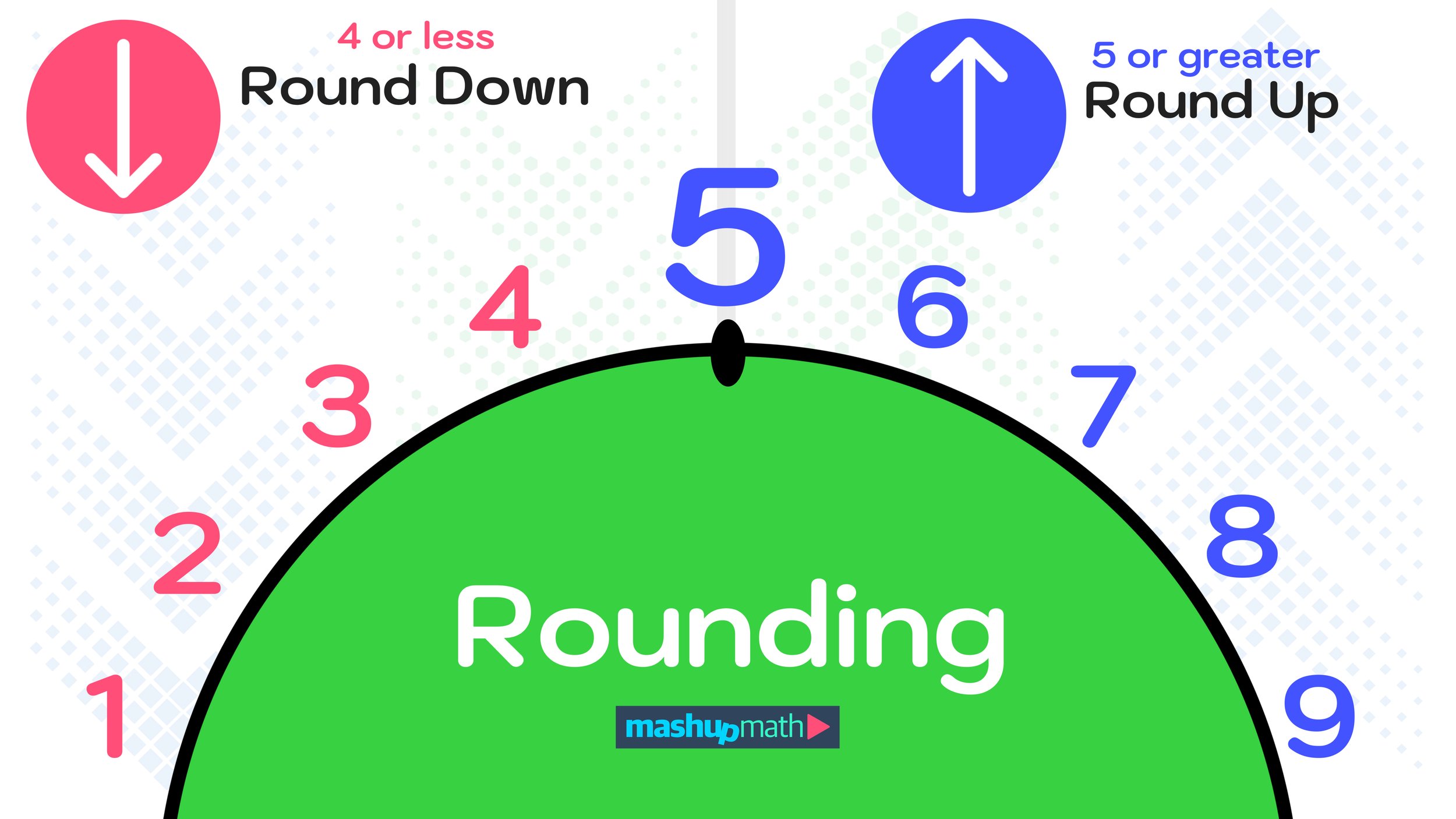
You probably already know that, when it comes to rounding, the number 5 is a big deal. Why?

Rounding Rule: If the number directly to the right of the number you are rounding is greater than or equal to 5, then you will round up. Conversely, if the number directly to the right of the number you are rounding is less than or equal to 4, then you will round down.

As far as rounding rules go, this is the only true definition that you will need to remember if you want to learn how to successful round to the nearest thousandth. And, this rule will apply to any rounding problem you will come across, so make sure that you have a firm understanding of it before moving on.

Reminder:

• If the number directly to the right of the number you are rounding is ≥ 5 → round up

• If the number directly to the right of the number you are rounding is ≤ 4 → round down

Let’s consider two simple examples:

Example A: Round 128 to the nearest ten.

In this example, 2 is in the tens decimal place and the number 8 is directly to the right of it. Since 8 ≥ 5, you will have to round up the 2 as follows:

• 128 → 130

Example B: Round 254 to the nearest ten.

In this example, 5 is in the tens decimal place and the number 4 is directly to the right of it. Since 4 ≤ 4, you will have to round down the 5 as follows:

• 254 → 250

Figure 02: Whenever the number directly to the right of the number you are rounding is ≥ 5, you have to round up. Otherwise, round down.

3-Step Process: How to Round to the Nearest Thousandth

Now that you understand what it means to round a number and the difference between rounding up and rounding down, you are ready to learn how to round to the nearest thousandth and work through some practice problems.

For all of the rounding to the nearest thousandth examples in this guide, we will be using the following 3-step process for rounding to the nearest thousandth:

• Step #1: Locate and underline the value in the thousandths place value slot

• Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

• Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

It’s ok if this 3-step process seems complicated at first glance. After working through a few examples, you will become much more comfortable with using these three steps to solve decimal rounding problems with ease

---

Example #1: Round to the Nearest Thousandth: 5.3641

Let’s go ahead and dive into our first example where we are tasked with rounding 5.3641 to the nearest thousandth.

We will solve this problem (and all of the practice problems in this guide) using the previously described 3-step process as follows:

Step #1: Locate and underline the value in the thousandths place value slot

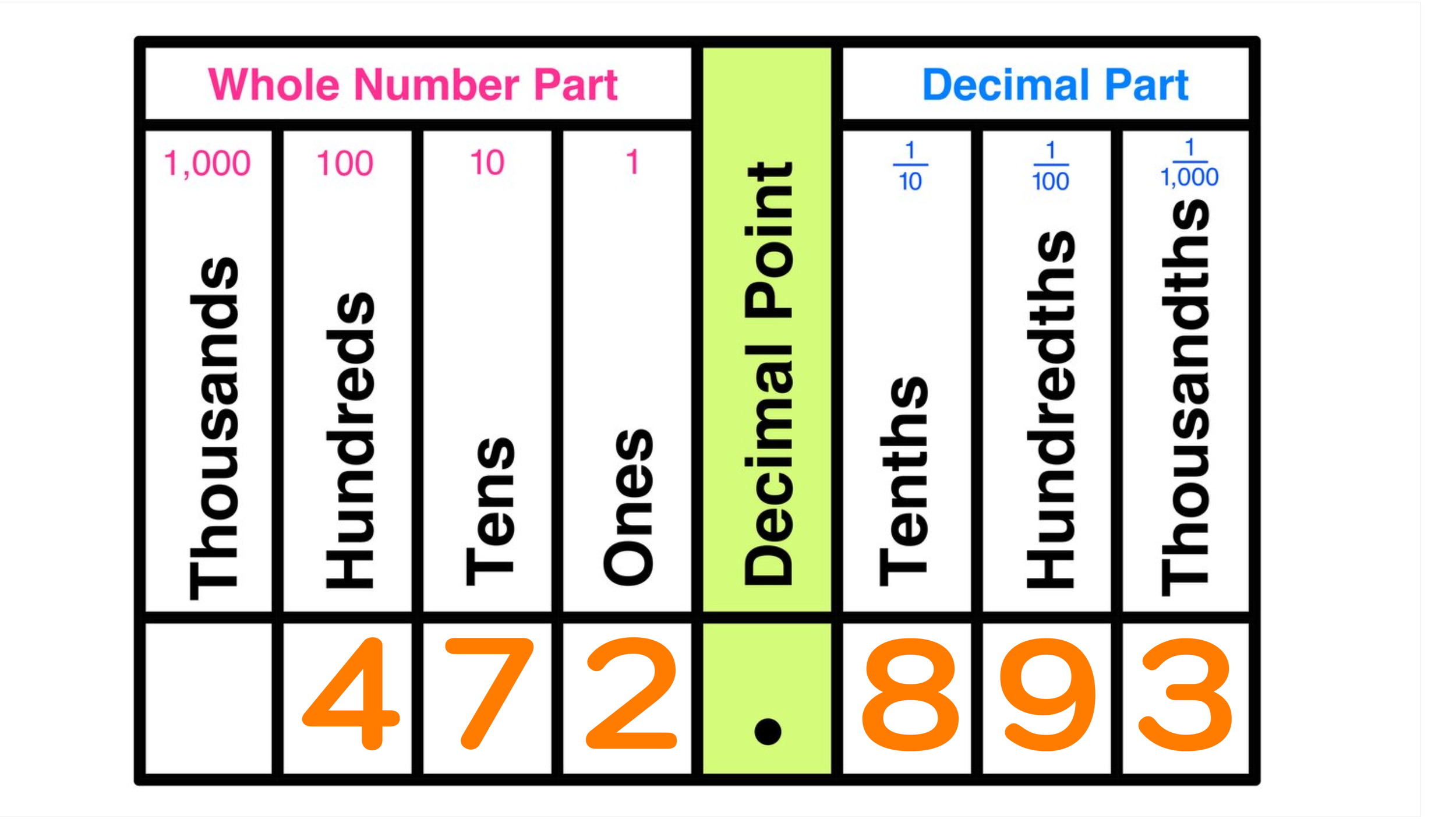
For the number 5.3641, there are four numbers to the right of the decimal place. The third number to the right of the decimal place will always be the thousandths place value slot, which, in this example, is the number 4.

Locating and underlining the value in the thousandths place vale slot is illustrated in Figure 03 below.

Figure 03: How to round to the nearest thousandth: The first step is to identify the thousandths place value slot.

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

Next, take a look at the number directly to the right of the 4 in the thousandths place value slot.

In this example, that number is 1, which is ≤ 4.

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

Since the number directly to the right of the 4 in the thousandths place value slot is 1, which is ≤ 4, you will have to round down.

In this case, rounding down means that the 1 to the right of the 4 in the thousandths place value slot becomes a zero and effectively disappears, which leaves us with:

Final Answer: 5.3641 rounded to the nearest thousandth is 5.364

The complete process of solving this first example is shown in Figure 04 below:

Figure 04: When rounding down, the number to the right of the thousandths decimal slot becomes a zero and disappears.

---

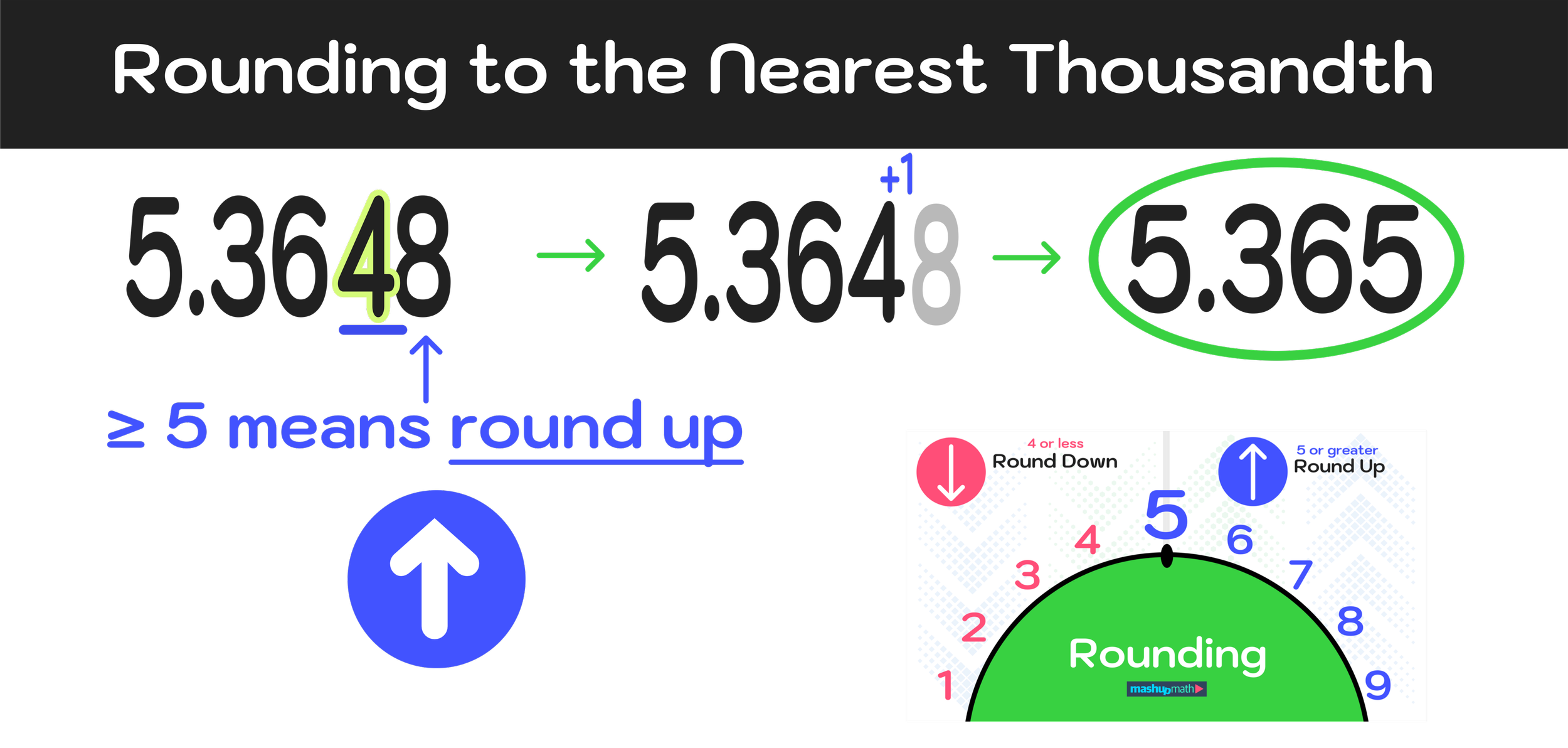
Example #2: Round to the Nearest Thousandth: 5.3648

For the next example, you will notice that the number in question is very similar to the previous example. In this case, the only difference is that the final number is an 8 rather than a 1.

How will this difference effect the final answer? Let’s apply our 3-step process and see:

Step #1: Locate and underline the value in the thousandths place value slot

For this example, the number 4 is in the thousandths place value slot as shown in Figure 05 below.

Figure 05: How to round to the nearest thousandth: Start by identifying the value in the thousandths decimal slot.

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

In this example, the number directly to the right of the 4 in the thousandths place value slot is 8.

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

The number directly to the right of the 4 in the thousandths place value slot is 8, and 8≥ 5, so this time we will be rounding up.

When rounding up, you will add one to the value in the thousandths place value slot (4 in this example) and all numbers to the right of it will disappear.

Final Answer: 5.3648 rounded to the nearest thousandth is 5.365

This process of solving Example #2 is illustrated in Figure 06 below.

Figure 06: 5.3648 rounded to the nearest thousandth is 5.365

Before moving onto more practice problems, let’s take a closer look at the differences between rounding the numbers in Example #1 and Example #2 to the nearest thousandth:

• Example #1: 5.3641 → 5.364 (we rounded down)

• Example #2: 5.3648 → 5.365 (we rounded up)

The graphic in Figure 07 below further highlights the differences between how we solved these first two examples (namely, the difference between solving by rounding down and solving by rounding up).

Figure 07: Examples of rounding down vs. rounding up.

---

Example #3: Round to the Nearest Thousandth: 1.27025

Moving onto this next example, you will notice that the number 1.27025 includes five digits to the right of the decimal point. However, whenever you are rounding to the nearest thousandth, you will only need to first four digits and anything beyond that can be ignored.

To see this process in action, let’s go ahead and apply our 3-step process for rounding to the nearest thousandth.

Step #1: Locate and underline the value in the thousandths place value slot

For the number 1.27025, the number 0 is in the thousandths place value slot, as shown in Figure 08 below.

Figure 08: Remember that you only need the first four digits the right of the decimal point to round a number to the nearest thousandth. Anything beyond that can be ignored.

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

Next, notice that 0 is in the thousandths place value slot and the number directly to the right of it is a 2, which is ≤ 4.

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

Since 2 ≤ 4, we will be rounding down to solve this problem as is shown in Figure 09 below:

Final Answer: 1.27025 rounded to the nearest thousandth is 1.270

Figure 09: 1.27025 rounded to the nearest thousandth is 1.270

---

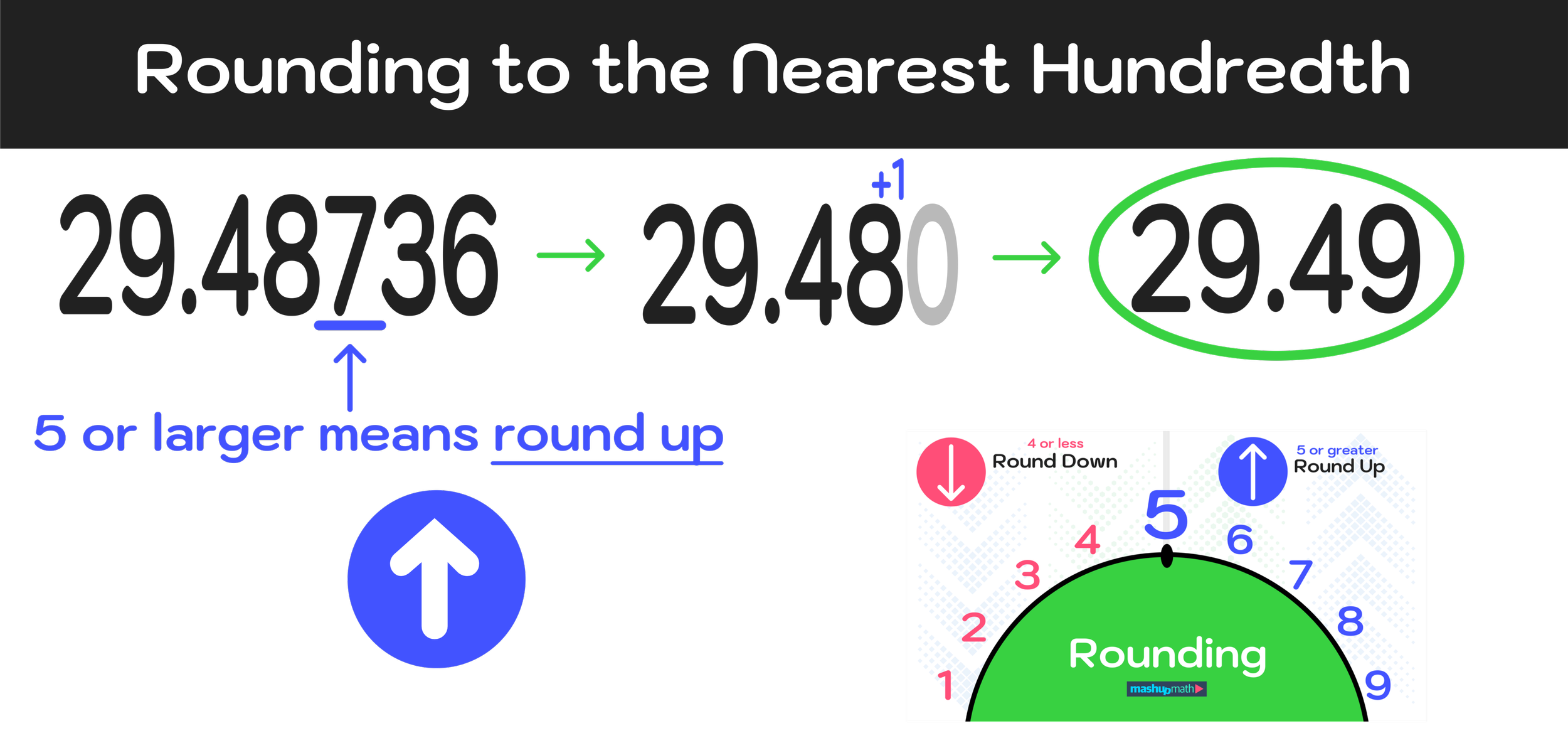
Example #4: Round to the Nearest Thousandth: 24.3759414

Again, we can solve this problem by applying our 3-step process. Just remember that you can ignore any numbers that come after the fourth number to the right of the decimal point.

Step #1: Locate and underline the value in the thousandths place value slot

For the number 24.3759414, the number 5 is in the thousandths place value slot.

Figure 10: The number 5 is in the thousandths place value slot.

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

The number directly to the right of the 5 is 9, and 9 ≥ 5.

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

Since 9 ≥ 5, you must round it up to solve this problem and conclude that:

Final Answer: 24.3759414 rounded to the nearest thousandth is 24.376

Figure 11 below illustrates the entire 3-step process for rounding Example #4 to the nearest thousandth.

Figure 11: 24.3759414 rounded to the nearest thousandth is 24.376

---

Example #5: Round to the Nearest Thousandth: 18.34951

Are you starting to get the hang of it? Let’s continue onto another example.

Step #1: Locate and underline the value in the thousandths place value slot

For the number 18.34951, the digit in the thousandths place value slot is 9.

Figure 14: How to Round to the nearest Thousandth: The digit in the thousandths place value slot is 9.

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

Next, the number directly to the right is 5, and 5 ≥ 5.

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

Since 5 ≥ 5, we know that we have to take the 9 in the thousandths place value slot and round it up. But how do you round up the number 9 without turning it into a 10?

Rule: Whenever you are rounding up the number 9, you have to turn it into a zero and add one to the number directly to the left of the 9.

Figure 13 below illustrates the application of this rule being used to solve Example #5.

Final Answer: 18.34951 rounded to the nearest thousandth equals 18.350

Figure 13: Whenever you are rounding up the number 9, you have to turn it into a zero and add one to the number directly to the left of the 9.

---

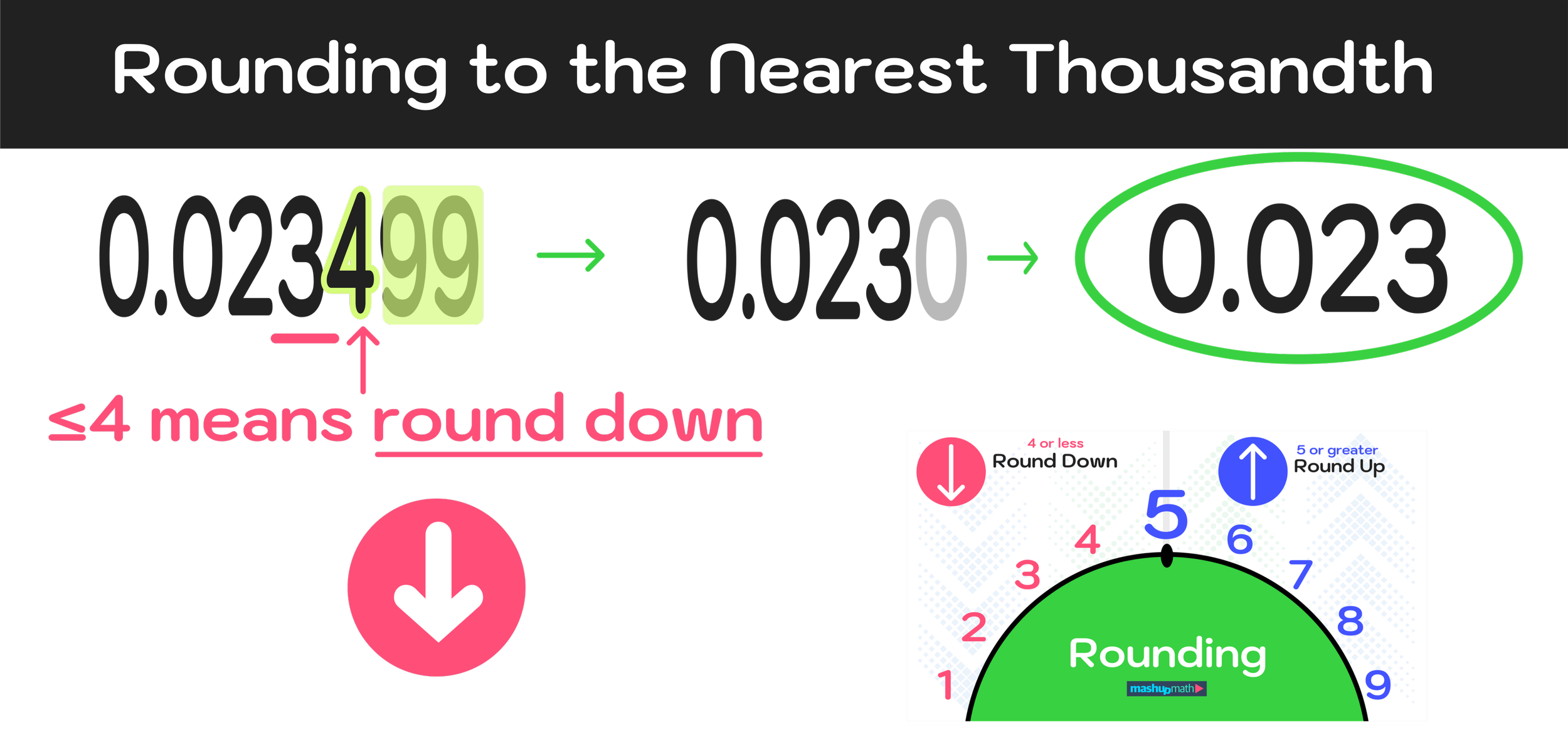
Example #6: Round to the Nearest Thousandth: 0.023499

You made it to the final example! To solve this last problem, we will again rely on our 3-step process as follows:

Step #1: Locate and underline the value in the thousandths place value slot

In this example, 0.023499, the number 3 is in the thousandths place value slot.

Figure 14: Reminder: When it comes to rounding to the nearest thousandth, you can ignore any additional numbers after the fourth digit to the right of the decimal point.

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

Notice that the number directly to the right of the 3 is a 4.

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

Since 4 ≤ 4, we know that we have to round down to solve this problem.

Final Answer: 0.023499 rounded to the nearest thousandth is 0.023

Figure 15: Rounding 0.023499 to the nearest thousandth.

---

Conclusion: Round to the Nearest Thousandth

Rounding numbers, especially decimals, is an extremely important and useful math skill that helps students to estimate numbers and make calculations with them.

This guide specifically focused on rounding to the nearest thousandth, where you learned and applied a simple 3-step method to rounding any number to the nearest thousandth decimal place:

Step #1: Locate and underline the value in the thousandths place value slot

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

You can use this 3-step process to solve any problem where you have to round a given number to the nearest thousandth! So, it should be no surprise that we were able to use it to solve all six practice problems in this guide and make the following conclusions:

• 5.3641 → 5.364

• 5.3648 → 5.365

• 1.27025 → 1.270

• 24.3759414 → 24.376

• 18.34951 → 18.350

• 0.023499 → 0.023

Need some extra practice? If so, we strongly recommend that you go back and work through the practice problems in this guide again. The more that you practice, the more comfortable you will become with the 3-step process. And, if you need some additional practice beyond this guide, check out the free rounding worksheets and answer keys available on our free math worksheet libraries.

Keep Learning:

How to Round to the Nearest Hundredth (Step-by-Step Guide)

Continue your rounding journey by learning how to round to the nearest hundredth.

---

How to Round to the Nearest Hundredth—Step-by-Step Guide

How to Round to the Nearest Hundredth

Step-by-Step Guide: Rounding to the Nearest Hundredth in 3 Easy Steps

Free Step-by-Step Guide: How to round to the nearest hundredth.

Knowing how to round numbers, especially numbers involving decimals, is an incredibly useful math skill that will help you to work large and small numbers and estimate their values.

While rounding whole numbers can be relatively straightforward, the process gets a little trickier when decimals are involved. However, this guide will make sure that you are familiar with key vocabulary and our easy-to-follow three-step method for rounding numbers to the nearest hundredth. Once you learn to apply this method, you can use it to solve any problem where you are tasked with rounding to the nearest hundredth.

Are you ready to get started? The following free guide will teach you everything you need to know about rounding to the nearest hundredth including step-by-step explanations of solving several practice problems.

While we highly recommend that you read each section in order, you can use the quick links below to jump to a specific topic or section:

• What does rounding a number mean?

• What does rounding to the nearest hundred mean in terms of place value?

• How to round to the nearest hundred in 3 simple steps?

• Examples of rounding to the nearest hundredth

(Looking for help with rounding to the nearest tenth and rounding to the nearest thousandth?)

What does rounding a number mean?

Rounding a number is the process of rewriting a number to a value that closely estimates its actual value so that is easier to understand and perform operations on.

For example, if a large coffee costs $4.97, you could estimate the cost to be $5 even (this would be an example of rounding to the nearest whole number). If someone asked you how much money you would need to purchase six coffees, you could easily estimate the cost to be $30 (since 5 x 6 =30), rather than having to figure out the value of 4.97 x 6.

So, rounding is just a method of making larger or small numbers easier to work with.

Figure 01: An example of rounding is estimating that the cost of a $4.97 cup of coffee to be $5 since it is an easier number to work with.

When do you round down and when do you round up?

Now that you understand what rounding means, it is important that you know the difference between situations when you have to round up and when you have to round down.

In the case of rounding, the number 5 is extremely significant.

RULE: If the number to the right of the number you are rounding is 5 or greater, then you must round up. If the number to the right of the number you are rounding is 4 or less, then you must round down.

This rule applies to rounding any whole number or decimal number. To help you to remember this rule, you can use the “rounding hill” shown in Figure 02 below to help you remember when to round up and when to round down.

• If digit to the right of the number being rounded is 4 or less → round down

• If digit to the right of the number being rounded is 5 or greater → round up

For example, if you wanted to round 58 to the nearest ten, the rounded answer is 60 since 8 (the number to the right of the tens digit) is 5 or greater, meaning you have to round up.

• 58 → 8 is 5 or greater, so round up → 60

On the other hand, if you wanted to round 43 to the nearest ten, the result would be 40 since 3 (the number to the right of the tens digit) is 4 or less, meaning you have to round down.

• 43 → 3 is 4 or less, so round down → 40

Figure 02: This illustration of a “rounding hill” can help you to remember when to round up and when to round down.

What does rounding to the nearest hundredth mean in terms of place value?

The last key topic that we have to review before we start working on some examples of rounding to the nearest hundredth is place value.

Definition: Place Value is the numerical value that a digit has based on its position in the number.

Consider the number 472.893

We can think of the number 472.893 as the sum of:

• 4 hundreds

• 7 tens

• 2 ones

• 8 tenths

• 9 hundredths

• 3 thousandths

Just like the “rounding hill” in Figure 02, you can use a place value chart, as shown in Figure 03 below, as a visual tool to help you to correctly identify the place values of digits in any given number.

▶ FREE DOWNLOAD: Blank Decimal Place Value Chart (PDF File)

Before moving forward, make sure that you have a strong understanding of place value and that you can correctly identify place values, especially for values to the right of a decimal sign.

Figure 03: You can use a place value chart to help you to correctly identify the place value of each digit in a number.

Keep Learning: Where is the hundredths place value in math?

Since this guide focuses on rounding to the nearest hundredth, here are a few examples of identifying the hundredths and thousandths place value digit for the following numbers.

• 5.279 → 7 is in the hundredths decimal place, 9 is in the thousandths decimal place

• 76.105 → 0 is in the hundredths decimal place, 5 is in the thousandths decimal place

• 0.444 → 4 is in the hundredths decimal place, 4 is in the thousandths decimal place

• 2,000.018 → 1 is in the hundredths decimal place, 8 is in the thousandths decimal place

Figure 04: How to identify the hundredths and thousandths decimal places in a given number.

How to Round to the Nearest Hundredth using 3 Simple Steps

Ready to work through some practice problems focused on rounding to the nearest hundredth?

For all of the practice problems in this guide, you can use the following 3-step process for rounding to the nearest hundredth:

• Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

• Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

• Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

If these three steps seam confusing at first, that’s okay. They will make more sense once you get some experience applying them to the following practice problems.

---

Example #1: Round to the Nearest Hundredth: 4.253

Starting off with our first example, we are tasked with rounding the number 4.253 to the nearest hundredth.

We can solve this problem by applying the 3-step method as follows:

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

For the number 4.253, the 3 is in the thousandths decimal place slot (and there are no additional numbers to the right of it).

Figure 05: For the number 4.253, the number 3 is in the thousandths place value slot.

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

For this example, 3 is in the thousandths place value slot and 3 is 4 or smaller, so we will have to round down in the third and final step.

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

In the last step, we determined that the value in the thousandths place value slot, 3, is 4 or smaller and that we have to round down. When rounding down, we turn that 3 in the thousandths place value slot into a zero, which effectively makes it disappear. Now, we can conclude that:

Final Answer: 4.254 rounded to the nearest hundredth is 4.25

The final answer to Example 1 (and the steps to solving it) is displayed in Figure 06 below.

Figure 06: When rounding down, the number in the thousandths decimal spot becomes a zero and disappears.

---

Example #2: Round to the Nearest Hundredth: 4.257

Notice that Example #2 is very similar to Example #1. The only difference is that, in this example, the value of the number in the thousandths place value slot is a 7 (rather than a 3).

Let’s go ahead and apply our 3-step method to see how this difference affects our answer.

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

For the number 4.257, the 7 is in the hundredths place value slot as illustrated in Figure 07 below.

Figure 07: The thousandths place value slot is three digits to the right of the decimal point.

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

As previously stated, for this example, the value of the number in the thousandths place value slot is a 7, which is 5 or larger.

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

Since the value in the thousandths place value slot is 5 or larger, we have to round up to solve this problem. When rounding up, we have to add one to number in the tenths place value slot (the number directly to the left of the number in the thousandths place value slot) and “zero out” the number in the thousandths place value slot.

Final Answer: 4.257 rounded to the nearest hundredth is 4.26

The entire process of solving this second example is illustrated in Figure 08 below.

Figure 08: 4.257 rounded to the nearest thousandth is 4.26.

Before we move onto more practice problems, Figure 09 below compares the first two examples. Be sure that you understand the difference between rounding up and rounding down before moving on.

Figure 09: Comparing Example #1 (rounding down) and Example #2 (rounding up). What do you notice?

---

Example #3: Round to the Nearest Hundredth: 88.7309

For this third example, notice that there is a digit in the ten-thousandths decimal place (the value four digits to the right of the decimal point). While this number, 88.7309 is larger than the numbers in the first two examples, you can still use the 3-step method for rounding to the nearest hundredth to solve it.

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

For the number 88.7309, the thousandths place value digit (the number three digits to the right of the decimal point) is 0. Remember that you can ignore any numbers to the right of the digit in the thousandths place value slot (which is the 9 in this example).

For the sake of rounding correctly, you can ignore the 9 and think of this number as 88.730.

Figure 10: Remember that you can ignore any numbers to the right of the digit in the thousandths place value slot.

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

Next, notice that 0 is in the thousandths place value slot. Clearly, 0 is 4 or smaller.

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

Since 0 is 4 or smaller, we will have to round down. Since 0 is already 0, we can just make it disappear and make the following conclusion:

Final Answer: 88.7309 rounded to the nearest hundredth is 88.73

This final answer is shown in Figure 11 below.

Figure 11: 88.7309 rounded to the nearest hundredth is 88.73.

---

Example #4: Round to the Nearest Hundredth: 29.48736

Similar to the previous example, 29.48736 includes numbers the right of the thousandths decimal place. Remember that you can ignore these numbers and use the three steps to solve this problem as follows:

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

For the number 29.48736, the number 7 is in the thousandths place value slot.

Figure 12: When rounding to the nearest hundredth, the number in the thousandths place value slot will determine if you have to round up or down.

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

Since 7, the number in the thousandths place value slot, is 5 or larger, we will have to round up in step three.

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

To round this number to the nearest hundredth, you must add one to the 8 in the tenths place value slot and zero out the 7.

Final Answer: 29.48736 rounded to the nearest hundredth is 29.49

The complete three-step process for solving example #5 is shown in Figure 13 below.

Figure 13: 90.352 rounded to the nearest tenth is equal to 90.4

---

Example #5: Round to the Nearest Hundredth: 8.495

By now, you should be a bit more comfortable with rounding to the nearest hundredth. Let’s continue on to work through two more examples where we will gain more experience using the 3-step method.

For this next example, we have to round the number 8.495 to the nearest hundredth.

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

For the number 9.495, the digit in the thousandths place value slot is 5, as shown in Figure 14 below.

Figure 14: How to Round to the nearest Hundredth: When the digit in the thousandths place value slot is 5 or larger, you have to round up.

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

Next, we can see that 5 (digit in the thousandths place value slot) is indeed 5 or larger.

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

Since 5 is 5 or larger, we will have to round up. The number directly to the left of the thousandths digit is a 9, so how do we round it up without turning it into a double-digit number? In the case of rounding up the number 9, you must turn it into a zero and add one to the number directly to its left (this process is illustrated in Figure 15 below).

Final Answer: 8.495 rounded to the nearest hundredth equals 8.50

Figure 15: 8.495 rounded to the nearest hundredth equals 8.50

---

Example #6: Round to the Nearest Hundredth: 64.01408

Here is our final practice problem for rounding to the nearest hundredth!

To solve it, let’s go ahead and apply our 3-step method as follows:

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

For this last problem, the digit in the thousandths place value slot is 4, as shown below in Figure 16. Remember that all of the digits to the right of the 4 can be ignored.

Figure 16: Remember that, when it comes to rounding to the nearest tenth, you can ignore any additional numbers that come after the digit in the thousandths decimal slot.

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

Notice that the value in the thousandths place value slot is a 4, which is 4 or smaller.

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

Since the value in the thousandths place value slot is 4 or smaller, you can round it down to zero. Therefore, the 4 will disappear and we are left with the following result:

Final Answer: 64.01408 rounded to the nearest hundredth is 64.01

Figure 17: 64.01408 rounded to the nearest hundredth is 64.01

---

Conclusion: How to Round to the Nearest Hundredth

In math, it is important to know how to estimate and round numbers to make them easier to work with. This skill is especially important when it comes to working with decimal numbers.

By working through this step-by-step tutorial on rounding numbers to the nearest hundredth, you learned a simple 3-step process that you can use to round any number to the nearest hundredth. The 3-steps outlined in this guide are as follows:

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

Once you understand how to correctly apply these three steps, you can use them to solve any problem that requires you to round to the nearest hundredth. Using this method, we solved six different rounding practice problems where we had to round a given number to the nearest hundredth. Here is a quick review of our results:

• 4.253 → 4.25

• 4.257 → 4.26

• 88.7309 → 88.73

• 29.48736 → 29.49

• 8.495 → 8.50

• 64.01408 → 64.01

Need more help? If so, we suggest going back and working through this step-by-step guide again (practice makes perfect after all). You can also gain some more rounding practice by downloading some free topic-specific worksheets available on our free math worksheet libraries.

Keep Learning:

How to Round to the Nearest Thousandth (Step-by-Step Guide)

Continue your rounding journey by learning how to round to the nearest thousandth.

---

How to Round to the Nearest Tenth—Step-by-Step Guide

How to Round to the Nearest Tenth

Step-by-Step Guide: Rounding to the Nearest Tenth in 3 Easy Steps

Free Step-by-Step Guide: How to round to the nearest tenth.

Learning and understanding how to round numbers is an important and useful math skill that makes working with large numbers faster and easier.

When it comes to rounding decimals, learning how to round the nearest tenth decimal place is a pretty straightforward process provided that you understand a few vocabulary terms, the meaning of place value, and some simple procedure.

This free Step-by-Step Guide on Rounding to the Nearest Tenth will teach you everything you need to know about how to round a decimal to the nearest tenth and it cover the following topics:

• What is rounding in math?

• What does rounding “to the nearest tenth” mean in terms of place value?

• How do you round to the nearest tenth in 3 easy steps?

• Rounding to the nearest tenth examples

Now, lets begin learning how to round to the nearest tenth by recapping some important math vocabulary terms and concepts.

(Looking for help with rounding to the nearest hundredth and rounding to the nearest thousandth?)

What is rounding in math?

In math, rounding is the process of approximating that involves changing a number to a close value that is simpler and easier to work with. Rounding is done by replacing the original number with a new number that serves as a close approximation of the original number.

For example, if a new pair of basketball sneakers costs $99.88, you could use rounding to conclude that you will need $100 to purchase the sneakers. In this example, you would be rounding to the nearest whole dollar and the purpose of rounding would be to replace the actual cost of “ninety-nine dollars and eight-eighty cents” with an approximated value of “one hundred dollars,” since it is simpler and easier to work with.

Figure 01: You could use rounding to say that a pair of sneakers that actually costs $99.88 has an approximate cost of $100, since one hundred is simpler and easier to work with.

As shown in Figure 01 above, $100 is simpler and easier to work with than $99.88. So, if you had to estimate the cost of 7 pairs of basketball shoes, you could easier estimate that the cost would be $700 (since 7 x 100 = 700).

What is the significance of 5 when it comes to rounding?

The next important thing to remember when it comes to rounding is the significance of the number 5. When you first learn how to perform simple rounding, you may use a visual aid called a rounding hill as shown in Figure 02 below. A rounding hill shows how, when it comes to rounding, if whatever digit you are rounding is less than 5 (4 or less), you will round down. If whatever digit you are rounding is 5 or greater, you will round up. So, 5 is the cutoff for rounding up in any rounding scenario.

• If digit to the right of the number being rounded is 4 or less → round down

• If digit to the right of the number being rounded is 5 or greater → round up

For example, if you wanted to round 17 to the nearest ten, the result would be 20 since 7 is 5 or greater and you would have to round up.

• 17 → 7 is 5 or greater, so round up → 20

Conversely, if you wanted to round 13 to the nearest ten, the result would be 10 since 3 is 4 or less and you would have to round down.

• 13 → 3 is 4 or less, so round down → 10

Figure 02: The Rounding Hill illustrates the significance of 5 and how you can determine when to round up and when to round down.

What does rounding to the nearest tenth mean in terms of place value?

Now that you know what rounding is and when to round up or round down, the final concept that we need to review is place value.

In math, place value refers to the numerical value that a digit has by virtue of its position in the number.

For example, consider the number 3.57.

We can think of the number 3.57 as the sum of 3 ones, 5 tenths, and 7 hundredths.

A useful tool for visualizing place value is called a place value chart, where each place value has its own slot so you can clearly identify a given digits place value. Figure 03 below shows the number 3.57 within a place value chart, where you can clearly see that 3 is in the ones place, 5 is in the tenths place, and 7 is in the hundredths place.

▶ FREE DOWNLOAD: Blank Decimal Place Value Chart (PDF File)

Figure 03: A place value chart is a useful tool for identify each digit’s place value, especially when you are dealing with decimals.

If you want to learn how to round to the nearest tenth, then you will need to be able to correctly identify the place value of the tenths and hundredths place value, otherwise you will struggle to correctly round a decimal to the nearest tenth (more on why this is the case later on in this guide).

Keep Learning: Where is the hundredths place value in math?

Here are a few more examples of correctly identifying the tenths and hundredths decimal places:

• 4.12 → 1 is in the tenths decimal place and 2 is in the hundredths decimal place

• 52.783 → 7 is in the tenths decimal place and 8 is in the hundredths decimal place

• 0.3333 → 3 is in the tenths decimal place and 3 is in the hundredths decimal place

• 488.60 → 6 is in the tenths decimal place and 0 is in the hundredths decimal place

Figure 04: Examples of identifying the tenths and hundredths decimal place for 4.12, 52.783, 0.3333, and 488.6

How to Round to the Nearest Tenth in 3 Easy Steps

Now you are ready to work through a few examples where you have to round to the nearest tenth using our easy 3-step method, which works as follows:

• Step One: Identify the value in tenths place value slot and the hundredths place value slot

• Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

• Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

Let’s continue on to using these three steps to several practice problems.

---

Example #1: Round to the Nearest Tenth: 8.63

This first example is pretty simple. You are tasked with rounding to the nearest tenth the number 8.63.

Let’s go ahead and apply our 3-step method to solving this problem:

Step One: Identify the value in tenths place value slot and the hundredths place value slot

In this case, 6 is in the tenths place value slot and 3 is in the hundredths place value slot as shown in Figure 05 below.

Figure 05: For the number 8.63, 6 is in the tenths place value slot and 3 is in the hundredths place value slot.

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

For this example, 3 is in the hundredths place value slot. Since 3 is less than 5, we will have to round down in the final step.

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

As determined in step two, we will be rounding the hundredths place value digit, which is 3 in this example, down to zero. This effectively means that, when rounding to the nearest tenth, you must remove the hundredths value digit entirely and make the following conclusion:

Final Answer: 8.63 rounded to the nearest tenth is 8.6

This final result is illustrated in Figure 06 below. Now, let’s move onto a second example where you will have to round up to get your final answer.

Figure 06: Step One: Split the cubic polynomial into two groups

---

Example #2: Round to the Nearest Tenth: 32.87

For this next example, you can use the same 3-step approach to determine what is 32.8 rounded to the nearest tenth as follows:

Step One: Identify the value in tenths place value slot and the hundredths place value slot

For the number 32.87, 8 is in the tenths place value slot and 7 is in the hundredths place value slot as shown in Figure 07.

Figure 07: Rounding to the nearest tenth: The first step is to identify the digits in the tenths and hundredths place value slots.

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

For the second example, 7 is in the hundredths place value slot. Since the number 7 is greater than 5, we will have to round up in the last step.

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

We have already determined that finding 32.87 rounded to the nearest tenth will require rounding up. In this case, the 8 in the tenths decimal place will round up to a 9 and the hundredths decimal place will disappear.

Final Answer: 32.87 rounded to the nearest tenth is 32.9

This final answer is shown in Figure 08 below.

Figure 08: 32.87 rounded to the nearest tenth is 32.9

---

Example #3: Round to the Nearest Tenth: 119.308

Notice that this example includes a digit in the thousandths decimal place. While this is a larger number than the previous two examples, you can still use the 3-step process to find the value of 119.308 rounded to the nearest tenth.

Step One: Identify the value in tenths place value slot and the hundredths place value slot

In this example, for the number 119.308, 3 is in the tenths decimal place value slot, 0 is in the hundredths place value slot, and 8 is in the thousandths place value slot (although the 8 will not have any effect on how you solve this problem, and you can actually ignore it entirely and still correctly round 119.308 to the nearest tenth).

Figure 09: To find the value of 119.308 rounded to the nearest tenth, you only need to worry about the values in the tenths and hundredths place value slots (anything after that does not matter).

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

Continuing on, lets focus on the fact that 0 is in the hundredths place value slot for this third example.

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

Since 0 is less than 5, we will have to round it down to—zero. And since zero is already zero, all that you have to do is make it disappear entirely and conclude that:

Final Answer: 119.308 rounded to the nearest tenth is 119.3

This final answer is shown in Figure 10 below.

Figure 10: How to round to the nearest tenth: 119.308 can be rounded to 119.3

---

Example #4: Round to the Nearest Tenth: 90.352

Just like the last example, 90.352 includes a digit in the thousandths decimal place. And, just like the last example, you can ignore that digit entirely and apply the same 3-step method as follows:

Step One: Identify the value in tenths place value slot and the hundredths place value slot

The place value slots for 90.352 are as follows: 3 is in the tenths place value slot and 5 is in the hundredths place value slot. Again, you can ignore the 2 in the thousandths place value slot.

Figure 11: How to round to the nearest tenth: start by identifying the values of the tenths and hundredths place value digits

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

For the second step, our focus is on the 5 in the hundredths place value slot.

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

Since 5 is equal to 5 or greater, we will have to round up. Remember that 5 is the cutoff for rounding up, so this is an example where the number just meets the requirements for rounding up instead of down.

Final Answer: 90.352 rounded to the nearest tenth is 90.4

The entire process for solving example #4 is illustrated in Figure 12 below.

Figure 12: 90.352 rounded to the nearest tenth is equal to 90.4

---

Example #5: Round to the Nearest Tenth: 149.96

Are you starting to get the hang of using the three-step process to round numbers to the nearest tenth? Let’s try rounding 149.96 to the nearest tenth and find out:

Step One: Identify the value in tenths place value slot and the hundredths place value slot

For this fifth example, the digit in the tenths place value slot is 9 and the digit in the hundredths place value slot is 6, as shown in Figure 13 below.

Figure 13: The digit in the tenths place value slot is 9 and the digit in the hundredths place value slot is 6.

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

Moving on, note that the digit in the hundredths place value slot is 6, which is 5 or larger.

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

Since 6 is equal to 5 or greater, we will have to round up. However, notice that the digit in the tenths place value slot is a 9, which can not be rounded up to the next digit. In this case, the 9 will become a zero and the digit that gets rounded up is the one in the ones place value slot (the number directly to the left of the decimal point).

So, when you round 149.96 to the nearest tenth, the 9 becomes a zero and the number 149 gets rounded up to the next whole number as follows:

Final Answer: 149.96 rounded to the nearest tenth equals 150.0

Figure 14: 149.96 rounded to the nearest tenth is 150.0

---

Example #6: Round to the Nearest Tenth: 3.0499

Now let’s work through one final example of rounding a number to the nearest tenth.

Remember that you only need to know the digits in the tenths and hundredths place value slots to round correctly, and you can ignore any additional numbers.

Step One: Identify the value in tenths place value slot and the hundredths place value slot

For this final example, the digit in the tenths place value slot is 0 and the digit in the hundredths place value slot is 4, as illustrated in Figure 15 below.

Figure 15: Remember that, when it comes to rounding to the nearest tenth, you can ignore any additional numbers that come after the digit in the thousandths decimal slot.

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

Just as we did in all of the previous examples, the second step requires you to identify the value of the hundredths place value digit. For the number 3.0499, this value is 4.

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

4, the digit in the hundredths place value slot, is less than 5, so we will be rounding down. So, the disappears and the 0 in the tenths place value slot stays a 0 since it can not be rounded down any further.

Therefore, we can conclude that:

Final Answer: 3.0499 rounded to the nearest tenth equals 3.0

Figure 16: 3.0499 rounded to the nearest tenth is 3.0

---

How to Round to the Nearest Tenth: Conclusion

Rounding is an important math skill that every student must learn at some point. While rounding integers is relatively simple, the process, while similar, gets trickier when decimals are involved.

This step-by-step guide focused on teaching you how to round numbers to the nearest tenth (i.e. to the nearest tenth decimal place). By using the following 3-step method, you can successfully round any number involving decimals to the nearest tenth:

Step One: Identify the value in tenths place value slot and the hundredths place value slot

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

This method will work for rounding any number to the nearest tenth. To recap, we used this method to solve the following examples where we were given a decimal number and tasked with rounding it to the nearest tenth:

• 8.63 → 8.6

• 32.87 → 32.9

• 119.309 → 119.3

• 90.352 → 90.4

• 149.96 → 150.0

• 3.0499 → 3.0

If you need more practice, we recommend working through the six practice problems in this guide again and/or working through the free rounding practice worksheets available on our free math worksheet libraries.

Keep Learning:

How to Round to the Nearest Hundredth (Step-by-Step Guide)

Continue your rounding journey by learning how to round to the nearest hundredth.

---

How to Factorize a Cubic Polynomial

How to Factorize a Cubic Polynomial

Step-by-Step Guide: How to Factor a Cubic Polynomial in 3 Easy Steps

Free Step-by-Step Guide: How to factor a polynomial with a specific number of terms

In algebra, a cubic polynomial is an expression made up of four terms that is of the form:

• ax³ + bx² + cx + d

Where a, b, c, and d are constants, and x is a variable. Polynomials in this form are called cubic because the highest power of x in the function is 3 (or x cubed).

Unlike factoring trinomials, learning how to factorize a cubic polynomial can be particularly tricky because using any type of guess-and-check method is extremely difficult. However, you can easily learn how to factor a cubic polynomial by using the grouping method described in this guide.

This free Step-by-Step Guide on How to Factorize a Cubic Polynomial will cover the following key topics:

• What is a cubic polynomial?

• What does it mean to factorize a cubic polynomial?

• How to factor a cubic polynomial examples (step-by-step)

While learning how to factor cubic polynomials can be challenging at first, you can develop your skills pretty quickly just by working through practice problems step-by-step until you become more comfortable with factoring cubic polynomials. So, this guide was designed to teach you everything you need to know about how to factor a cubic polynomial. We recommend that you read through this guide from start to finish and work through each example by following along step-by-step. By the end, you will be able to quickly and accurately factorize a cubic polynomial.

Figure 01: How to Factorize a Cubic Polynomial

What is a cubic polynomial?

As previously mentioned, a cubic polynomial is a math expression that is of the form ax³ + bx² + cx + d, where a, b, c, and d are all constants and x is a variable, and typically has four terms. Note that x is not the only letter that can be used as a variable in a cubic polynomial. Also, the number in front of any variable is referred to as a coefficient.

Additionally, the terms of a cubic polynomial are the individual “pieces” of the expression, separated by an addition or subtraction sign.

For example, the cubic polynomial in Figure 01 above, x³ + 3x² + 2x + 6 has four terms:

• 1st Term: x³

• 2nd Term: 3x²

• 3rd Term: 2x

• 4th term: 6

Before you can learn how to factor a cubic polynomial, it is extremely important that you know how to recognize that given polynomial is cubic, so make sure that you deeply understand what a cubic polynomial is before moving forward in this guide.

Figure 02: Factoring a Cubic Polynomial

What does it mean to factorize a cubic polynomial?

In math, the factors of any polynomial represent components or “building blocks” of the polynomial. Whenever you factor a polynomial (cubic or otherwise), you are finding simpler polynomials whose product equals the original polynomial. Each of these simpler polynomials is considered a factor of the original polynomial.

For example, the binomial x² - 100 has two factors (x + 10) and (x-10).

Why? Lets take a look at what happens when we find the product of the factors by double distributing:

• (x+10)(x-10) = x² + 10x - 10x - 100 = x² + 0 - 100 = x² - 100

Notice that the result was the original polynomial, x² - 100.

Since cubic polynomials (four terms) are more complex than binomials (two terms), their factors will also be a little more complex, but the idea is still the same—factoring a cubic polynomial involves finding simpler polynomials or “building blocks” whose product is the original cubic polynomial.

And, to factorize a cubic polynomial, we will be using a strategy called grouping that will allow you to factor any cubic polynomial (assuming that it is factorable at all) using 3 easy steps. So, lets go ahead and work three practice problems to give you some experience with factoring cubic polynomials by grouping.

Now that you understand the key terms and the difference between a polynomial with 2 terms, 3 terms, and 4 terms.

For factoring each type of polynomial, we will look at two methods: GCF, direct factoring, and, sometimes, a combination of the two.

Let’s get started!

---

How to a Factorize a Cubic Polynomial Examples

Now, you will learn how to use the follow three steps to factor a cubic polynomial by grouping:

Step One: Split the cubic polynomial into two groups of binomials.

Step Two: Factor each binomial by pulling out a GCF

Step Three: Identify the factors

As long as you follow these three steps, you can easily factor a given polynomial, though note that not all cubic polynomials are factorable."

We will start by factoring the cubic polynomial shown in Figure 01: x³ + 3x² + 2x + 6

Example #1: Factor x³ + 3x² + 2x + 6

Figure 03: We have to find the factors of x³ + 3x² + 2x + 6

To factorize this cubic polynomial, we will be applying the previously mentioned 3-step method as follows:

Step One: Split the cubic polynomial into groups of two binomials.

To factor this cubic polynomial, we will be using the grouping method, where the first step is to split the cubic polynomial in half into two groups.

Figure 04: The first step to factoring a cubic polynomial is to split it into groups of two binomials.

For Example #1, at the end of the first step, you have split the cubic binomial down the middle to form two groups of binomials:

• (x³ + 3x²)

• (2x + 6)

Why are you splitting the cubic polynomial like this? Notice that it is not possible to pull a Greatest Common Factor (GCF) out of the original cubic polynomial x³ + 3x² + 2x + 6. The goal of the first step is to create two separate binomials, each with a GCF that can be “pulled out.”

Figure 05: Make sure that each individual binomial has a GCF before moving onto the next step.

Step Two: Factor each binomial by pulling out a GCF

Again, the purpose of the first step is to split the cubic polynomial into two binomials, each with a GCF. Before moving forward, ensure that each individual binomial has a GCF; otherwise, you may need to swap the positions of the middle terms (3x² and 2x). Swapping these middle terms is not required for this first example; however, we will work through an example later on where this is required.

Now, for step two, you can divide the GCF out of each grouping as follows:

• (x³ + 3x²)→ x²(x +3)

• (2x + 6) → 2(x + 3)

This process of pulling the GCF out of each binomial is illustrated in Figure 05 below.

Figure 06: To factorize a cubic function, split it into two groups and then pull a GCF out of each group.

Step Three: Identify the factors

After completing the second step, you are left with:

• x²(x +3) + 2(x+3)

Notice that both groups share a common term, which, in this case, is (x+3). This result is expected and is a signal that you are factoring the cubic polynomial correctly. If the groups do not share a common terms, then it is likely that the cubic polynomial is not factorable or that you made a mistake pulling out the GCF.

However, since you factored each group and ended up with a common factor of (x+3), you can move on to determining the factors of the cubic polynomial.

The illustration in Figure 06 above color-codes how you use the results from step two to determine the factors of the cubic polynomial.

You already know that one of the factors is (x+3). To find the other factor, you can simply take the two “outside” terms, in this case, x² and +2.

• x²(x +3) + 2(x+3) → (x²+2)(x+3)

Final Answer: The factors of x³ + 3x² + 2x + 6 are (x²+2) and (x+3)

The entire 3-step method that we just used to factor a cubic polynomial by grouping is shown in Figure 07 below:

Figure 07: How to factorize a cubic polynomials step-by-step

How can you check if your factors are actually correct? You can perform double distribution to multiply the binomials together to see if the result is indeed the cubic polynomial that you started with. If it is, then you know that you have factorized correctly.

You can see in Figure 08 below that multiplying the factors together does indeed result in the original cubic polynomial, so you know that your factors are correct:

• (x²+2)(x+3) = x³ + 3x² + 2x + 6

Figure 08: Check your answer using double distribution

Now, lets go ahead and work through another example of how to factor a cubic polynomial.

---

Example #2: Factor 2x³ - 3x² + 18x - 27

Just like in the first example problem, you can use the 3-steps for factoring a cubic polynomial by grouping as follows:

Figure 09: Find the factors of the cubic polynomial 2x³ - 3x² + 18x - 27

Step One: Split the cubic polynomial into groups of two binomials.

After splitting this cubic polynomial, you end up with these two groups: (2x³ - 3x²) and (18x-27)

Figure 10: Step One: Split the cubic polynomial into two groups

Step Two: Factor each binomial by pulling out a GCF

Next, divide a GCF out of each group (if possible) as follows:

• (2x³ - 3x²) → x²(2x - 3)

• (18x - 27) → 9(2x - 3)

This process of pulling a GCF out of each group is illustrated in Figure 11 below:

Figure 11: Factorize a cubic polynomial

Step Three: Identify the factors

Since both factors have a common term, (2x-3), you know that you have likely factored correctly and you can move onto identifying the factors.

Final Answer: (x²+9) and (2x-3) are the factors of the cubic polynomial 2x³ - 3x² + 18x - 27.

All of the steps for solving Example #2 are illustrated in Figure 12 below.

Figure 12: The factors are (x²+9) and (2x-3)

Just like the last example, you can check to see if your final answer is correct by multiplying the factors together and seeing if the result equals the original cubic polynomial.

Example #3: Factor 3y³ + 18y² + y + 6

Finally, lets work through one more example where you have to factorize a cubic polynomial.

Step One: Split the cubic polynomial into groups of two binomials.

Again, the first step is to split the cubic polynomial down the middle into two binomials as shown in Figure 13 below.

Figure 13: Factoring a cubic polynomial by grouping.

As shown in Figure 13 above, splitting the polynomial down the middle leaves you with these two groups: (3y³ +18y²) and (y+6)

Remember that the whole point of splitting the cubic polynomial is to create two binomials that each have a GCF. But notice that the second binomial, (y+6), is not factorable because there is no GCF between +y and +6.

But, as previously mentioned, this doesn’t mean that you can not solve this problem further. In fact, the commutative property of addition allows you to swap the positions of the two middle terms (18y² and +y).

This extra step of swapping the two middle terms is illustrated in Figure 14 below.

Figure 14: Sometimes you have to swap the positions of the middle terms in order to factorize a cubic polynomial.

After swapping the positions of the middle terms, you can now apply the 3-step method to factoring the equivalent polynomial: 3y³ + y + 18y² + 6 (this new cubic polynomial is equivalent to the original because the commutative property of addition allows you to rearrange the terms without changing the value of the expression).

Now, you actually can split the new cubic polynomial into groups that can be factoring by dividing out a GCF: (3y³ + y) and (18y² + 6)

Figure 15: After swapping the positions of the middle terms, you can continue on with factoring the cubic polynomial.

Step Two: Factor each binomial by pulling out a GCF

As shown in Figure 15 above, you can factor each group by pulling out a GCF as follows:

• (3y³ + y) → y(3y² + 1)

• (18y² + 6) → 6(3y² + 1)

Step Three: Identify the factors

Finally, you can conclude that:

Final Answer: The factors are (y+6) and (3y² + 1)

The step-by-step process to solving this 3rd example are shown in Figure 16 below. Again, you can make sure that your final answer is correct by multiplying the factors together and verifying that their product is equivalent to the original cubic polynomial.

Figure 16: How to factorize a cubic polynomial when you have to swap the middle terms.

---

How to Factorize a Cubic Polynomial: Conclusion

It is beneficial to understand how to factorize a cubic polynomial because the skill will allow you to simplify and understand the behavior of cubic functions as you continue onto higher levels of algebra and begin to explore topics like finding roots, analyzing graphs, and solving cubic equations.

Factoring cubic functions can be challenging, but you can always use the following 3-step grouping method described in this guide to successfully factor a cubic polynomial (assuming that it is factorable in the first place):

Step One: Split the cubic polynomial into groups of two binomials.

Step Two: Factor each binomial by pulling out a GCF

Step Three: Identify the factors

Keep Learning:

How to Factor Polynomials (step-by-step guide for students)

---