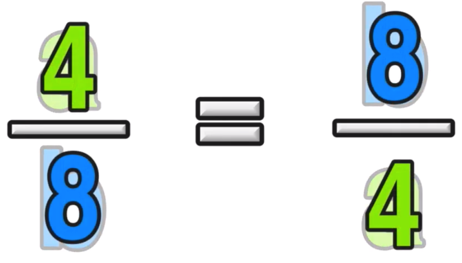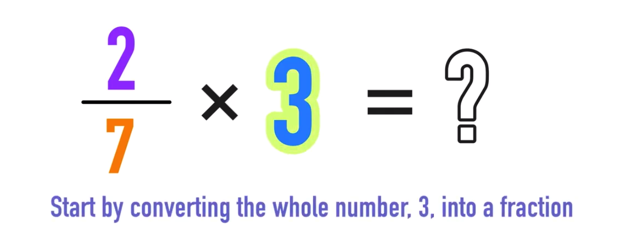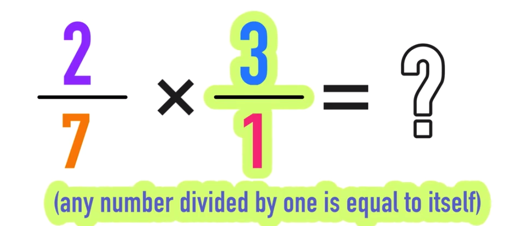Here is Everything You Need to Know About the Commutative Property
What is the commutative property in math and what does it look like?
Welcome to this free lesson guide that accompanies this Commutative Property Explained! video lesson, where you will learn the answers to the following key questions and information:
What is the commutative property of addition?
What is the commutative property of multiplication?
Commutative Property Examples
Commutative Property Proof
This Complete Guide to the Commutative Property includes several examples, a step-by-step tutorial, an animated video mini-lesson, and a free worksheet and answer key.
*This lesson guide accompanies our animated Commutative Property Tutorial on YouTube.
Want more free math lesson guides and videos? Subscribe to our channel for free!
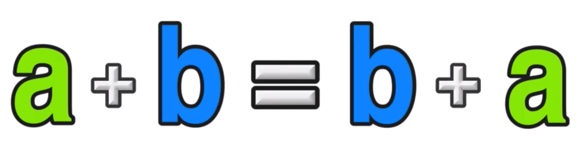
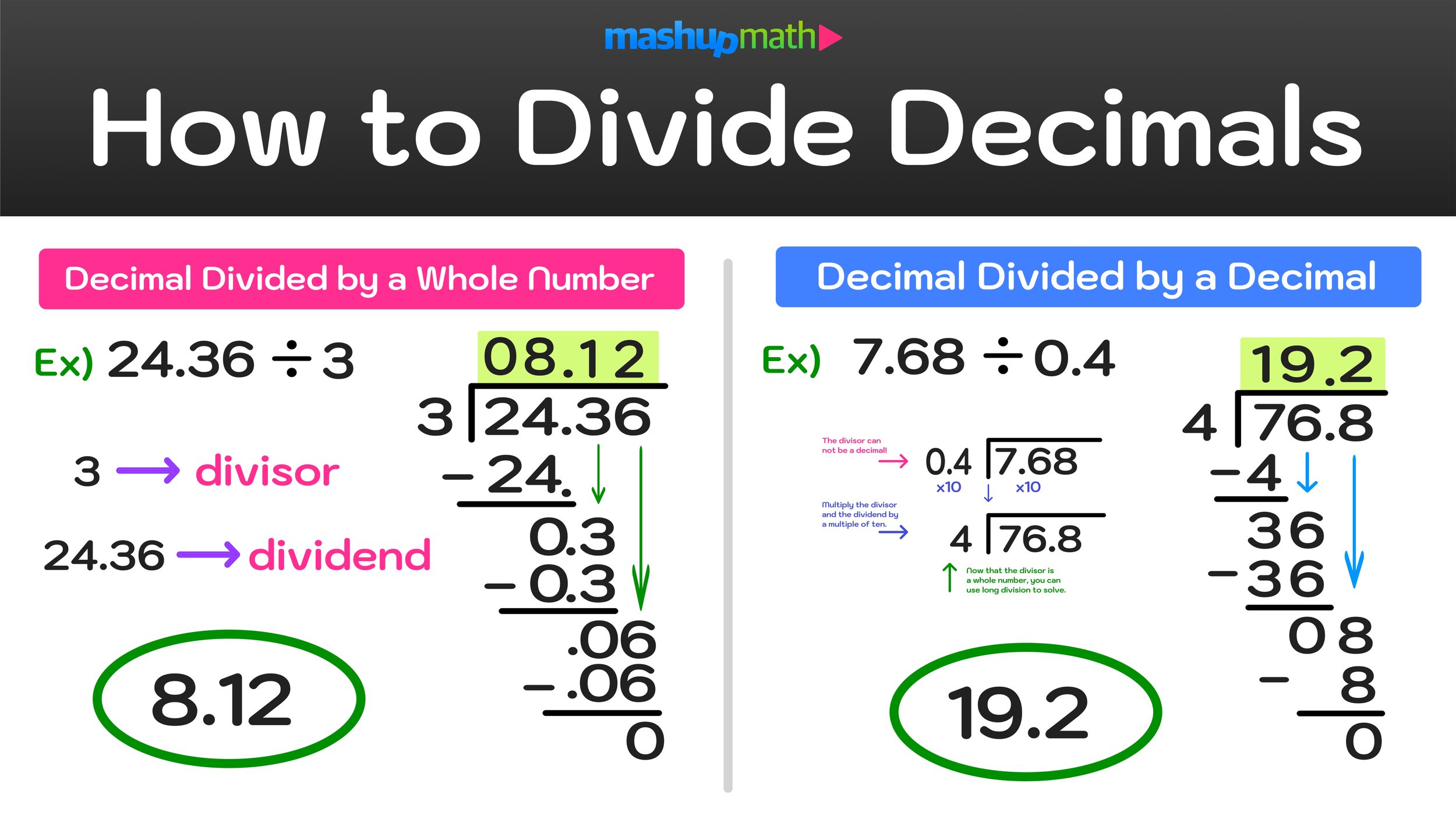
What is the Commutative Property of Addition?
The Commutative Property of Addition states that for any real numbers a and b:
Notice that the terms are in reverse order!
If you replace the a and b terms with real numbers, like a = 2 and b =8 as shown below:
You can see from this example that, even though the terms are in reverse order on each side of the equal sign, that each side is equal to 10.
This is an example of why the commutative property holds under addition!
Does the Commutative Property work with subtraction?
Now that you understand the commutative property of addition, what about subtraction?
Is this true???
For example, if you replace the a and b terms with real numbers, like a = 2 and b =8 as shown below:
You can see from this example that, even though the terms are in reverse order on each side of the equal sign, that each side is NOT equal ( -6 does not equal 6)
This is an example of why the commutative property does NOT hold under addition!
Summary: Addition is commutative, but Subtraction is not!
What is the Commutative Property of Addition?
The Commutative Property of Multiplication states that for any real numbers a and b:
Notice that the terms are in reverse order!
For example, if you replace the a and b terms with real numbers, like a = 4 and b =8 as shown below:
You can see from this example that, even though the terms are in reverse order on each side of the equal sign, that each side is equal to 32.
This is an example of why the commutative property holds under multiplication!
Does the Commutative Property work with division?
Now that you understand the commutative property of multiplication, what about division?
Is this true???
For example, if you replace the a and b terms with real numbers, like a = 4 and b =8 as shown below:
You can see from this example that, even though the terms are in reverse order on each side of the equal sign, that each side is NOT equal ( one-half does not equal 2)
This is an example of why the commutative property does NOT hold under division!
Summary: Multiplication is commutative, but Division is not!
Final Word: Commutative Property Definitions
In summary, the commutative property only works with addition and multiplication. It does not work with subtraction and division.
For all real numbers a and b:
Commutative Property of Addition Definition: a + b = b + a
Commutative Property of Multiplication Definition: (a)(b) = (b)(a)
The terms are the same, but the order is reversed!
Commutative Property Explained: Video Tutorial
Still confused? Check out the animated video lesson below:
Check out the video lesson below to learn more about the commutative property and to see more commutative property examples:
Extra Practice: Free Commutative Property Worksheet
Free Worksheet!
Are you looking for some extra practice? Click the links below to download your free worksheets and answer key:
Identifying The Commutative Property:
CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET
Keep Learning with More Free Lesson Guides:
Have thoughts? Share your thoughts in the comments section below!
(Never miss a Mashup Math blog--click here to get our weekly newsletter!)
By Anthony Persico
Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.