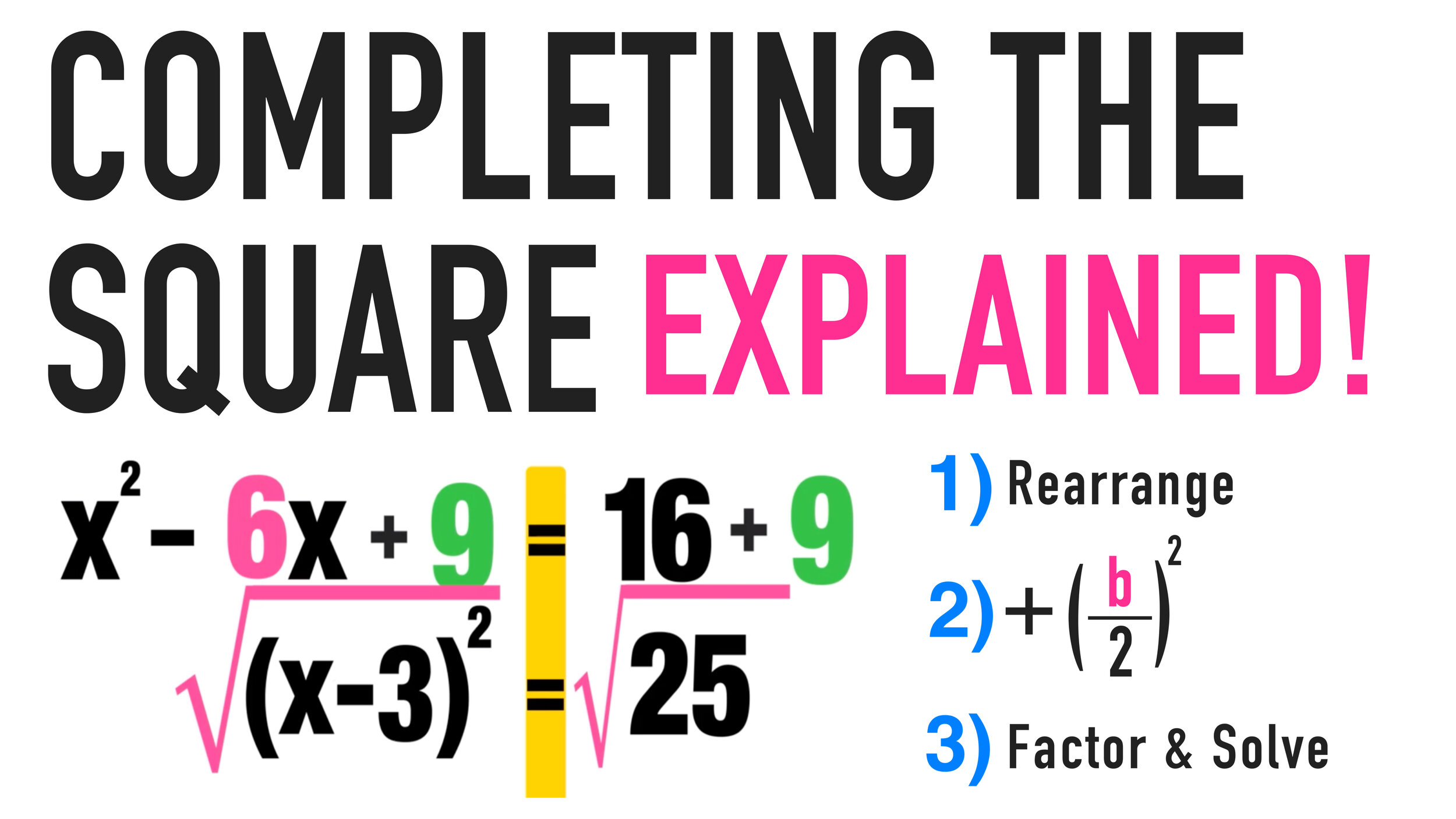Jelly Bean Day Math Puzzles for Grades 1-6! (April 22)

Can Your Kids Solve These Jelly Bean Day Math Puzzles?

Did you know that April 22nd is National Jelly Bean Day? 

You can celebrate by getting yourself a big bag of Jelly Bellys and making them disappear. My favorite flavors are Pina Colada and Cinnamon, while I absolutely despise the popcorn and black licorice flavors (am I the only one who feels this way about jelly bean flavors?)

And you can make your Jelly Bean Day math lesson extra special and memorable for your kids by doing any or all of the following:

First, you can start by sharing a few of these 11 Super Cute and Funny Math Jokes and Puns for Kids.

And you can keep the fun going with 3 Jelly Bean Day Math Puzzles!

These kinds of activities are best used for warm-ups (anticipatory sets), cooldowns and exit tickets, and transitions. They are especially good for helping your students develop problem-solving skills, mathematical reasoning, and applying the order of operations.

I like to share fun math puzzles like today’s at least once per week to keep my lessons fresh and exciting, and my students love them!

Today’s Jelly Bean Day Math Challenges for grades 1-6 are sample puzzles from the best-selling workbook: The Big Book of Super Fun Math Puzzles for Grades 1-6.

The activities are tiered by difficulty using the following system:

Pink Level (Grades 1-2) | Blue Level (Grades 3-4) | Green Level (Grades 5-6+)

Jelly Bean Day Math Puzzles for Grade 1 through 6+

Note that:

(answer keys to follow)

Pink Level Puzzle ( for Grades 1-2)

Extra Resources: Which One Doesn't Belong? Free Math Activities for Grades 1-8

Blue Level Puzzle (for Grades 3-4)

Free Math Resources: Free Math Coloring Worksheets for 3rd and 4th Grade

Green Level Puzzle (for Grades 5-6+)

Bonus! Would you like over 300 more math puzzles like todays?

Click here to take a closer look at our best-selling The Big Book of Math Puzzles for Students in Grades 1-6 and access more free sample puzzles with answer keys!

And click here to get your copy of The Big Book of Super Fun Math Puzzles for Grades 1-6 as a PDF download.

And here are the answers to the Jelly Bean Day Math Puzzles:

---

Sharing fun math puzzles with your students is just one effective strategy for improving student engagement. Subscribe to our mailing list here to get more free daily resources, lesson plans, ideas, and insights for K-12 math teachers in your inbox every week.

Read More Posts About Math Education:

---

By Anthony Persico

Anthony is the lead educator and founder of Mashup Math. He lives in Denver, Colorado and is also a YouTube for Education partner. Follow him on Twitter at @mashupmath.

The Standard Equation of a Circle Formula: Everything You Need to Know!

How to Write and Graph the Standard Equation of a Circle

The following Standard Equation of a Circle Formula examples will show you everything you need to know!

Welcome to this free lesson guide that accompanies this Standard Equation of a Circle Explained! Tutorial where you will learn the answers to the following key questions and information:

• What is the standard equation of a circle definition?

• How can I find the equation of a circle given center and radius?

• How can I find the equation of a circle given center and diameter?

• How can I find the equation of a circle given a graph of the circle?

This Complete Guide to the Standard Equation of a Circle includes several examples, a step-by-step tutorial, an animated video mini-lesson, and a free equation of a circle worksheet and answer key.

---

*This lesson guide accompanies our animated Standard Equation of a Circle Explained! video on YouTube.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

Standard Equation of a Circle Definition

Before you learn the standard equation of a circle formula, let’s quickly review the basic properties of circles:

The radius of a circle is any line that extends from the center of the circle to the edge.

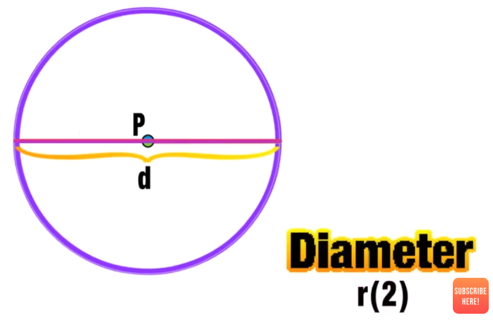
The diameter of a circle is any straight line that extends from one edge of the circle through the center and to the opposite side. The value of the diameter is two times the radius.

• Radius = half the length of the diameter

• Diameter = twice the length of the radius

The Standard Equation of a Circle Formula:

The standard equation formula of a circle formula above is not as intimidating as it looks.

Let’s break it down:

You only need to know two pieces of information to write the standard equation of a circle:

• The Center Point Coordinates (h,k) where h is the x-value and k is the y-value

• The length of the radius r

That’s it! Now let’s look at an example:

How to Find the Standard Equation of a Circle Formula

Example 1

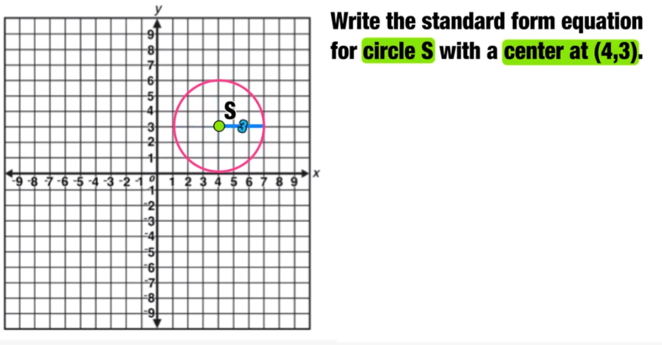
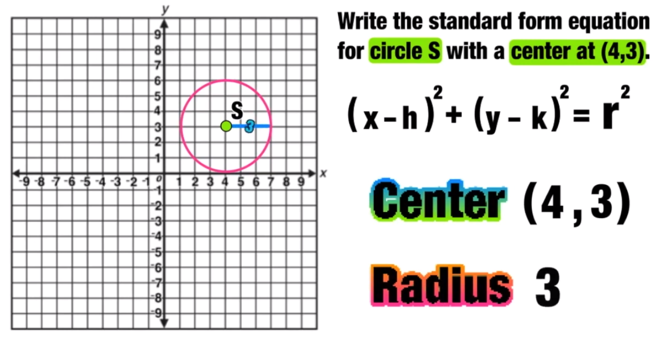
Write the standard form equation for circle S with a center at (4,3).

Remember that you only need two pieces of information to write the standard equation of a circle: the coordinates of the center point, and the length of the radius.

In this example, the center point is at (4,3) and the radius is 3 (you can find the length of the radius by drawing a horizontal line from the center of the circle to the edge and counting the number of spaces).

h=4, k=3, and r=3

Now you can replace h with 4 and k with 3 to complete the left side of the equals sign and then r^2 with 3^2 (which equals 9) to complete the ride side as follows:

This is the standard equation of Circle S

Example 2

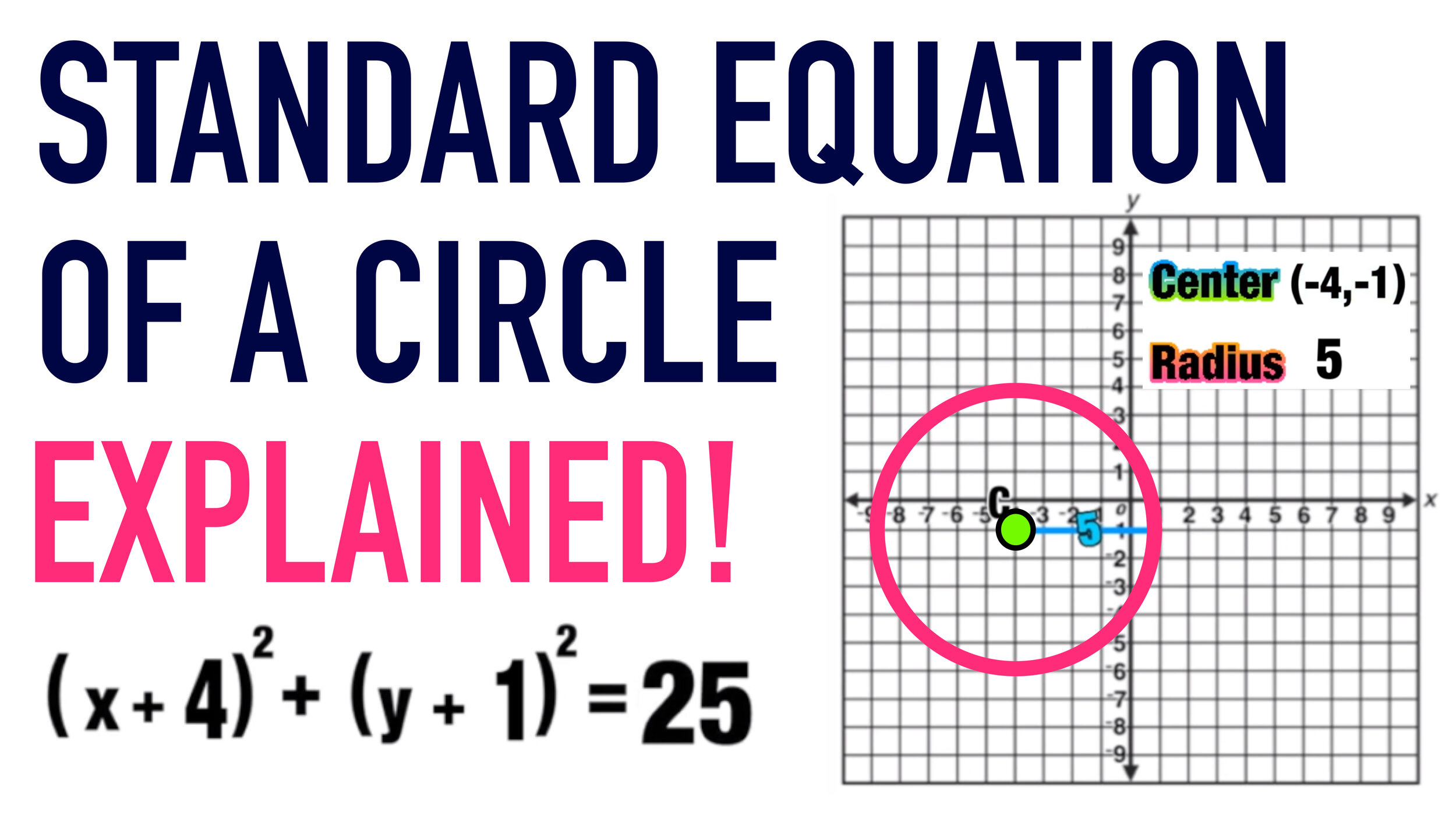
Write the standard form equation for circle C with a center at (-4,-1).

Remember that you only need two pieces of information to write the standard equation of a circle: the coordinates of the center point, and the length of the radius.

In this example, the center point is at (-4,-1) and the radius is 5 (you can find the length of the radius by drawing a horizontal line from the center of the circle to the edge and counting the number of spaces).

Now you can replace h with -4 and k with -1 as follows (remember that two negatives make a positive!) and r with 5 as follows:

Remember that double negatives become positive!

This is the standard equation of Circle C.

EXAMPLE 3

Write the standard form equation for Circle J with a center at the origin and a diameter of 18.

To write the equation of Circle J, you need to know the center coordinates and the length of the radius.

You already know that the center is at the origin, which is (0,0) so h=0 and k=0

And you also know that the diameter is 18, and since a radius equals one half of the diameter, r = 18/2 = 9, so the radius is 9.

Now you can write the equation of the circle as follows:

The graph of Circle J.

This is the standard equation of Circle J.

---

---

Example 4

*On this last example, you will work in reverse and identify the center coordinates and radius given the standard equation of a circle.

Start by finding the coordinates of the center of Circle P as follows:

Circle P has a center at (7,0)

Now you just have the find the value of the radius r. The value 196 represents r^2, so, to find the value of r, you have to figure out what number squares equals 196 as follows:

The radius of Circle P is 14 because 14^2 equals 196.

Answer: Circle P has a center at (7,0) and a radius of 14.

The trinomial factors to (x+1)(x+1) or (x+1)^2

---

---

Standard Equation of a Circle Formula: Video Tutorial

Still confused? Check out the animated video lesson below:

Check out the video lesson below to learn more about the standard equation of a circle formula and to see more completing the square problems solved step-by-step:

Equation of a Circle Word Problems (Advanced Practice)

Looking for more advanced practice with the standard equation of a circle? The following video lesson covers topics including:

• equation of a circle word problems

• finding equation of a circle given two points

• using distance and midpoint formulas to find the equation of a circle

---

Extra Practice: Free Equation of a Circle Worksheet

Free Worksheet!

Are you looking for some extra practice? Click the links below to download your free worksheets and answer key:

Equation of a Circle Worksheet:

CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Completing the Square Formula: Your Step-by-Step Guide

How to Solve Quadratic Equations by Completing the Square Formula

What is the Completing the Square Formula and how can you use it to solve problems?

Welcome to this free lesson guide that accompanies this Completing the Square Explained! video tutorial, where you will learn the answers to the following key questions and information:

• What is the completing the square formula?

• How can I solve by completing the square?

• How can I master solving quadratic equations by completing the square?

• What are the completing the square steps?

This Complete Guide to the Completing the Square includes several examples, a step-by-step tutorial, an animated video mini-lesson, and a free worksheet and answer key.

---

*This lesson guide accompanies our animated Completing the Square Explained! YouTube.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

When can you use the completing the square method to solve quadratic equations?

Solving by completing the square is used to solve quadratic equations in the following form:

Note that a quadratic can be rearranged by subtracting the constant, c, from both sides as follows:

Figure 1

These are two different ways of expressing a quadratic.

Keep this in mind while solving the following problems:

Completing the Square Formula

The following method is less of a formula and more like completing the square steps:

Example: Solve the following quadratic by completing the square.

Note that a=1 and b=-6

Notice that a=1, and b=-6, but what about the constant, c?

Completing the Square Step 1 of 3: Rearrange if Possible

To complete the square, you need to have all of the constants (numbers that are not attached to variables) on the right side of the equals sign.

In this example, you can achieve this by subtracting 9 from both sides and simplifying as follows:

View fullsize

Now that you have rearranged the quadratic so that all of the constants are on the right side of the equals sign, you are ready for step 2!

Completing the Square Step 2 of 3: +(b/2)^2 to both sides

The second step to solving by completing the square is to add (b/2)^2 to both sides of the equation.

Remember the alternate way to write a quadratic from Figure 1 earlier on? Let’s look at it again with our current equation directly below it for reference.

Figure 1

Step two requires that you add (b/2)^2 to both sides and it should be clear that, in this example, b equals -6.

So to find the value of (b/2)^2, just plug in -6 for b and solve as follows:

In this case, (b/2)^2 equals 9

Since (b/2)^2 equals 9, go ahead and add 9 to both sides of the equals sign as follows:

You can simplify the right side of the equal sign by adding 16 and 9.

Notice that you can simplify the right side of the equal sign by adding 16 and 9 to get 25.

Now you are ready for the final step!

Completing the Square Step 3 of 3: Factor and Solve

Notice that, on the left side of the equation, you have a trinomial that is easy to factor.

The factors of the trinomial on the left side of the equals sign are (x-3)(x-3) or (x-3)^2

Completing the square will allows leave you with two of the same factors.

Expressing the factors are (x-3)^2 instead of (x-3)(x-3) is very important because it allows you to solve the problem as follows:

Simplify by taking the square root of both sides.

This is what is left after taking the square root of both sides.

After taking the square root of both sides, you are left with x-3 = +/- 5.

Next, to get x by itself, add 3 to both sides as follows.

And to find your solutions, simply perform x = 3 + 5 AND x = 3 - 5 to get your answer as follows:

Answer: x= 8 and x = -2

This method will apply to solving any quadratic equation! Let’s quickly review the completing the square formula method steps below and then take a look at a few more examples.

Solving by Completing the Square Steps Method Review:

---

---

Solve by Completing the Square Problems

Example 1:

Solve for x by completing the square.

STEP 1/3: REARRANGE IF NECESSARY

Start by moving all of the constants to the right side of the equals sign as follows:

Leave yourself some room to work with!

STEP 2/3: +(b/2)^2 to both sides

In this example, b=2, so (b/2)^2 = (2/2)^2 = (1)^2 = 1

So, the next step is to add 1 to both sides as follows:

STEP 3/3: Factor and Solve

For the final step, factor the trinomial on the left side of the equals sign and solve for x as follows:

The trinomial factors to (x+1)(x+1) or (x+1)^2

The square root of 8 is approximately 2.83

These are the solutions!

Answer: x=1.83 and x=-3.83

---

---

Solve by Completing the Square Examples

Example 2:

Solve for x by completing the square.

On this final example, follow the complete the square formula 3-step method for finding the solutions* as follows:

*Note that this problem will have imaginary solutions.

Step 1/3: Move the constants to the right side.

Step 2/3: Add (b/2)^2 to both sides.

Step 3/3: Factor and Solve

You can get a more detailed step-by-step explanation of how to solve the above example by watching the video tutorial below starting from minute 7:36.

Completing the Square Explained: Video Tutorial

Still confused? Check out the animated video lesson below:

Check out the video lesson below to learn more about the completing the square and to see more completing the square problems solved step-by-step:

---

Extra Practice: Free Completing the Square Worksheet

Free Worksheet!

Are you looking for some extra practice? Click the links below to download your free worksheets and answer key:

Completing the Square Practice Worksheet:

CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

How to Use Volume of a Sphere Formula: Your Complete Guide

Here is Everything You Need to Know About Finding the Volume of a Sphere

How can you use the volume of a sphere formula to solve problems?

Welcome to this free lesson guide that accompanies this Volume of a Sphere video tutorial, where you will learn the answers to the following key questions and information:

• How do you find volume of a sphere?

• How do you use the volume of a sphere formula?

• What is the radius of a sphere?

• What is the circumference of a sphere?

This Complete Guide to Finding Volume of a Sphere includes several examples, a step-by-step tutorial, an animated video mini-lesson, and a free worksheet and answer key.

---

*This lesson guide accompanies our animated Volume of a Sphere Tutorial on YouTube.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

Volume of a Sphere: Properties

Before you learn about finding the volume of a sphere and how to use the volume of a sphere formula, you must be familiar with the following properties of a sphere:

• A sphere is a three-dimensional circle (like a ball)

• The radius of a sphere is any line that extends from the center to the edge.

• The radius, r, is equal to half of the diameter.

Volume of a Sphere Formula and Definition

Next, you need to understand what the volume of a sphere is.

The Volume of a Sphere is how much room is INSIDE of a sphere.

The Volume of a Sphere Formula:

Not that, unlike area or surface area, volume is measured in cubic units.

Now you are ready to solve some problems involving volume of a sphere!

Using The Volume of a Sphere Formula Examples

EXAMPLE: How many cubic centimeters of air would be needed to completely fill a soccer ball with a diameter of 22cm?

Let’s start by identifying the key information as follows:

Since you are concerned with filling the amount of space inside of the soccer ball, you know that this problem can be solved using the volume of a sphere formula.

And you also know that the ball has a diameter of 22cm…

Since you know the length of the diameter and that the radius is equal to half of the diameter, you can conclude that the radius of the soccer ball equals 11cm, because (22/2)=11…

Now you are ready to use the formula to solve the problem as follows:

Start by replacing r with 11 in the volume of a sphere formula.

Then evaluate using your calculator.

Finally, you can conclude that:

ANSWER: The volume of the sphere is approximately 5,575.3 cubic centimeters!

---

---

Using The Volume of a Sphere Formula Explained: Video Tutorial

Still confused? Check out the animated video lesson below:

Check out the video lesson below to learn more about how to use the volume of a sphere formula:

---

Free Volume of a Sphere Worksheet

Free Worksheet!

Are you looking for some extra practice? Click the links below to download your free worksheets and answer key:

Volume of a Sphere Practice Worksheet:

CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

The Commutative Property: Everything You Need to Know

Here is Everything You Need to Know About the Commutative Property

What is the commutative property in math and what does it look like?

Welcome to this free lesson guide that accompanies this Commutative Property Explained! video lesson, where you will learn the answers to the following key questions and information:

• What is the commutative property of addition?

• What is the commutative property of multiplication?

• Commutative Property Examples

• Commutative Property Proof

This Complete Guide to the Commutative Property includes several examples, a step-by-step tutorial, an animated video mini-lesson, and a free worksheet and answer key.

---

*This lesson guide accompanies our animated Commutative Property Tutorial on YouTube.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

What is the Commutative Property of Addition?

The Commutative Property of Addition states that for any real numbers a and b:

Notice that the terms are in reverse order!

If you replace the a and b terms with real numbers, like a = 2 and b =8 as shown below:

You can see from this example that, even though the terms are in reverse order on each side of the equal sign, that each side is equal to 10.

This is an example of why the commutative property holds under addition!

Does the Commutative Property work with subtraction?

Now that you understand the commutative property of addition, what about subtraction?

Is this true???

For example, if you replace the a and b terms with real numbers, like a = 2 and b =8 as shown below:

View fullsize

You can see from this example that, even though the terms are in reverse order on each side of the equal sign, that each side is NOT equal ( -6 does not equal 6)

This is an example of why the commutative property does NOT hold under addition!

Summary: Addition is commutative, but Subtraction is not!

---

---

What is the Commutative Property of Addition?

The Commutative Property of Multiplication states that for any real numbers a and b:

Notice that the terms are in reverse order!

For example, if you replace the a and b terms with real numbers, like a = 4 and b =8 as shown below:

You can see from this example that, even though the terms are in reverse order on each side of the equal sign, that each side is equal to 32.

This is an example of why the commutative property holds under multiplication!

Does the Commutative Property work with division?

Now that you understand the commutative property of multiplication, what about division?

Is this true???

For example, if you replace the a and b terms with real numbers, like a = 4 and b =8 as shown below:

You can see from this example that, even though the terms are in reverse order on each side of the equal sign, that each side is NOT equal ( one-half does not equal 2)

This is an example of why the commutative property does NOT hold under division!

Summary: Multiplication is commutative, but Division is not!

---

---

Final Word: Commutative Property Definitions

In summary, the commutative property only works with addition and multiplication. It does not work with subtraction and division.

For all real numbers a and b:

Commutative Property of Addition Definition: a + b = b + a

Commutative Property of Multiplication Definition: (a)(b) = (b)(a)

The terms are the same, but the order is reversed!

---

---

Commutative Property Explained: Video Tutorial

Still confused? Check out the animated video lesson below:

Check out the video lesson below to learn more about the commutative property and to see more commutative property examples:

---

Extra Practice: Free Commutative Property Worksheet

Free Worksheet!

Are you looking for some extra practice? Click the links below to download your free worksheets and answer key:

Identifying The Commutative Property:

CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.