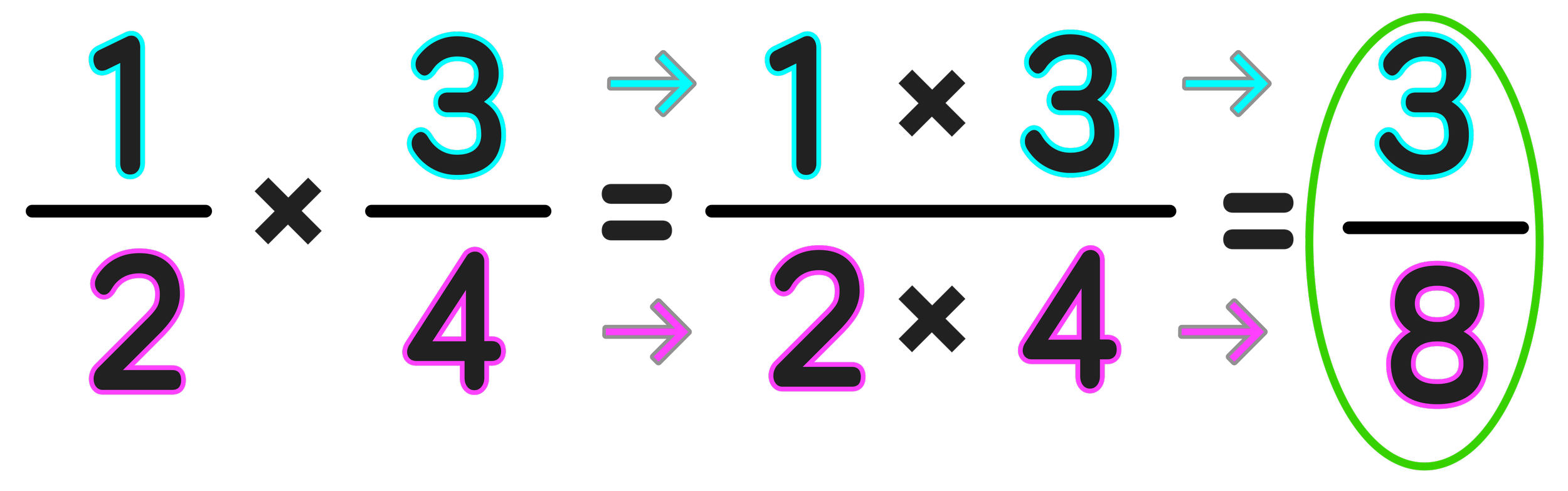How to Multiply Fractions in 3 Easy Steps
Math Skills: Learn how to multiply fractions by fractions, how to multiply fractions with whole numbers, and how to multiply mixed fractions.
Free Step-by-Step Guide: How to Multiply Fractions Explained
Once you have learned how to add fractions and how to subtract fractions, you are ready to start multiplying fractions in a variety of scenarios.
This free guide will teach you everything you need to know about how to multiply fractions in the following ways:
The task of having to multiply fractions together may seem challenging at first, but the procedure is actually quite simple and something that you can learn by working through a handful of practice problems, which is exactly what we will be doing in this free step-by-step guide.
While we highly recommend that you work through the guide from start to finish, you can use the quick-links above to jump to a particular topic section.
For all of the problems in this guide, we will be using an easy 3-step strategy that can be used to solve any problem where you have to multiply fractions to get a solution. So, if you can learn how to follow three easy steps, you can correctly answer any multiplying fractions problem!
Are you ready to get started?
Before we start working on the multiplying fractions practice problems, let’s do a quick recap of some key vocabulary terms related to fractions.
How to Multiply Fractions: Vocabulary Recap
This guide uses several math vocabulary terms related to fractions that you will need to be familiar with in order to learn this new math skill. Be sure that you understand the meaning of the following key vocabulary terms before moving forward in this guide.
The Numerator of a Fraction
For any fraction, the numerator is the number at the top of the fraction. For example, the fraction 4/5 has a numerator of 4 since 4 is at the top of the fraction.
The Denominator of a Fraction
For any fraction, the denominator is the number at the bottom of the fraction. For example, the fraction 4/5 has a denominator of 5 since 5 is at the bottom of the fraction.
In this guide, any mention of a numerator is referring to the top number of a fraction and any mention of a denominator is referring to bottom number of a fraction. This relationship between the numerator and the denominator of a fraction is illustrated in Figure 01-A below.
Figure 01-A: In any fraction, the numerator is the top number and the denominator is the bottom number.
Moving on, let’s recap three more key vocabulary terms and concepts related to fractions:
Whole Numbers
A whole number refers to any number that does not contain any fractions or decimals (i.e. an integer). Some examples of whole numbers include 4, 51, and 263.
Note that any whole number can be expressed in fraction form by rewriting it as a fraction with a denominator of 1. For example, the number 4 can be rewritten as a fraction as 4/1. This fact will come in handy later on when you learn how to multiply a fraction by a whole number.
Figure 01-B: How to Rewrite a Whole Number as a Fraction: Rewrite the given whole number as a fraction with a denominator of 1.
Proper Fractions
A fraction is a number that represents a part of a whole number. 1/4, 3/5, and 7/8 are all examples of fractions.
Note that proper fractions have a numerator that is smaller than the denominator.
Mixed Fractions (Mixed Numbers)
A mixed fraction (or a mixed number) is any number that represents the sum of a whole number and a proper fraction. For example, 7 5/8 is a mixed number that is equal to the sum of 7 and 5/8.
Note that mixed fractions can also be expressed as improper fractions (fractions whose numerator is greater than its denominator).
Figure 02: What is the difference between a whole number, a fraction, and a mixed number.
Now that you are familiar with these vocabulary terms, you’re ready to learn how to multiply fractions using our easy 3-step strategy.
How to Multiply Fractions by Fractions
How to Multiply Fractions by Fractions: Example #1
Example #1: 1/2 x 3/4
To solve this first example, where we are tasked with finding the product of 1/2 (one-half) and 3/4 (three-quarters), we will use the following three-step strategy for multiplying fractions:
How to Multiply Fractions in 3 Easy Steps
Step One: Multiply the numerators together.
Step Two: Multiply the denominators together.
Step Three: See if the resulting fraction can be simplified or reduced.
When it comes to multiplying fractions, the process is extremely straightforward, and you can use these three steps to solve any fraction multiplication problem!
So, let’s go ahead and use these three steps to solve this first problem: 1/2 x 3/4 = ?
Step One: Multiply the numerators together.
For this problem, we have two fractions: 1/2 x 3/4
The first step requires us to multiply the two numerators (top numbers) together as follows:
1 x 3 = 3
Step Two: Multiply the denominators together.
The second step requires us to multiply the two denominators (bottom numbers) together as follows:
2 x 4 = 8
Step Three: See if the resulting fraction can be simplified or reduced.
Now we have a new fraction with a numerator of 3 and a denominator of 8:
1/2 x 3/4 = 3/8
For the final step, we have to see if the result can be further simplified or reduced. If it can’t, our result will be our final answer.
In this case, 3/8 can not be simplified or reduced any further and we can conclude that:
Final Answer: 1/2 x 3/4 = 3/8
Figure 03 below illustrates how we solved the first example using the three-step strategy.
Figure 03: How to Multiply Fractions: Multiply the numerators together, then multiply the denominators together. Finally, simplify the resulting fraction if possible and you’re done!
Note that it’s okay if you are still a little confused. The more experience you gain using this 3-step strategy to multiply fractions, the easier these type of problems will become. Let’s go ahead and work through another example.
How to Multiply Fractions by Fractions: Example #2
Example #2: 5/6 x 4/7
Let’s go ahead and solve Example #2 exactly the same as we did the previous example.
Step One: Multiply the numerators together.
For step one, we have to find the product of the two numerators, 5 and 4:
5 x 4 = 20
Step Two: Multiply the denominators together.
For step two, we have to find the product of the two denominators, 6 and 7:
6 x 7 = 42
Step Three: See if the resulting fraction can be simplified or reduced.
Our result is a fraction with a numerator of 20 and a denominator of 42:
5/6 x 4/7 = 20/42
Can the result, 20/42, be reduced? The answer is yes, because both numbers have a greatest common factor of 2. So, after dividing both the numerator and the denominator by 2, we can conclude that:
Final Answer: 5/6 x 4/7 = 20/42 = 10/21
Figure 04 below illustrates how we determined that 5/6 x 4/7 = 10/21
Figure 04: How to Multiply Fractions: Be sure to express your answer in reduced form.
Next, let’s go ahead and solve one more practice problem where we’ll have to multiply one fraction by another fraction.
How to Multiply Fractions by Fractions: Example #3
Example #3: 9/16 x 7/12
Again, we can use the same three-step strategy to solve this third example as follows:
Step One: Multiply the numerators together.
In this case, the numerator of the first fraction is 9 and the numerator of the second fraction is 7.
9 x 7 = 63
Step Two: Multiply the denominators together.
In this case, the denominator of the first fraction is 16 and the denominator of the second fraction is 12.
16 x 12 = 192
Step Three: See if the resulting fraction can be simplified or reduced.
Now we have a new fraction with a numerator of 62 and a denominator of 192:
9/16 x 7/12 = 63/192
To see if this result can be reduced, we have to see if 63 and 192 both share a GCF. Since both of these numbers are divisible by 3, we can divide both the numerator and the denominator by 3 to get our final answer in reduced form:
Final Answer: 9/16 x 7/12 = 63/192 = 21/64
The graphic in Figure 05 below shows we successfully multiplied two fractions in this example.
Figure 05: How to Multiply Fractions Step-by-Step.
Now that you have some experience with multiplying fractions, let’s move onto the next section where you will learn how to multiply a fraction by a whole number and how to multiple a whole number by a fraction.
How to Multiply Fractions with Whole Numbers
The second section of this guide will focus on how to multiply a fraction with by a whole number and how to multiply a whole number by a fraction.
Luckily, the three-step method that we used to solve problems in the previous section will work here as well. If you are unfamiliar with how to multiply a fraction by a fraction, we highly recommend that you go back and work through the above examples.
Now, let’s jump into our first example on how to multiply fractions with whole numbers!
How to Multiply a Fraction by a Whole Number: Example #1
Example #1: 3/8 x 2
When learning how to multiply fractions with whole numbers, it is important to remember that any whole number can be rewritten as an equivalent fraction by rewriting it as a fraction with a denominator of 1.
Since any whole number can be expressed as a fraction in this way, we can solve problems where you have to multiply a fraction by a whole number simply by rewriting the whole number as a fraction and then using the same 3-step strategy from the previous section to solve it.
For this example, we can rewrite the whole number, 2, as 2/1 and rewrite the original problem as:
3/8 x 2 → 3/8 x 2/1
Now, we can find the product by using our three steps:
Step One: Multiply the numerators together.
In this case, the numerator of the first fraction is 3 and the numerator of the second fraction is 2.
3 x 2 = 6
Step Two: Multiply the denominators together.
In this case, the denominator of the first fraction is 8 and the denominator of the second fraction is 1.
8 x 1 = 8
Step Three: See if the resulting fraction can be simplified or reduced.
Finally, we are left with a new fraction with a numerator of 6 and a denominator of 8:
3/8 x 2/1 = 6/8
And, since 6 and 8 are both divisible by 2, we know that the fraction 6/8 can be simplified to:
Final Answer: 3/8 x 2/1 = 6/8 = 3/4
Figure 06 illustrates how we solved this problem.
Figure 06: How to Multiply a Fraction by a Whole Number: Rewrite the whole number as a fraction with a denominator of 1.
Next, let’s take a look at another example of how to multiply fractions by whole numbers.
How to Multiply a Fraction by a Whole Number: Example #2
Example #2: 5/8 x 6
For this next practice problem, we can rewrite the whole number, 6, as 6/1 and rewrite the original problem as:
5/8 x 6 → 5/8 x 6/1
From here, we can solve this problem as follows:
Step One: Multiply the numerators together.
Start by multiplying the numerators of both fractions together:
5 x 6 = 30
Step Two: Multiply the denominators together.
Next, continue with multiplying the denominators of both fractions together:
8 x 1 = 8
Step Three: See if the resulting fraction can be simplified or reduced.
Here we have a resulting fraction with a numerator of 30 and a denominator of 8:
5/8 x 6/1 = 30/8
Notice that this result is an improper fraction since the numerator, 30, is greater than the denominator, 8. We can reduce this result down to 15/4 and leave it as our final answer or we can convert 15/4 to a mixed number, 3 3/4.
Final Answer: 5/8 x 6/1 = 30/8 = 15/4 or 3 3/4
The graphic in Figure 07 shows how we solved solve this problem by multiplying fractions by whole numbers.
Figure 07: How to Multiply a Fraction by a Whole Number Step-by-Step.
How to Multiply a Whole Number by a Fraction: Example #3
Example #3: 9 x 2/3
Notice that this third example requires you to multiply a whole number by a fraction (rather than a fraction by whole number like in the last two examples). Since multiplication is associative, the order of the terms won’t change the way that you solve the problem, so we can again use our three-step strategy as follows:
First, just like the previous two examples, rewrite the whole number (9 in this case) as a fraction with a denominator of 1.
9 x 2/3 → 9/1 x 2/3
Step One: Multiply the numerators together.
Multiply the numerators together as follows:
9 x 2 = 18
Step Two: Multiply the denominators together.
Multiply the denominators together as follows:
1 x 3 = 3
Step Three: See if the resulting fraction can be simplified or reduced.
The resulting fraction has a numerator of 18 and a denominator of 3:
9/1 x 2/3 = 18/3
The resulting improper fraction, 18/3, can be simplified. Since both 18 and 3 share a GCF of 3, we can perform 18/3 = 6/1 = 6 and conclude that
Final Answer: 9/1 x 2/3 = 18/3 = 6
All of the steps for solving this example are shown in Figure 08 below.
Figure 08 How to Multiply a Whole Number by a Fraction Step-by-Step
How to Multiply a Whole Number by a Fraction: Example #4
Example #4: 12 x 7/8
For this next example, we have to rewrite the whole number (12 in this case) as a fraction with a denominator of 1 and then use our three-step strategy to solve:
12 x 7/8 → 12/1 x 7/8
Step One: Multiply the numerators together.
For step one, multiply both of the numerators:
12 x 7 = 84
Step Two: Multiply the denominators together.
For step two, multiply both of the denominators:
1 x 8 = 8
Step Three: See if the resulting fraction can be simplified or reduced.
The result is a new fraction with a numerator of 84 and a denominator of 8:
12/1 x 7/8 = 84/8
Now we have to see if 84/8 can be simplified. Both 84 and 8 share a GCF of 4, so after dividing both numbers by 4, the result is 21/2. While 21/2 can not be simplified further, it is an improper fraction that can be expressed as a mixed number, 10 1/2.
Final Answer: 12/1 x 7/8 = 84/8 = 21/2 or 10 1/2
Figure 09 below illustrates how we were able to multiply a whole number by a fraction to solve this problem.
Figure 12: Whenever you end up with an improper fraction, you will likely have to convert it to a mixed number.
Now that you know how to multiply a fraction by a whole number and how to multiply a whole number by a fraction, it’s time to move onto the final section where we will go over how to multiply mixed fractions.
How to Multiply Mixed Fractions
How to Multiply Fractions with Mixed Numbers: Example #1
Example #1: 3/5 x 4 1/2
Multiplying fractions with mixed numbers can be done using our same three-step strategy, but with one small extra step at the very beginning.
Before you can solve this problem, you will have to convert the mixed number into an improper fraction.
For this example, the mixed number 4 1/2 can be rewritten as 9/2 (both of these are equivalent):
3/5 x 4 1/2 → 3/5 x 9/2
Now, we can solve 3/5 x 9/2 to find the answer to this problem as follows:
Step One: Multiply the numerators together.
Start off multiplying the numerators of both fractions:
3 x 9 = 27
Step Two: Multiply the denominators together.
Continue by multiplying the denominators of both fractions:
5 x 2 = 10
Step Three: See if the resulting fraction can be simplified or reduced.
After steps one and two, we are left with the improper fraction 27/10.
3/5 x 9/2 = 27/10
While 27/10 can not be simplified, it can be expressed as the mixed number 2 7/10.
Final Answer: 3/5 x 9/2 = 27/10 = 2 7/10
Note that 27/10 is technically a correct answer, but most problems requiring you to multiply mixed fractions will call for you to express your final answer as a mixed fraction.
See Figure 10 for step-by-step details of how we solved this problem.
Figure 10: How to Multiply Fractions with Mixed Numbers
Moving on, let’s work through one final practice problem where we will have to multiply a mixed number by another mixed number.
How to Multiply Mixed Fractions: Example #2
Example #2: 4 1/5 x 3 2/3
For this example, notice that there are two mixed numbers.
Similar to the previous example, you will have to convert both mixed numbers into equivalent improper fractions before you can use the three-step strategy to solve:
4 1/5 = 21/5
3 2/3 = 11/3
Now we can go ahead and find the answer by solving 21/5 x 11/3
Step One: Multiply the numerators together.
First, find the product of the numerators of both fractions:
21 x 11 = 231
Step Two: Multiply the denominators together.
Next, find the product of the denominators of both fractions:
5 x 3 = 15
Step Three: See if the resulting fraction can be simplified or reduced.
Finally, we are left with the improper fraction 231/15
21/5 x 11/3 = 231/15
While 231/15 is a pretty ugly improper fraction, it can actually be simplified since 231 and 15 share a GCF of 3. So, after dividing both numbers by 3, we are left with 77/5.
21/5 x 11/3 = 231/15 = 77/5
Assuming that we have to express our final answer as a mixed number, we lastly have to rewrite 77/5 as 15 2/5 and we have solved the problem!
Final Answer: 21/5 x 11/3 = 231/15 = 77/5 = 15 2/5
The graphic in Figure 11 below illustrates how we used the 3-step method to solve this problem.
Figure 14: How to Multiply Fractions with Mixed Numbers (Step-by-Step)
Conclusion: How to Multiply Fractions
Multiplying fractions is an important math skill that you can master with a little bit of practice.
This guide shared a simple and effective 3-step strategy that you can use to solve any problem requiring you to multiply fractions together in any of the following scenarios:
multiplying fractions by other fractions
multiplying fractions by whole numbers
multiplying whole numbers by fractions
multiplying mixed fractions
multiplying mixed numbers
The good news is that the 3-step strategy shared in this guide can be used to solve problems for all of the above scenarios and can be summarized as follows:
Step One: Multiply the numerators together.
Step Two: Multiply the denominators together.
Step Three: See if the resulting fraction can be simplified or reduced.
The more practice you get using these three steps, the better at multiplying fractions you will become!
Keep Learning
Search Tags: how to subtract fractions, subtracting fractions, how to subtract fractions with different denominators, fraction subtraction, subtracting fractions with unlike denominators, how do you subtract fractions?