How to Find the Area of a Circle in 3 Easy Steps

How to Find the Area of a Circle in 3 Easy Steps

How to Find the Area of a Circle

Step-by-Step Guide: How to Find Area of a Circle with Radius, How to Find Area of a Circle with Diameter

 

Free Step-by-Step Guide: How to find the area of a circle explained.

 

In math, it is important to be able to calculate the area of a shape (i.e. the total space that a shape takes up) by using a formula.

When it comes to finding the area of a circle, you can easily find the area as long as you know the area of a circle formula and the length of the circle’s radius or diameter.

This free Step-by-Step Guide on How to Find the Area of a Circle will teach you how to use the circle formula, A=πr², to find area of a circle and it will cover the following topics:

You have the option of either following this guide on how to find area of a circle in step-by-step order, or you can use the hyperlinks above to skip to any particular section of interest.

Now, before we get into any examples of how to find the area of a circle, let’s do a review of important vocabulary terms and characteristics of circles that we can later on apply to solving our sample problems.

Are you ready to get started?

 

Figure 01: What are the key properties of circles?

 

What is the Area of a Circle?

In order to understand what the area of a circle actually represents, it’s important that you are familiar with some key properties of circles:

  • Every circle has a center point.

  • The circumference of a circle (also known as the edge or perimeter of the circle) is the outer boundary of the circle. All points on the edge of a circle are equidistant from the center point.

  • The diameter of a circle is a line that passes through the center point and touches two points on the edge of the circle. Any diameter will cut the circle in half.

  • The radius of a circle is a line segment that starts at the center and ends on the edge of the circle. Any radius will always be equal to half the length of the circle’s diameter.

All of these key properties are highlighted for Circle P in Figure 01 above.

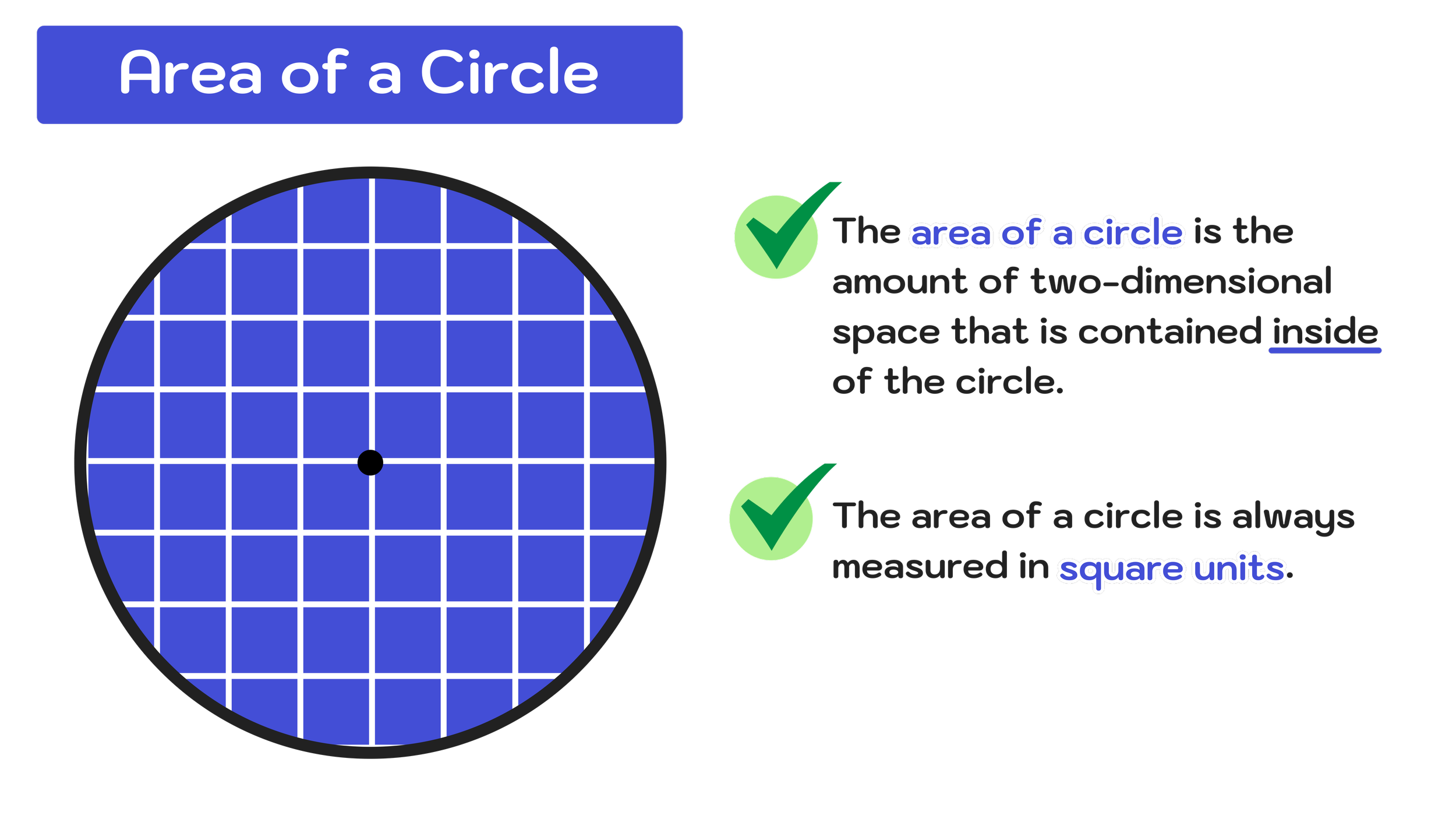
The area of a circle is the amount of two-dimensional space that is contained inside of the circle. Area is measured in square units.

What does this mean in real-world terms? If you wanted to figure out the size of the region contained within a particular circle, you would simply have to calculate its area. For example, if you wanted to tile the bottom of a circular swimming pool, knowing the size of the pool’s area would help you to determine how many square units of tile you would need to cover the entire region.

This real-world example is illustrated in Figure 02 below.

 

Figure 02: Real-world application of finding the area of a circle. (Image: Mashup Math MJ)

 

While many math problems involving circles with simply include two-dimensional diagrams of circles, the idea is still the same. The key takeaway here is that the area of a circle is the size of the region encompassed within the circle. The larger the circle, the larger its area will be. And, since circles are two-dimensional figures (i.e. they are flat), the area will be measured in square units.

Figure 03 illustrates this concept and what it means when we say that the area of a circle will always be expressed in square units.

Notice that many of the squares are “cut off” and incomplete, so we should expect to have answers that include decimals rather than whole numbers (we will see this more when we get to the practice problems later on).

For now, just make sure that you are comfortable with the key properties of circles (especially the difference between the radius of a circle and the diameter of a circle) and what the area of a circle represents before moving onto the next section where we will learn the area of a circle formula.

 

Figure 03: What is the area of a circle?

 

Area of a Circle Formula: A=πr²

You can find the area of a circle by using the area of a circle formula: A=πr² (where r is the length of the radius of the circle).

Whenever you are calculating a circle’s area using the area of a circle formula, you can use pi (π) or an approximation of pi (π≈3.14).

Before moving forward, make sure that you remember the area of a circle formula and that the r in the formula represents the length of the radius of whatever circle whose area you are trying to find. The diagram in Figure 04 below can serve as a reference for remembering the area of a circle formula. You may also wish to write the formula down before moving onto the practice problems later on in this guide.

 

Figure 04: The area of a circle formula.

 

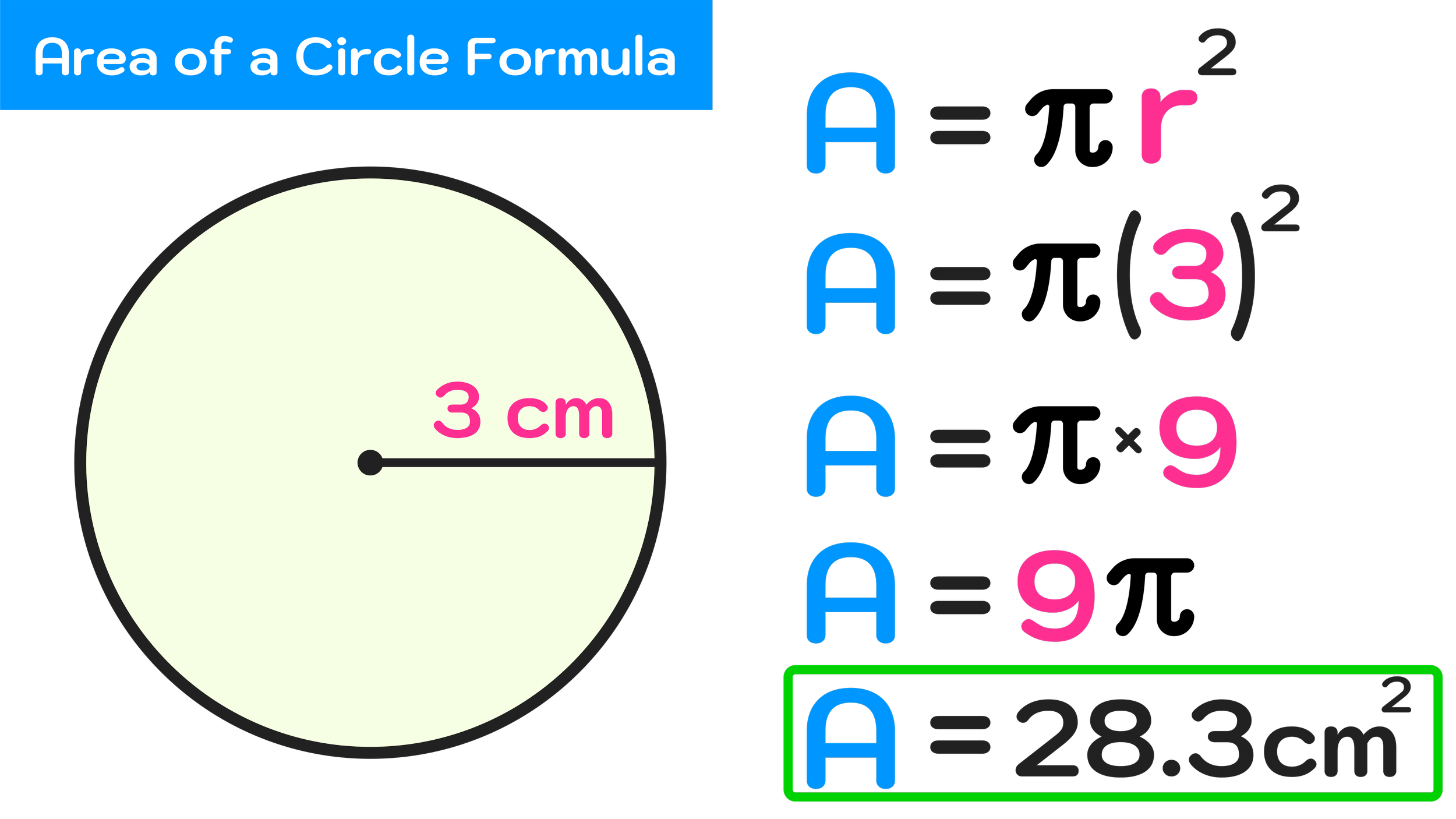
For example, if we wanted to find the area of a circle with a radius of 3 cm, we could use the area of a circle formula to determine the approximate amount of square inches that make up the region inside of the circle.

In this case,

  • A=πr²

  • r=3

So, to find the area of this circle, we would simply have to substitute r with 3 and then evaluate to find the area as follows:

  • A=πr²

  • A=π(3)²

  • A=π9 or A=9π

  • A=28.27433388…

  • A=28.3 cm²

As shown above, we know that area equals π times 3². Since we know that 3²=9, we can now say that area equals π times 9 (or 9π). Finally, we can put 9π into a calculator to get 28.27433388….

In this guide, we will find area to the nearest tenth of a square unit, so we can approximate our final answer as A=28.3 cm².

These steps are illustrated in Figure 05 below.

 

Figure 05: How to use the area of a circle formula to find the area of a circle.

 

Next, let’s move onto working on a few more examples of how to find the area of a circle with a given radius or a given diameter. Then, we will take a look at how to find the area of a half circle.

How to Find Area of a Circle with a Radius

In the example shown in Figure 05 above, we found the area of a circle with a radius of 3cm using the area of a circle formula A=πr².

Whenever you have to find the area of a circle where the radius is given, you can simply input the given value of r (the radius of the circle) into the area of a circle formula and evaluate to find the value of the area.

And we will go ahead and do exactly that in the example below.

Example #1: Find the Area of a Circle with Radius 7 mm

For this example, we have to find the area of a circle with a radius of 7 mm.

We can easily find the area of using the area of a circle formula, A=πr², by substituting r with 7 as follows:

  • A=πr²

  • A=π(7)²

  • A=π49 or A=49π

  • A=153.93804…

  • A=153.9 mm²

That’s all that there is to it! Whenever you know the length of the radius of a circle, r, you can input that value into the area of a circle formula to figure out its area.

The steps for solving this first example are illustrated in Figure 06 below. Make sure that you are comfortable with finding the area of a circle with a given radius using the area of a circle formula before moving onto the next section where we will learn how to find area of a circle with diameter.

 

Figure 06: How to Find the Area of a Circle Step-by-Step

 

How to Find Area of a Circle with Diameter

While students often have a relatively easy time with finding the area of a circle when they know the value of its radius (as shown in the previous section), they can sometimes get confused when they have to find the area of a circle with diameter given instead of radius.

However, you can still use the area of a circle formula, A=πr², to find the area of a circle with a diameter, but with one small extra step.

Remember that the radius of a circle is a line segment that starts at the center and ends on the edge of the circle and that any radius will always be equal to half the length of the circle’s diameter.

In other words, the diameter of a circle is equal to twice the length of the circle’s radius. Or, vice versa, the radius of a circle is equal to half the length of a circle’s diameter.

So, if you know the diameter of a circle, then you can simply divide it by two to find its radius.

For example, consider a circle with a diameter of 10 feet. This means that the circle has a radius of 5 feet. And, if you know the radius of a circle, then you can use the area of a circle formula to calculate its area.

Let’s go ahead and learn how to find the area of a circle with diameter with this in mind by working through the examples below.

 

Figure 07: The radius of any circle is equal to one half the length of its diameter.

 

Example #2: Find the Area of a Circle with Diameter 24 yd

For this example, we have to find the area of a circle with a diameter of 24 yards.

Just like the previous examples, we can use the area of a circle formula, A=πr², to find the area of the circle in question.

However, we can’t use the formula just yet because we only know the length of the diameter and not the radius. So, in order to find the value of the radius, r, we have to first have to divide the diameter by two to find the value of r as follows:

  • r=d/2

  • r=24/2

  • r=12

So, if the circle has a diameter of 24 yards, then it also has a radius of 12 yards (because 24÷2=12).

Now that we know the value of r (r=12 in this case), we can substitute it into the area of a circle formula and solve as follows:

  • A=πr²

  • A=π(12)²

  • A=π144 or A=144π

  • A=452.3893421…

  • A=452.4 yd²

And that is how to find area of a circle with diameter!

Just remember that you can always determine the length of a circle’s radius by dividing its diameter by two. And once you know a circle’s radius, you can use the formula A=πr² to find its area.

 

Figure 08: How to find the area of a circle with diameter by using the area of a circle formula.

 

Next, let’s look at another example of how to find area of a circle with diameter in a real world context.

Example #3: Find the Area of a Circle with Diameter 57 m.

For this next example, we want to find the area of a circular zen garden with a diameter of 57 meters.

Again, we can solve this problem by using the area of a circle formula A=πr².

Since we know that the circle has a diameter of d=57, we can use that given information to find the length of the radius as follows:

Figure 09: Find the area of a circular zen garden with 57 m diameter.

  • r=d/2

  • r=57/2

  • r=28.5

Remember that we can always find the length of a circle’s radius simply by dividing its diameter by two. In this case, 57/2=28.5 so we can say that r=28.5 (note that it’s totally fine to have a radius that is a decimal value).

So, if the circular zen garden has a diameter of 57 m, then it also has a radius of 28.5 m (because 57÷2=28.5).

Now that we know that r=28.5, we can substitute it into the area of a circle formula and solve as follows:

  • A=πr²

  • A=π(28.5)²

  • A=π812.25 or A=812.25π

  • A=2,551.758633…

  • A=2,551.8 m²

We can now conclude that the circular zen garden has an approximate area of 2,551.8 square meters and we have solved the problem!

 

Figure 10: Real world example of how to find the area of a circle with diameter given.

 

Now, let’s move onto the final section where we will learn how to find the area of a half circle.

How to Find Area of a Half Circle

Now that you know how to find the area of a circle with a given radius or diameter using the area of a formula circle, you are ready to learn how to find the area of a half circle (also known as a semicircle).

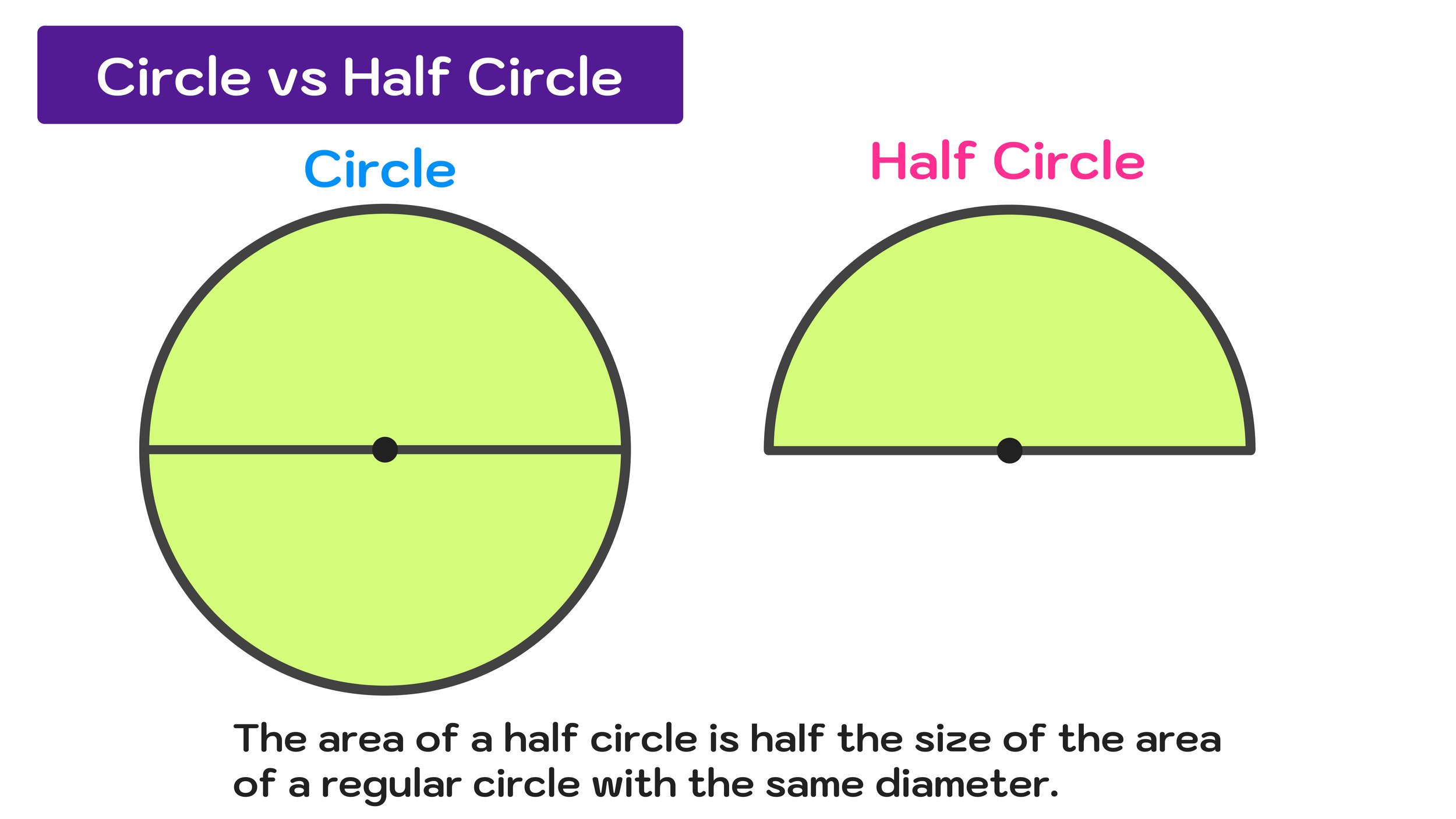
What is a half circle? Simply put, a half circle is a regular circle that has been cut in half along the diameter.

And, notably, the area of a half circle is exactly one half the area of a regular circle with the same diameter.

The differences between a circle and a half circle are illustrated in Figure 11 below.

 

Figure 11: What is the difference between the area of a circle and the area of a half circle?

 

With this difference in mind, we will have to use a modified version of the area of a circle formula to find the area of a half circle.

  • Area of a Circle Formula: A=πr²

  • Area of a Half Circle Formula: A=(πr²)/2

Notice that the area of a half circle formula is the same as the area of a circle formula except that the result is being dividing by 2. This should make sense because the area of a half circle is half the size of the area of a regular circle with the same diameter.

 

Figure 12: The area of a half circle formula is A=(πr²)/2

 

Now that you know the area of a half circle formula, let’s learn how to find the area of a half circle step-by-step.

Example #4: Find the Area of a Half Circle with Diameter 22 cm

For this example, we have to find the area of a half circle with a diameter of 22 cm.

To solve this problem, we can use the area of a half circle formula: A=(πr²)/2

Let’s start by figuring out the value of r (the radius of the half circle), which can determine by cutting the diameter in half as follows:

  • r=d/2

  • r=22/2

  • r=11

Now that we know the value of r (r=11 in this example), we can substitute it into the area of a half circle formula and solve as follows:

  • A=(πr²)/2

  • A=(π(11)²)/2

  • A=(121π)/2

  • A=190.0663555…

  • A=190.1 cm²

And that is how to find area of a half circle using the area of a half circle formula.

All of the steps for solving this example are illustrated in Figure 13 below.

 

Figure 13: How to Find Area of a Half Circle

 

Example #5: Find the Area of a Half Circle

For this final example, let’s learn how to find the area of a circle (namely a half circle) in a real-world scenario.

In this case, we have a circular shaped table with a surface that is half-covered with tile and half-covered with hardwood and we want to find the area of the portion that is covered in hardwood.

If we know that the table has a diameter of 13 feet, we can find the length of the radius use the area of a half circle formula to solve the problem as follows:

  • r=d/2

  • r=13/2

  • r=6.5

Now that we know that r=6.5, we can substitute it into the area of a half circle formula and solve as follows:

  • A=(πr²)/2

  • A=(π(6.5)²)/2

  • A=(42.25π)/2

  • A=66.36614481…

  • A=66.4 ft²

We can now conclude that the hardwood half of the table has an area of 66.4 square feet and we are finished!

 

Figure 14: How to find the area of a half circle with a diameter of 13 feet.

 

How to Find the Area of a Circle: Conclusion

Learning how to find the area of a circle or a half circle is an important and useful math skill.

You can find the area of a circle by using the formula A=πr² where r is the length of the circle’s radius.

If you only know the length of a circle’s diameter, you can simply divide it by two (since d=r/2) to find the value of its radius and then use the formula to find the circle’s area.

You can find the area of a half circle by using the formula A=(πr²)/2 where r is the length of the circle’s radius. This formula is derived from the regular area of a circle formula since the area of a half circle is equal to half the area of a regular circle with the same diameter.

Keep Learning:

How to Find Perimeter in 3 Easy Steps

Comment

How to Find Perimeter in 3 Easy Steps

How to Find Perimeter in 3 Easy Steps

Math Skills: Learn how to find the perimeter of a rectangle, square, triangle, parallelogram, and circle.

 

Free Step-by-Step Guide: How to Find the Perimeter of a Shape.

 

Are you ready to learn how to find perimeter of various shapes and figures?

This free guide will teach you all about perimeter and how to find the perimeter of several common shapes. You can use the quick links below to jump to any section of this guide:

In math, every student must learn how to find the perimeter of a two-dimensional shape. As long as you understand what perimeter means, you can easily find the perimeter of a shape by following a few easy steps.

For each example of how to find perimeter in this guide, we will use a simple 3-step method for finding perimeter that you can use to find the perimeter of any shape and to solve any math problem involving perimeter. As long as you can follow the three simple steps shared in this guide, you will always be able to find perimeter.

Let’s get started with a quick review of perimeter including some key vocabulary terms as well as an explanation of how to find perimeter before we move onto several specific examples.

How to Find Perimeter: Quick Review

Before you can learn how to find perimeter, you should be familiar with some important math concepts and vocabulary terms, which we will quick review here in this first section.

What is Perimeter?

Definition: In math, the perimeter of a shape is the total distance around the outer boundary of the shape.

Another way to describe the perimeter of a figure is the total measured length of the outline of the shape. Note that perimeter applies to two-dimensional shapes including triangles, rectangles, squares, etc.

For example, consider an equilateral triangle where each side has a length of 5 centimeters. To find the perimeter of the triangle, you would simply have to add up the lengths of all three sides as follows:

  • 5 + 5 + 5 = 15 cm

Therefore, we could say that the triangle has a perimeter of 15 cm.

We can also think of perimeter as taking all of the side lengths of a shape and laying them out as one long straight line. The total length of this line would be the perimeter of the figure. This idea is illustrated in Figure 01 below.

 

Figure 01: How to Find Perimeter Explained.

 

On a larger scale, we can imagine a rectangular shaped park with a paved sidewalk surrounding it. The perimeter of the park would be the total distance that you would have to walk to travel the complete outer distance of the park (i.e. how far you would have to walk along the sidewalk to go around the park and end up back where you started.)

We can say that perimeter is the total distance around the outer boundary of a two-dimensional shape or figure.

Also, note that, unlike area, perimeter is only concerned with the outer boundary of a figure (not the inside of a figure).

Figure 02 below further illustrates the idea that the perimeter of a figure is the length of its outer boundary.

 

Figure 02: Perimeter is the total distance around the outer boundary of a two-dimensional shape or figure.

 

Now that you understand the concept of perimeter, you are ready to learn how to find a perimeter of several common two-dimensional shapes including squares, rectangles, triangles, parallelograms, and circles.

How to Find the Perimeter of a Square

Example #1: Find the Perimeter of a Square

For our first example, we have to find the perimeter of a square with a side length of 8m, as shown in Figure 03 below.

 

Figure 03: How to Find the Perimeter of a Square

 

We can solve this first example of how to find the perimeter of a square (and all of the examples in this guide) by following the following three steps:

  • Step #1: Identify the Shape

  • Step #2: Identify all of the side lengths and add them together

  • Step #3: Determine the perimeter and use appropriate units of measurement

Let’s go ahead and apply these three steps to this first example of how to find perimeter of a square.

Step #1: Identify the Shape

Our first step is super easy. We know that the figure in question is a square with four sides that all have the same length (8m in this case).

Step #2: Identify all of the side lengths and add them together

We know that each side of the square has a length of 8m, so we can add them together as follows:

  • 8 + 8 + 8 + 8 = 32

Step #3: Determine the perimeter and use appropriate units of measurement

Finally, we can say that the length of the outer boundary of the figure is 32m and we can conclude that:

Final Answer: P=32m

Our procedure for solving this first example is illustrated in Figure 04 below.

 

Figure 04: How to find the perimeter of a square with a side length of 8m.

 

That’s all that there is to finding perimeter! In this example, we learned how to find a perimeter of a square, but the steps that we used can be used to find the perimeter of any two-dimensional shape, as you will see in the following examples.

How to Find the Perimeter of a Rectangle

Example #2: Find the Perimeter of a Rectangle

 

Figure 05: How to find the perimeter of a rectangle

 

In this next example, we will learn how to find the perimeter of a rectangle with a length of 12 ft and a width of 7 ft.

Just like the previous example, we can find the perimeter of this rectangle by using our three step strategy as follows:

Step #1: Identify the Shape

We already know that the shape in question is a rectangle that has four sides (two lengths and two widths). We also know that the opposite sides have equal measure, meaning that the two lengths equal 12 feet each and the two widths equal 7 feet each.

In many cases, all four sides of the figure will not be labeled, but you may find it helpful to go ahead and label them as shown in Figure 06 below:

 

Figure 06: How to Find Perimeter of a Rectangle: It can be helpful to label all four side lengths (opposite sides of a rectangle have congruent lengths).

 

Step #2: Identify all of the side lengths and add them together

Now that we have labeled all four side lengths, we can add them together as follows:

  • 12 + 12 + 7 + 7 = 38

Step #3: Determine the perimeter and use appropriate units of measurement

And now, for the final step, we can say that the perimeter of the rectangle is 38 feet, and we can conclude that:

Final Answer: P=38 ft

The diagram in Figure 07 below summarizes how we found the perimeter of the rectangle in this example.

 

Figure 07: The rectangle has a perimeter of 38 feet.

 

Now, let’s work through one more example of how to find perimeter of a rectangle.

Example #3: Find the Perimeter of a Rectangle

 

Figure 08: How to Find the Perimeter of a Rectangle

 

Notice that the rectangle whose perimeter we have to find in Figure 08 above has decimal side lengths.

This, however, will not change how we solve this problem and we can again use our three step strategy as follows:

Step #1: Identify the Shape

Since the shape in this example is a rectangle, we know that it has four sides, two of which have a length of 4.7 mm and two of which have a length of 8.1 mm.

Step #2: Identify all of the side lengths and add them together

Next, we can go ahead and find the sum of all four side lengths as follows:

  • 4.7 + 4.7 + 8.1 + 8.1 = 25.6

Step #3: Determine the perimeter and use appropriate units of measurement

Now we can conclude that the rectangle has a perimeter of 25.6 mm.

Final Answer: P=25.6 mm

The diagram in Figure 09 below illustrates how we found the perimeter of a rectangle with a length of 4.7 and a width of 8.1.

 

Figure 09: How to Find the Perimeter of a Rectangle in 3 Easy Steps

 

How to Find the Perimeter of a Triangle

In this next section, we will focus on two examples of how to find the perimeter of a triangle. Unlike the last two sections where we focus on squares and rectangles, triangles only have three sides and they do not necessarily have right angles. However, these differences will not prevent us from finding the perimeter of a triangle using our three step strategy, as you will see in the examples below.

Example #4: Find the Perimeter of a Triangle

 

Figure 10: How to Find the Perimeter of a Triangle Example

 

For this next example of how to find the perimeter of a triangle, we can again use our three step strategy to find the solution.

Step #1: Identify the Shape

In this example, we want to find the perimeter of a triangle (a three-sided shape). In this example, our triangle has side lengths of 30, 64, and 68.

Note that the triangle in this example, as shown in Figure 10 above, already has all three side lengths labeled for us.

Step #2: Identify all of the side lengths and add them together

For the second step, we have to add all three side lengths together as follows:

  • 30 + 64 + 68 = 162

Step #3: Determine the perimeter and use appropriate units of measurement

Finally, we can say that the perimeter of the triangle is 162 units and we can conclude that:

Final Answer: P=162

The entire process for how to find the perimeter of a triangle is shown in Figure 11 below.

 

Figure 11: How to Find the Perimeter of a Triangle Explained

 

Example #5: Find the Perimeter of a Triangle

 

Figure 12: How to Find Perimeter of a Triangle

 

Here is another example of finding the perimeter of a triangle (in this case, a right triangle). Let’s go ahead and use our three step strategy to find the solution.

Step #1: Identify the Shape

Even though this example features a right triangle, we still know the side lengths to be 3.6, 4.8, and 6, so we have enough information to move onto the next step.

Step #2: Identify all of the side lengths and add them together

Now, we can find the sum of all three sides of the triangle as follows:

  • 6 + 3.6 + 4.8 = 14.4

Step #3: Determine the perimeter and use appropriate units of measurement

From here, we know that the perimeter of the triangle is 14.4 units.

Final Answer: P=14.4

The steps for solving this problem on finding the perimeter of a triangle are in the diagram in Figure 13 below.

 

Figure 13: How to Find the Perimeter of a Triangle Explained

 

How to Find the Perimeter of a Parallelogram

Next, let’s take a look at an example of how to find the perimeter of a parallelogram.

Note that, in math, a parallelogram is a four-sided figure with two pairs of parallel sides where opposite sides are congruent in length. So, if you can find the perimeter of a rectangle or a square, then you can easily learn how to find the perimeter of a parallelogram.

Example #6: Find the Perimeter of a Parallelogram

 

Figure 14: How to Find the Perimeter of Parallelogram

 

Step #1: Identify the Shape

Notice that this example specifically asks us to find the perimeter of a parallelogram, so knowing the properties of parallelograms will be incredibly useful here (namely that the opposite sides of a parallelogram have congruent, or equal, lengths).

So, even though the parallelogram in the diagram shown in Figure 14 above only has two sides labeled, we actually have enough information to find the perimeter of the parallelogram.

Before we move onto the next step, let’s go ahead and label all four sides of the figure as shown in Figure 15 below.

 

Figure 15: Finding the Perimeter of a Parallelogram: Label all four side lengths.

 

Step #2: Identify all of the side lengths and add them together.

From here, we have a parallelogram with four side lengths: 40, 40, 54, and 54. For this second step to finding the perimeter of a parallelogram, we can find the sum of these four side lengths as follows:

  • 40 + 40 + 54 + 54 = 188

Step #3: Determine the perimeter and use appropriate units of measurement

Now that we have found the sum of the four side lengths of the parallelogram, we can say that the perimeter equals 188 units.

Final Answer: P=188

The complete three step process of how to find the area of a parallelogram is illustrated in Figure 16 below.

 

Figure 16: How to find the perimeter of a parallelogram explained.

 

Now that we have learned how to find the perimeter of a parallelogram, let’s move onto the final section of this guide on how to find the perimeter of shapes by looking at circles.

How to Find the Perimeter of a Circle

For this last section, we will focus on how to find a perimeter of a circle.

All of the shapes that we have previously covered in this guide (squares, rectangles, triangles, and parallelograms) had straight side lengths. However, circles do not have any sides at all, so how can we possibly find the perimeter of a circle?

 

Figure 17: How to Find Perimeter of a Circle Using the Circumference Formula

 

Remember that the concept of perimeter refers to the length of the outer boundary of a figure. And, when it comes to circles, the term that refers to its outer boundary is called its circumference.

So, anytime you are wondering how to find the perimeter of a circle, you should really be wondering how to find the circumference of that circle!

And, to find the circumference of a circle, we will have to use the circumference of a circle formula:

  • C=πd

In other words, the perimeter of a circle (i.e. the circumference of a circle) is equal to the product of π and its diameter.

With this in mind, let’s work through two examples of how to find the perimeter of a circle using the circumference formula.

*Note that in the examples below, we will use a calculator to make calculations using the exact value for π. However, you can approximate by as 3.14 to find estimated answers if you do not have access to a calculator will a π button.

Example #7: Find the Perimeter of a Circle

 

Figure 18: How to Find the Perimeter of the Circle Example

 

In the case of finding the perimeter of a circle, our three step strategy will not work.

In fact, you will rarely see questions that ask you to find the perimeter of a circle. Rather, they will more often require you to find the circumference of the circle, which is exactly what we will do to solve this problem.

Again, we will be using the formula C=πd where d is the length of the circle’s diameter, which, in this example, is 116 inches.

So, we can use the formula as follows:

  • C = π x d

  • C = π x 116

  • C = 364.424747…

  • C ≈ 364.4

For this example, we will round our answer to the nearest tenth and we can conclude that the perimeter of the circle is 364.4 inches.

Final Answer: P = 364.4 inches

 

Figure 19: How to Find Perimeter of a Circle Explained

 

Now, let’s move onto our very last perimeter example where you will gain more practice with how to find a perimeter of a circle.

Example #8: Find the Perimeter of a Circle

 

Figure 20: How to find the perimeter of a circle with a radius of 13.

 

We can solve this example of finding the perimeter of a circle the same way that we did the previously one.

However, notice that this example only gives us the length of the circle’s radius and not its diameter.

To find the length of the radius, we simply have to double the length of the given radius (13 m) as follows:

  • d = r x 2

  • d = 13 x 2

  • d = 26

Now that we know that the circle has a radius of 26m, we can use the circumference of a circle formula to find its perimeter as follows:

  • C = π x d

  • C = π x 26

  • C = 81.6814089…

  • C ≈ 81.7

Rounding our answer to the nearest tenth, we can conclude that the circle has a perimeter of approximately 81.7.

Final Answer: P = 81.7 m.

 

Figure 21: How to Find the Perimeter of a Circle Using the Circumference Formula.

 

Conclusion: How to Find Perimeter

In math, the perimeter of a shape is the total distance around the outer boundary of the shape. You can also think of perimeter as the measured distance along the outline of the shape.

In this guide on how to find perimeter, we worked through several examples of how to find the perimeter of a rectangle, a square, a triangle, and a parallelogram using the following three step strategy:

  • Step #1: Identify the Shape

  • Step #2: Identify all of the side lengths and add them together

  • Step #3: Determine the perimeter and use appropriate units of measurement

We also looked at the special case of how to find the perimeter of a circle, where we used the circumference formula, C = π x d, the find the length of the outer boundary of any circle.

Finding the perimeter of a shape is a relatively easy math skill that you can learn through practice and understanding the meaning of perimeter and the procedure for finding it will help you to solve problems inside and outside of the math classroom.

Keep Learning

How to Find the Area of a Parallelogram in 3 Easy Steps

Learn how to find the area of any parallelogram in this free step-by-step guide.

Search Tags: how to subtract fractions, subtracting fractions, how to subtract fractions with different denominators, fraction subtraction, subtracting fractions with unlike denominators, how do you subtract fractions?

Comment

How to Address an Envelope—Explained with Examples

How to Address an Envelope—Explained with Examples

How to Address and Envelope Step-by-Step

Your Quick Guide on How to Write the Address on an Envelope

 

Learn how to write an address on an envelope in 3 easy steps.

 

Knowing how to address an envelope is a valuable life skill that every person should learn how to do at some point.

Sending and receiving letters containing important information, financial documents, and notifications is a part of adult life and you will need to know how to write an address on an envelope correctly. Luckily, addressing an envelope is relatively easy to do and you can learn how very quickly.

This free Life Skills Guide on How to Write an Address on an Envelope will cover the following topics and examples:

Note that you do not have to follow this guide in order, and you can use the text links above to skip to any particular section that interests you.

Now, let’s start with a quick explanation of why letters and useful and why being able to properly address an envelope is an important life skill like knowing how to write a check.

 

How to Address an Envelope: Many couples still send physical thank you cards through the mail to individuals who attended their wedding. (Image: Mashup Math MJ)

 

What are Letters and Why are They Useful?

Communicating via letters sent in envelops has been done for hundreds of years and, even in today’s digital world, remains a useful and popular way of sending and exchanging information.

Today, letters have many uses such as sending someone a physical card to commemorate an event or to share condolences, important notifications and information, and legal and financial documents.

For example, the Internal Revenue Service (IRS), relies primarily on sending letters through the mail to communicate with and notify individuals. In fact, the IRS’ first point of contact with a customer will always be through the mail, since sending letters is a secure and traceable form of communication.

Since sending and receiving letters continues to be prevalent, learning how to address an envelope is an important life skill because you will certainly want to know that anything that you send—whether it be a birthday card with a check enclosed or your tax return documents—will reach its intended recipient.

How to Address and Envelope: Step-by-Step

 

How to Address and Envelope in 3 Easy Steps

 

Now you are ready to learn how to write an address on an envelope.

Note that there are three key steps to correctly addressing an envelope:

  • Return Address (Top-Left Corner)

  • Recipient’s Address (Center)

  • Stamp (Top-Right Corner)

Next, we will walk through each step of how to put the address on an envelope so it reaches its intended destination.

While it is not a requirement, we highly recommend that you use black or blue ink whenever you are addressing an envelope and always write clearly and legibly so that postal workers are not confused or unable to deliver your envelope.

Start with a Blank Envelope

Before you do anything, make sure that you are starting with a blank envelope that is appropriately sized to fit your letter or card.

Note that the standard white envelope for letters is 4.125 x 9.5 inches, but envelopes come in many shapes, sizes, and colors. Greeting cards typically come with an envelope to hold the card as well. No matter what type of envelope you are using, the process below will apply.

However, make sure that you are writing the address on the front side of the letter. The front side is totally blank and empty, while the back side has a flap/opening (see Figure 01 below for a visual reference).

Figure 01: How to Address an Envelope: Start with a blank envelope that is large enough to hold your letter, card, or documents.

 

Step One: Write the Return Address in the Top-Left Corner

The first step is to write the return address in the top-left corner of the envelope.

The return address is your address (i.e. you, the sender). Putting a return address on a letter serves two purposes:

  1. It lets the recipient know who the letter is from before they open it

  2. If the letter can’t be delivered for any reason, it will be returned to this address

For example, let’s say that our sample letter is being sent by Alexander Johnson who lives at the following address:

  • 135 Pine Street, Denver, CO 80203

In the top left-hand corner of our blank envelope, we will write the following as our return address:

  • Alexander Johnson

  • 135 Pine Street

  • Denver, CO 80203

Individuals who send letters often will sometimes have custom envelopes with the return address already printed on them while others will purchase stickers/labels with their return address printed on them. Either of these are exceptional alternatives to handwriting the return address.

Figure 02 below shows what our envelope will look like after writing the return address in the top left-hand corner.

Figure 02: How to Write the Address on an Envelope: Start by writing the return address at the top left-hand corner.

 

Step Two: Write the Address of the Recipient in the Center

The next step is to write the name and address of the recipient in the center of the envelope.

The recipient is the person or organization you are sending the envelope to.

Make sure that you write the name and address clearly and correctly and make sure that any numbers are legible and obvious to understand. If you make a mistake or if your handwriting is not readable, the letter will not make it to its intended destination.

In this example, we will be sending our letter to our friend Amanda Lee who lives at the following address:

  • 4917 River Avenue, Aspen, CO 81611

In the center of our envelope, in large font, we will write our recipient’s address as follows:

  • Amanda Lee

  • 4917 River Avenue

  • Aspen, CO 81611

Our letter after completing this second step is illustrated in Figure 03 below.

Figure 03: How to Address an Envelope: Clearly and legibly write the address of the recipient in the center of the envelope.

 

Step Three: Stamp and Seal Your Envelope

Now, all that you have to do is place a valid stamp in the top right-hand corner of the envelope and seal the flap on the backside.

Once you have completed this third and final step, your envelope is ready to be mailed.

There are several ways to mail a letter inside of a stamped envelope including:

  • Dropping the letter off at the post office

  • Placing the letter in an official USPS postal box

  • Leaving the letter in your mailbox for your mail carrier to receive

Figure 04 below shows what our envelope will look like after the final step has been completed.

Figure 04: How to Properly Address an Envelope

 

That’s all there is to it! You have just learned how to write the address in an envelope in a way that ensures that your letter or card will be delivered to the intended recipient. And, because you included a return address, your letter will be sent back to you in the event that it can not be delivered for any reason.

Figure 05 below shows what our completed envelope should look like. Once you have completed all three steps (return address, recipient’s address, and stamp), you are ready to send!

Figure 05: How to Address an Envelope: When your envelope looks like this, it is ready to send!

 

Example: How to Address an Envelope to a Family

Now that you know how to address an envelope to an individual, let’s take a look at a case where you want to address an envelope to an entire family.

For example, let’s say that Alexander Johnson who lives at 135 Pine Street, Denver, CO 80203 is sending invitations to a New Year’s Eve Party at his house and he wants to invite all six members of the Miller family.

Rather than sending each member their own invitation, he can send one invitation that is addressed to the entire family.

To address an envelope to a family, you will follow the same steps for addressing an envelope that we covered in the previous section, except that the name of the recipient will not be an individual or organization, but the name of the family (i.e. The Miller Family).

Let’s start by writing our return address in the top left-hand corner so that the family knows who the letter is from before opening it, as shown in Figure 06 below.

Figure 06: How to address a letter to a family: always include a return address.

 

Now, we are ready to write the address of the recipients, The Miller Family, at the center of the envelope.

Let’s say that the Miller family lives at 5242 Olive Tree Way, Evergreen, CO 80439. We would write the recipient’s address as:

  • The Miller Family

  • 5242 Olive Tree Way

  • Evergreen, CO 80439

By addressing the envelope this way, it implies that the card/invite inside of the envelope is meant for the entire family and that the message inside can be shared by all family members.

Finally, we just have to stamp our letter and we are all finished.

Figure 07 below shows how to address an envelope to a family as a completed letter ready to be sent!

Figure 07: How to Address an Envelope to a Family

 

That’s all there is to it. Once your envelope has been stamped and sealed, it is ready to send.

Example: How to Address an Envelope to a PO Box

This next example will teach you how to address an envelope to a PO Box.

A PO Box (or a Post Office Box) is a secure mailbox located at a post office or postal facility that can only be accessed by authorized individuals with a key. PO boxes are often used by individuals or businesses who want a private and secure location to receive mail.

The process for addressing an envelope to a PO Box is exactly the same as step-by-step process for addressing an envelope described in the first section of this guide, except that the address of the recipient will be a P.O. Box address instead of a street address.

For this example, let’s say that Alexander Johnson who lives at 135 Pine Street, Denver, CO 80203 is sending a letter with important financial documents to Gary Smith who works at Green Stripe Bank Headquarters.

Rather than having a traditional address, Green Stripe Bank has a PO Box Address.

To properly address an envelope to a PO Box, we first have to write our return address in the top left-hand corner as shown in Figure 08 below.

Figure 11: How to Address an Envelope to a PO Box: Start by writing the return address in the top left-hand corner.

 

Next, we are ready to write the PO Box address of the recipient, Gary Smith at Green Stripe Bank, at the center of the envelope.

Let’s say that the PO Box address of Green Stripe Bank is PO Box 247, Dallas, TX 75201:

  • Gary Smith

  • Green Stripe Bank

  • PO Box 247

  • Dallas, TX 75201

Notice that the address in this example has four lines, including the name of an individual (Gary Smith) and the business he is associated with (Green Stripe Bank). Note that some PO Box address will only include the name of the individual, while others will only include the name of the organization.

All that we have to do now is write this address on the center of our envelope and stamp our letter, as shown in Figure 09 below.

Figure 09: How to Address an Envelope to a PO Box Example.

 

Now we have successfully addressed an envelope to a PO box and we are ready to send.

 

How to Address an Envelope (Image: Mashup Math FP)

 

Conclusion: How to Put the Address on an Envelope

There are many reasons why you may have to send a letter, documents, or a card inside of an envelope through the mail and knowing how to address an envelope is an important life skill that you can easily learn.

This free guide taught you how to address an envelope in three easy steps:

  • Step One: Write the return address in the top left-hand corner

  • Step Two: Write the address of the recipient in the center of the envelope

  • Step Three: Place a valid stamp in the top right-hand corner

In addition to our broad explanation of how to write the address on an envelope, we also walked through two specific examples—how to address an envelope to a family and how to address an envelope to a PO box. Both of these examples have useful and practical applications, which is why we gave them a special focus.

In conclusion, by learning how to properly address and envelope, you are able to communicate through the mail in any way that you need to, and you can ensure that whatever you are sending—whether it be cards, letters, or important documents—reaches its intended destination as planned.

Keep Learning:

How to Write a Check in 6 Easy Steps

Knowing how to write a check is an important life skill that every person should know how to do. This free step-by-step guide will teach you everything you need to know about writing checks.

How to Write a Check—Explained with Examples

How to Write a Check—Explained with Examples

How to Write a Check Step-by-Step

Your Quick Guide on How to Write a Check for Any Reason

 

Learn how to Write a Check in 6 Simple Steps (Image: Mashup Math FP)

 

Knowing how to write a check is an important life skill that every person should know how to do.

While learning how to write a check can seem complicated, it’s actually a relatively simple process that you can learn in just a few minutes.

This short step-by-step guide on how to write a check will cover the following topics:

You can click on any of the text links above to jump to any topic or section of this guide, or you can read through each section order.

Are you ready to get started?

Why are Checks Useful?

We live in a digital world where online banking and money transfer apps are prevalent, yet knowing how to write a check is still a useful skill and physical checks are still useful for a variety of reasons.

 

Learn How to Write a Check (Image: Mashup Math MJ)

 

Since certain payment transactions can not be made using a credit/debit card or online, paying by check is often your safest option.

For example, if a landlord does not accept credit card or online payments for your monthly rent, then submitting a check payment would be your best option. If you pay with cash, you have no proof that you actually made the payment. However, if you pay with check, your bank can verify that the check was cashed and that you indeed made your payment.

In addition to proof of payment, paying by check offers additional security benefits that cash does not provide. Cash can be lost or stolen and, once cash is submitted, the payment can not be cancelled. Checks, on the other hand, can be cancelled.

Additionally, checks are extremely useful anytime you have to send a payment by mail. If your payment gets lost, you can always send a new check with no harm done. However, if you mail cash and the payment is lost, you are out of luck (and money!).

Also, many formal transactions require payment by check. Such transactions include making a down payment on a house, submitting a tax payment by mail, or paying rent to a landlord.

Finally, many older individuals are not comfortable with digital or online banking transactions and they rely on using checks to transfer and receive money or payments. Since checks are a familiar and trusted payment option for such individuals, it is highly beneficial that you are familiar with how to write a check.

So, whenever you can’t make a financial transaction digitally, it is usually safer to pay with a check than it is to use cash.

How to Write a Check: Step-by-Step

How to Write a Check: Start with a blank check that is linked to your personal checking account. (Image: Mashup Math FP)

 

Now that you know why checks are a safe and useful payment option, especially whenever digital payment options are not available or when you have to submit a payment by mail, it’s time to learn how to write a check.

Note that there are six different sections on a check that you must fill out:

  • Date

  • Recipient

  • Amount as a Number

  • Amount in Words

  • Memo

  • Signature

Below, we will show you how to complete all six sections and how to properly write a check. Note that these steps can be followed whenever you have to write a check for any reason!

For each step below, make sure you use blue or black ink and that you write using clear and legible handwriting.

Step One: Fill Out the Date

The first step to writing a check is to fill in the date section in the upper-right corner of your blank check. Make sure that you include the month, day, and year when you write the date.

In Figure 01 below, the check has been dated for July 4th, 2024.

Figure 01: How to Write Out a Check: Start by filling in the date at the upper-right corner.

 

Step Two: Write the Name of the Recipient

Next, you will see a blank line next to text that says PAY TO THE ORDER OF.

On this line is where you write the name of the recipient (i.e. the name of the person, business, or organization you are sending money to).

If you are sending money to another person, write their full first and last on this line.

If you are writing a check to a business or organization, write the name of the business or organization on this line. For example, if you are sending a check as a tax payment, you would write your check out to the Internal Revenue Service.

Note that only the person, business, or organization to whom the check is written out to can cash your check. If the check is lost or stolen, another person would not be able to cash the check.

In Figure 02 below, our check is being made out to a landlord named Alexander Johnson.

Figure 02: How to Write a Check The second step is to fill in the name of the person, business, or organization you are writing the check to.

 

Step Three: Write the Payment Amount as a Number

The third step is to fill in the box directly below the date, where you have to write in the numerical dollar amount that the check is for.

This amount should always include a decimal and the total number of cents. If the dollar amount is a whole number, you can use .00 to indicate that there are no cents (later on, we will show you how to write cents on a check).

In this example, we are writing a check for $900.00, as shown on our check in Figure 03 below.

Figure 03: How to Write a Check: Fill in the numerical dollar amount that the check is for in the box just below the date.

 

Step Four: Write the Payment Amount in Words

Next, directly below the line where you wrote the name of the recipient, you will see another blank line.

On this line, you will write the numerical payment amount in words.

In this example, our payment amount was $900.00. So, the payment amount in words would be:

  • $900.00 → Nine Hundred Dollars and Zero Cents

Figure 04 below shows how this fourth step was completed on our sample check.

Figure 04: How to Write Numbers in Words on a Check

 

Step Five: Write the Payment Amount in Words

Next, in the bottom left-hand corner of our check, you will see a blank line that that serves as the memo section of the check.

The memo section is where you can write a short description for what the check is for. Some examples of memos include:

  • Rent Payment for July

  • Happy Birthday or Congratulations! (for a Gift)

  • First Quarter Tax Payment

  • Landscaping

  • Babysitting

While this section is optional, we highly recommend writing something down as a reference for what your check was for the sake of keeping good financial records.

Since our sample check is being made out to our landlord for July’s rent payment, we will write July 2024 Rent in the memo section as shown in Figure 05 below.

Figure 05: How to Write Out a Check: Complete the memo section in the bottom-left corner.

 

Step Six: Sign the Check

The last thing that we need to do is sign the check on the signature line at the bottom-right corner.

In order for the check to be valid, you must sign your name on this line (the check can not be cashed without a valid signature).

Figure 06 below shows our example check with an authorized signature.

Figure 06: Your check is not valid until you sign it.

 

Once you have completed these six steps, your check is valid and ready to be used as a payment method.

Note that you must have the dollar amount that your check is written for available in whatever checking account the check is linked to, otherwise the check will bounce when the recipient tries to cash it and you will incur a penalty fee.

Figure 07 shows what our completed sample check to Alexander Johnson for $900.00 or July’s rent payment would look like.

Figure 07: How to Properly Write a Check

 

Example: How to Write a Check for 1000 Dollars

Now that you know how to properly write a check, let’s go through another example where we have to write 1000.00 on a check for a particular payment .

In this case, we will say that the check is for a quarterly estimated tax payment to the Internal Revenue Service for the first quarter of 2024.

Just as we did in the step-by-step guide to writing a check above, we will have to complete six sections of the check:

  • Step One: Write the Date

  • Step Two: Write the Name of the Recipient

  • Step Three: Write the Payment Amount as a Number

  • Step Four: Write the Payment Amount in Words

  • Step Five: Write the Memo

  • Step Six: Sign the Check

Let’s start off by completing the first two steps: the date and the recipient. For this example, the date will be April 1st, 2024 and the recipient will be the Internal Revenue Service.

Our check after completing steps one and two is shown in Figure 08 below:

Figure 08:How to Write a Check for 1000: The first step is to write the date and the name of the recipient. (Image: Mashup Math FP)

 

Writing any check, whether it’s for 1000 or 100,000, starts with writing the date in the top-right corner and the name of the recipient on the Pay to the Order Of line.

Next, we are ready to add a dollar amount to our check, which means that we are ready to complete steps three and four.

Start by writing 1,000.00 as a number in the box next to the $ sign on the right side of the check. Then, on the line below where you wrote the name of the recipient, write out $1000.00 in words as one thousand dollars and zero cents, as shown in Figure 09 below.

Figure 09: To write 1000.00 on a check, you have to write the dollar amount both as a number and in words.

 

Finally, the last two steps are to fill in the memo section and then to make the check valid by signing it in the bottom-right corner.

Since we said that this check was for making an estimated quarterly tax payment, we will put that as our memo and then sign the check, as shown in Figure 10 below.

Figure 10: How to Write 1000.00 on a Check Explained

 

Example: How to Write with Cents

In this next section, we will take a look at an example of writing a check with cents involved.

In the case of writing a check in cents, the six step process for writing a check described above is exactly the same:

  • Step One: Write the Date

  • Step Two: Write the Name of the Recipient

  • Step Three: Write the Payment Amount as a Number

  • Step Four: Write the Payment Amount in Words

  • Step Five: Write the Memo

  • Step Six: Sign the Check

For this example, we want to pay our dog groomer, Amanda Lee, using a personal check for a total of $78.26.

Notice that, unlike the last two examples, our payment amount does not end in .00. Rather, the payment amount includes cents.

Now, we will learn how to write a check with cents starting with the first two steps: writing the date and the name of the recipient on our check as shown in Figure 11 below.

Figure 11: How to Write Cents on a Check: Start by filling in the date and the name of the recipient. (Image: Mashup Math FP)

 

Now you are ready to write the amount as a number and in words.

When it comes to writing a check in cents, you have to first write the payment amount (with cents included) in the box next to the $ sign. In this example, our numerical payment amount is $78.26.

Once we have written the payment amount as a number on the check, we have to write it in words on the line directly below where you wrote the name of the recipient as follows:

  • $78.26 → Seventy-Eighty Dollars and Twenty-Six Cents

Figure 12 below illustrates how we wrote the payment amount in cents both as a number and in words on our check.

Figure 12: How to Write a Check with Cents

 

Finally, to finish writing a check with cents, you just have to complete the memo (this check is for dog grooming services) and validate the check by signing it.

These final steps are shown in Figure 13 below, which completes this tutorial on how to write a check in cents.

Figure 13: How to Write a Check in Cents Completed

 

How to Write a Void Check

The last section of this guide on writing checks is about void checks.

A void check is similar to a normal check, except that is has the word “VOID” printed or written boldly across the front of the check. By clearly marking a check as void, it prevents the check from being valid as banks will not allow it to be accepted as a payment or to withdraw money from your account for any reason.

Why would you ever want to write a void check?

Figure 14: How to Write a Void Check

 

While having to write a void check is uncommon, there are some useful reasons that for writing a void check that include:

  • Setting up Direct Deposit for Paychecks: Many employers will require you to submit a voided check to set up direct deposit of your paychecks (i.e. your paychecks deposit directly into your desired bank account on pay day). The voided check gives your employer your bank accounts routing information that is needed to set up direct deposit.

  • Auto-Pay for Recurring Bills: Sometimes recurring service providers (e.g. internet or cell phone contracts) require users to submit a void check in order to set up automatic payments where the amount owed is drawn from directly from your checking account each month.

  • Account Security and Verification: You may need to provide a void check as a security measure to verify your banking information when you are attempting to complete certain types of financial transactions such as loans.

 

How to Write a Void Check Explained (Image: Mashup Math FP)

 

How to Write a Void Check (Step-by-Step):

  1. Get a Blank Check: Start with a blank check that is linked to the checking account that you are dealing with. For example, if you are using a void check to set up direct deposit, make sure that the check is linked to the account that you want your paychecks to direct deposit to.

  2. Write “VOID” Across the Check: In blue or black ink, write out the word “VOID” in large capital letters across the front of the check. The word “VOID” should cover most of the surface of the check and it should be extremely obvious to any observer. Note that you do not need to fill out any sections of a void check.

  3. Identify Important Information: Make sure that the word void is not obscuring any important information that one would need from a void check—namely your name that is printed at the top-left corner of the check and the account numbers and routing information numbers at the very bottom of the check. If these numbers are unreadable, then you will likely have to submit another void check.

Writing the word "VOID" across the front of a blank check is an easy and effective way to give someone a check as a way of sharing important banking details such as your account number and routing number without worrying about any fraudulent or unauthorized access to your checking account.

 

How to Properly Write a Check (Image: Mashup Math via Getty)

 

Conclusion: How to Write a Check

While digital online payments and money transfers are extremely commonplace, checks remain a useful and secure option for making payments, especially through the mail or when digital payment options are not available.

In fact, knowing how to write a check remains a necessary life skill that everyone should learn. This guide shared a simple step-by-step process for how to write out a check to a person, company, or organization. We also covered specific examples of writing a check for $1,000.00 and writing a check with cents. Finally, we covered the uses of a void check and how to write a void check if necessary.

By learning how to write a check and how and when you should submit payments using a check, you are building skills that will allow you to make financial transactions that are secure and traceable, thus minimizing risk and giving you peace of mind.

Keep Learning:

How to Address an Envelope in 3 Easy Steps

Whether you are mailing invitations, letters, or important financial documents knowing how to properly address an envelope is an important life skill that everyone should learn.

How to Find Slope on a Graph in 3 Easy Steps

Comment

How to Find Slope on a Graph in 3 Easy Steps

How to Find Slope on a Graph

Step-by-Step Guide: How to Find a Slope on a Graph by Following 3 Simple Steps

 

Step-by-Step Guide: How to find slope on a graph explained.

 

In algebra, you will often be working with linear functions of the form y=mx+b where m represents the slope and b represents the y-intercept.

When it comes to dealing with these types of linear functions on the coordinate plane, you can find figure out the slope of the line simply by analyzing its graph. This particular skill will be the focus of the free step-by-step guide, where we will learn how to find slope on a graph using a simple 3 step strategy.

This free guide on How to Find a Slope on a Graph will teach you everything you need to know about finding the slope of a line on a graph and this skill can be used to solve any problem that requires you to find the slope of a linear function graphed on the coordinate plane.

This guide will cover the following topics/sections:

You can use the hyper-links above to jump to a particular section of this guide, or you can work through each section in order (this approach is highly recommended if you are learning this skill for the first time).

Are you ready to get started? Let’s begin with a quick review of slope.

 

Preview: In this guide, we will learn to use “rise over run” to find slope on a graph.

 

Quick Review—What is Slope?

Before we get into any examples of how to find a slope on a graph, it’s important that you understand the concept of slope and what it means.

Definition: The slope of a line refers to the direction and steepness of the line.

Slope is often expressed as a fraction where the numerator represents the vertical change (the change in y-position) and the denominator represents the horizontal change (the change in x-position). When a slope is a whole number, you can think of it as having a denominator of 1 (for example, a line with a slope of 4 actually has a slope of 4/1).

There are four types of slope:

  • Positive Slope ↗️: Lines that increase from left to right have a positive slope.

  • Negative Slope ↘️: Lines that decrease from left to right have a negative slope.

  • Zero Slope ↔️: Horizontal lines have a slope of zero.

  • Undefined Slope ↕️: Vertical lines have an undefined slope.

Since we will be dealing with finding slope on a graph in this guide, it is important that you are familiar with what these four kinds of slope look like. Before moving forward, take a close look Figure 01 below, which illustrates examples of these four kinds of slope.

 

Figure 01: There are four types of slope on a graph: positive, negative, zero, and undefined.

 

We often refer to slope in terms of “rise over run” where rise refers to the line’s vertical behavior and run refers to the line’s horizontal behavior.

In this guide, we will use “rise over run” to help us to find a slope on a graph.

So, how does “rise over run” work?

Let’s consider the graph in Figure 02 below.

 

Figure 02: How can we find the slope of the line y=2/3x+1 on the graph using rise over run?

 

First, we are given the graph of the line that represents the equation y=2/3x+1.

By looking at this graph, you can see that the line is increasing from left to right, so we know that the slope will be positive.

Also, notice that, in this case, we are given the equation of the line in y=mx+b form: y=2/3x+1, so we should already know that the slope will equal 2/3.

But, what if we just given the graph of the line without the equation? How then could we find the slope of the graph?

This is where rise over run comes into play. When you have a graph with at least two known points on the graph, you can use rise over run to “build a staircase” from one point to another to determine the slope of the line (i.e. find the fraction that represents the change in y-position over the change in x-position for the given line).

Figure 03 below illustrates how to use rise over run to build a staircase from point to point to find the slope of the line.

 

Figure 04: How to find slope of a line on a graph using rise over run.

 

Notice that our staircase consistently rises upwards two units and then runs 3 units to the right from point to point.

This tells us that the line has a slope of 2/3. And, since 2/3 can’t be simplified or reduced, we can conclude that the line on the graph has a slope of 2/3 (which is positive).

Note that not all slopes will be positive and it won’t always be the case that your resulting rise over run fraction can’t be simplified or reduced (we will see both occurrences in the examples ahead).

The key takeaways here are that:

  • There are four types of slope: positive, negative, zero, and undefined

  • Slope can be expressed as a fraction that represents “change in y” over “change in x”

  • We can rise over run to find the slope of a graph as long as we know at least two points on the graph

Now, let’s go ahead and work through some examples of how to find a slope on a graph using an easy 3 step strategy that utilizes rise over run.

 

Figure 05: Understanding the difference between positive slopes and negative slopes in reference to rise over run.

 

How to Find Slope on a Graph

Example #1: Find the Slope of the Graph

For the first example and all of the examples that follow, we will use the following 3-step strategy for how to find a slope on a graph:

  • Step #1: Select two coordinate points on the graph that have integer coordinates and plot them on the line clearly.

  • Step #2: Using rise over run, build a step that connects the two points to find the change in y and the change in x (i.e. the slope of the line).

  • Step #3: Express your answer as a fraction and simplify if possible.

Now, let’s go ahead and dive into this first practice problem where we are given a line and we are tasked with finding its slope.

 

Figure 06: Find the domain and range of the graph of y=x^2.

 

All that we are given is a line on the coordinate plane without any points or an equation. However, we can still determine the slope of the graph by applying our 3-steps as follows:

Step #1: Select two coordinate points on the graph that have integer coordinates and plot them on the line clearly.

To complete the first step, look for points where the graph intersects perfectly at a coordinate with integer coordinates (i.e. it crosses a point where four boxes meet). You can several options for this first example, but for this demonstration, we will choose the following points and plot them on the graph:

  • (-5,7) and (0,6)

In Figure 07 below, you can see how we plotted these two points on the line to complete Step #1.

 

Figure 07: How to Find Slope on a Graph: The first step is to find and plot two points on the line with integer coordinates.

 

Step #2: Using rise over run, build a step that connects the two points to find the change in y and the change in x (i.e. the slope of the line).

Now we are ready to apply rise over run to find the slope. Starting with the leftmost point, we have to build a step that will connect the two points.

Notice that this line is decreasing from left to right, which means that the line has a negative slope.

Whenever we have a negative slope like the one in this example, we will have to “rise down” when performing rise over run (i.e. move downwards vertically instead of upwards).

The process for completing Step #2 is shown in Figure 08 below.

 

Figure 08: Since this line has a negative slope (it decreases from left to right), our rise action was in a downwards vertical direction).

 

Using rise over run, we can see that this negative slope rises downwards 1 unit and to the right 5 units, so we can conclude that the slope is -1/5.

Step #3: Express your answer as a fraction and simplify if possible.

We now have a fraction that represents the slope of this line: m = -1/5.

Since this slope was negative, it needs to include the negative sign. Now, the last step is to check if the fraction -1/5 can be simplified or reduced. Since it can not be, we can conclude that:

Final Answer: The line has a slope of -1/5.

If we were to use this result to “continue the staircase,” we will see that rising down 1 unit and running to the right 5 units from any point on the line will land you on another point on the line (as shown in Figure 09 below).

 

Figure 09: The line has a slope of -1/5.

 

You can use the 3-step strategy that we used for Example #1 to solve any problem where you have to find slope on a graph without a given equation. Let’s gain more experience with the 3-steps by working through another practice problem.

Example #2: Find the Slope of the Graph

For our next example, we have to find the slope of a graph of a pretty steep line. Notice that this line is increasing from left to right, so the slope will be positive.

 

Figure 10: How to Find the Slope of a Line on a Graph

 

Step #1: Select two coordinate points on the graph that have integer coordinates and plot them on the line clearly.

For the first step, let’s go ahead and find two points with integer coordinates that the line passes through. For this practice problem, we will choose the following points on the line:

  • (0,-5) and (2,7)

Then go ahead and plot these points on the graph as shown in Figure 12 below:

 

Figure 12: To find the slope on a graph, start by plotting two points on the line that have integer coordinates.

 

Now that we have plotted our two points on the graph, we are ready for the next step.

Step #2: Using rise over run, build a step that connects the two points to find the change in y and the change in x (i.e. the slope of the line).

Next, we have to use rise over run and build a step that connects the two points so we can determine the slope.

Again, since this line is increasing from left to right, we know that the slope will be positive and that, unlike the last example where the slope was negative, we will have to “rise up” when performing rise over run.

Figure 13 below shows how we can use rise over run to get from (0,-5) to (2,7). You can see that the slope, in this case, is 12/2.

 

Figure 13: In this case, rise over run gives us a slope of 12/2, but can it be simplified?

 

After completing Step #2, we can see that the rise was 12 and the run was 2, so we conclude that our slope is: m = 12/2.

Is this our final answer? Let’s perform the third and final step to find out.

Step #3: Express your answer as a fraction and simplify if possible.

Although we have an answer in the form of a fraction, m=12/2, we should know that the fraction 12/2 can be simplified as 6/1 (or just 6).

To say that this line has a slope of 12/2 is not incorrect, but slopes of lines are typically expressed in reduced form.

If we apply our new slope of 6/1 to the point (0,-5) and build our staircase, we will see that the point (1,1) is also on the graph. And, if we continue from that point, we will end up at (2,7), which we know is also a point on the line.

The equivalent relationship between m=12/2 and m=6 is shown in Figure 14 below:

 

Figure 14: The slope 12/2 can be simplified as 6/1 or just 6.

 

Final Answer: The line has a slope of 6.

Are you starting to get the hang of it?

Let’s go ahead and take a look at another example.

Example #3: Find the Slope of the Graph

In this third example, let’s take a look at a horizontal line.

 

Figure 15: How to Find Slope on a Graph: Horizontal Lines

 

In our review of slope at the start of this guide, we shared that there are four kinds of slope: positive, negative, zero, and undefined.

In the case of horizontal lines, like the line shown on the graph in Figure 15 above, the slope will always be zero.

While we already know that the slope of this line is 0, let’s apply our 3-step method to see if this is actually true.

Step #1: Select two coordinate points on the graph that have integer coordinates and plot them on the line clearly.

You can pick any two points on the line. We will go with:

  • (-4,6) and (5,6)

These points have been plotted on the graph in Figure 16 below:

 

Figure 16: How to find a slope on a graph: zero slope

 

Step #2: Using rise over run, build a step that connects the two points to find the change in y and the change in x (i.e. the slope of the line).

Notice that we can not rise or nor rise down since the slope of this line is neither negative nor positive.

Figure 17 below shows how we can use rise over run to get from (-4,6) to (5,6). Since the rise is 0 and the run is 6, we can say that the line has a slope of 0/6.

 

Figure 17: Horizontal lines have a slope of zero.

 

Step #3: Express your answer as a fraction and simplify if possible.

After completing Step #2, we know that the rise over run is 0/9, and we also know that 0 divided by 9 is just equal to 0 and we can conclude that:

Final Answer: The line has a slope of 0.

Conclusion: How to Find a Slope on a Graph

The slope of a line refers to the direction and steepness of that line and there are four types of slopes:

  • Positive Slope ↗️

  • Negative Slope ↘️

  • Zero Slope ↔️

  • Undefined Slope ↕️

You can find the slope on a graph of a line by using the rise over run approach and by following the following 3-step strategy:

  • Step #1: Select two coordinate points on the graph that have integer coordinates and plot them on the line clearly.

  • Step #2: Using rise over run, build a step that connects the two points to find the change in y and the change in x (i.e. the slope of the line).

  • Step #3: Express your answer as a fraction and simplify if possible.

You can use these 3 steps to find the slope of any line on a graph, so make sure that you are comfortable using them before moving on. If you feel like you need more help, we recommend going back and working through the practice problems again!

Keep Learning:

How to Find Slope Using the Slope Formula

Your simple step-by-step guide to the formula for slope and how to use it to solve problems.

Comment