How to Find the Area of a Pentagon in 3 Easy Steps

Math Skill: How to Find the Area of a Pentagon Using an Easy 3-Step Process

The pentagon is a simple yet unique shape with fascinating mathematical properties that apply to geometry, nature, architecture, and even religion.

In the case of studying pentagons in geometry, it is important to know the key characteristics of pentagons—namely that a Pentagon is a regular polygon with 5 sides and 5 interior angles. The area of a pentagon is the internal space within the region enclosed by its five side. The size of the area of a pentagon depends on its shape and size (larger pentagons will have larger areas). Note that area, in the case of two-dimensional shapes, is always expressed in square units (or units squared).

(Looking for an area of a pentagon calculator? Click here to access our free Pentagon Area Calculator)

This short guide on how to find the area of a pentagon will teach you the following skills:

• What is the area of a pentagon?

• What is the formula for the area of a pentagon?

• How to find the area of a pentagon in 3 easy steps

• Calculating area of a pentagon examples (step-by-step)

• Free Area of a Pentagon Calculator

What is the Area of a Pentagon?

The area of a polygon—including pentagons—refers to the measure of the region inside of the boundary created by all of the sides. The area of a pentagon is calculated by dividing it into several simpler shapes and finding the sum of all of their individual areas. Generally speaking, the area of a pentagon is measured and expressed in square units, such as square meters or square feet.

You can easily find a pentagon’s area using the formula for the area of a pentagon. This standard formula can be used to find the area of any regular pentagon (a pentagon that with five sides that all have the same length).

Note that all of the pentagons in this guide are regular pentagons.

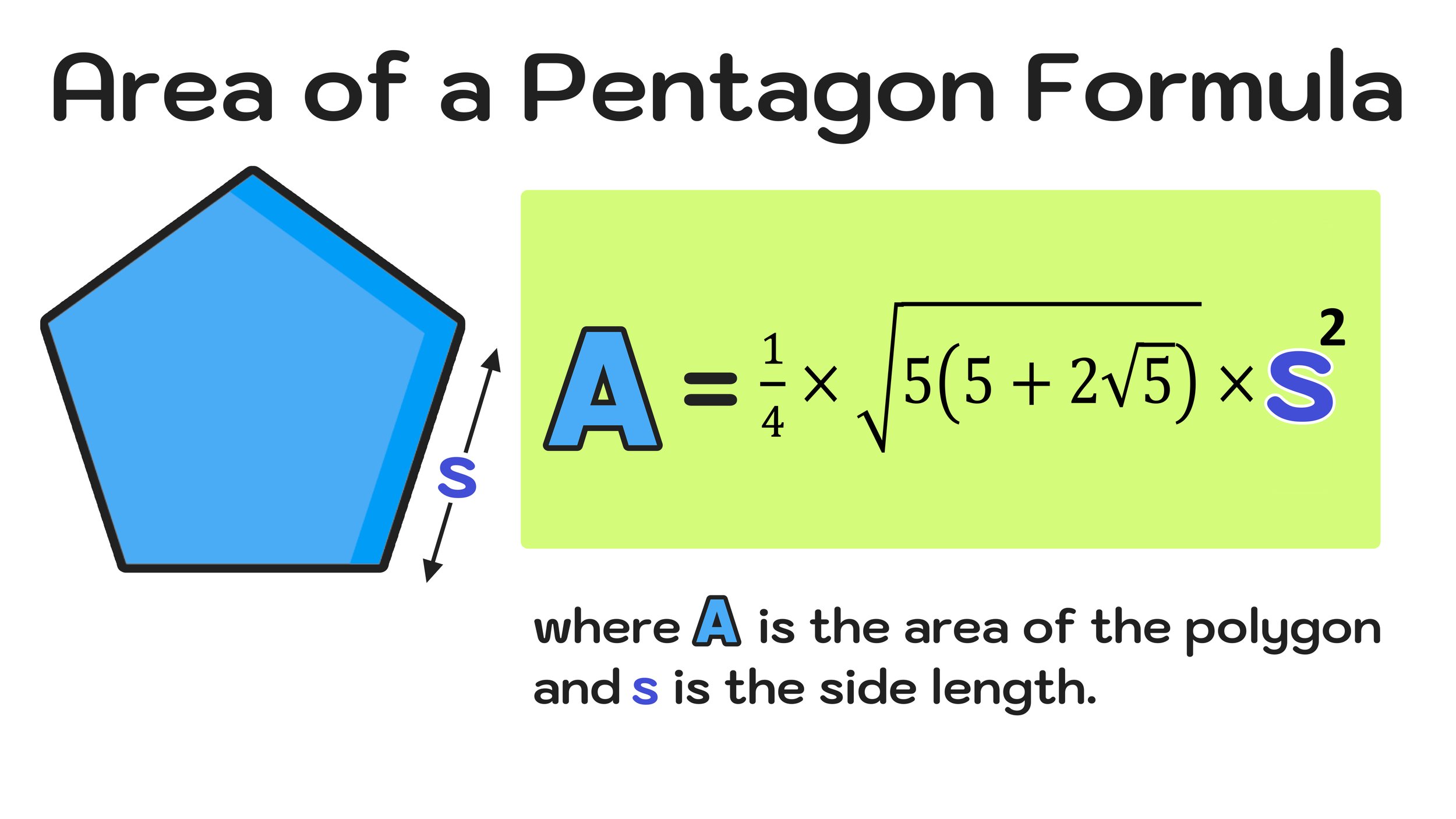
What is the Area of a Pentagon Formula?

You can calculate the area of a pentagon by using the formula for the area of a pentagon: A=1/4 x √(5(5+2√5) x s^2, where A equals the area of the pentagon and s equals the length of its sides.

How to Find the Area of a Pentagon in 3 Easy Steps

Being able to calculate the area of a pentagon is an important math skill that you can easily learn by using the following 3-step process for finding the area of a pentagon:

• Step One: Identify the value of s, the side length of the pentagon

• Step Two: Plug s into the area of a pentagon formula A=1/4 x √(5(5+2√5) x s^2 and solve for A

• Step Three: Express your answer using square units

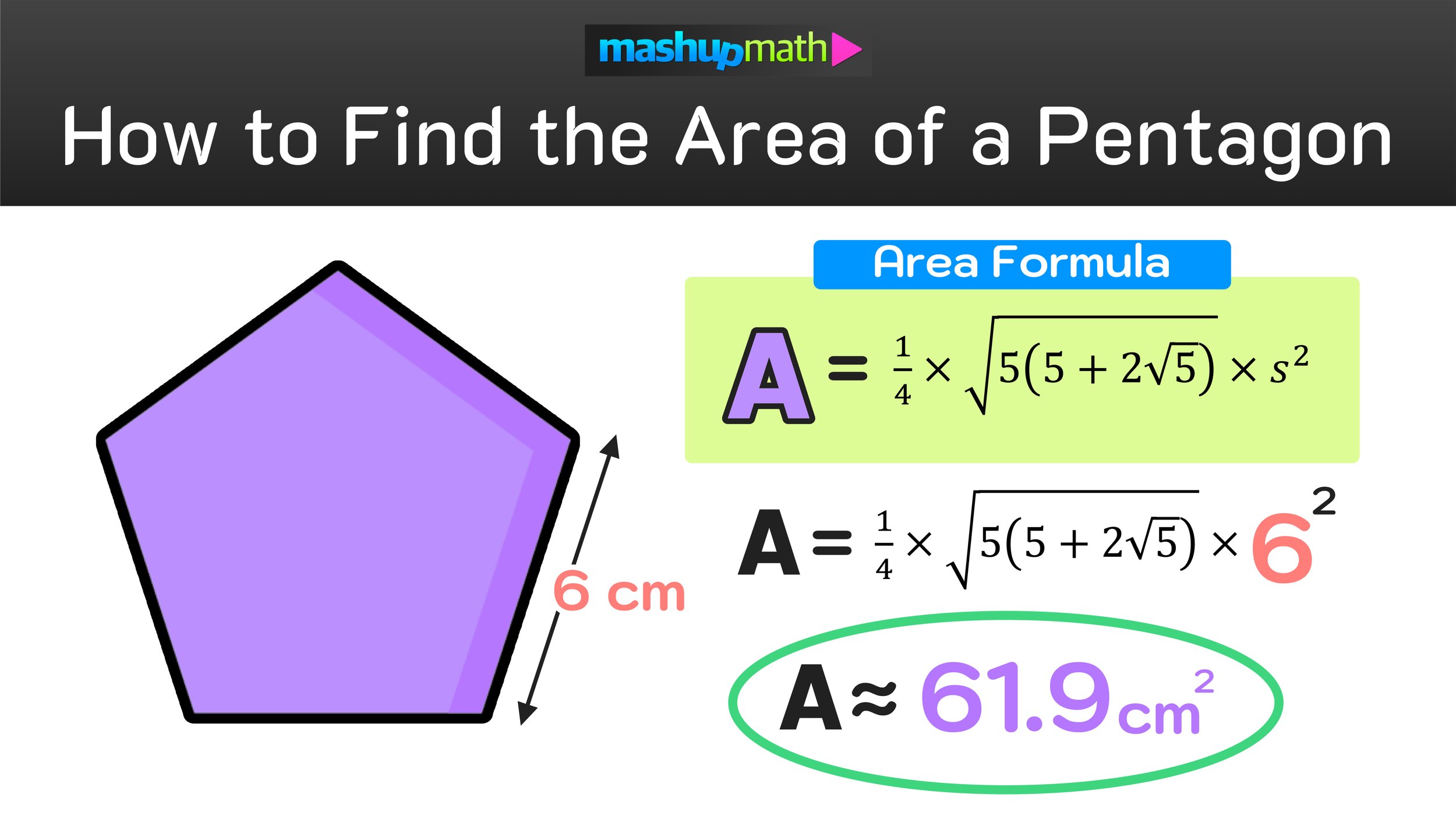
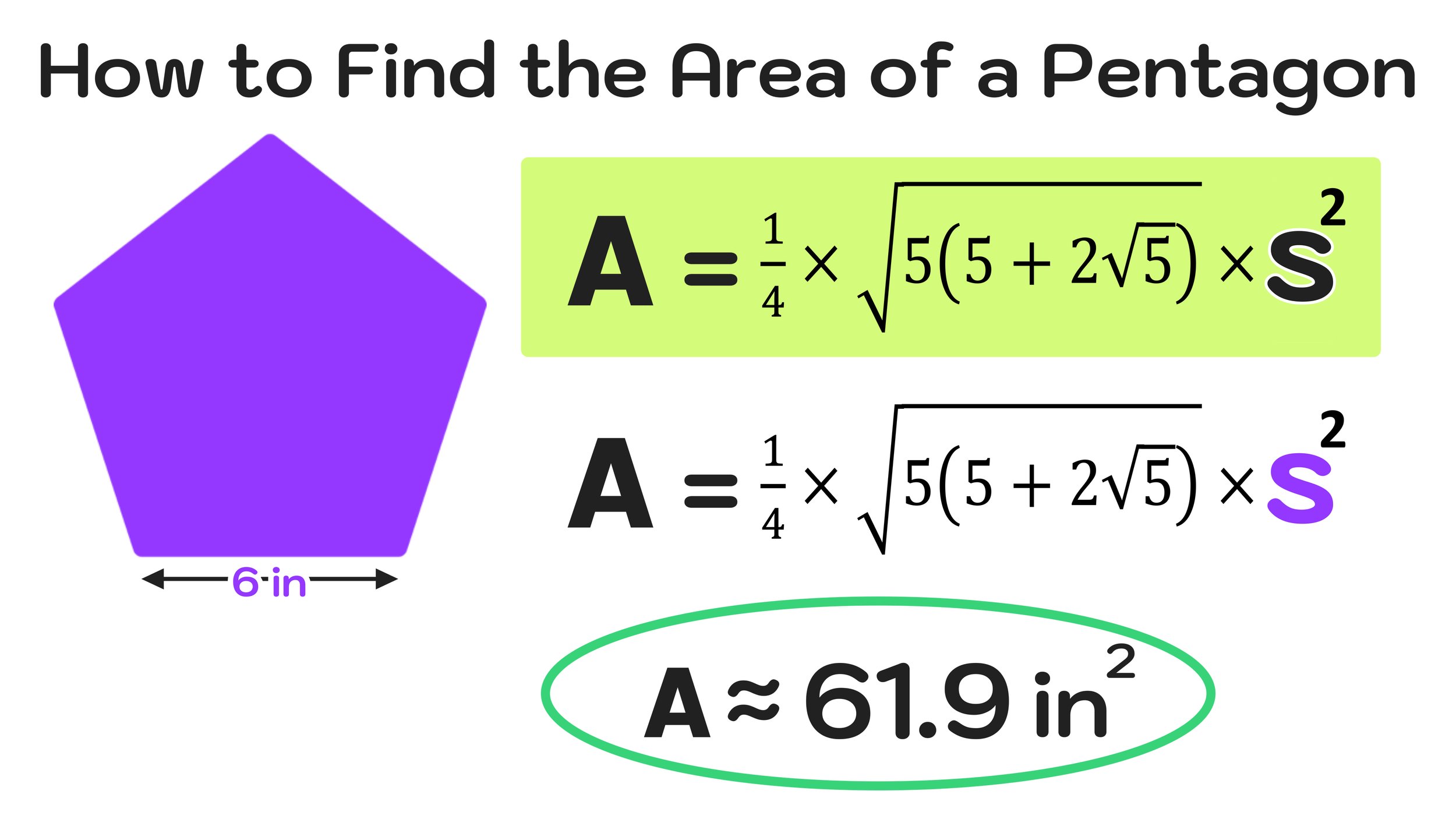
For example, you could calculate the area of a pentagon with a side length of 6 inches by inputting s=6 into the formula for the area of a pentagon and solving for A as shown in Figure 03 below.

Step One: Identify the value of s, the side length of the pentagon

In this example, s=6

Step Two: Plug s into the area of a pentagon formula A=1/4 x √(5(5+2√5) x s^2 and solve for A

Next, substitute s=6 into the area of a pentagon formula as follows:

• A=1/4 x √(5(5+2√5) x s^2 → A=1/4 x √(5(5+2√5) x 6^2 ≈ 61.93719

Step Three: Express your answer using square units

The final step for finding the area of a pentagon with a side length of 6 inches is to express the area in terms of square units.

Final Answer: The area of a pentagon with a side length of 6 inches is approximately 61.9 square inches.

Once you learn how to apply this 3-step process for finding the area of a pentagon using the formula for the area of a pentagon, you will be able to apply it when solving any future math problem that requires you to find a pentagon’s area, no matter its size.

To give you some more experience applying the three steps for figuring out the area of a pentagon, let’s move onto two more example problems.

How to Find the Area of a Hexagon Examples

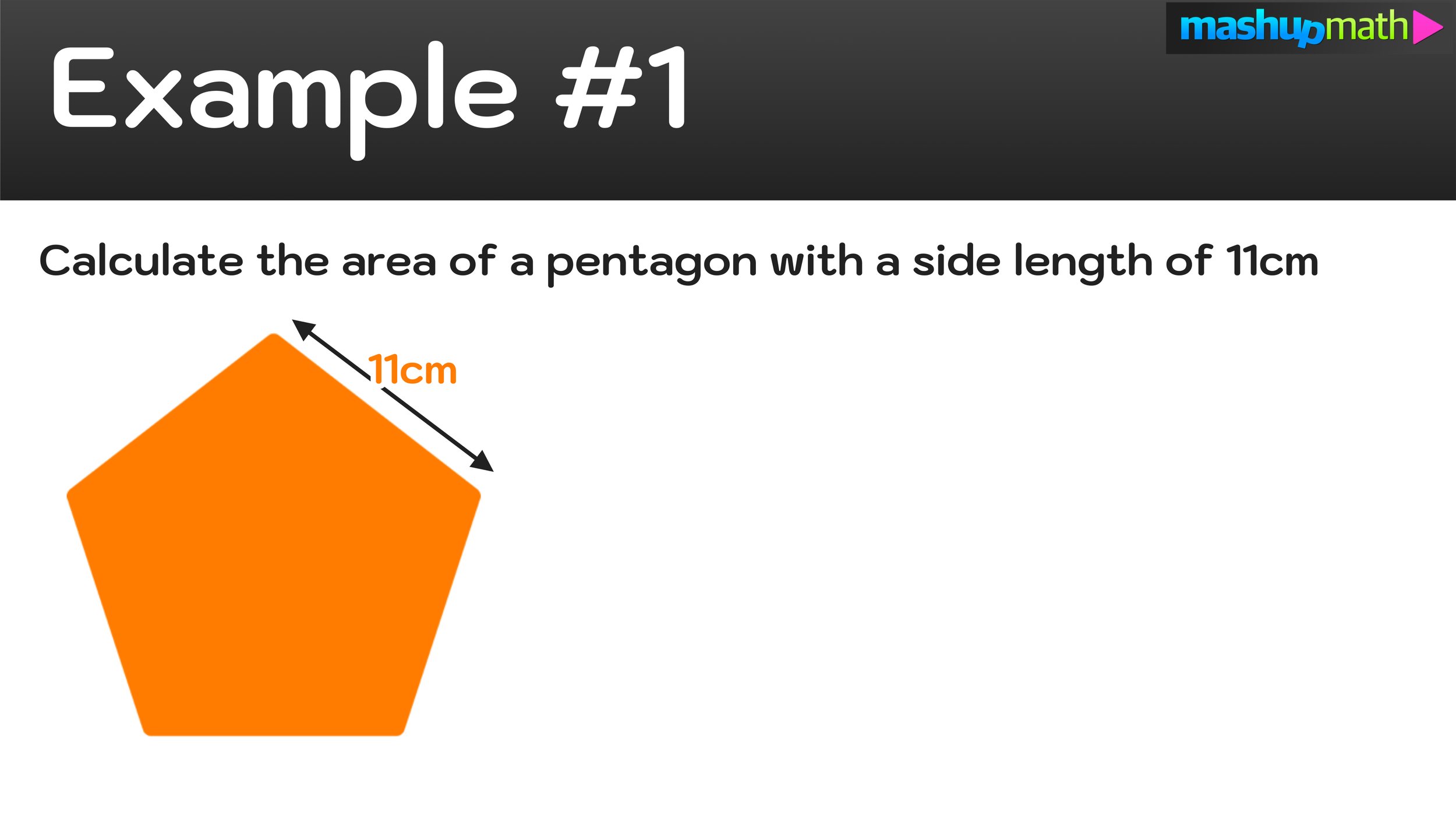
Example #1: Find the area of a regular pentagon with a side length of 11cm.

To find the area of a pentagon when s=11, you can easily use the three step method shown in the previous section of this guide.

Step One: Identify the value of s, the side length of the pentagon

In this example, the side length of the pentagon is 11cm, so we can say that s=11

Step Two: Plug s into the area of a pentagon formula A=1/4 x √(5(5+2√5) x s^2 and solve for A

For the second step, plug s=11 into the area of a pentagon formula as follows:

• A=1/4 x √(5(5+2√5) x s^2 → A=1/4 x √(5(5+2√5) x 11^2 ≈ 208.17777

Step Three: Express your answer using square units

Now you are ready to complete the problem. The last step is to express the area of the pentagon using square units.

Final Answer: The area of a pentagon with a side length of 11 centimeters is approximately 209.2 square centimeters

How to Find the Area of a Hexagon: Example #2: Find the area of a pentagon with a side length of 20.25 feet.

Just like the first example, you can solve this problem by following the three steps:

Step One: Identify the value of s, the side length of the pentagon

The side length of the pentagon in Example #2 is 20.25, so s=20.25

Step Two: Plug s into the area of a pentagon formula A=1/4 x √(5(5+2√5) x s^2 and solve for A

Next, input s=20.25 into the formula for the area of a pentagon:

• A=1/4 x √(5(5+2√5) x s^2 → A=1/4 x √(5(5+2√5) x 20.25^2 ≈ 705.50326

Step Three: Express your answer using square units

Finally, express the area of the pentagon using square units.

Final Answer: The area of a pentagon with a side length of 20.25 feet is approximately 705.5 ft^2 (or 705.5 square feet)

Area of a Pentagon Calculator

Use our Free Area of a Pentagon Calculator to Make Instant Calculations

Looking for way to instantly calculate the area of a pentagon without making manual calculations? If so, check out our free Area of a Pentagon Calculator, which is a useful and easy-to-use tool for quickly finding the area of a regular pentagon with side length s. You can also use the free calculator to check your work to make sure that any manual calculations that have made are correct.

→ Click Here to Access a Free Area of a Pentagon Calculator

Conclusion: How to Find the Area of a Hexagon

To find the area of a pentagon with side length s, you can use the area of a pentagon formula A=1/4 x √(5(5+2√5) x s^2², where A is the area of the pentagon and s is the side length.

The area of a pentagon formula can be used to find the area of any regular pentagon.

You can calculate the area of a regular pentagon by using the following 3-step method:

• Step One: Identify the value of s, the side length of the pentagon

• Step Two: Plug s into the area of a pentagon formula A=1/4 x √(5(5+2√5) x s^2 and solve for A

• Step Three: Express your answer using square units

Keep Learning:

• Geometric Shapes—Complete List and Properties

• The Platonic Solids Explained

• How to Find the Area of a Hexagon

• How to Find the Area of an Octagon

• How to Find the Area of a Parallelogram

• How to Find the Area of a Semicircle

More Math Resources You Will Love:

Search Tags: area of a pentagon, how to find the area of a pentagon, formula for the area of a pentagon, area of a pentagon calculator, area of a pentagon formula, the formula for the area of a pentagon, area of a regular pentagon, how to find the area of a pentagon, the area of a regular pentagon