What are Vertical Angles?
Your simple guide to Vertical Angles, Congruence, and the Vertical Angles Theorem
When studying mathematics—namely the field of Geometry—it is incredibly important to understand the properties of angles and angle relationships. One of the most common angle relationships that you will come across are vertical angles, or angles that are directly opposite each other.
In this short guide, we will explore and answer the questions:
What are vertical angles?
Are vertical angles congruent?
What is the Vertical Angles Theorem?
Once you learn the answer to these three questions, you will be able to understand the properties of vertical angles and solve math problems that involve vertical angles. You will also be able to identify an example of a vertical angle given a diagram (this guide includes three vertical angles examples and practice problems at the end).
What are vertical angles?
In math, you often have to be able to classify angles and angle relationships that are formed by two intersecting lines.
Vertical angles are the pairs of angles that are opposite (or directly across from) each other that are made by two intersecting lines.
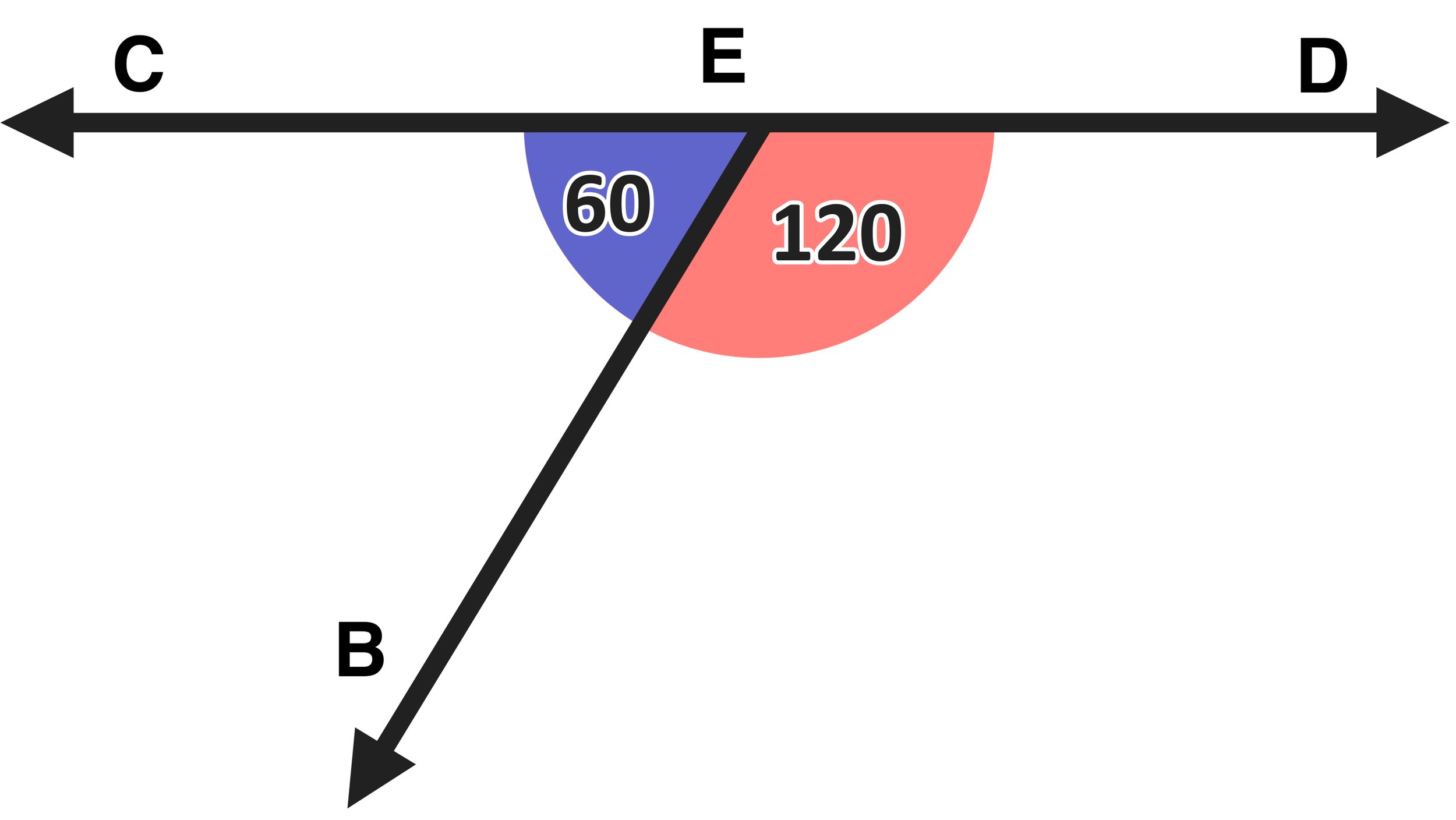
Take a look at the two intersecting lines shown in Figure 1 below. Notice that there are four total angles: ∠AEC, ∠DEA, ∠DEB, and ∠CEB
Figure 01
Remember that vertical angles are the pairs of angles that are opposite (or directly across from) each other. Whenever you have two intersecting lines, there will be two pairs of vertical angles. Let’s take a look at the first pair (shown in Figure 02 below): ∠CEB and ∠DEA are vertical angles.
Figure 02: What are vertical angles? ∠CEB and ∠DEA are vertical angles because they opposite each other.
Notice that ∠CEB and ∠DEA are opposite each other, which means that they are vertical angles.
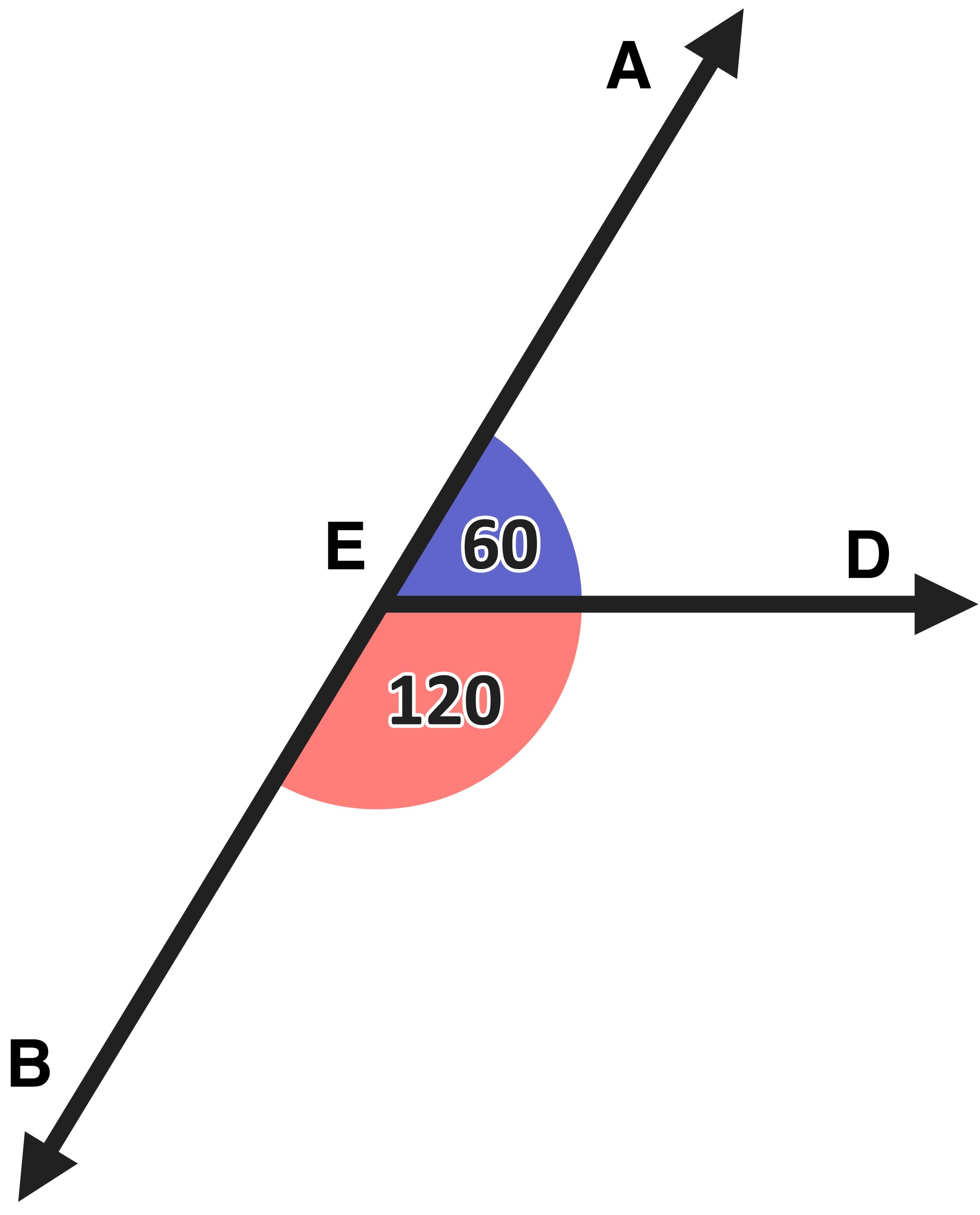
Now, let’s look at the second pair of vertical angles (shown in Figure 03 below): ∠AEC and ∠DEB are vertical angles.
Figure 03: What are vertical angles? ∠AEC and ∠DEB are vertical angles because they opposite each other.
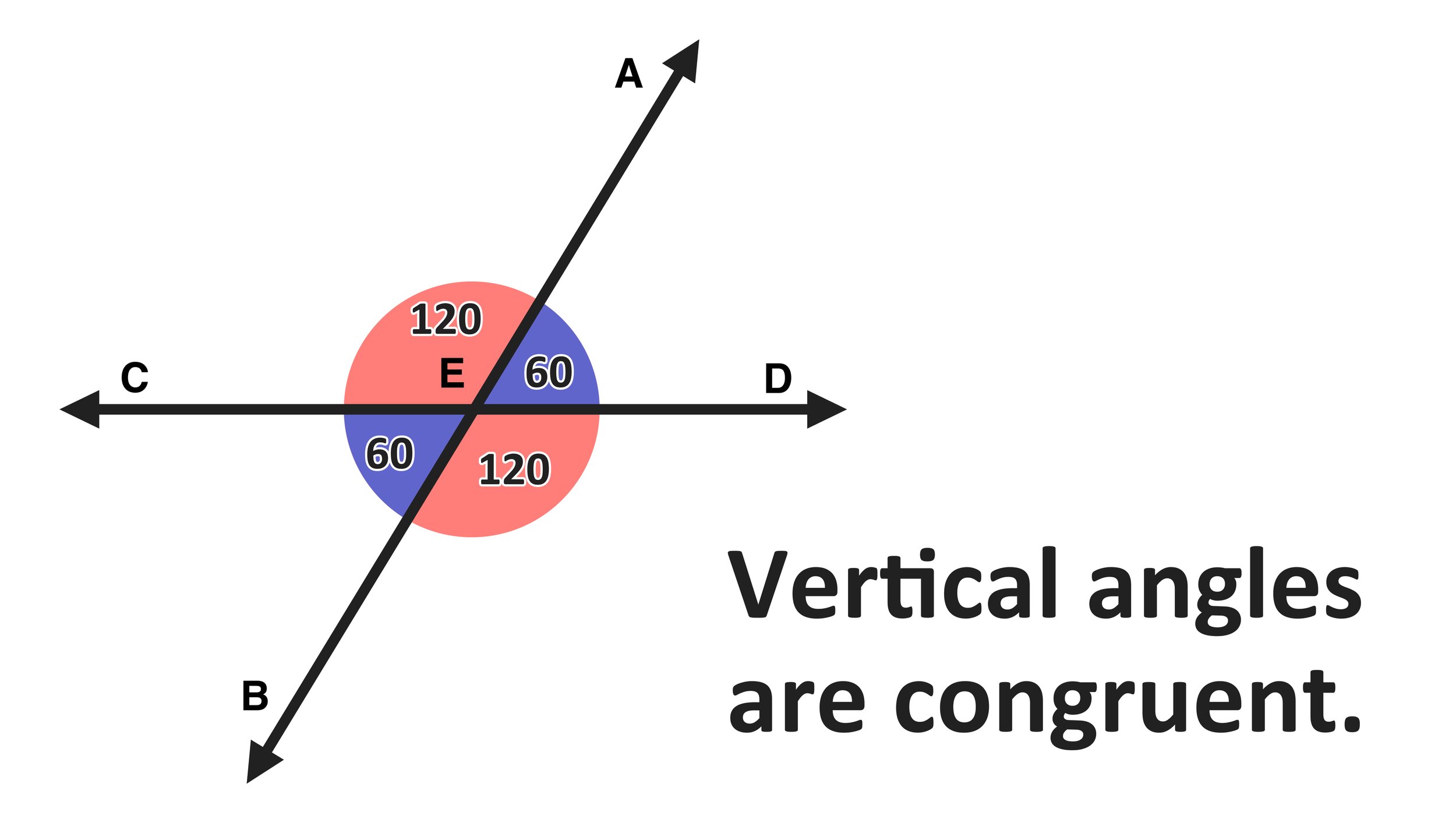
Finally, you can look at Figure 04, which shows color-codes both pairs of vertical angles and you can conclude that vertical angles are the pairs of angles that are opposite each other when two lines intersect.
Figure 04: Example of a vertical angle diagram.
Now that we’ve answered What are Vertical Angles?, we can move onto the next question.
Are vertical angles congruent?
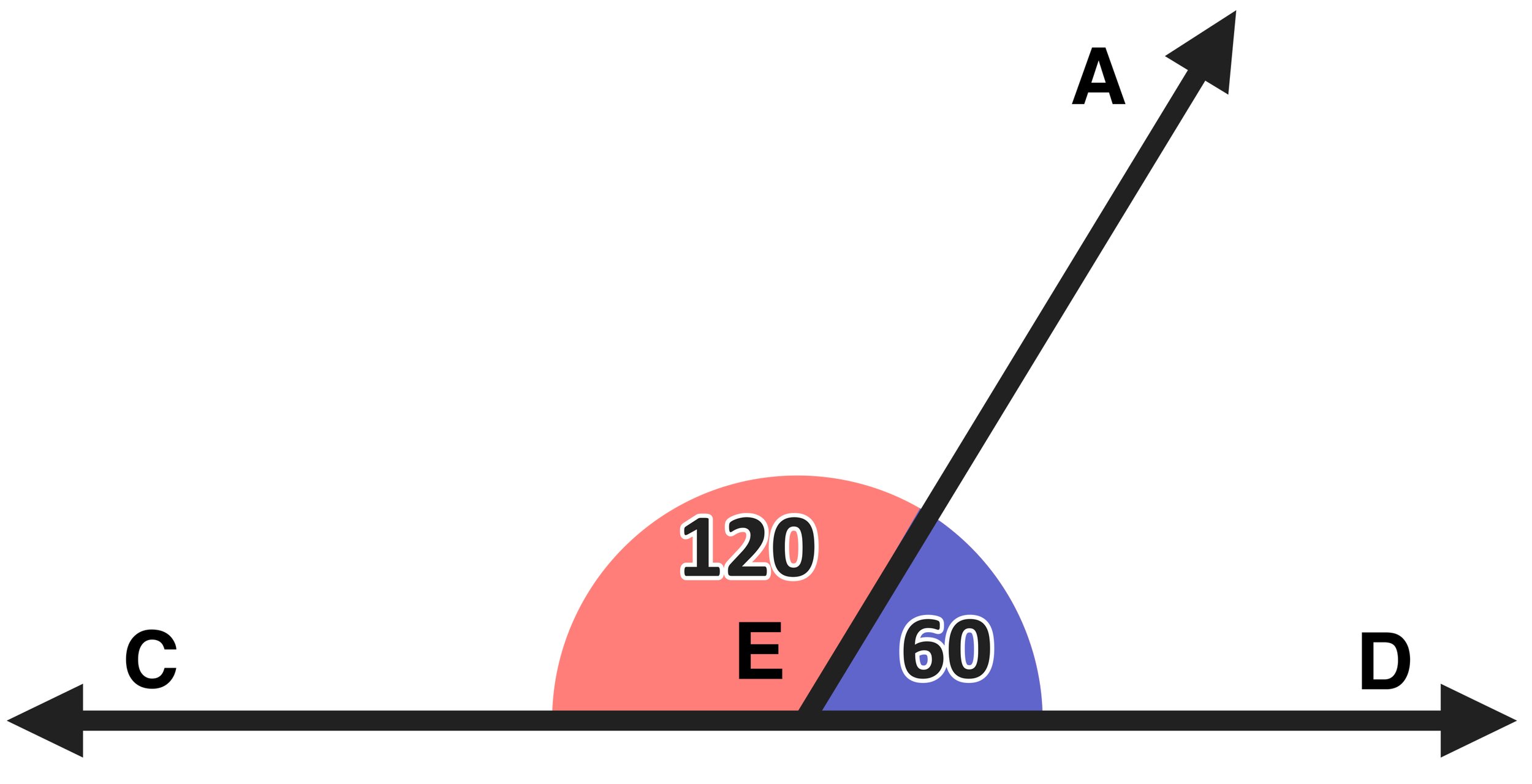
We can build upon the previous section to determine if vertical angles are congruent or not. First, take a look at Figure 05 below.
Answer: Vertical Angles are congruent.
Let’s explore why this is true. We can think of Figure 05 as the same graphic shown in Figure 04, but with a portion removed so that there are no longer any vertical angles.
Notice that the lines are slightly different as there are only two angles shown: ∠AEC and ∠DEA
Figure 05: Linear Pair (Supplementary Angles)
Since ∠AEC and ∠DEA combine to form a straight line, they are supplementary angles, which form a linear pair, which means that they will have a sum of 180. This is true for any linear pair, so any time that you add the salmon-colored angle to the purple-colored angle, the result will be 180.
In this case, let’s say that ∠AEC=120 and ∠DEA=60. Again, 120 + 60 = 180.
Figure 06: ∠AEC and∠DEA are not vertical. They are a linear pair.
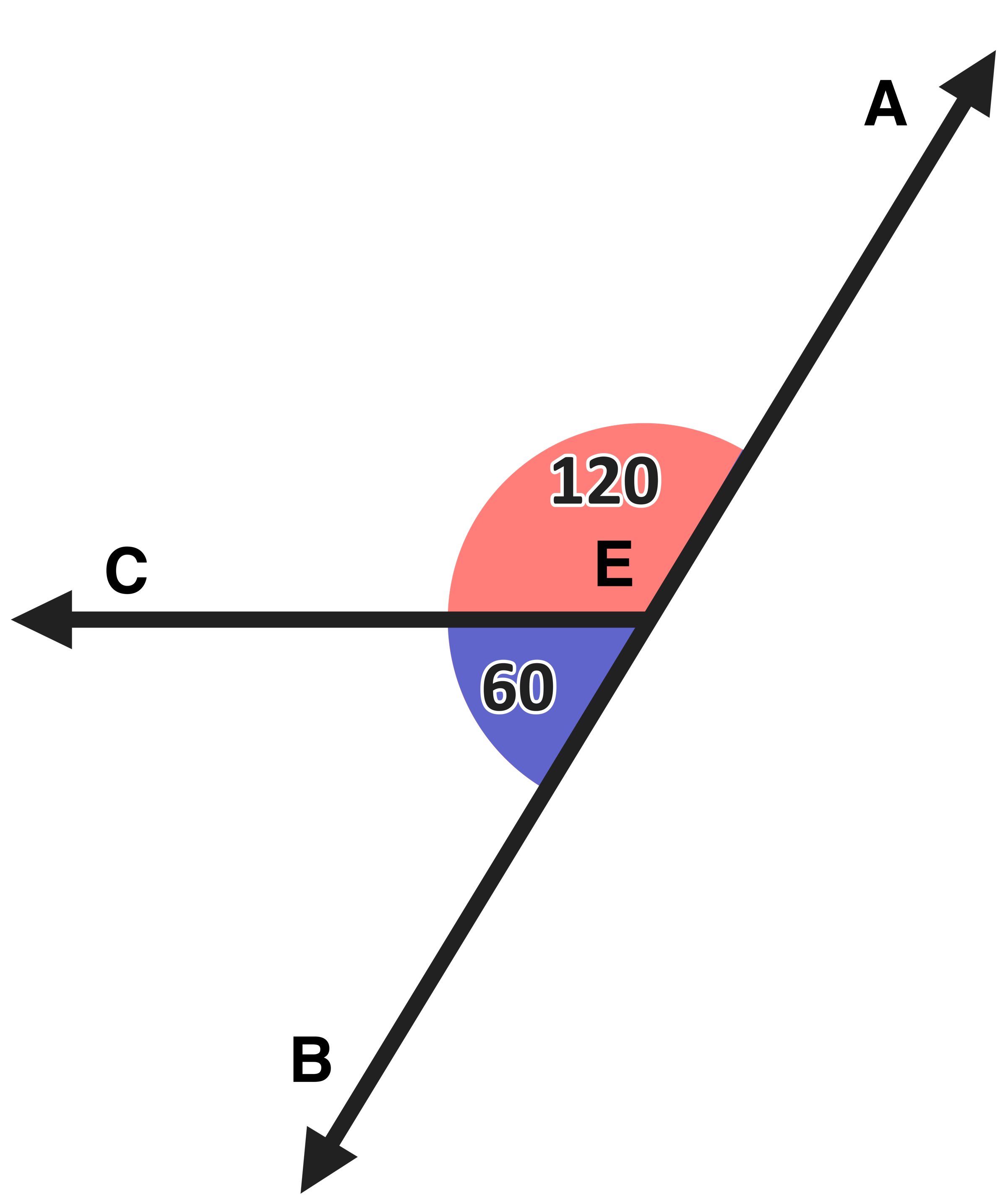
With this knowledge in mind, let’s look at the original image the two intersecting lines again, except this time labeling ∠AEC=120 and ∠DEA=60.
Figure 07
Knowing that ∠AEC=120 and ∠DEA=60 is enough to determine that values of ∠CEB and ∠DEB by applying the supplemental angles theorem, which states that any two adjacent angles that form a straight line must have a sum of 180 degrees.
If we overlap these four figures on top of each other (as shown in Figure 08 below), what do you notice?
Figure 08: Are vertical angles congruent? Vertical angles are always congruent, meaning that they always have the same degree measure.
The two pairs of vertical angles both have the same measure.
∠AEC and ∠DEB are vertical angles and they both equal 120 (they are both salmon-colored)
∠CEB and ∠DEA are vertical angles and they both equal 60 (they are both purple-colored)
∠AEC and ∠DEA are a linear pair and they combine to equal 180 (salmon-colored and purple-colored combo)
CEB and ∠DEB are a linear pair and they combine to equal 180 (salmon-colored and purple-colored combo)
So, are vertical angles congruent? Yes! Vertical angles are congruent, meaning that they always have the same degree measure.
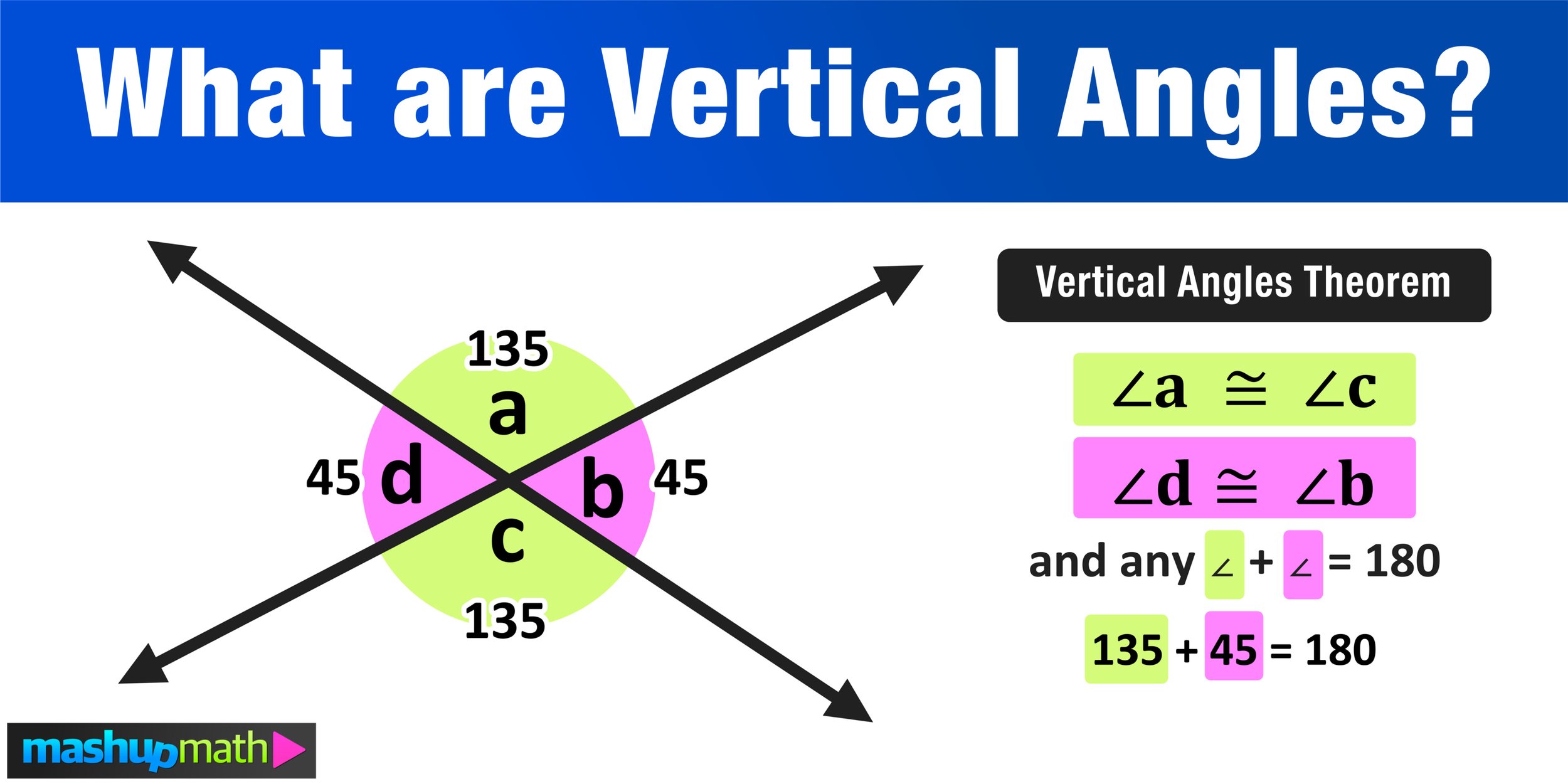
What is the Vertical Angles Theorem?
Now that you understand how to identify vertical angles and why vertical angles are always congruent, you are ready for the Vertical Angles Theorem.
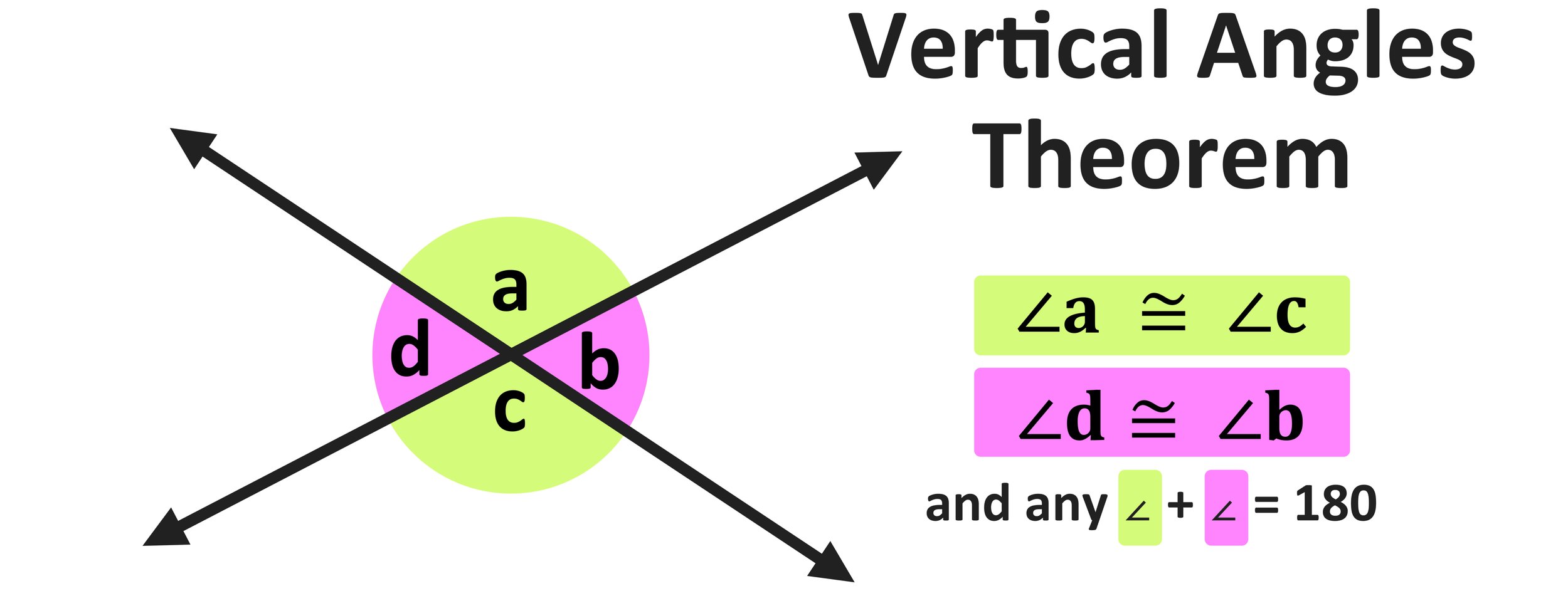
The Vertical Angles Theorem states that whenever two straight lines intersect, they form two sets of supplementary angles (linear pairs) that are congruent to each other. Namely, that the two pairs of vertical angles formed are congruent.
The theorem is shown in Figure 09 below:
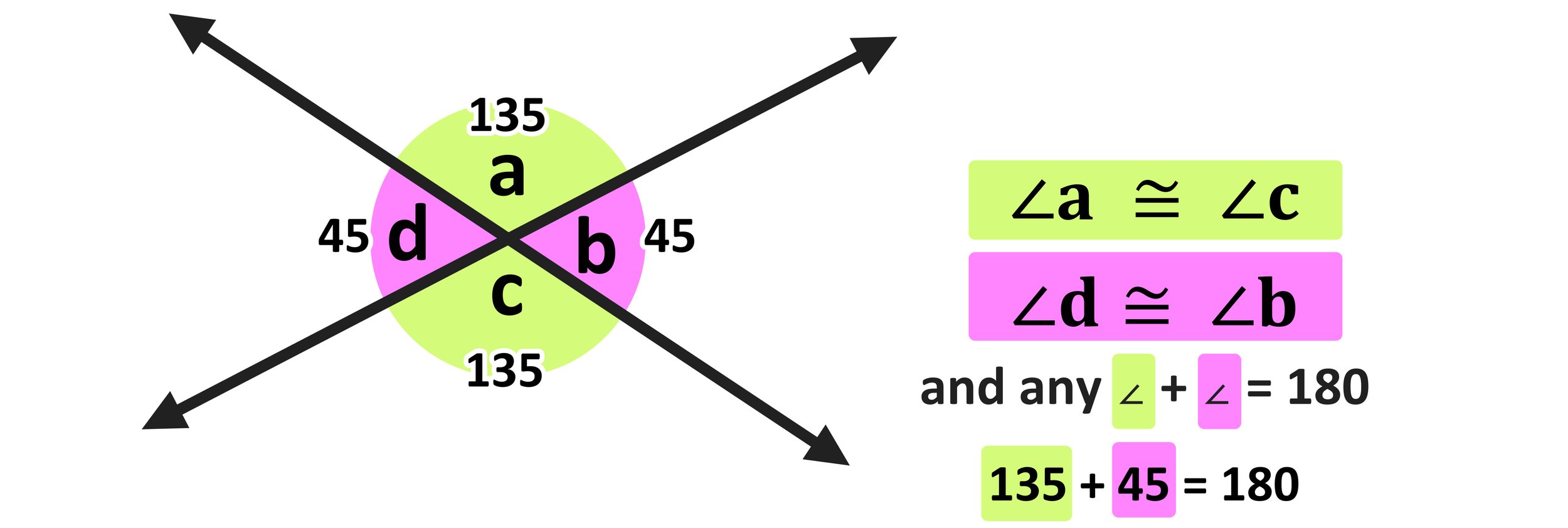
Figure 09: The Vertical Angles Theorem
Again, when two straight lines intersect, the vertical angles that are formed are always congruent (or equal) to each other. So, the green angles ∠a and ∠c are congruent, as well as the pink angles, ∠d and ∠b. Furthermore, any combination of a pink angle and a green angle will be a linear pair (supplementary) and they will have a sum of 180.
∠a ≅ ∠c
∠d ≅ ∠b
∠a + ∠b = 180, ∠b + ∠c = 180, ∠c + ∠d = 180, ∠d + ∠a = 180
So, if for example, you only that ∠a=135, you could use the Vertical Angles Theorem to figure out the angle measures of ∠b, ∠c, and ∠d.
Since ∠c is vertical to ∠a (and because vertical angles are congruent), ∠c also equals 135.
Furthermore, since ∠b is supplementary to ∠a, their sum must equal 180. 135 + ∠b = 180 means that ∠b=45.
And, Since ∠d is vertical to ∠b (and because vertical angles are congruent), ∠d also equals 45.
Therefore, as shown in Figure 10 below, you can use the Vertical Angles Theorem to find the value of all four angles formed by two intersecting lines when you only know the angle measure of one of them.
Figure 10: Color-coding is a helpful tool for visualizing the difference between vertical angles and linear pairs.
Now that you have a strong understanding of vertical angles and the vertical angle theorem, let’s take a look at 3 examples of vertical angles.
Example of a Vertical Angle #1
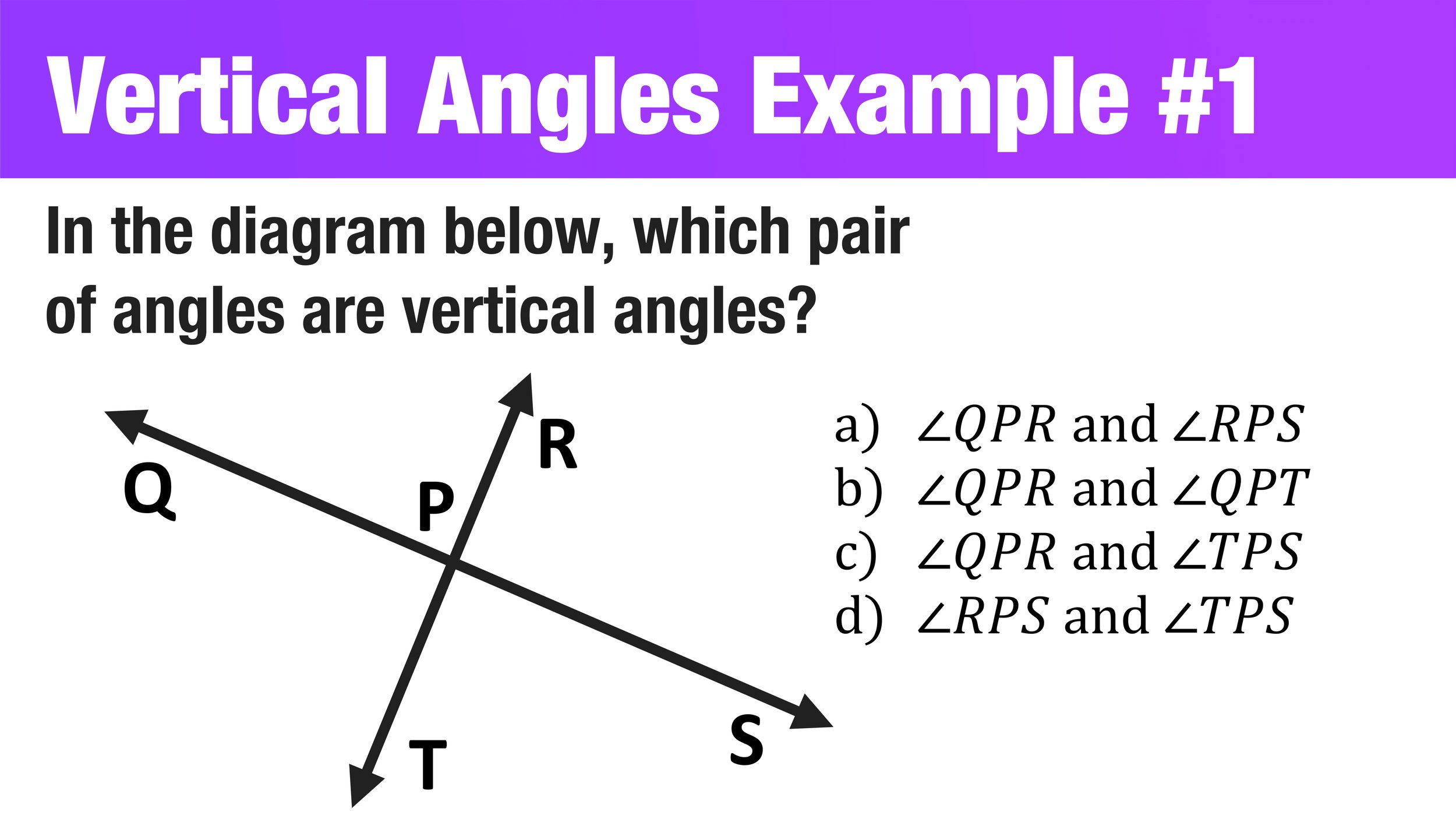
Take a look at the diagram below of two intersecting lines and identify which two angles is an example of a vertical angle pair.
Example of a Vertical Angle Pair #1 (original question)
To easily solve this problem, let’s color-code the diagram so that the vertical angles are the same color as follows:
Example of a Vertical Angle Pair #1 (after color-coding)
Now, it is easier to see that the green angles are vertical to each other and will have the same measure (they are congruent). The blue angles are also vertical to each other and congruent. And, any combination of a green angle and a blue angle is a linear pair with a sum of 180. We can make these conclusions by applying the Vertical Angles Theorem.
So, based on the four choices, we can conclude that choices A, B, and D are all linear pairs and that the only example of a vertical angle pair is choice B.
Example of a Vertical Angle Pair #1: Choice C is the answer
Example of a Vertical Angle #2
Let’s take a look at another example similar to the previous one.
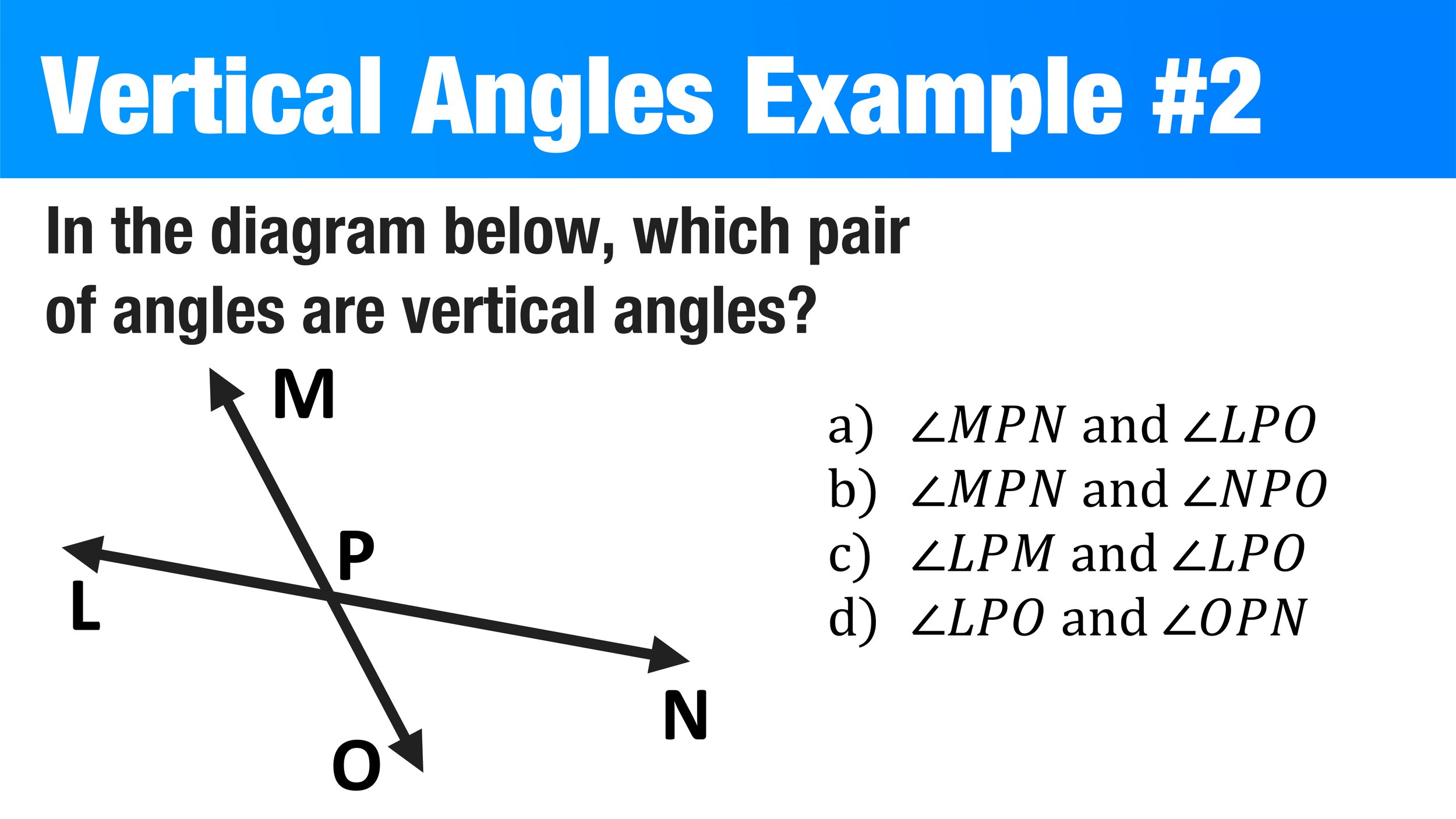
Example of a Vertical Angle Pair #2: (original question)
Just like the first example, start by color-coding the diagram to clearly identify the vertical angle pairs and the linear pairs:
Example of a Vertical Angle Pair #2: (after color-coding)
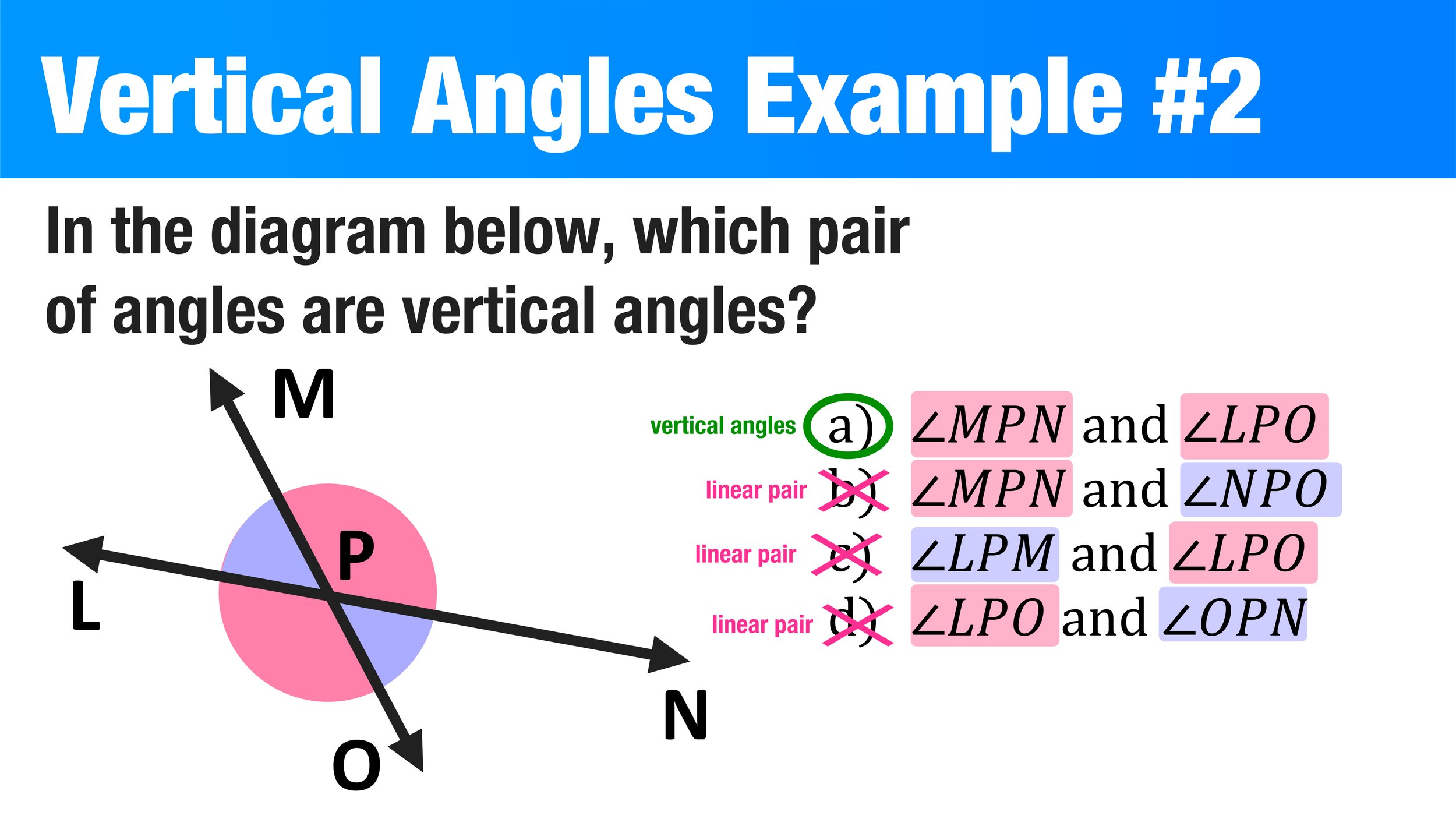
Now, you can see that the pink angles are vertical and congruent to each other and that the purple angles are also vertical and congruent to each other. Also, the Vertical Angles Theorem allows you to conclude that any combination of a purple angle and a pink angle will be a linear pair with a sum of 180.
Looking at all four choices, you can conclude that choices B, C, and D are all linear pairs and that the only example of a vertical angle pair is choice A.
Example of a Vertical Angle Pair #2: Choice B is the answer
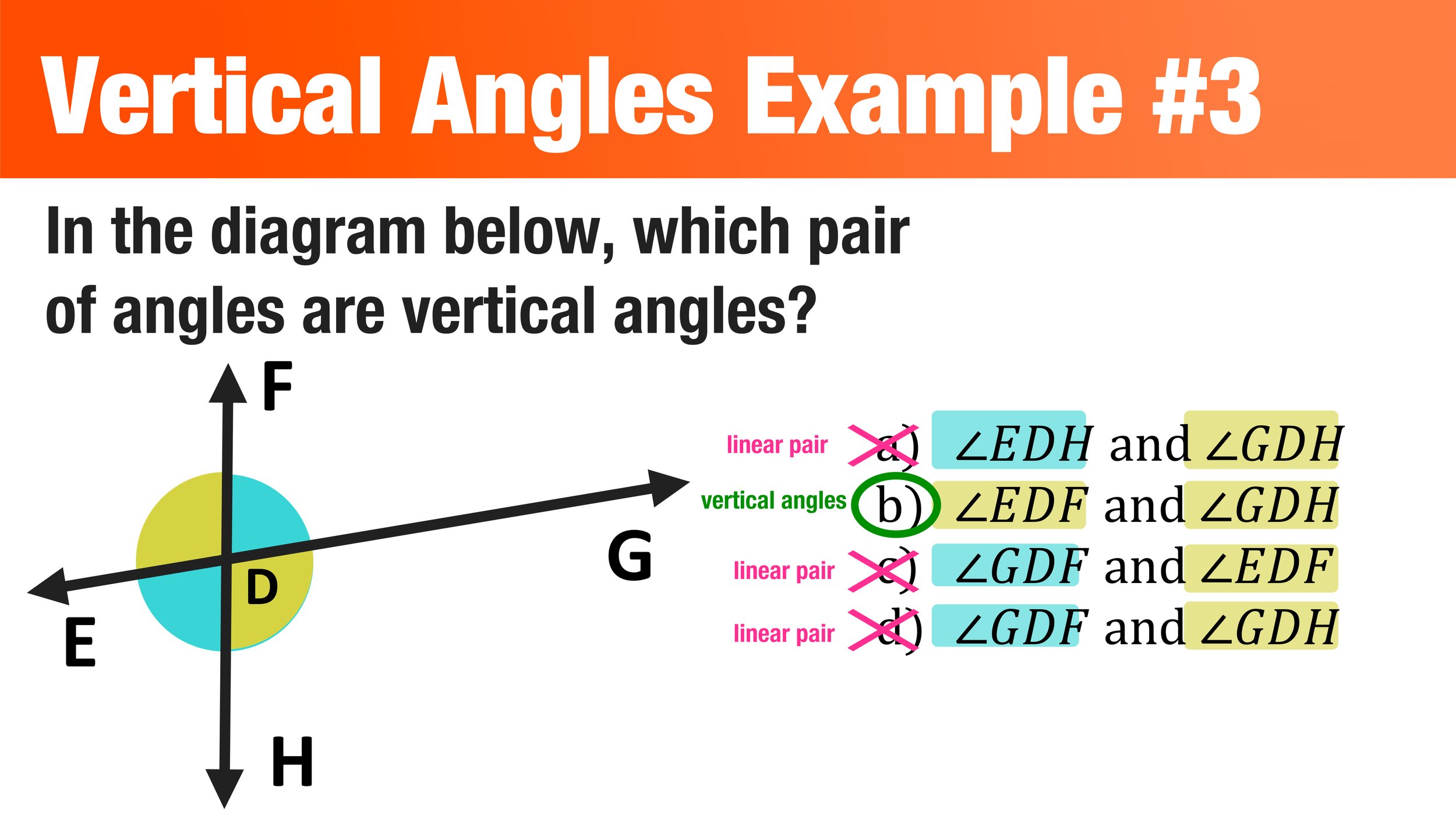
Example of a Vertical Angle #3
Finally, here is one last example where you have to identify a vertical angle by looking at a given diagram.
Example of a Vertical Angle Pair #3: (original question)
Continue by color-coding the diagram as follows:
Example of a Vertical Angle Pair #3: (after color-coding)
After color-coding, you can see that the gold angles are vertical and congruent to each other and that the teal angles are also vertical and congruent to each other. Plus, according to the Vertical Angles Theorem, any combination of a gold angle and a teal angle will have a sum of 180 (since they are linear pairs and not vertical to each other).
To solve the problem, you can look at all four choices and conclude that A, C, and D are all linear pairs and that the only example of a vertical angle pair is choice B.
Example of a Vertical Angle Pair #3: Choice B is the answer