What is 0.75 as a fraction?

In math, it is important to be able to convert values from decimal form to fraction form. Whether you make these conversions by making mental computations or by referencing guides like this very page, the most important thing is to understand the key concept that decimals and their corresponding equivalent fractions are equal to same value, thus making them interchangeable. In the case of .75 as a fraction, knowing the answer by heart is incredibly useful given that this value comes up extremely often in math problems. Below, you will learn what is 0.75 as fraction and how you can make this conversion on your own by following a few simple steps.

Answer: 0.75 as a fraction equals 3/4

Now that you know that .75 as a fraction is equal to 3/4 (i.e. three-fourths or three-quarters), let’s learn the math behind this conversion":

Why is .75 as a fraction 1/4?

To convert 0.75 as a fraction (or any other decimal), we will be using the following 3-step process:

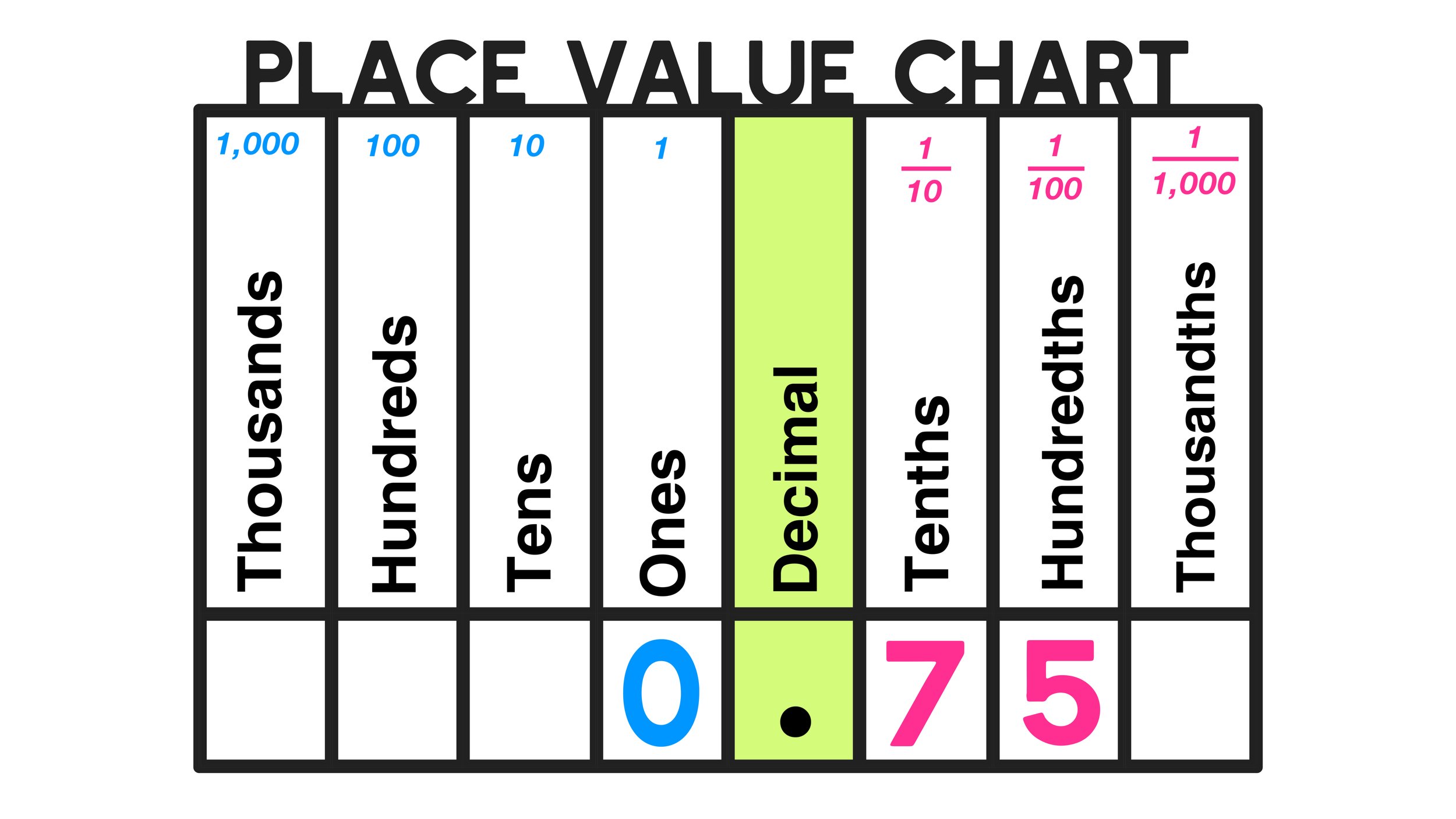
Step #1: To convert any decimal to a fraction (we will be working with 0.75 in this example), the first step is to identify the place value of the very last digit (i.e. the digit that is most far to the right of the decimal point). The very last digit of 0.75 is 5, which sits in the hundredths place value slot.

If figuring out a digit’s place value slot is confusing, we recommend using a place value chart as a visual aide as shown below in Figure 01:

Ready to learn how to convert any number in decimal form into a fraction? Click here to access our free student guide: How to Convert a Decimal to a Fraction in 3 Easy Steps

Step #2: The next step is to take whatever decimal you are working with and rewrite it as a fraction over the number one as follows:

0.75/1

Once you have rewritten .75 as a fraction with a denominator of 1, continue on by multiplying both the top and bottom of the fraction by the place value that you identified in Step #1, which was 100 since the final digit was in the hundredths place value slot.

(0.75 x 100) / (1 x 100) = 75/100

Notice that the result, 75/100, is a fraction that is equivalent to 0.75, but it is not the fraction 1/4 that we saw earlier. Why is it different? Because the fraction 75/100 can be simplified…

Step #3:

For this final step, we want to see if we can simplify the result from Step #2, which was 75/100. To do this, we have to see if there exists a Greatest Common Factor (GCF) between the numerator and denominator. If a GCF exists, you can simply divide the top and bottom of the fraction by this value to find an equivalent fraction that is in simplest form.

How do we check for a GCF? Start by listing all of the factors of both the numerator (75) and the denominator (100), as shown below:

With this in mind, let’s go ahead and list the factors of 25 and 100 below:

• Factors of 75: 1, 3, 5, 15, 25, 75

• Factors of 100: 1, 2, 4, 5, 10, 20, 25, 50, 100

By listing out all of the factors, it’s easy to see that the Greatest Common Factor of both values is 25.

Since we have found a GCF, we know that the fraction can be simplified by dividing it into the numerator (75) and the denominator (100) as shown below:

(75 ÷ 25) / (100 ÷ 25) = 3/4

Conclusion: .75 as a fraction is 3/4

Keep Learning:

Tags: what is .375 as a fraction, what is 0.375 as a fraction, what is 375 as a fraction, what's 375 as a fraction, .375 as a fraction, 0.375 as a fraction, .375 as fraction, 375 as a fraction, what is .375 as a fraction, 375 as a fraction in simplest form,