What is a Composite Number?

Everything You Need to Know About Composite Numbers in Math

In math, there are two different ways to categorize and classify numbers based on how many factors they have.

When a whole number has only two factors—namely itself and 1—then it is considered to be a prime number. However, when a whole number has three or more factors, it is considered a composite number, meaning that it has more than two factors and it is not prime. Since most numbers have more than two factors, we can say that most numbers are indeed composite numbers.

This free guide to composite numbers will further explore the difference between a composite number and a prime number and how to determine whether any given number is composite or prime. The guide is made up of the following sections and you can use the quick-links below to jump to any particular section (or you can follow each section in order):

What is a Prime Number? What is a Composite Number?
How to Determine if a Number is Composite or Prime
Composite Number Examples
Is 1 a Composite Number?
Interesting Facts and Properties of Composite Numbers
Conclusion: Composite Numbers

What is a Prime Number? What is a Composite Number?

Prime Numbers

Generally speaking, whole numbers fall into two categories: Prime Numbers and Composite Numbers.

Definition: A whole number is considered a prime number if it can only be divided by itself and 1. In other words, prime numbers have only two factors.

Note that 0 and 1 are not prime because they only have one divisor each.

However, numbers such as 2, 3, and 5 are considered prime numbers because they are only divisible by 1 and themselves:

Factors of 2: 1, 2
Factors of 3: 1, 3,
Factors of 5: 1, 5

Composite Numbers

Definition: A whole number is considered a composite number if it has more than two factors, meaning that the number is divisible by a number other than 1 and itself.

For example, the numbers 4 and 6 are composite numbers (not prime numbers) because each number has more than two divisors:

Factors of 4: 1, 2, and 4 (4 has three divisors)
Factors of 8: 1, 2, 4, and 8 (8 has four divisors)

It is important for students to understand the difference between a prime number and a composite number because every whole number (other than 0 and 1) is either prime or composite.

The chart in Figure 03 below shows the distribution of prime numbers and composite numbers from 1-100.

Here is a list of all of the composite numbers up to 100:

4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81,82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, and 100

And here is a list of all of the prime numbers up to 100:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97

Again, notice that 0 and 1 are not included on either of these lists because 0 and 1 are neither composite nor prime.

Note that the key difference between a prime number and a composite number is that a composite number has more than two factors and a prime number has exactly two factors (one and itself). Composite numbers are much more common than prime numbers and the only whole numbers that are not considered composite or prime are 0 and 1.

Now that you understand the difference between a prime number and a composite number, let’s a deeper dive into composite numbers and their unique characteristics.

What is a Composite Number in Math?

If you need to determine or prove that a number is prime or composite, you simply have to find all of the factors of that number. If the number has only two factors (1 and itself), then it is prime. On the other hand, if the number has three or more factors, then it is considered composite.

Let’s consider a few examples of determining whether or not a given number is a composite number:

Example #1: Is 18 a composite number?

Let’s start by finding all of the factors of 18 as follows:

18 ÷ 1 = 18
18 ÷ 2 = 9
18 ÷ 3 = 6
18 ÷ 6 = 3
18 ÷ 9 = 2
18 ÷ 18 = 1

So, the factors of 18 are 1, 2, 3, 6, 9, and 18.

Clearly, 18 has more than two factors, so we can say that:

Final Answer: 18 is a composite number.

Example #2: Is 37 a composite number?

After some trial-and-error, you will see that 37 is only divisible by 1 and itself.

So, the factors of 36 are 1 and 36.

In cases like this, when a number can only be factored by 1 and itself, we know that the number is prime (not composite).

Final Answer: 37 is a prime number (i.e. it is not a composite number)

Example #3: Is 51 a composite number?

Let’s go ahead and use the same procedure from the previous two examples to determine whether or not 51 is a composite number.

At first glance, you may think that 51 is a prime number, but it actually has more than two factors:

51 ÷ 1 = 51
51 ÷ 3 = 17
51 ÷ 17 = 3
51 ÷ 51 = 1

Because 51 can be divided by 3, we know that it is a composite number with the following factors: 1, 3, 17, and 51

Final Answer: 51 is a composite number.

Example #4: Is 79 a composite number?

After attempting to evenly divide numbers into 79, you will see that 79 has only two factors: 1 and itself.

So, by definition, we know that 79 is a prime number and that the factors of 79 are 1 and 79.

Since we know that 79 is prime and not composite, we can conclude that:

Final Answer: 79 is a prime number.

Example #5: Is 1 a composite number?

For this final example, let’s determine whether 1 is a composite number, a prime number, or neither.

Remember that prime numbers have exactly two factors and composite numbers have three or more factors.

But how many factors does one (1) actually have? The only number that divides evenly into 1 is itself (1), so 1 has only one factor.

The fact that 1 has only 1 factor means that it does not meet the criteria to be a prime number and it also does not meet the criteria to be a composite number, so we must conclude that 1 is neither composite nor prime.

Final Answer: 1 is neither a composite number nor a prime number (i.e. it is neither).

As long as you can list the factors of a given number, you can determine if it is a prime number or a composite number based on the following criteria:

Exactly 2 Factors (1 and itself): The number is prime.
More than 2 Factors (3 or more): The number is composite.

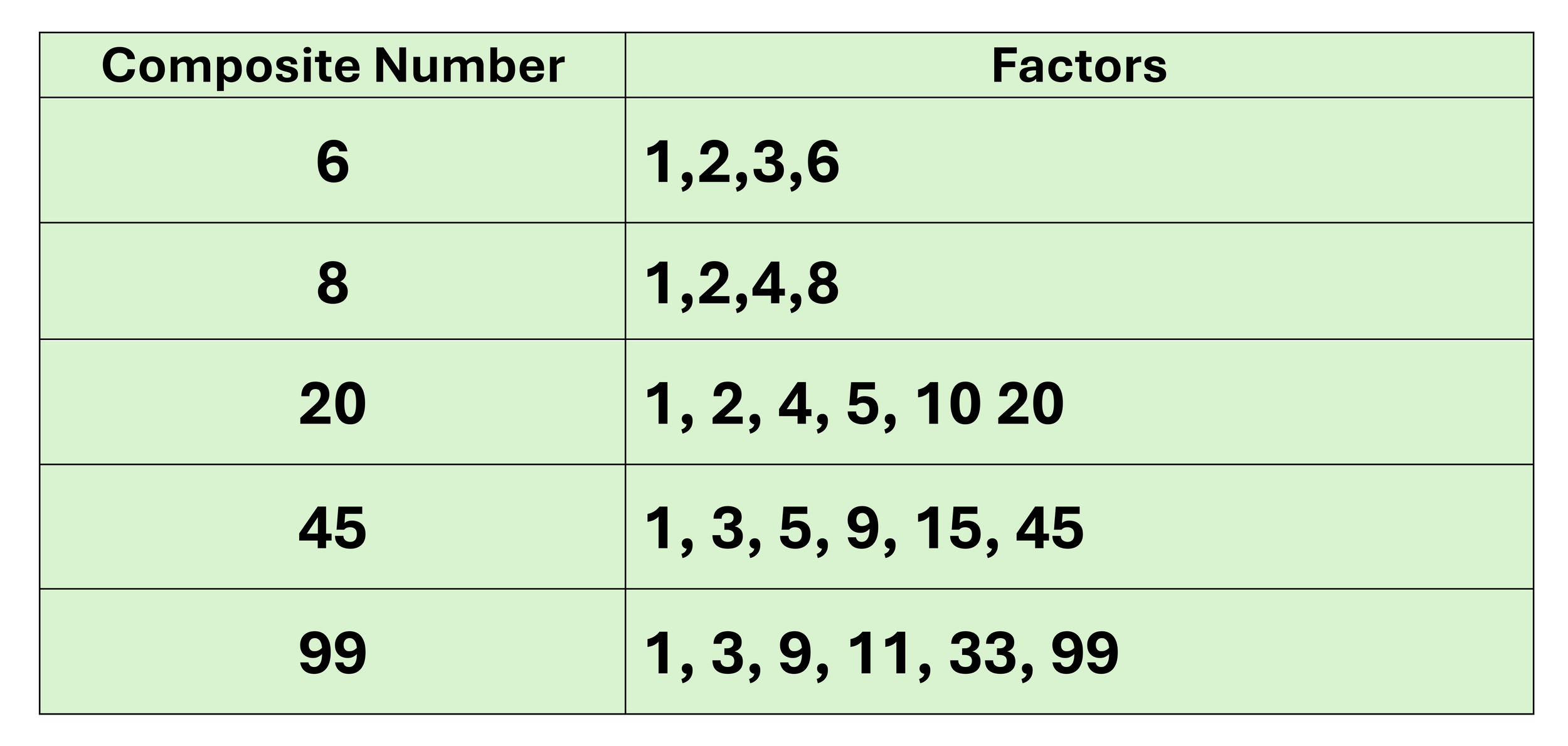
The table in FIGURE X below shows a few more examples of composite numbers and their factors.

All of the examples of composite numbers in the table above have three or more factors, which means that they are, by definition, not prime (i.e. they are all composite numbers).

Is 1 a Composite Number?

At this point, you may be wondering “is 1 a composite number”? In the case of the number 1, we can easily list all of its factors as follows:

Factors of 1: 1

Clearly, the only factor of 1 is 1. For a number to be composite, it must have more than two factors, which 1 obviously does not, so 1 is not a composite number.

Conclusion: Is 1 a Composite Number? No, because it does not have more than two factors.

Is 1 a Prime Number?

Now that we know that 1 is not a composite number, we can explore the question “is 1 a prime number?”.

Remember that, by definition, a number is prime if it has only two factors (1 and itself). Since the number 1 has only factor, it does not meet the criteria for it to be a prime number either.

Conclusion: Is 1 a Prime Number? No, because it does not have exactly two factors.

Composite Numbers: Interesting Facts and Properties

Here are some more interesting facts about composite numbers and prime numbers:

0 and 1 are the only whole numbers that are neither composite nor prime.
Every even number other than 2 is a composite number (the number 2 is prime).
Every composite number has at least three factors.
2 is the smallest prime number.
4 is the smallest composite number.
The smallest composite number is 4
There are two types of composite numbers: even composite numbers and odd composite numbers

The Two Types of Composite Numbers

Thee last interest property about composite numbers listed above stated that there are two types of composite numbers: even and odd.

Even Composite Numbers are easy to identify because every even number other than 2 is a composite number. For example, 4, 6, 8, 10, 20, 44, and 92 are all even composite numbers. All of these numbers are divisible by 1, itself, and 2. Since all of these numbers have more than two factors, they meet the criteria for composite numbers.

Odd Composite Numbers are a bit more difficult to identify than even composite numbers. It is a fact that every odd whole number that is not a prime number is a composite number (not including 1). For example, 7, 9, 13, 25, 51, and 99 are all odd composite numbers. All of these numbers have three or more factors and are not divisible by two nor are they prime.

What is a Composite Number?: Conclusion

In math, almost every whole number can be categorized as either a composite number or as a prime number. If a whole number has exactly two factors (1 and itself), then it is called a prime number. For example, 3, 11, and 59 are all prime numbers because they each have exactly two factors. If a whole number has more than two factors, then it is called a composite number. For example, 8, 20, and 78 are all composite numbers because they each have three or more factors. Every even whole number greater than 2 is a composite number. Every odd whole number greater than 1 that isn’t prime is also a composite number. Composite numbers are much more common than prime numbers. The numbers 0 and 1 are the only whole numbers that are neither prime nor composite because they both have exactly 1 factor (meaning that 0 and 1 fail to meet the criteria to be prime or composite).

You can determine whether a given number is a prime number or a composite number by listing all of its factors and then counting them. If the number has exactly two factors (1 and itself), then it is prime. If the number has three or more factors, then it is composite.

For example:

19 → Factors: 1, 19 → Exactly Two Factors → Prime Number
27 → Factors: 1, 3, 9, 27 → More Than Two Factors → Composite Number

As long as you can remember this key difference between a prime number and a composite number, you can easily determine whether or not any given number is prime or composite.