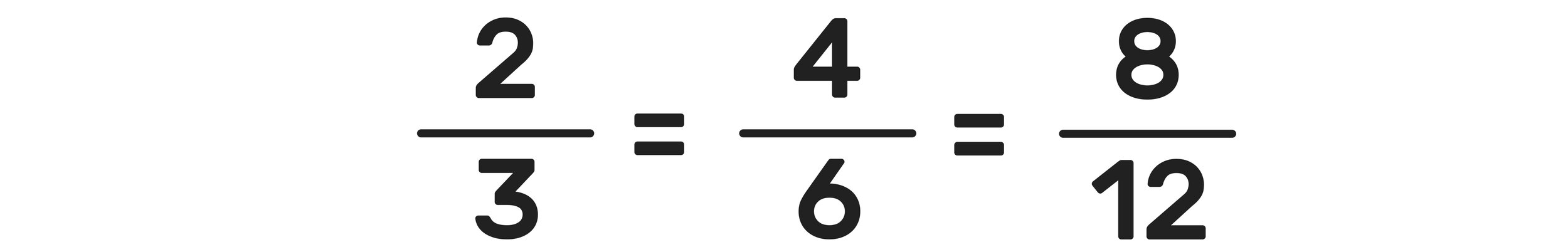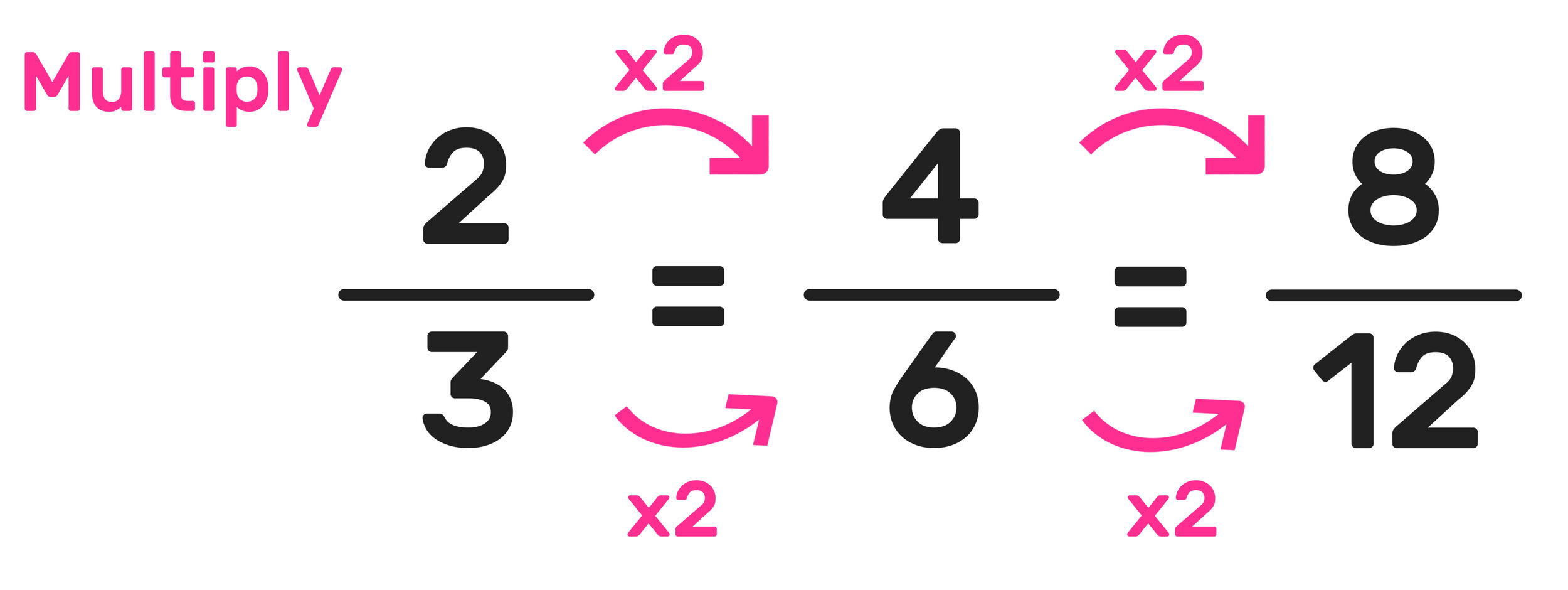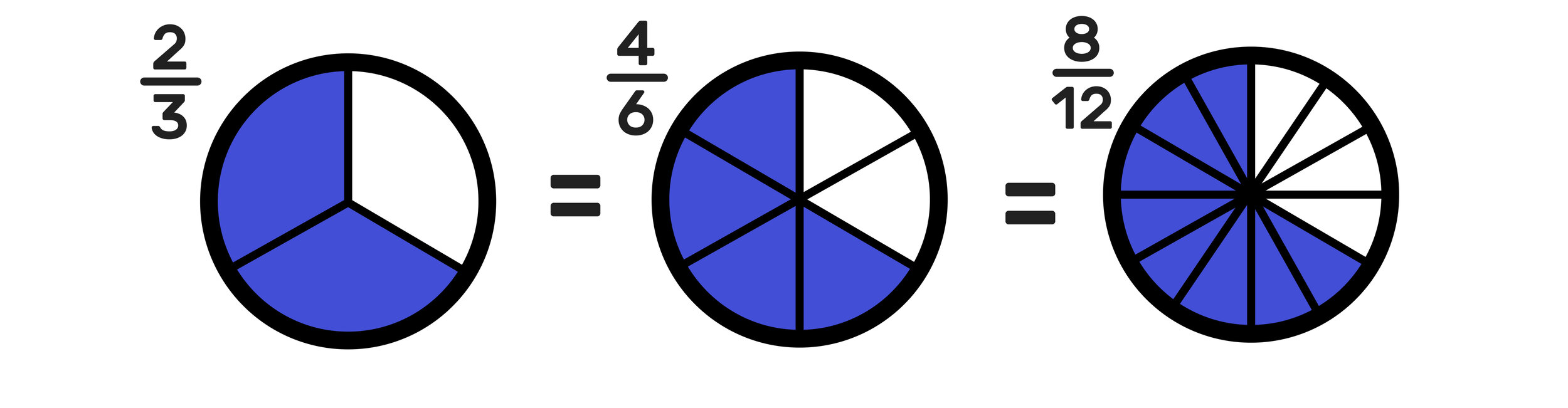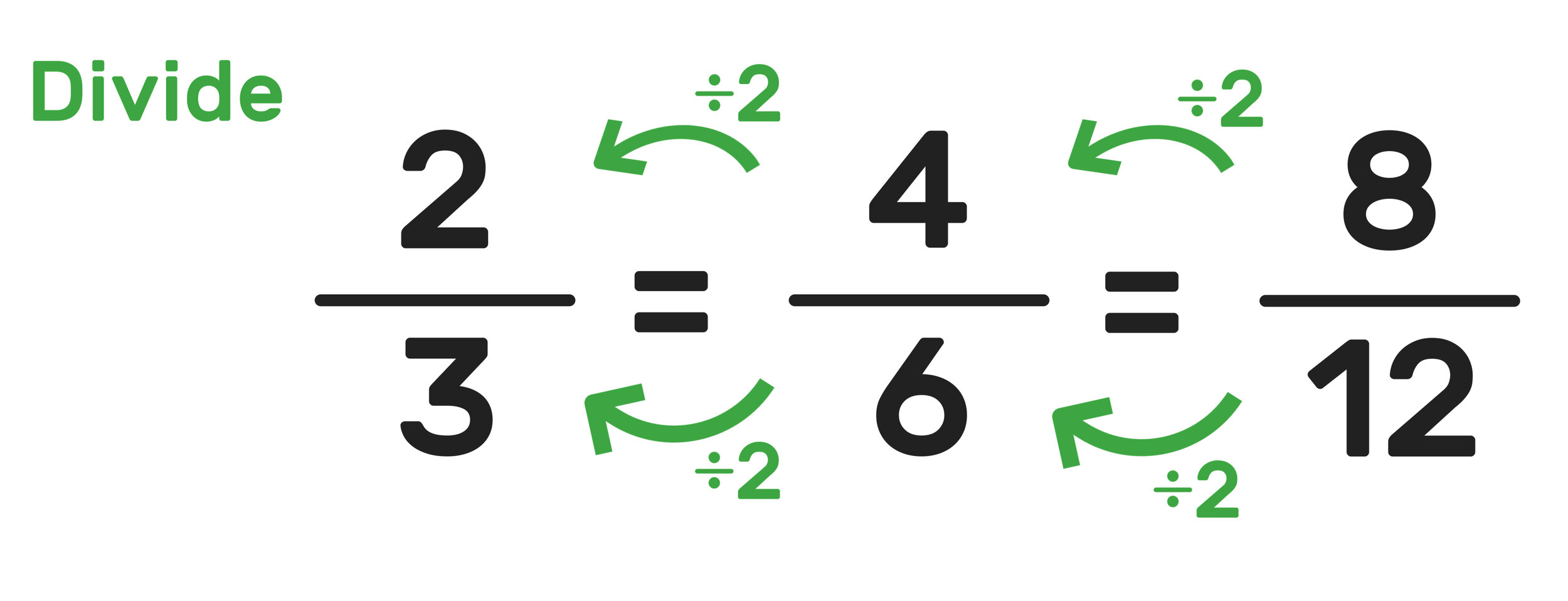Equivalent Fractions Explained!
What are equivalent fractions in math?
Image Source: Mashup Math FP
Fractions are one of the most important foundational topics in math and students need to understand how to perform operations on fractions like adding and subtracting fractions and multiplying fractions. But, before students can understand fractions at an advanced level, it is critical that they have a strong grasp of equivalent fractions.
In real life, we often deal different values that can be considered equivalent or equal to each other. For example, we know that 60 minutes is equivalent to 1 hour and we also know that 16 ounces are equivalent to one pound. In each case, we are expressing the same amount of time or weight in two different ways that are interchangeable.
This idea of expressing two equal values in different ways is similar in math when it comes to equivalent fractions.
This complete guide to equivalent fractions will provide a step-by-step tutorial on how to understand equivalent fractions and how to find them.
First, let’s start with the equivalent fractions definition:
Math Definition: Equivalent Fractions
Equivalent fractions are fractions that have the same value but do not look the same.
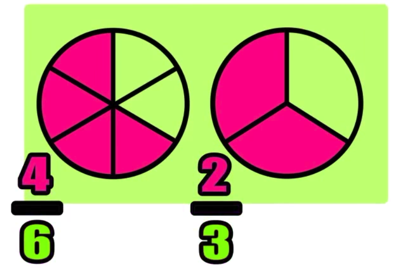
For example, 4/6 and 2/3 are equivalent fractions because they both represent “two thirds.”
Let’s take a look at this example a little closer:
Why are 2/3 and 4/6 equivalent fractions?
Notice that there are three different fractions above: 2/3, 4/6, and 8/12
All three fractions are equivalent fractions. But why?
The reason why they are equivalent fractions is because when you either (A) MULTIPLY or (B) divide both the numerator (top) and denominator (bottom) of each fraction by the same number, the fraction doesn’t change. (If this idea is hard to understand, the images below will help!).
Visual Representation:
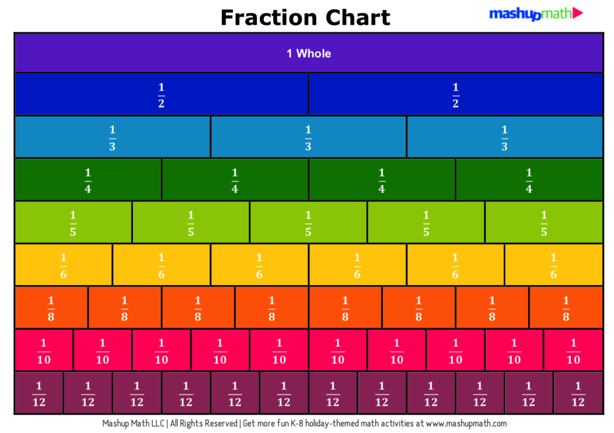
You can also use a fraction chart as a visual aid to help you to understand and identify equivalent fractions.
What about Dividing?
To find equivalent fractions by dividing, take the same steps as multiplying, but mind the following key points:
Divide both the numerator (top) and denominator (bottom) of each fraction by the same number
Make sure that whatever number you choose to divide by results in only whole numbers (no decimals)
Continue dividing until you can not go any further without getting a decimal. At this point, you will have reduced the fraction as much as possible.
Again, you can see that 2/4, 4/6. and 8/12 are equivalent fractions.
How to Test if Two Fractions are Equivalent Using Cross Products:
If you are unsure of whether or not two fractions are equivalent, there is an easy shortcut involving multiplication that you can use as a test.
Rule: Two fractions are equivalent if their cross products are equal.
To find the cross products of two fractions, multiply the top of the first fraction by the bottom of the second fraction AND the bottom of the first fraction by the top of the second fraction.
Equivalent Fractions Example 01: 4/5 and 12/15
To see whether or not 4/5 and 12/15 are equivalent to each other, you have to start by finding the cross products.
Again, multiply the top of the first fraction by the bottom of the second fraction AND the bottom of the first fraction by the top of the second fraction as follows:
4 x 15 = 60
5 x 12 = 60
Notice that both of the cross products equals 60.
Therefore, we can conclude that 4/5 and 12/15 are equivalent fractions because their cross products are the same.
Equivalent Fractions Example 02: 4/7 and 6/12
Just like the last example, you can test to see if the two fractions are equivalent by finding the cross products as follows:
4 x 12 = 48
7 x 6 = 42
Notice that the cross products are not equal: 48 ≠ 42
Therefore, we can conclude that 4/7 and 6/12 are NOT equivalent fractions because their cross products are NOT the same.
Conclusion:
Equivalent fractions are fractions that have the same value but do not look the same or have the same numbers.
You can create or test equivalent fractions by either multiplying or dividing both the numerator or the denominator by the same number.
When dividing, you can only work with results that are whole numbers (no decimals!).
To test whether or not two fractions are equivalent, find the cross products. If the cross products are equal, then the fractions are equivalent.
Need Extra Practice?
Free Worksheet:
⤓ Download Your Free Equivalent Fractions Practice Worksheet and Answer Key
Exploring Equivalent Fractions: Video Tutorials
Still confused? Check out the animated video lessons below:
Check out the video lesson below to learn more about equivalent fractions and ratios and for more free practice problems:
More Free Fractions Lessons:
Have thoughts? Share your thoughts in the comments section below!
(Never miss a Mashup Math blog--click here to get our weekly newsletter!)
By Anthony Persico
Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.