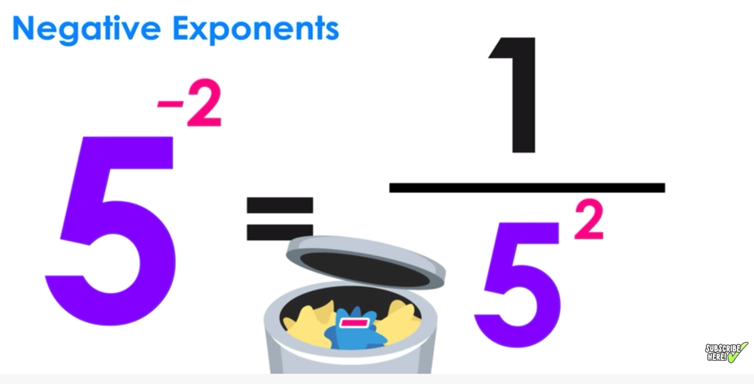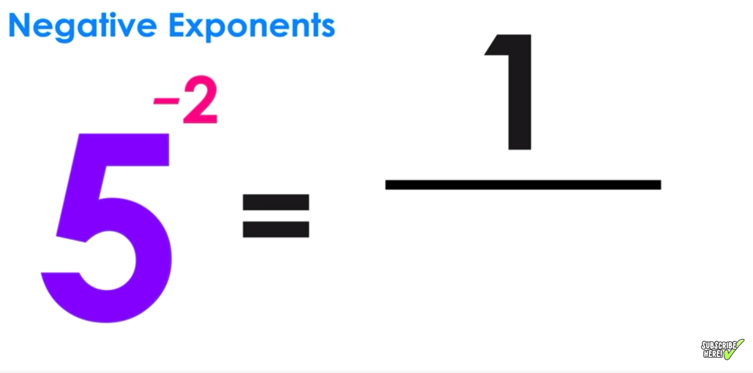Understanding the Negative Exponent Rule
Before you learn to understand and apply the Negative Exponent Rule, let’s recap what you already know about positive exponents.
For example, 5^2, or 5 squared, is equal to 5x5, or 25.
But what would change if the exponent (2 in this case) was negative instead of positive?
In math, when you think of the word negative or negate, the implication is that you must perform the opposite or inverse operation.
With positive exponents, you perform multiplication.
So, with negative exponents, you perform the opposite or inverse of multiplication, which is…
Division (because division is the inverse operation of multiplication).
Now you are ready to use the Negative Exponent Rule
Negative Exponent Rule in 3 Easy Steps
Now let’s look at the previous example again, except this time the exponent is -2 (negative two).
Step One: Rewrite the Value with Negative Exponent as a Fraction
Since we are performing division (the inverse of multiplication), we will rewrite the value as a fraction with a numerator of one.
Step Two: Trash the Negative Sign and Move the Value to the Denominator
To complete the fraction, get rid of the negative sign in front of the exponent and move the remaining value (5 squared) to the denominator of the fraction.
Notice that 5 to the negative second power is equal to one over 5 to the positive second power.
Step Three: Trash the Negative Sign and Move the Value to the Denominator
The final step is to simplify rewriting 5 squared as 25 and concluding that 5^-2 is equal to 1/25 or 0.04.
Expressed as a fraction.
Expressed as a decimal.
Looking for a visual representation of how the negative exponent rule works?
Check out the free video lesson below to learn more about how the negative exponent rule.
Free Negative Exponents Worksheet
This lesson includes a free Negative Exponent Rule worksheet that accompanies the video lesson. Click the link below to get yours!
Download your free Negative Exponents Worksheet Lesson Guide PDF
Share your ideas, questions, and comments below!
(Never miss a Mashup Math blog--click here to get our weekly newsletter!)
By Anthony Persico
Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.