Here's an Awesome Way to Teach Kids Fractions

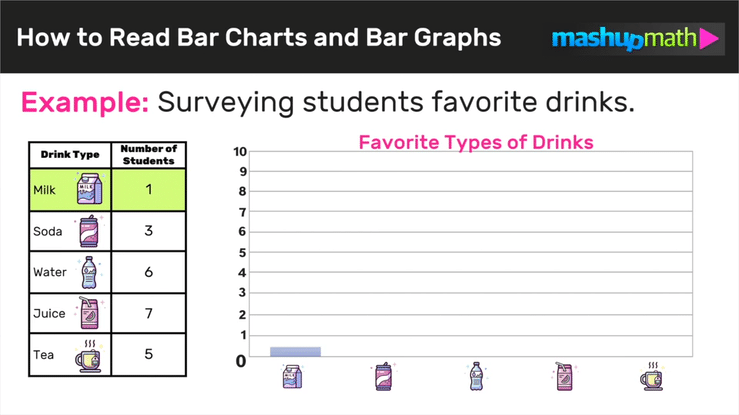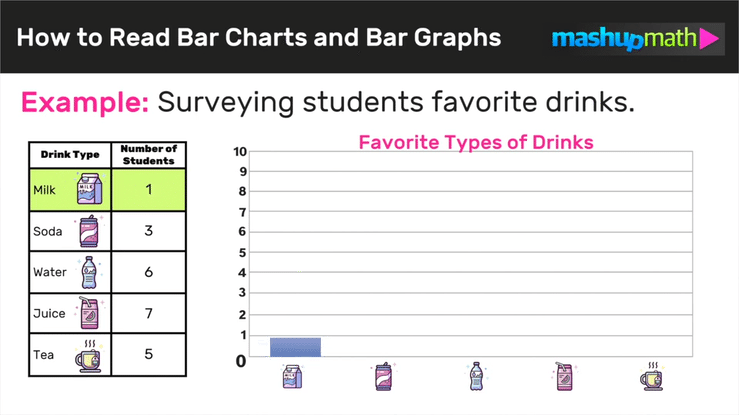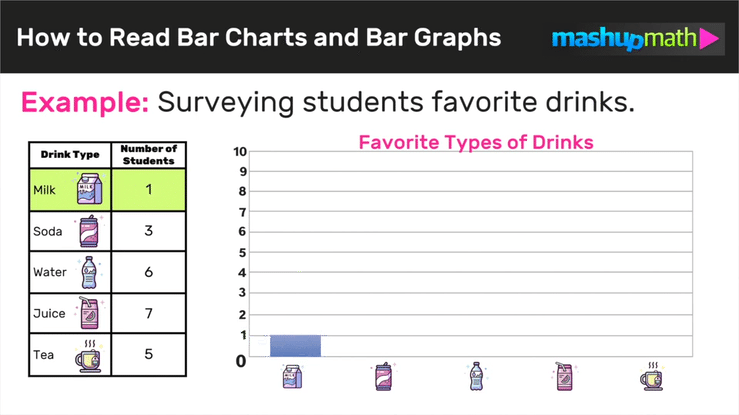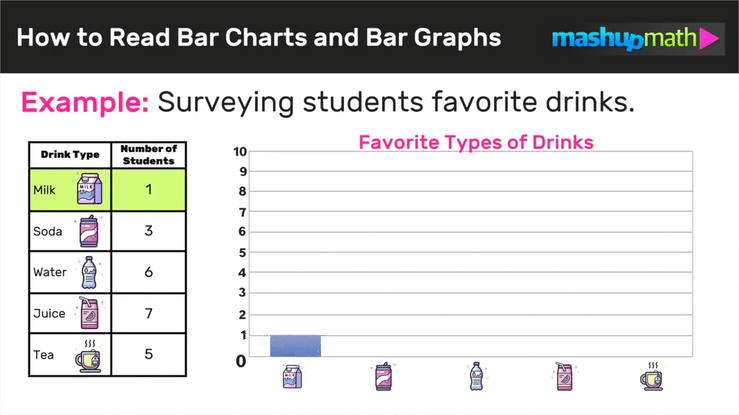
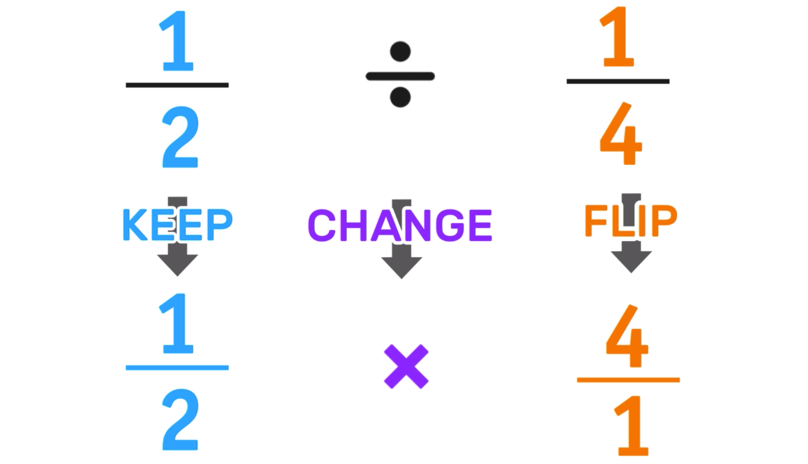
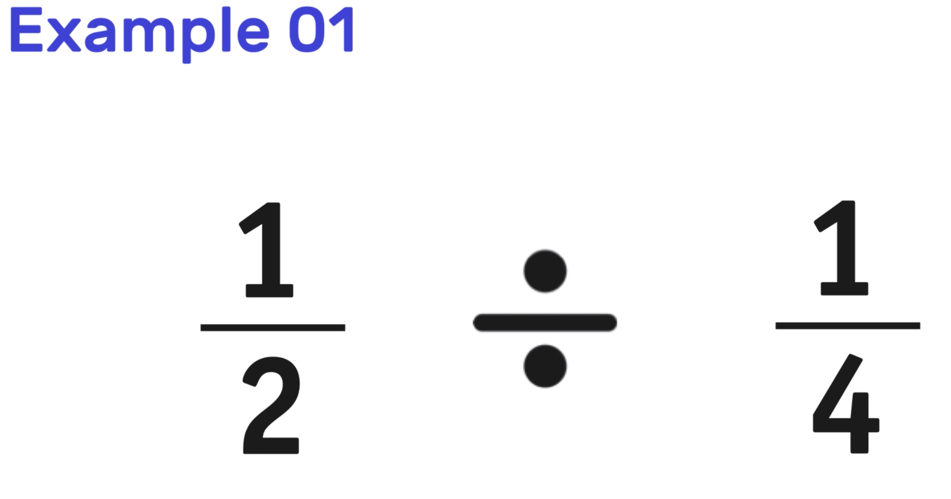
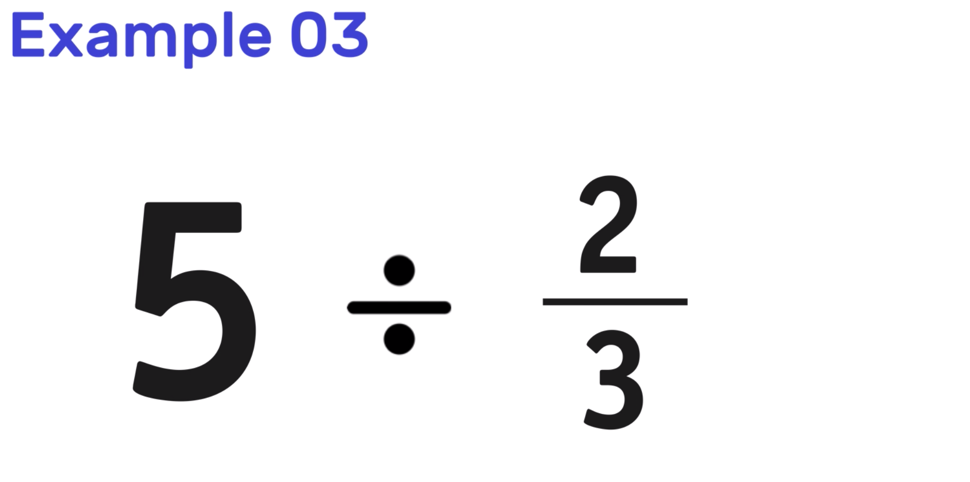
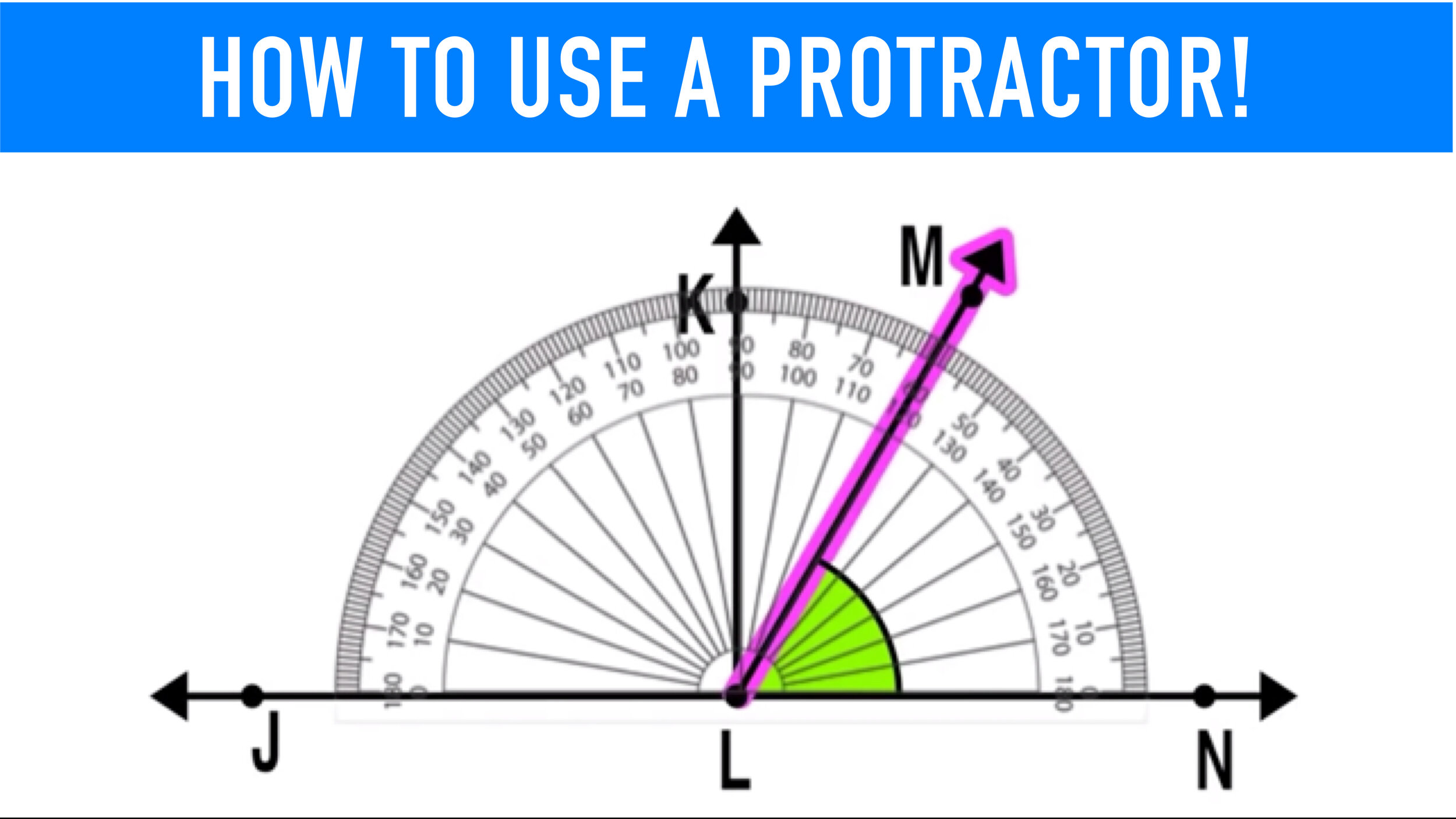
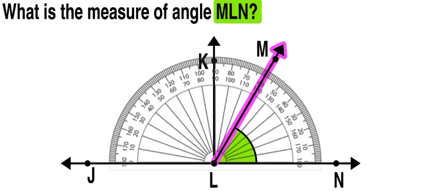
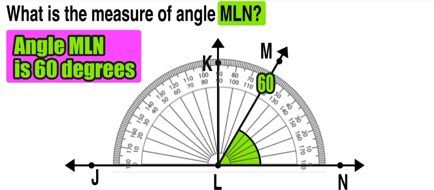
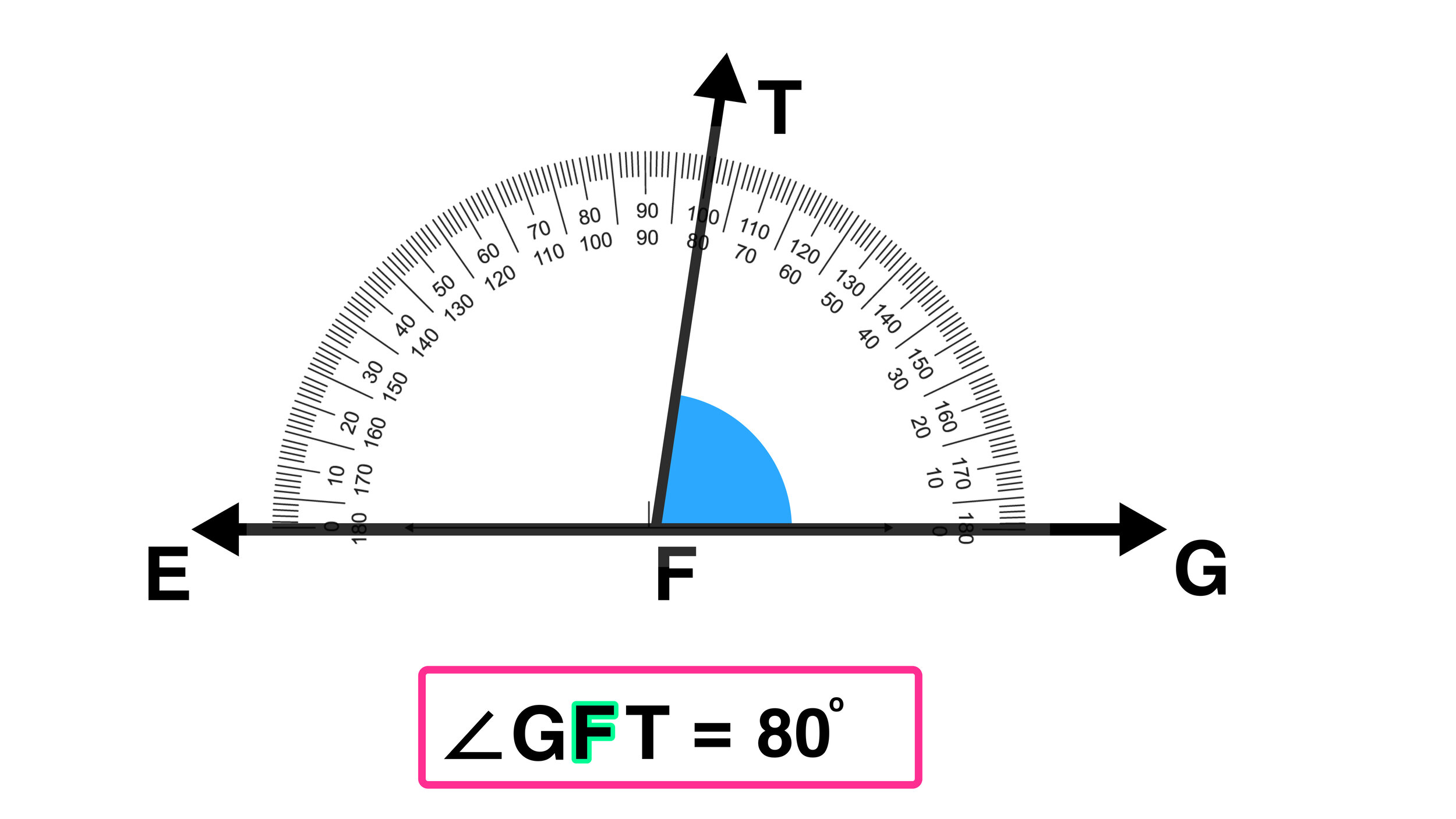
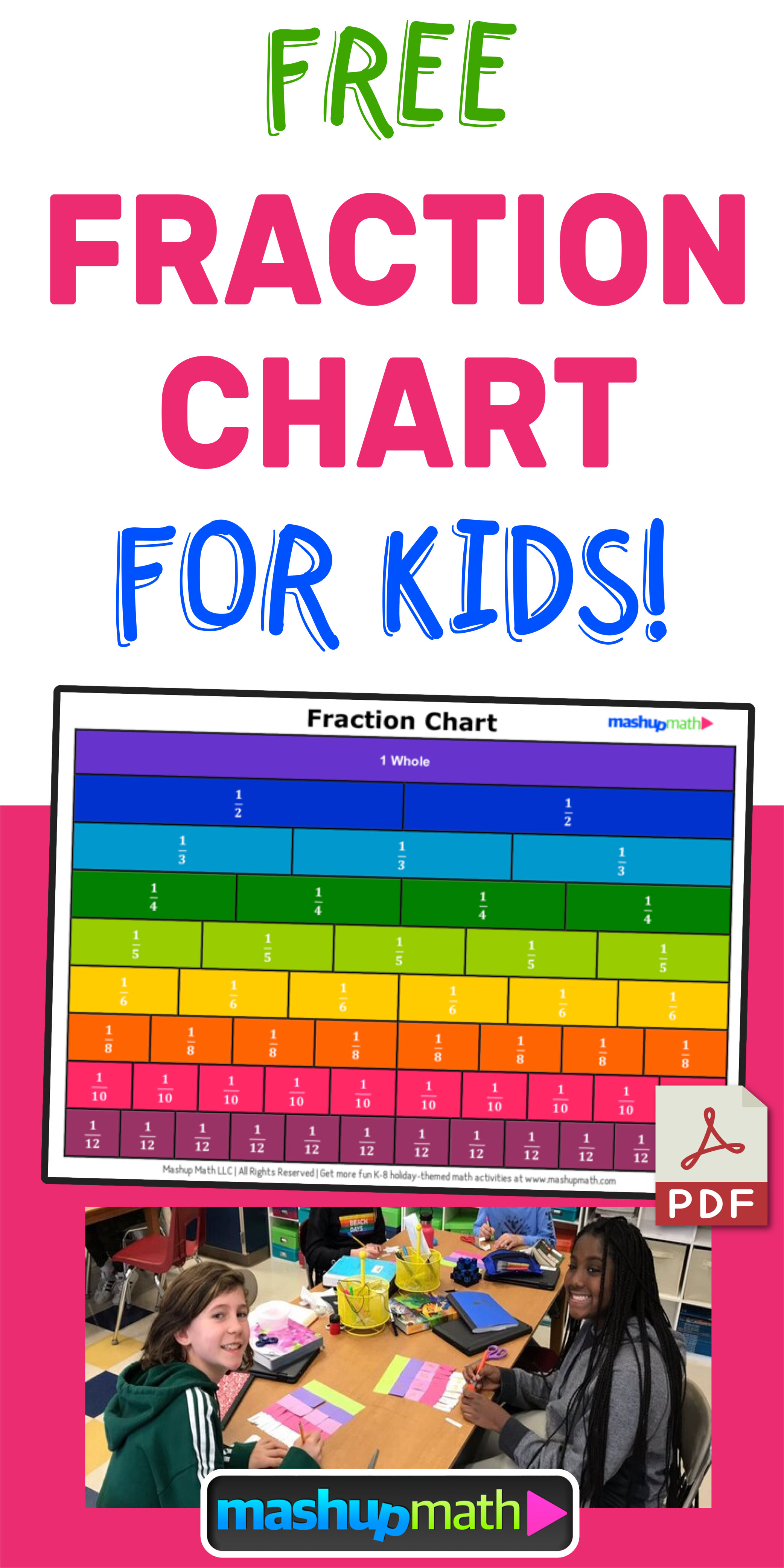
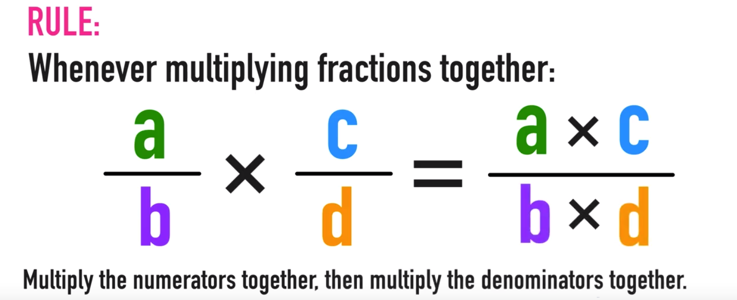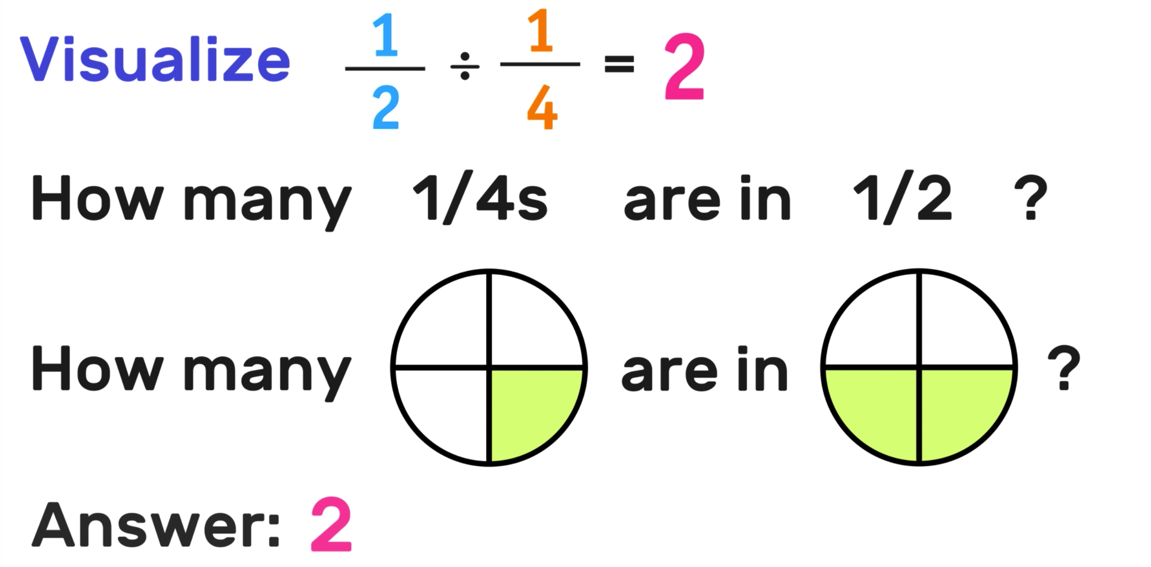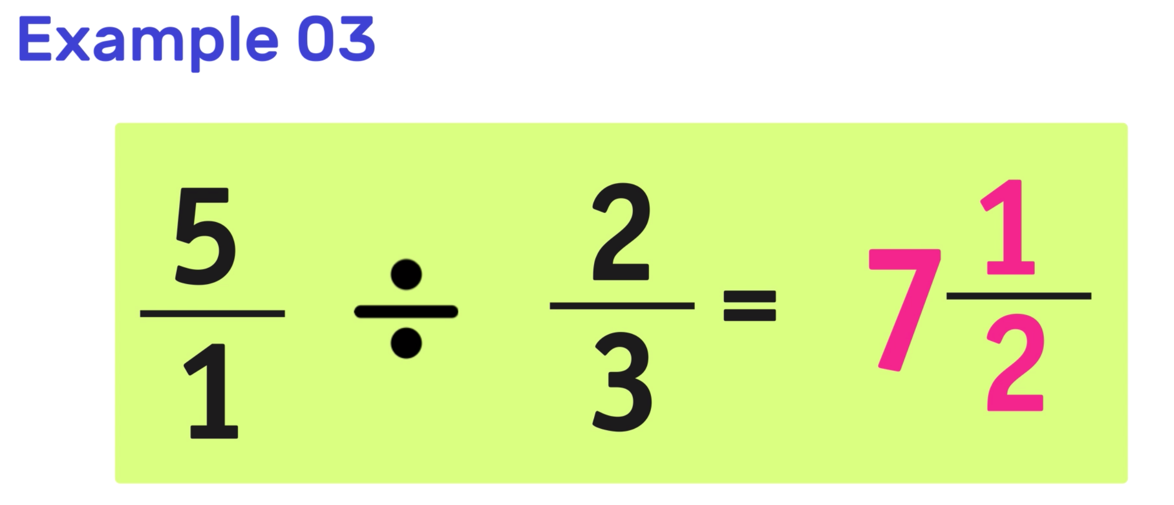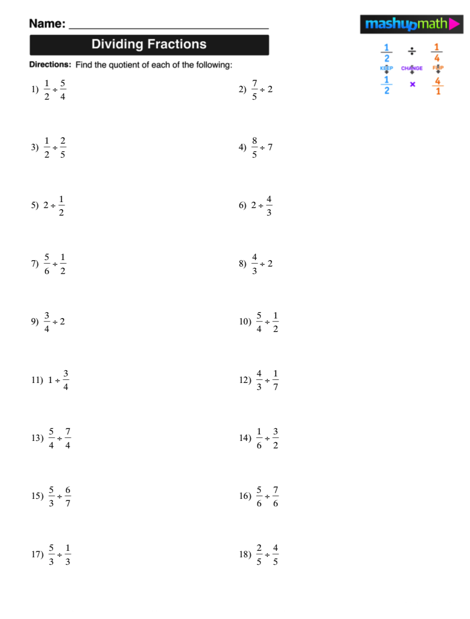Are you looking for strategies to help your kids understand equivalent fractions this school year?

Creating fraction kits is a great way to get your kids exploring equivalent fractions and acquiring a deep, conceptual understanding of the topic.

The video below demonstrates how to create a fraction kit; it was designed to serve as a follow-along activity:

Materials: construction paper, markers, scissors, and a ruler.

Looking for the corresponding lesson guide? click here to download yours

And here are some great links to more fun math activities:

• How to Convert Decimals into Fractions in 3 Easy Steps

• 4th Grade Word Problems: Free PDF Worksheets

• Check Out This Awesome Mean, Median, and Mode Activity

• 10 Super Fun Math Riddles for Kids

• Free Math Coloring Worksheets for 5th Grade

• Idea: How to Engage Your Students at the Start of Any Lesson

---

“I always look forward to getting my Mashup Math newsletter email every week. I love the free activities!” -Christina R., 5th Grade Math Teacher, Dallas, TX

Do YOU want free math resources, lesson activities, and puzzles and games for grades 1-8 in your inbox every week? Join our mailing list and start getting tons of free stuff (including a free PDF workbook)!

---

Check Out These Posts on What’s Trending in Math Education:

Bar Charts and Bar Graphs Explained!

Complete Guide: Bar Charts and Bar Graphs

Key Question: What is a bar chart? How do you read and how do you create a bar chart or bar graph?

Bar Chart Example

Welcome to this free step-by-step guide to bar charts and bar graphs. This guide will teach you how to create a bar chart from a data table and how to read a bar chart and draw conclusions from the data it represents.

Below you will find several bar graph examples that will help you to learn how to understand bar graphs.

Note that this lesson will use bar graph and bar chart interchangeably, as both terms mean the same thing.

Also, this free guide includes an animated video lesson and a free practice worksheet with a full answer key.

What is a Bar Chart? What is a Bar Graph?

A bar chart, also referred to as a bar graph, is a diagram that can be used to compare and contrast values in relation to each other.

Bar graphs include rectangular bars that are in proportion to the values that they represent.

Now, let’s take a look at our first example:

Bar Graph Example 01

How to Create a Bar Graph

Create a bar graph that represents the data chart for a student survey of favorite types of drinks.

The first step to making a bar graph is to give the bar graph a title. For this example, you can title the graph Favorite Types of Drinks.

The next step is to label the vertical and horizontal axes.

For the vertical axis, you must choose numerical units that match the data. Since all of the numbers in the table are single-digit values, you can make the vertical axis values go from zero to ten. Note that the first value on any bar graph (located in the bottom -left corner) will always be zero.

On the horizontal axis, you will include a label for each data item. In this example, each data item is a type of drink: Milk, Soda, Water, Juice, and Tea.

Now you are ready to construct your bars!

Start with the first data value, which is Milk, by constructing a bar over the Milk label that starts at zero and rises up to the number 1, which corresponds with the value for Milk in the data table.

Next, repeat this process for the other data items on the chart: Soda-3, Water-6, Juice-7, and Tea-5:

And now you made a bar graph that represents the data table.

---

Looking for More Help with Multiplying a Fraction by a Fraction? Check out this free guide

---

Bar Graph Example 02

How to Read a Bar Graph

Unlike the last example where you had to create your own bar graph, let’s get some practice reading bar graphs and drawing conclusions.

Complete the data chart and draw 3 conclusions from the bar graph below:

To complete the data chart for this bar graph, simply see which value each items bar sits at.

For example, the bar graph shows the number of pounds of radishes sold was 50 (because the vertical bar over radishes stops at 50).

Furthermore, notice that the bar graph shows the number of pounds of sweet potatoes sold is midway between 70 and 80, so we can conclude that the total number of pounds sold was 75.

Continue this process to complete the data table as follows:

The last step is to use the bar graph to draw some conclusions from the data.

For example:

• Carrots are the most sold vegetable (the bar for carrots was the highest)

• Cabbage is the least sold vegetable (the bar for cabbage was the lowest)

• 15 more pounds of sweet potatoes sold than onions sold (the bar for sweet potatoes is 15 taller than the bar for onions)

Can you draw 3 more conclusions from the bar graph on your own?

---

Still confused? Check out the animated video lesson below:

Video: Bar Graphs Explained!

Check out the video lesson below to learn more about how to read and how to create a bar graph and bar chart:

---

Bar Graphs Worksheet

Free Worksheet!

Are you looking for some extra practice with bar graphs and bar charts? Click the links below to download your free worksheets and answer key:

CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET

Tags:  bar graphs, bar charts, bar graph example, bar graph maker, bar diagram, segmented bar graph, types of bar graph, create a bar graph, types of bar graph

---

Keep Learning:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Dividing Fractions in 3 Easy Steps: Your Complete Guide

Complete Guide: Dividing Fractions

Key Question: How do you divide fractions by fractions and fractions with whole numbers?

Learn to divide fractions using 3 easy steps.

Welcome to this free step-by-step guide to dividing fractions. This guide will teach you how to use a simple three-step method called Keep-Change-Flip to easily divide fractions by fractions (and fractions by whole numbers as well).

Below you will find several examples of how to divide fractions using the Keep-Change-Flip method along with an explanation of why the method works for any math problem that involves dividing fractions. Additionally, this free guide includes an animated video lesson and a free practice worksheet with answers!

Are you ready to get started?

Dividing Fractions: Multiplication Review

Before you learn how to divide fractions using the Keep-Change-Flip method, you need to make sure that you understand how to multiply fractions together (which is even easier than dividing!).

Since multiplying fractions is typically taught before dividing fractions, you may already know how to multiply two fractions together. If this is the case, you can skip ahead to the next section.

However, if you want a quick review of how to multiply fractions, here is the rule:

Multiplying Fractions Rule: Whenever multiplying fractions together, multiply the numerators together, then multiply the denominators together as follows…

For example, 3/4 x 1/2 can be solved as follows:

---

Looking for More Help with Multiplying a Fraction by a Fraction? Check out this free guide

---

Dividing Fractions Examples!

Now that you know how to multiply fractions, you are ready to learn how to divide fractions using the simple 3-step Keep-Change-Flip method.

Let’s start with a simple example

Dividing Fractions Example 1

Example 1: What is 1/2 ÷ 1/4 ?

To solve this example (and any problem where you have to divide fractions, we are going to use the Keep-Change-Flip method)

Where:

1.) KEEP = Keep the first fraction as is and just leave it alone.

2.) CHANGE = Change the division sign to a multiplication sign.

3.) FLIP = Flip the second fraction (swap the numerator and the denominator)

These steps can be applied to example 1 as follows:

Again, after applying Keep-Change-Flip, we have transformed the original problem of 1/2 ÷ 1/4 as follows:

Now you can solve the problem by multiplying the fractions together and simplifying if necessary:

Notice that 4/2 can be simplified.

The final answer is 2, and we can conclude that the answer to the original problem is…

Final Answer: 1/2 ÷ 1/4 = 2

---

Why Does This Answer Mean?

In example 1, we concluded that 1/2 ÷ 1/4 = 2. But what does this actually mean?

If we think about 1/2 ÷ 1/4 in the form of a question: How many 1/4s are in 1/2?

And then if we visualize 1/4 and 1/2, we can clearly see that there are 2 1/4s in 1/2, which is why the final answer is 2.

---

Fraction Divided by Fraction: Example 2

Example 2: What is 2/9 ÷ 1/3 ?

Just like example 01, you can solve this problem by using the keep change flip method as follows:

1.) Keep the first fraction 2/9 as is.

2.) Change the division sign to multiplication.

3.) Flip the second fraction to turn 1/3 into 3/1

Next, perform 2/9 x 3/1 as follows and simplify the answer if you can:

In this example, 6/9 is not the final answer, since it can be reduced to 2/3

The final answer is 2/3, and we can conclude that the answer to the original problem is…

Final Answer: 2/9 ÷ 1/3 = 2/3

---

Dividing Fractions by Whole Numbers: Example 3

What if you have to divide a fraction with a whole number? It turns out the process is exactly the same as the previous examples!

Example 03: What is 5 ÷ 2/3 ?

Notice that, in this example, you are dividing a fraction with a whole number. But it is actually very easy to convert a whole number into a fraction. All that you have to do is rewrite the number as fraction where the number itself is in the numerator and the denominator is 1.

For example, 5 can be rewritten as 5/1 and this rule applies for any whole number!

Now that you have rewritten the whole number as a fraction, you can use the Keep-Change-Flip method to solve the problem.

1.) Keep the first fraction 5/1 as is.

2.) Change the division sign to multiplication.

3.) Flip the second fraction to turn 2/3 into 3/2

Finally, multiply the fractions together and simplify if possible to find the final answer as follows:

15/2 can not be simplified, however, it can be expressed as 7 & 1/2

In this example, the answer can be expressed as 15/2 or as 7 & 1/2.

And you can conclude that the answer to the original problem is…

Final Answer: 5 ÷ 2/3 = 15/2 or 7&1/2

---

Still confused? Check out the animated video lesson below:

Video: Dividing Fractions Explained!

Check out the video lesson below to learn more about how to divide fractions by fractions and fractions by whole numbers:

---

Dividing Fractions Worksheet

Free Worksheet!

Are you looking for some extra practice dividing fractions? Click the links below to download your free worksheets and answer key:

CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET

Tags:  divide fractions, dividing fractions by whole numbers, dividing fractions examples, fraction divided by fraction

---

Keep Learning:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

How to Use a Protractor: Your Complete Guide

Complete Guide: How to Use a Protractor

Key Question: How can I use a protractor to measure angles?

Learn how to solve these kinds of problems.

Welcome to this free lesson guide where you will learn how to read a protractor and how to use it to measure angles.

This complete guide on how to use a protractor includes several examples, an animated video mini-lesson, and a free worksheet and answer key.

Let’s get started!

How to Use a Protractor: Quick Review

Before we learn how to use the protractor tool to measure angles, let’s do a super quick review of angle notation (understanding this important skill will make learning how to use a protractor much easier).

Angle Notation: In geometry, an angle is denoted by the ∠ symbol and includes 3 consecutive letters which represent the three points that form the angle. Note that the middle letter denotes the vertex point of the angle.

For example, notice how in the diagram below that both angles ∠ABD and ∠CBD have point B as their vertex, but have different measures?

In this example, ∠ABD=120 and ∠CBD=60. But what happens when the angle measures are not included on the diagram? How can you find the measure of the angles in these kinds of situations?

This is where the protractor tool comes in!

---

Need some more help with naming angles?

If so, check out our short animated video lesson on how to name angles before moving forward with the protractor lesson.

Click here to watch the video on YouTube.

---

How to Use a Protractor

Now that you know understand angle notation, you are ready to learn how to use the protractor tool to find the measure of an angle.

Example: Use a protractor to find the measure of ∠MLN in the diagram below.

First, make sure that you correctly identify the angle in question. ∠MLN is the angle formed by points M, L, and N with a vertex at point L. Notice that the ∠MLN is now colored in the diagram below. If you find having the angle colored helpful, you can use markers or highlighters whenever you are using a protractor to measure angles on paper.

Quick Note: Before moving forward, identify the Center Marker on your protractor.

The next step is to line up the center marker of the protractor with the vertex point of the angle (point L in this example) as follows:

Make sure that the bottom ray of the angle (segment LN in this example) is aligned with the bottom of the protractor as shown in the diagram.

How to Read a Protractor

60 or 120?

Now that you have your protractor in position, the last step is to use it to identify the angle measure.

Remember that we are trying to find the measure of ∠MLN. In order to do this, we must identify where the top ray of the angle (segment LM in this example) intersects with the protractor and then read the measurements.

Notice that where segment LM crosses the protractor, there are two values: 60 and 120.

Since ∠MLN is an acute angle (less than 90 degrees), you know that it can not equal 120 degrees.

Therefore, the measure of ∠MLN must be 60 degrees.

---

How to Read a Protractor: More Examples

Below are a few more examples of how to read a protractor.

Example A: ∠EFT = 100

Notice that the angle in question is obtuse (>90 degrees)

Example B: ∠GFT = 80

Notice that the angle in question is acute (<90 degrees)

Example C: ∠RQS = 35

Notice that the angle in question is acute (<90 degrees)

Example D: ∠PQS = 151

Notice that the angle in question is obtuse (>90 degrees)

Example E: Right Angles

In Example D, notice that both angles in question ∠WYZ and ∠WYX are right angles, thus they are neither acute or obtuse and both have an angle measure of 90 degrees.

You probably didn’t need a protractor to identify that ∠WYZ and ∠WYX were right angles, but this example shows you how a protractor can always help you to find the measure of a give angle.

Pretty cool, right?

---

Still confused? Check out the animated video lesson below:

Video: How to Use a Protractor Explained!

Check out the video lesson below to learn more about how to measure angles using a protractor.

---

Protractor Practice Worksheet

Free Worksheet!

Are you looking for some extra practice with using a protractor to measure angles? Click the links below to download your free worksheets and answer key:

CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET

---

Keep Learning:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Free Fraction Chart (Printable PDF)

Free PDF Fraction Chart (Equivalent Fractions)

Are you looking for a useful reference chart for comparing and identify equivalent fractions?

If so, click the link below to download your free fraction chart as an easy to share and print pdf file.

Need extra practice or help working with Equivalent Fractions? Check out this free Equivalent Fractions Explained! lesson guide.

Free PDF Fraction Chart!

⤓ Download Your Free Fraction Chart PDF

---

Activity Idea: Fraction Kits

Are you looking for strategies to help your kids understand equivalent fractions this school year?

Creating fraction kits is a great way to get your kids exploring equivalent fractions and acquiring a deep, conceptual understanding of the topic.

Click here to learn more about this activity and to see a video tutorial!

---

Fraction Chart Uses

You can use the above fraction chart as a quick reference for comparing fractions and identifying equivalent fractions.

You can also use the chart to help you with adding and subtracting fractions!

We recommend printing out the chart (preferably in color and having it close by whenever you are learning about or working on problems involving fractions.

More Free Fractions Resources and Lessons:

---

Share your ideas, questions, and comments below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.