Geometry Transformations: Dilations Made Easy!

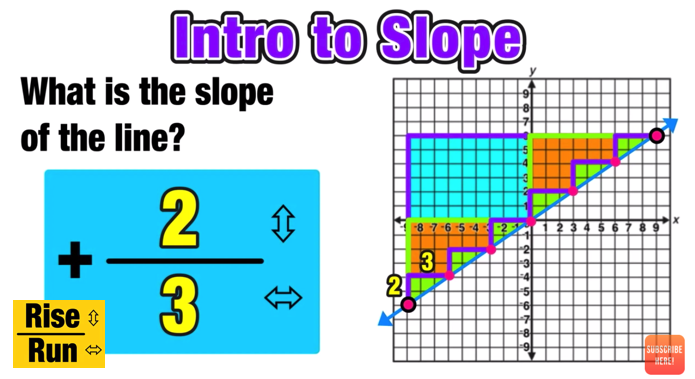
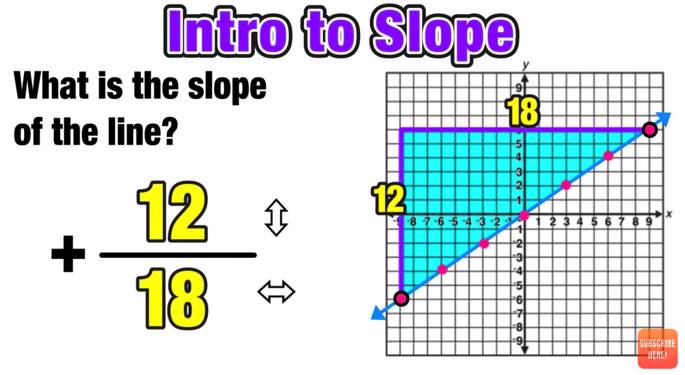
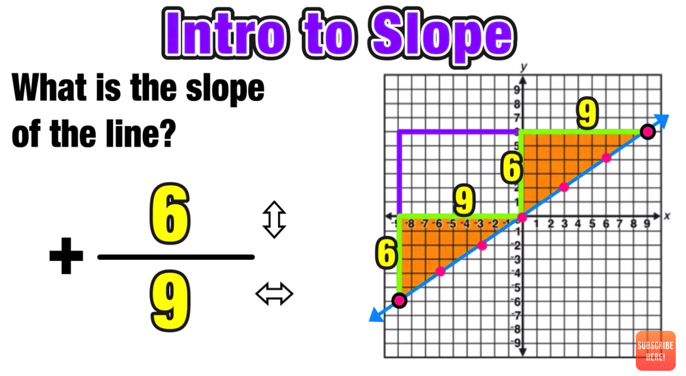
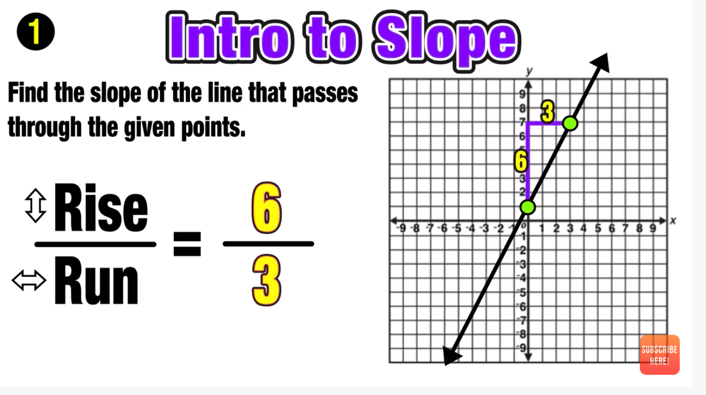
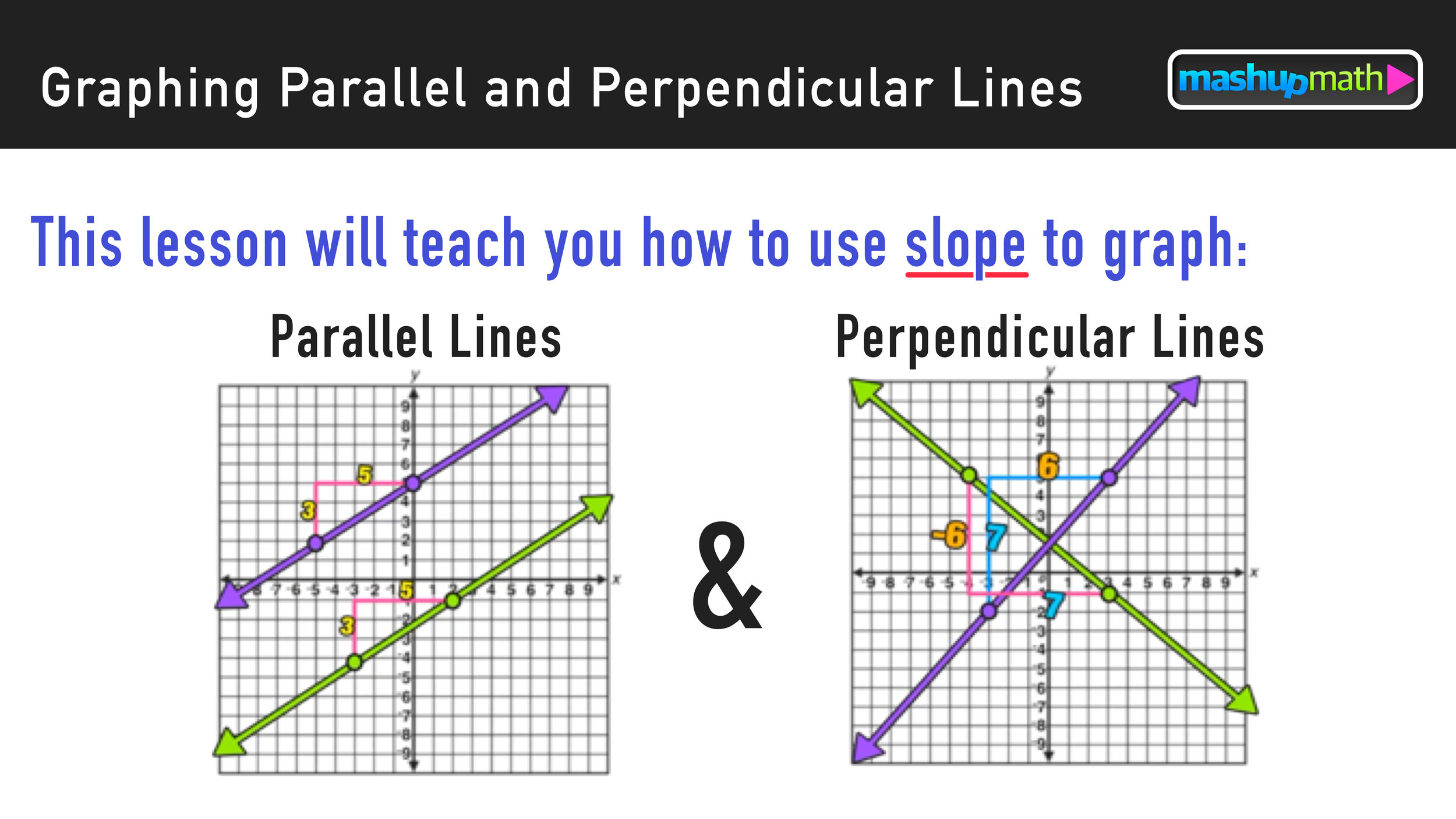
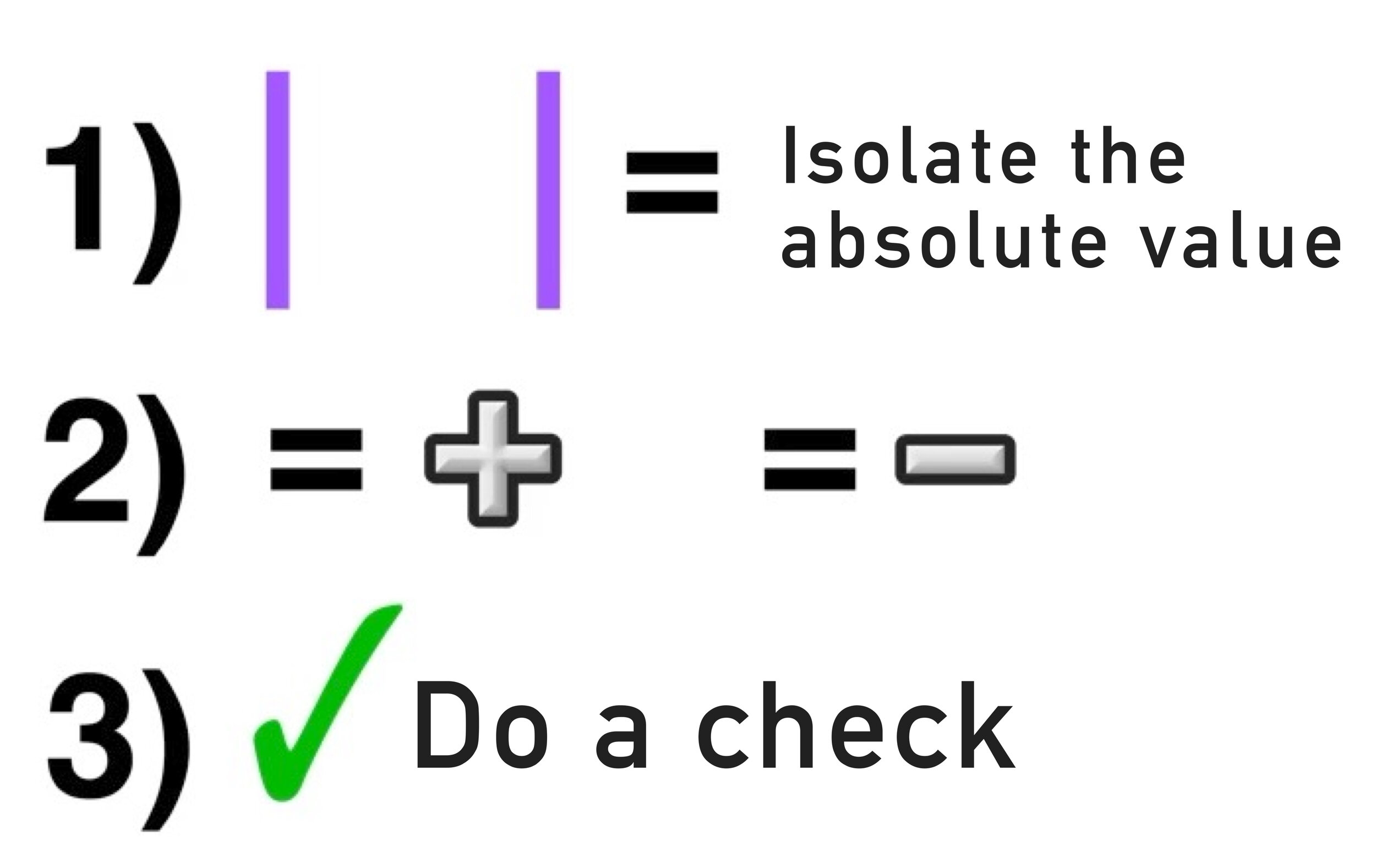
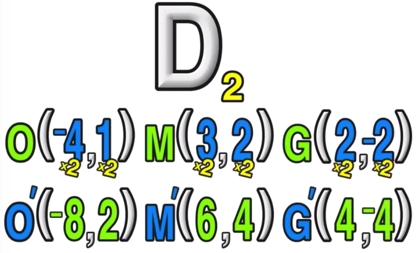Performing Geometry Dilations: Your Complete Guide

The following step-by-step guide will show you how to perform geometry dilations of figures and to understand dilation scale factor and the definition of geometry in math! (Free PDF Lesson Guide Included!)

Welcome to this free lesson guide that accompanies this Geometry Dilations Explained Video Tutorial where you will learn the answers to the following key questions and information:

• What is the geometry dilation definition and what is definition of dilation in math?

• What is a dilation scale factor?

• How can you dilate a figure like a triangle on the coordinate plane?

• Several dilation geometry examples

This Complete Guide to Geometry Dilations includes several examples, a step-by-step tutorial, a PDF lesson guide, and an animated video tutorial.

---

*This lesson guide accompanies our animated Geometry Transformations: Dilations Explained! video.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

Dilation Geometry Definition

Before you learn how to perform dilations, let’s quickly review the definition of dilations in math terms.

Dilation Geometry Definition: A dilation is a proportional stretch or shrink of an image on the coordinate plane based on a scale factor.

• Stretch = Image Grows Larger

• Shrink = Image Grows Smaller

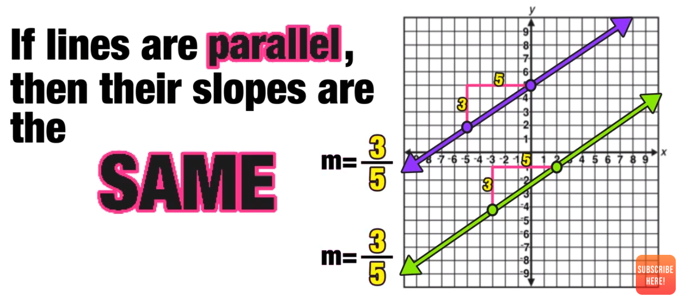
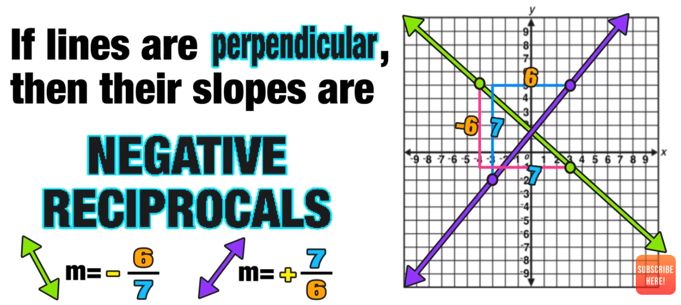
Note that a geometry dilation does not result in a change or orientation or shape!

Dilation Scale Factor

The following notation is used to denote dilations based on a scale factor of K:

K represents a number. When K=1 (the dilation scale factor is 1), the image does not change:

A scale factor one 1 is uncommon, because it doesn’t change anything!

But when K>1 (the dilation scale factor K is a number that is larger than 1), the image will be stretched!

If K=2, the image is stretched twice as large as the original!

And when K<1 (the dilation scale factor K is a number less than 1), the image will shrink. Note that the scale factor cannot be less than or equal to zero (this would completing eliminate the figure).

If K=1/2, the image shrinks to half of its original size.

When shrinking a figure, the scale factor is greater than zero, but less than one.

Now you are ready to try a few geometry dilation examples!

---

---

Geometry Dilation Examples

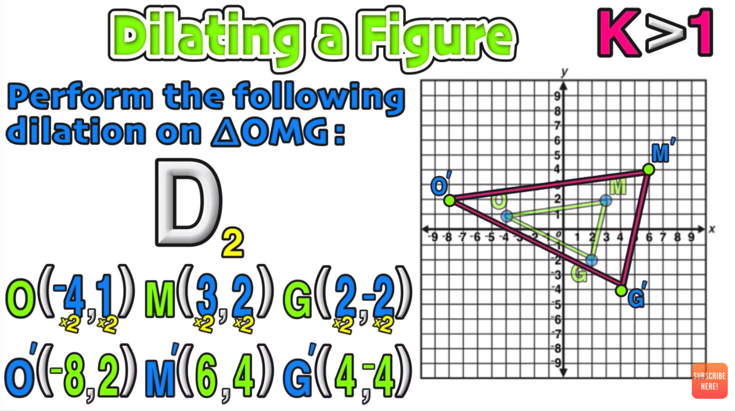
Example 1: Dilation Scale Factor >1

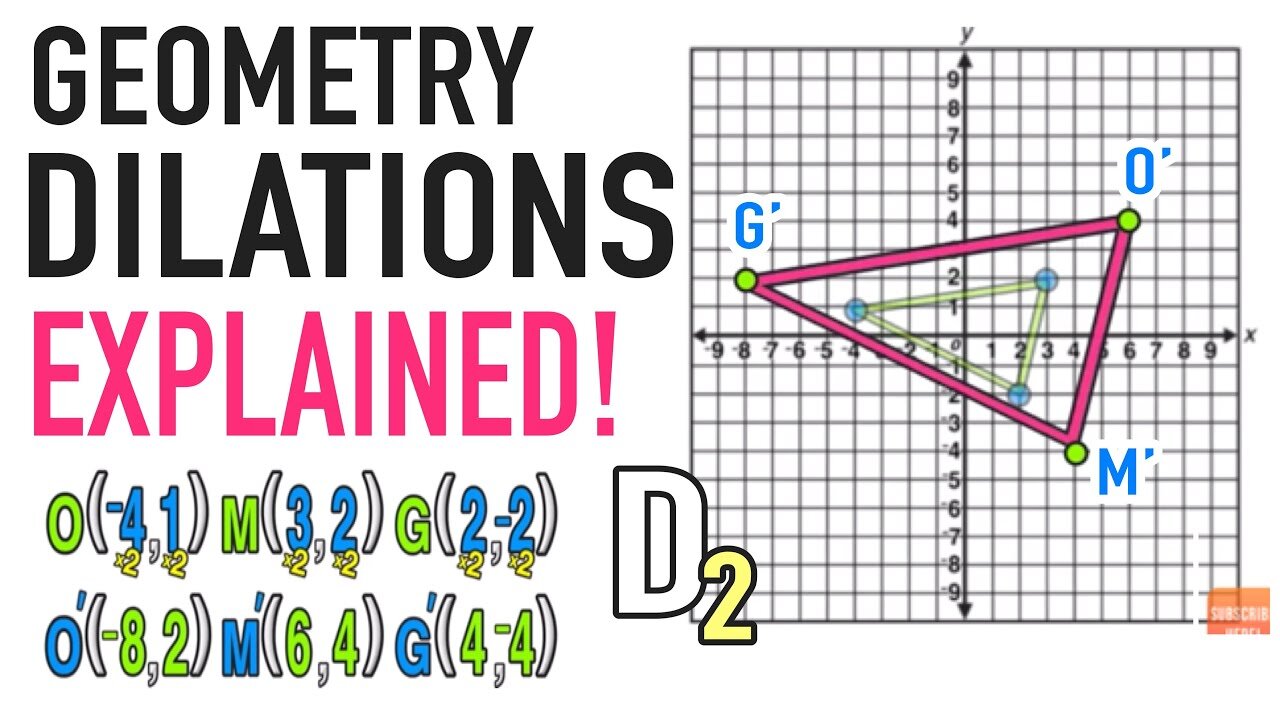
In this example, you have to dilate ▵OMG by a scale factor of 2 to create a new triangle: ▵O’M’G’.

Start by writing down the coordinates of the vertices of ▵OMG as follows:

The next step is to take the scale factor (2 in this example) and multiply it by the x and y-value of points O, M, and G, as follows:

Now you have the coordinates of O’, M’, and G’

You can now draw ▵O’M’G’ on the coordinate plane by plotting the points that you just found:

You have just constructed ▵O’M’G’, which is the image of ▵OMG after a dilation of 2.

<><><>

---

---

Example 2: Dilation Scale Factor <1

In this example, you have to dilate figure MASH by a scale factor of 1/3 to create a new figure: M’A’S’H’

Since the dilation scale factor is less than one, the new figure will be smaller version of the original (shrink).

Start by writing down the coordinates of the vertices of figure MASH as follows:

The next step is to take the scale factor (1/3 in this example) and multiply it by the x and y-value of points M, A, S, and H, as follows:

Now you have the coordinates of M’, A’, S’, and H’

You can now draw figure M’A’S’H’ on the coordinate plane by plotting the points that you just found:

You have just constructed M’A’S’H’, which is the image of MASH after a dilation of 1/3.

<><><>

---

Free Geometry Dilations Lesson Guide

Free PDF Lesson Guide

Looking for more help with geometry dilations?

Click the link below to download your free PDF lesson guide that corresponds with the video lesson below!

Click here to download the Your Free PDF Lesson Guide

Still Confused?

Check out this animated video tutorial on geometry dilations and scale factors:

---

---

Looking for more practice with Geometry Transformations?

Check out the following free resources:

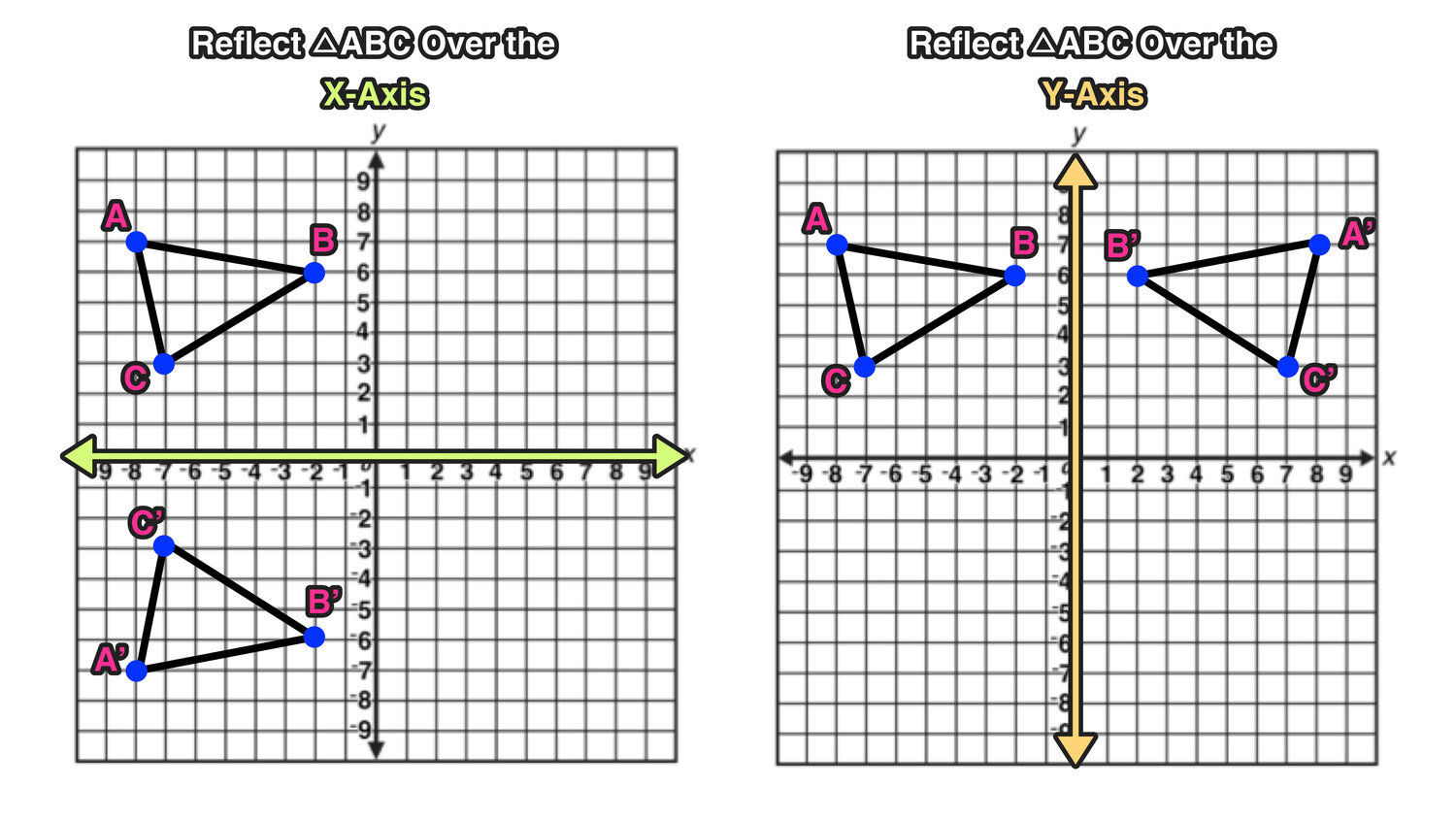
Free Tutorial on Reflections!

Reflections Over the X- and Y-Axis: Complete Guide

Video Lessons:

Geometry Rotations Explained!

Geometry Translations Explained!

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Finding Slope of a Line: 3 Easy Steps

Finding Slope of a Line in y=mx+b Form: Everything You Need to Know

Are you ready to learn how to understand and identify the slope of a line and how to find the slope of a line?

Before you learn an easy method for finding slope (with and without a calculator), let’s make sure that you understand a few basics of slope, including the slope definition.

Slope Definition:

•  The slope of a line refers to its direction and steepness.

• There are 4 kinds of slope: positive, negative, zero, and undefined. In this guide, we are only going to look at positive and negative slope. Click here to watch a video tutorial review of the 4 kinds of slope.

Note that positive slopes increase from left to right and negative slopes decrease from left to right.

Finding Slope: Rise Over Run

The slope of a line is expressed as a fraction that is commonly referred to as rise over run.

The numerator (rise) refers to how many units up or down and the denominator (run) refers to how many units left or right. The direction will depend on whether or not the slope is positive or negative.

Positive Slope: Rise Over Run

Rise: UPWARDS Run: TO THE RIGHT

Negative Slope: Rise Over Run

Rise: DOWNWARDS Run: TO THE RIGHT

How to Find the Slope of a Line: 3 Easy Steps

You can find the slope of any line by following these three easy steps:

Step One: Determine if the slope if positive (increasing) or negative (decreasing)

Step Two: Using two points on the line, calculate the rise and the run and express it as a fraction (rise over run).

Step Three: Simplify the fraction if possible.

Let’s take a look at a few examples!

EXAMPLE: Find the slope of the line below.

Step One: Determine if the slope if positive (increasing) or negative (decreasing)

Notice that the line is increasing from left to right, so we know that this line has a positive slope!

Step Two: Using two points on the line, calculate the rise and the run and express it as a fraction (rise over run).

For this example, let’s start by choosing the left farthest point (-9,-6) and the right farthest point (9,6).

To find rise over run, draw a vertical line that rises from (-9,6) and a horizontal line that runs to (9,6), then count how many units you had to travel upward (rise) and how many to the right (run) and express it as a fraction as follows:

Rise over run is like building a staircase!

Step Three: Simplify the fraction if possible.

Right now, you can say that the slope of the line is 12/18. But 6/9 is also equivalent to 12/18, so let’s see what that would look like on the graph by starting from the first point (-9,-6) and this time rising up 6 and running to the right 9 units repeatedly as follows:

Notice how you end up in the same spot!

At this point, it is clear that the line has a slope of 12/18 and a slope of 6/9.

But we don’t want to have multiple slopes for the same line, so you will always express the slope of a line in simplest or reduced form.

In this example, the slopes of 12/18 and 6/9 can be simplified to 2/3 as follows:

And since 2/3 can not be simplified further, you can conclude that:

Final Answer: The line has a slope of positive 2/3

---

---

Finding Slope of a Line Examples

EXAMPLE #1: Find the Slope of the Line

View fullsize

Step One: Determine if the slope if positive (increasing) or negative (decreasing)

Notice that the line is increasing from left to right, so we know that this line has a positive slope!

Step Two: Using two points on the line, calculate the rise and the run and express it as a fraction (rise over run).

In this example, use the two given points as follows:

The rise is 6 and the run is 3.

Step Three: Simplify the fraction if possible.

You should know that 6/3 is equal to 2 (six divided by three). Since we want to think about slope as the fraction rise over run, we can express 2 as 2/1:

Notice that 6/3 reduces to 2/1 or just 2.

You can see that 2/1 is equivalent to 6/3 since the pink staircase on the graph above still gets you to the same point.

So now you can express your answer as follows:

Final Answer: The line has a slope of positive 2.

---

---

Finding Slope of a Line Examples

EXAMPLE #2: Find the Slope of the Line

Step One: Determine if the slope if positive (increasing) or negative (decreasing)

Notice that the line is decreasing from left to right, so we know that this line has a negative slope!

Step Two: Using two points on the line, calculate the rise and the run and express it as a fraction (rise over run). Remember that you have to rise down when dealing with negative slopes.

In this example, use the two given points as follows:

The slope is negative!

Step Three: Simplify the fraction if possible.

Notice that the fraction -3/8 can not be simplified further, so you can conclude that:

Final Answer: The line has a slope of - 3/8.

---

Looking to Learn More About Slope?

Check out these free video tutorials:

Free Slope Calculator

If you need a fast and easy way to find the slope of a line, then you can take advantage of the many free online slope calculators that are available.

This free slope calculator from calculator.net not only finds slope but it expresses it in reduced form and includes whether the slope is positive or negative.

To use the slope calculator, simply input the x and y-values for any two points on the line and press calculate.

Finding Slope of a Line Worksheet

Do you need more practice with finding the slope of a line? The following finding slope worksheet and answer key will give you plenty of opportunities to practice using the three-step process!

Click here to download your free Finding Slope Worksheet with Answers.

And if you are looking for a more in-depth lesson on how to find the slope of a line, check out this free Finding Slope Video Lesson:

Read More Posts About Math Education:

---

Share your ideas, questions, and comments below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Parallel Slopes and Perpendicular Slopes: Complete Guide

Finding Slopes of Parallel and Perpendicular Lines (and Graphing): Complete Guide

The following step-by-step guide will show you how to use parallel slope and perpendicular slope to graph parallel and perpendicular lines

Welcome to this free lesson guide that accompanies this Graphing Parallel and Perpendicular Lines Using Slope Tutorial where you will learn the answers to the following key questions and information:

• What is parallel slope?

• What is perpendicular slope?

• How can I graph parallel lines?

• How can I graph perpendicular lines?

This Complete Guide to Parallel and Perpendicular Lines and Slope includes several examples, a step-by-step tutorial and an animated video tutorial.

---

*This lesson guide accompanies our animated Graphing Parallel and Perpendicular Lines Using Slope video.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

Parallel Slope and Perpendicular Slope

Before you learn how to graph parallel and perpendicular lines, let’s quickly review some important information:

Parallel Lines

• Never intersect

• Have the SAME SLOPE (m)

For example, observe the purple line and the green line in Figure 1 below. These lines are parallel and have the same slope of m=3/5.

This is true for all parallel lines.

Figure 1

Perpendicular Lines

• Intersect to Form Right Angles

• Have the NEGATIVE RECIPROCAL SLOPES (m)

For example, observe the purple line and the green line in Figure 2 below. These lines are perpendicular and have negative reciprocal slopes.

Another way of saying negative reciprocal is FLIP AND SWITCH, which means to take the slope of the first line, flip the fraction and switch the sign (positive to negative or vice versa).

In this case, the green line slope is -(6/7) and the purple line slope is +(7/6)

This is true for all perpendicular lines.

Figure 2

Parallel Slope Example

Example:

Let’s start by identifying the key information:

Since you have to graph a line through point J that is PARALLEL to line S, then you know that you will be dealing with SAME SLOPE.

Start by finding the slope of line S by finding the slope between the two given points (-4,0) and (5,2). You can find the slope by counting “rise over run” or by using the slope formula.

In this example, Line S has a slope of m=2/9.

Again, since parallel lines have the same slope, you can build your new line through point J by repeating the slope m=2/9 starting at point J as follows:

Now that you have plotted a new point using the same slope, the final step is to construct a line that passes through the new point and point J as follows:

And you have graphed your parallel line using slope!

---

---

Perpendicular Slope Example

Example:

Figure 1

Start by identifying the key information.

Since you have to graph a line through point K that is PERPENDICULAR to line T, then you know that you will be dealing with NEGATIVE RECIPROCAL SLOPES (also known as “flip and switch”).

Start by finding the slope of line T by finding the slope between the two given points (-3,-1) and (-1,7). You can find the slope by counting “rise over run” or by using the slope formula.

In this example, Line T has a slope of m= +8/2, which simplifies to m=+4/1

Now that you know that the slope of Line T is m=+(4/1), you are ready to find the slope of the new line by finding the negative reciprocal.

You can do this taking the slope of Line T and doing “flip and switch”.

To do this, flip the fraction and switch the sign as follows:

The las step is to use the negative reciprocal to build your new line. You can do this by starting at point K and going down one unit and to the right four units (rise: -1, run: +4) and then plot a new point.

Now that you have plotted a new point using the negative reciprocal slope, the final step is to construct a line that passes through the new point and point K as follows:

And you have graphed your parallel line using slope!

---

---

Still Confused?

Check out this animated video tutorial on slopes of parallel and perpendicular lines and graphs:

---

---

Looking for more practice with graphing and slope?

Check out the following free resources:

Free Tutorial

Intro: Slope of a Line in Y=MX+B Form

Finding the Equation of a Line Using Two Points!

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Finding the Inverse of a Function: Complete Guide

Learn How to Find the Inverse of a Function Using 3 Easy Steps

The following step-by-step guide will show you how to find the inverse of any function! (Algebra)

Welcome to this free lesson guide that accompanies this Finding the Inverse of a Function Tutorial where you will learn the answers to the following key questions and information:

• What is the inverse of a function?

• What does the graph of the inverse of a function look like?

• How can I find the inverse of a function algebraically?

• How can I find the inverse of a function graphically?

This Complete Guide to Finding the Inverse of a Function includes several examples, a step-by-step tutorial and an animated video tutorial.

---

*This lesson guide accompanies our animated How to Find the Inverse of a Function in 3 Easy Steps video.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

Intro to Finding the Inverse of a Function

Before you work on a find the inverse of a function examples, let’s quickly review some important information:

Notation: The following notation is used to denote a function (left) and its inverse (right). Note that the -1 use to denote an inverse function is not an exponent.

What is a function?

By definition, a function is a relation that maps X onto Y.

And what is the inverse of a function?

An inverse function is a relation that maps Y onto X.

Notice the switch?

You can think of the relationship of a function and its inverse as a situation where the x and y values reverse positions.

For example, let’s take a look at the graph of the function f(x)=x^3 and its inverse.

Take a look at the table of the original function and its inverse. Notice how the x and y columns have reversed!

Definition: The inverse of a function is its reflection over the line y=x.

Keep this relationship in mind as we look at an example of how to find the inverse of a function algebraically.

Finding the Inverse of a Function Example

We will be using the following 3-step process that can be used to find the inverse of any function:

STEP ONE: Rewrite f(x)= as y=

If the function that you want to find the inverse of is not already expressed in y= form, simply replace f(x)= with y= as follows (since f(x) and y both mean the same thing: the output of the function):

STEP ONE: Swap X and Y

Now that you have the function in y= form, the next step is to rewrite a new function using the old function where you swap the positions of x and y as follows:

Original Function

New inverse function!

This new function with the swapped X and Y positions is the inverse function, but there’s still one more step!

STEP THREE: Solve for y (get it by itself!)

The final step is to rearrange the function to isolate y (get it by itself) using algebra as follows:

It’s ok the leave the left side as (x+4)/7

Once you have y= by itself, you have found the inverse of the function!

Final Answer: The inverse of f(x)=7x-4 is f^-1(x)=(x+4)/7

---

---

Graphs of Inverse Functions

Remember earlier when we said the inverse function graph is the graph of the original function reflected over the line y=x? Let’s take a further look at what that means using the last example:

Below, Figure 1 represents the graph of the original function y=7x-4 and Figure 2 is the graph of the inverse y=(x+4)/7

Figure 1

Figure 2

Now let’s take a look at both lines on the same graph. Note that the original function is blue and the inverse is red this time (Figure 3) and then add the line y=x to the same graph (Figure 4).

Figure 3

Figure 4

Can you see the reflection over the line y=x?

This relationship applies to any function and its inverse and it should help you to understand why the 3-step process that you used earlier works for finding the inverse of any function!

---

Still Confused?

Check out this animated video tutorial on how to find the inverse of any function!

---

---

Looking for more practice with functions?

Check out the following free resources:

Free Tutorial

The Parent Function Graphs and Transformations!

How to Graph a Quadratic and Find Intercepts, Vertex, & Axis of Symmetry!

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Solving Absolute Value Equations: Complete Guide

Learn How to Solve Absolute Value Equations in 3 Easy Steps!

The following step-by-step guide will show you how to solve absolute value equations and absolute value functions with ease (Algebra)

Welcome to this free lesson guide that accompanies this Solving Absolute Value Equations Tutorial where you will learn the answers to the following key questions and information:

• How to solve an absolute value equation

• How to solve an absolute value function

• How to find both solutions to an absolute value equation

• Why is absolute value always positive?

This Complete Guide to Solving Absolute Value Equations includes several examples, a step-by-step tutorial and an animated video tutorial.

---

*This lesson guide accompanies our animated Solving Absolute Value Equations Explained! video.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

Intro to Solving Absolute Value Equations

Before you work on a few absolute value equations examples, let’s quickly review some important information:

Fact: Any value inside of absolute value bars represents either a positive number or zero.

Notice that the absolute value graph in Figure 1 has a range of y is greater than or equal to 0 (it is never negative)

Figure 1: The parent function for absolute value.

Furthermore, consider the example below:

There are two values that would make this equation true!

The absolute value of 5 AND the absolute value of -5 both equal positive 5.

This should make sense when you graph the line y=5 over the absolute value function graph because you can see that there are two intersection points, and thus two solutions.

Absolute value functions can have up to two solutions!

Now you know that ABSOLUTE VALUE EQUATIONS CAN HAVE TWO SOLUTIONS.

Now you are ready to try a few examples.

Solving Absolute Value Equations Example #1

We will be using the following 3-step process that can be used to solve any absolute value equation:

STEP ONE: Isolate the Absolute Value

In this example, the absolute value is already isolated on one side of the equals sign, which means that there are no other terms outside of the absolute value, so you can move onto step two.

STEP TWO: Solve for Positive AND Solve for Negative

For step two, you have to take the original equation |x+3| = 6 and split it up into two equations, one equal to POSITIVE 6 and the other equal to NEGATIVE 6. You also get rid of the absolute value bars.

Set up two equations (positive and negative) and ditch the absolute value bars.

Now you just have to solve each equation for x as follows:

And now you have concluded that there are two solutions to |x+3|=6, x=3 and x=-9.

STEP THREE: Check Your Answer

Finally, do a quick check by plugging both answers into the original equation, |x+3|=6, to make sure that they are correct:

Left: replace x with 3. Right: replace x with -9

Both equations are true.

Since the checks worked out, you can conclude that:

Final Answer: The solutions to |x+3|=6 are x=3 and x=-9

---

---

Solving Absolute Value Equations Example #2

Again, you will follow the three-step process to solving this absolute value equation:

STEP ONE: Isolate the Absolute Value

Unlike the last example, the absolute value is not already isolated on one side of the equal sign, because there is a +8 outside of it that needs to be moved to the other side as follows:

Step One: Isolate the absolute value!

Now the absolute value is isolated.

Now that you have isolated the absolute value on one side of the equal sign, you are ready for the next step.

STEP TWO: Solve for Positive AND Solve for Negative

The next step is to ditch the absolute value bars and solve the following equations:

Positive: 2x-4=2 and Negative: 2x-4=-2

Now you have TWO solutions: x=3 and x=1

STEP THREE: Check Your Answer

The final step is to plug both solutions, x=3 and x=1, into the original equation |2x-4|+8=10 and verify that each solution checks out and you are finished!

Go ahead and check the solution to Example 2 on your own! Did it work out?

---

Still Confused?

Check out this animated video tutorial on solving absolute value equations!

---

---

Looking for more practice with absolute value?

Check out the following free cube root resources:

Free Tutorial

Absolute Value Calculator Basics: How to Graph and Solve Absolute Value Equations

How to Find X and Y Intercepts of a Function Explained!

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.