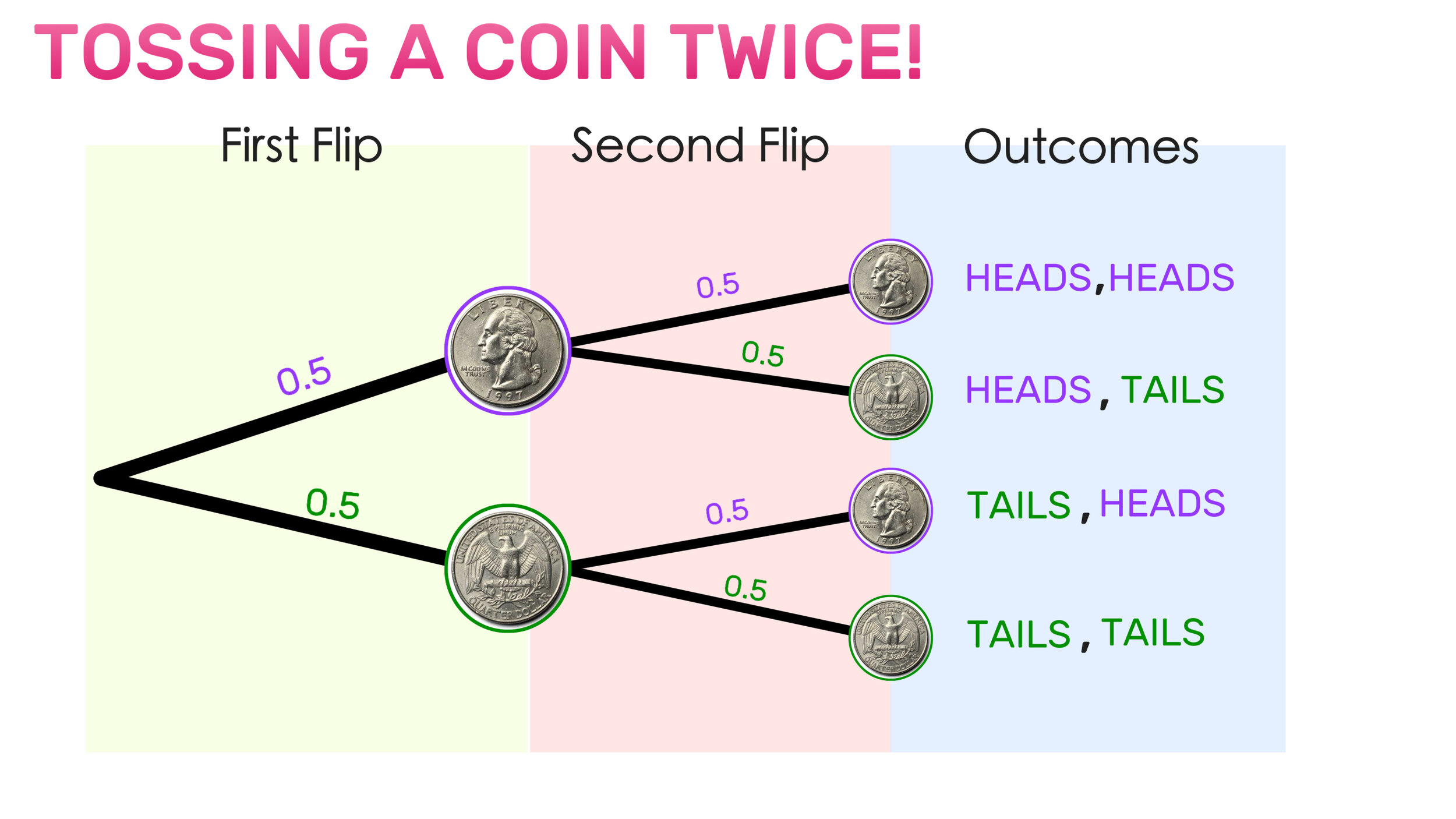
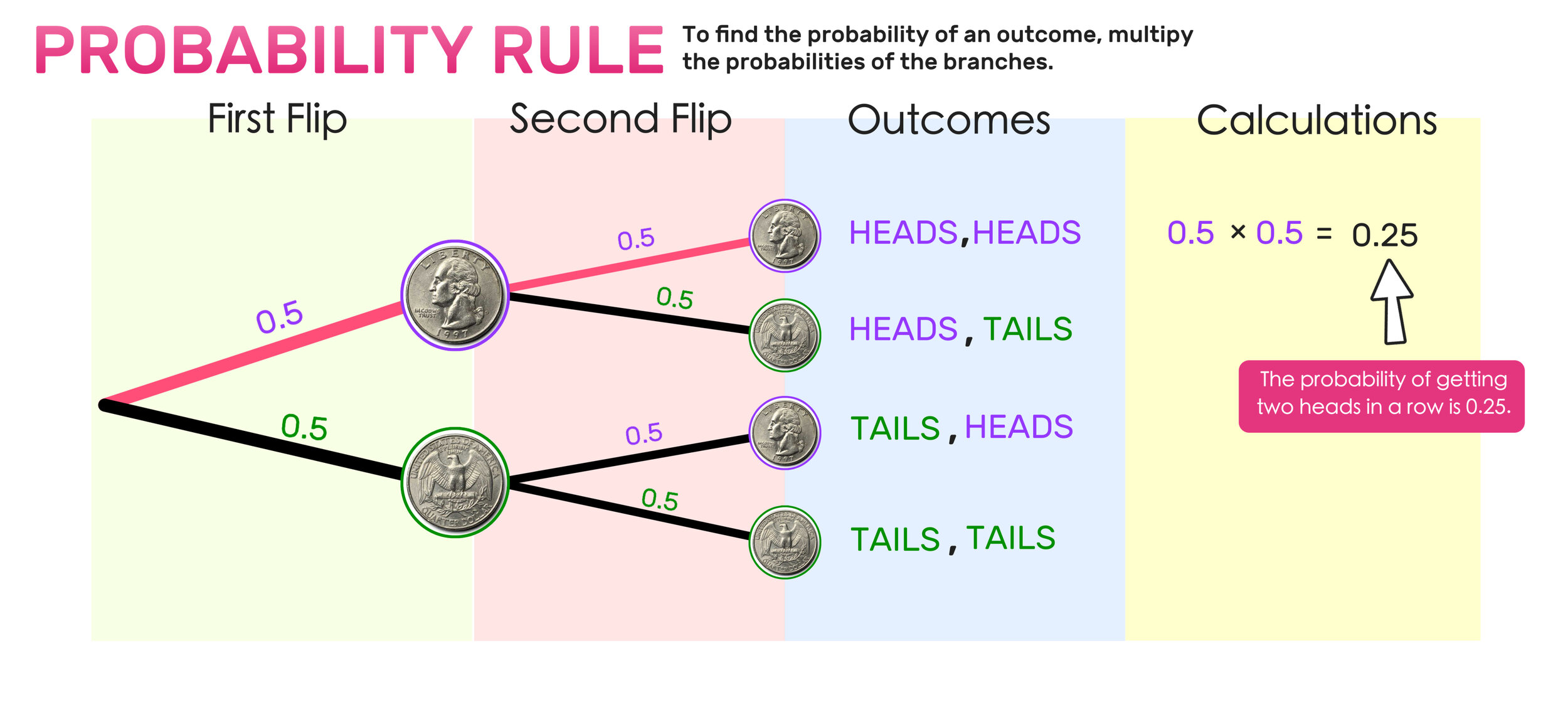
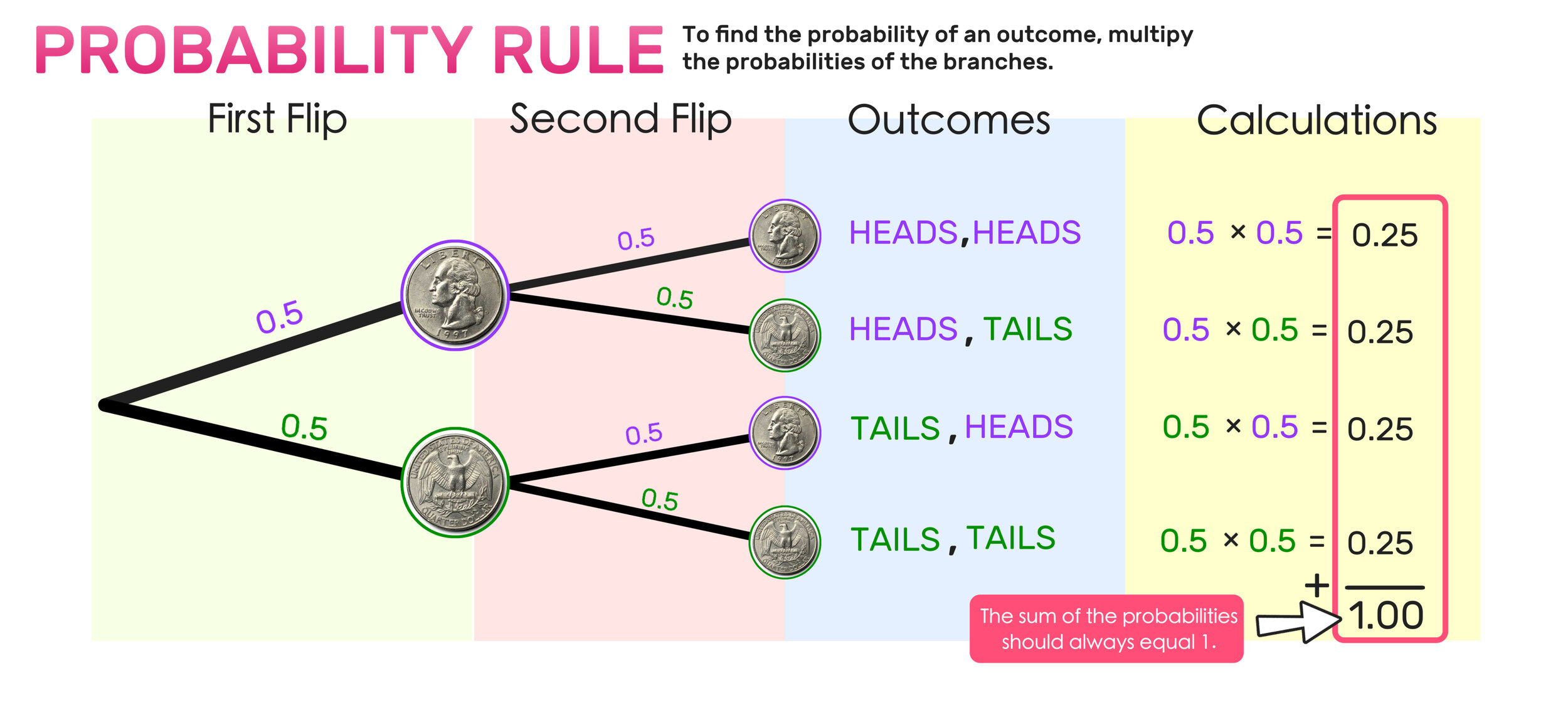
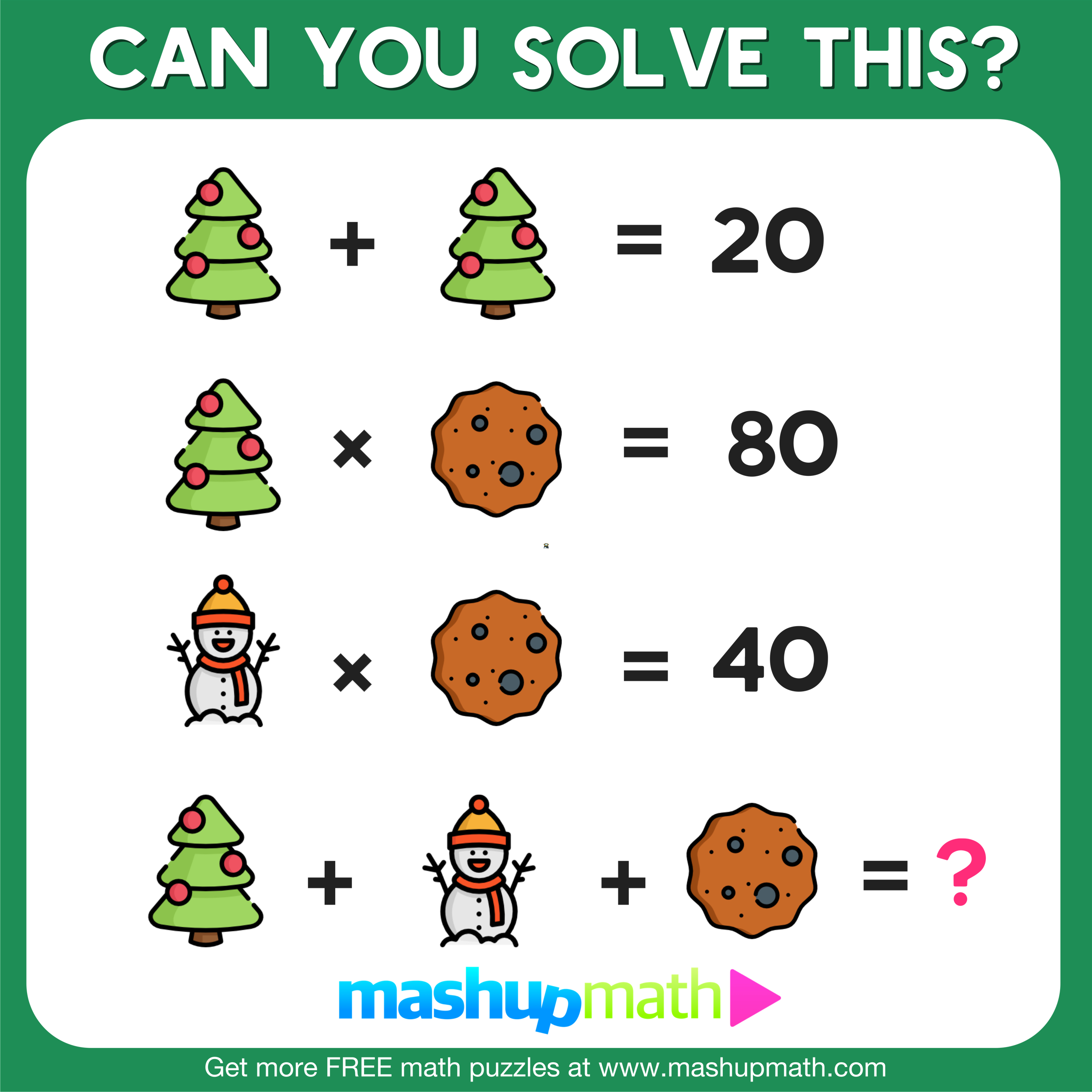PEMDAS Meaning Explained with Examples

PEMDAS Meaning: What is PEMDAS, How is it Used, and Is It Reliable?

A Post By: Anthony Persico

In mathematics, there is something called the order of operations, which is a rule for solving math problems that have more than one operation (adding, subtracting, multiplying, etc.). When studying math and learning how to correctly use the order of operations, many people rely on a common mnemonic known as PEMDAS as a memory aid for remembering the order of operations.

View fullsize

PEMDAS Meaning:

P=Parenthesis

E=Exponents

M=Multiplication

D=Division

A=Addition

S=Subtraction

These operations are meant to be performed from left to right, where the left-most operation is performed first. But this is only a general rule for remembering the order of operations and there are key nuances to the relationship between multiplication/division and addition/subtraction that must be remembered in addition to the mnemonic, PEMDAS, otherwise, it becomes a very unreliable tool that will often lead to getting wrong answers to seemingly math problems. These key nuances are highlighted in the sample section below.

PEMDAS Meaning: Key Ideas

PEMDAS has been around for a long time and many math students learn the phrase “Please Excuse My Dear Aunt Sally” as a trick to remembering the order of operations in math.

However, PEMDAS is not a perfect mnemonic for remembering how to correctly perform the order of operations, but it can be a useful tool proved that you remember a few extremely important nuances:

• Always perform parenthesis and/or groups first

• After parenthesis and groupings, perform exponents

• After parenthesis and exponents, perform multiplication/division (whichever comes first moving from left to right)

• After multiplication/division, perform addition and/or subtraction (whichever comes first moving from left to right)

PEMDAS Meaning: Examples

 It is one thing to remember the order of operations, and a completely task to know how to use it to solve math problems correctly. In fact, many old-timers can easily recall the phrase “Please Excuse My Dear Aunt Sally” decades after grade school, but have no idea what the PEMDAS meaning is or how to use it properly.

 Again, PEMDAS is only useful as a mnemonic if you also remember the previously mentioned key ideas and nuances. Now, let’s look at a few examples of how to correctly use PEMDAS to perform the order of operations.

PEMDAS Example 01: (3+1) x 4

Solve what is inside the parentheses first. In this case, 3+1=4.

 Then perform multiplication: 4 x 4 = 16

PEMDAS Example 02: 27 ÷ (8-5)^2

 Just like the last example, solve what is inside the parentheses first. In this case, 8-5 = 3.

Then move onto the exponents 3^2=9. Finally, 27÷3 = 9

PEMDAS Example 03: 10 x 6 + 1

For starters, when there are no parentheses/groupings and/or exponents, you can skip the P and the E of PEMDAS.

According to PEMDAS, you have to perform multiplication/division before addition/subtraction, so you can go ahead and solve this problem from left to right:

 10x6 = 60 and 60 + 1 = 61

PEMDAS Example 04: 75 - 10 x 5

Again, PEMDAS requires you to perform multiplication/division before addition/subtraction, so, in this example; you do not perform operations from left to right.

In this case, first perform 10 x 5 = 50, and then perform 75 – 50 = 25.

---

PEMDAS Example 05: 8 x 8 ÷ 16

This example highlights where the key nuances to PEMDAS make a huge difference. Remember that PEMDAS requires you to solve Multiplication/Division from left to right based on whichever comes first.

In this example, when moving from left to right, multiplication comes first so you would first perform 8 x 8 = 64.

Next, you would perform the division: 64 ÷ 16 = 4

Note: If you strictly followed PEMDAS moving from left to right in this example, you would have ended up with the correct answer, but let’s take a look at an example when division comes first, and multiplication comes second.

PEMDAS Example 06: 42 ÷ 7 x 3

In order to solve this problem correctly, you have to remember that a key nuance of the PEMDAS meaning is that you perform multiplication/division and addition/subtraction based on which operation comes first left to right.

 Just because M (Multiplication) comes before D (Division) in PEMDAS, doesn’t mean that you always perform multiplication first.

In this example, notice that the only two operations are division and multiplication. Unlike the last example, division comes first this time, so you have to perform 42÷7=6 first and then 6x3=18 second.

Note: Many students fail to use PEMDAS correctly in these kinds of examples and perform multiplication first 42 / 21 = 2. Note that 2 is not the correct answer.

---

PEMDAS Meaning: Why Is It Important

Correctly applying the order of operations and using PEMDAS has become very popular in recent years due to viral math problems that pop up on social media. These kinds of posts are popular because individuals assume that the correct way to apply the order of operations is to perform each operation from left to right. Since most people get these seemingly simple math problems incorrect, they are encouraged to comment and share, which rapidly spreads the post in a viral nature.

However, if individuals could remember (A) the order of operations using a mnemonic like PEMDAS (or an even more useful one known as GEMS) and (B) the nuances to correctly applying the order of operations (namely the relationship between multiplication/division and addition/subtraction), then these kinds of viral problems could be easily solved without much controversy.

PEMDAS Meaning: Conclusion

 PEMDAS is a prevalent, yet only somewhat useful mnemonic for remembering the order of operations in math. PEMDAS refers to the order of operations as follows: Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction. While many individuals remember PEMDAS using the famous phrase “Please Excuse My Dear Aunt Sally,” they often forget the important nuance that multiplication is not automatically performed before division and addition is not automatically performed before subtraction (multiplication/division and addition/subtraction are performed from left to right based on whichever operation comes first). This common misunderstanding devalues PEMDAS as a reliable memory tool and is the root cause of seemingly simple math problems going viral on social media because a large percentage of adults can remember the mnemonic decades after grade school, but can not get a correct answer.

PEMDAS has persisted as a go-to strategy for remembering the order of operations more because of nostalgia and resistance to change rather than it being the most effective strategy. And while using mnemonics is rarely a good strategy for understanding math concepts and developing reasoning skills, there are much better alternatives to PEMDAS, including GEMS, that are significantly more reliable.

---

Are you looking for a more effective and easier alternative to relying on PEMDAS?

Why is GEMS the Best Way to Teach Order of Operations?

View fullsize

---

More Free Math Resources for Grades K-8:

Free Penguin Awareness Day Math Activities for Grades K-8

Celebrate Penguin Awareness Day in Your Math Classroom

Free Penguin-Themed ‘Which One Doesn’t Belong?"‘ Math Activities for Grades K-8.

Did you know that January 20th is Penguin Awareness Day?

This international holiday celebrates everyone’s favorite flightless birds and draws attention to conserving their at-risk habitat.

You can celebrate at home by learning some new fun facts about penguins.

And you can celebrate in your classroom with three brand new Penguin-Themed ‘Which One Doesn’t Belong?’ Math Activities for students in Grades K-6.

If you’re not familiar with using ‘Which One Doesn’t Belong?’ (WODB) activities and why they are amazing for boosting student engagement in the math classroom, click here to learn everything you need to know.

I started sharing WODB activities with my students because I was struggling to find ways to get all of my students engaged, especially those who struggle with mathematics and are reluctant to participate.

The results? My student engagement skyrocketed! Since WODB activities don’t have a single correct answer (the idea is to get students thinking mathematically and learn how to justify their answers), all of my students (even ones who rarely participate) felt comfortable sharing and getting involved.

Now I use WODB at least once a week!

Again, if you want more information on how WODB activities work and how you can use them to boost student engagement in your classroom, click here to learn everything you need to know.

1.) Penguin Day WODB for Grades K-6

2.) Penguin Day WODB for Grades 4-8

*Remember that WODB activities purposely do not have a single correct answer. Click here to learn more.

3.) Bonus! Penguin Day Order of Operations Puzzles

Grades K-2

Grades 3-5

Grades 6-8+

---

These puzzles are samples from the best-selling workbook 101 Daily ‘Which One Doesn’t Belong?’ Math Activities for Grades 3-8.

You Might Also Like…

---

I am interested in…

---

Probability Tree Diagrams Explained!

Probability Tree Diagrams: Step-by-Step

This quick introduction will teach you how to calculate probabilities using tree diagrams.

Figuring out probabilities in math can be confusing, especially since there are many rules and procedures involved. Luckily, there is a visual tool called a probability tree diagram that you can use to organize your thinking and make calculating probabilities much easier.

At first glance, a probability tree diagram may seem complicated, but this page will teach you how to read a tree diagram and how to use them to calculate probabilities in a simple way. Follow along step-by-step and you will soon become a master of reading and creating probability tree diagrams.

---

What is a Probability Tree Diagram?

Example 01: Probability of Tossing a Coin Once

Let’s start with a common probability event: flipping a coin that has heads on one side and tails on the other:

View fullsize

This simple probability tree diagram has two branches: one for each possible outcome heads or tails. Notice that the outcome is located at the endpoint of a branch (this is where a tree diagram ends).

Also, notice that the probability of each outcome occurring is written as a decimal or a fraction on each branch. In this case, the probability for either outcome (flipping a coin and getting heads or tails) is fifty-fifty, which is 0.5 or 1/2.

Example 02: Probability of Tossing a Coin Twice

Now, let’s look at a probability tree diagram for flipping a coin twice!

Notice that this tree diagram is portraying two consecutive events (the first flip and the second flip), so there is a second set of branches.

Using the tree diagram, you can see that there are four possible outcomes when flipping a coin twice: Heads/Heads, Heads/Tails, Tails/Heads, Tails/Tails.

And since there are four possible outcomes, there is a 0.25 (or ¼) probability of each outcome occurring. So, for example, there is a 0.25 probability of getting heads twice in a row.

How to Find Probability

The rule for finding the probability of a particular event in a probability tree diagram occurring is to multiply the probabilities of the corresponding branches.

For example, to prove that there is 0.25 probability of getting two heads in a row, you would multiply 0.5 x 0.5 (since the probability of getting a heads on the first flip is 0.5 and the probability of getting heads on the second flip is also 0.5).

0.5 x 0.5 = 0.25

Repeat this process on the other three outcomes as follows, and then add all of the outcome probabilities together as follows:

Note that the sum of the probabilities of all outcomes should always equal one.

From this point, you can use your probability tree diagram to draw several conclusions such as:

·       The probability of getting heads first and tails second is 0.5x0.5 = 0.25

·       The probability of getting at least one tails from two consecutive flips is 0.25 + 0.25 + 0.25 = 0.75

·       The probability of getting both a heads and a tails is 0.25 + 0.25 = 0.5

Independent Events and Dependent Events

What is an independent event?

Notice that, in the coin toss tree diagram example, the outcome of each coin flip is independent of the outcome of the previous toss. That means that the outcome of the first toss had no effect on the probability of the outcome of the second toss. This situation is known as an independent event.

 What is a dependent event?

Unlike an independent event, a dependent event is an outcome that depends on the event that happened before it. These kinds of situations are a bit trickier when it comes to calculating probability, but you can still use a probability tree diagram to help you.

Let’s take a look at an example of how you can use a tree diagram to calculate probabilities when dependent events are involved.

---

Looking for a fun hands-on activity for exploring probability in math?

Activity Idea: Constructing Probability Models Using Candy!

---

How to Make a Tree Diagram

Example 03:

Greg is a baseball pitcher who throws two kinds of pitches, a fastball, and a knuckleball. The probability of throwing a strike is different for each pitch:

·       The probability of throwing a fastball for a strike is 0.6

·       The probability of throwing a knuckleball for a strike 0.2

Greg throws fastballs more frequently than he throws knuckleballs. On average, for every 10 pitches he throws, 7 of them are fastballs (0.7 probability) and 3 of them are knuckleballs (0.3 probability).

So, what is the probability that the pitcher will throw a strike on any given pitch?

 To find the probability that Greg will throw a strike, start by drawing a tree diagram that shows the probability that he will throw a fastball or a knuckleball.

The probability of Greg throwing a fastball is 0.7 and the probability of him throwing a knuckleball is 0.3. Notice that the sum of the probabilities of the outcomes is 1 because 0.7 + 0.3 is 1.00.

 Next, add branches for each pitch to show the probability for each pitch being a strike, starting with the fastball:

Remember that the probability of Greg throwing a fastball for a strike is 0.6, so the probability of him not throwing it for a strike is 0.4 (since 0.6 + 0.4 = 1.00)

Repeat this process for the knuckleball:

Remember that the probability of Greg throwing a knuckleball for a strike is 0.2, so the probability of him not throwing it for a strike is 0.8 (since 0.2 + 0.8 = 1.00)

Now that the probability tree diagram has been completed, you can perform your outcome calculations. Remember that the sum of the probability outcomes has to equal one:

Since you are trying to figure out the probability that Greg will throw a strike on any given pitch, you have to focus on the outcomes that result in him throwing a strike: fastball for a strike or knuckleball for a strike:

The last step is to add the strike outcome probabilities together:

0.42 + 0.06 = 0.48

 The probability of Greg throwing a strike is 0.48 or 48%.

Probability Tree Diagrams: Key Takeaways

·      A probability tree diagram is a handy visual tool that you can use to calculate probabilities for both dependent and independent events.

·      To calculate probability outcomes, multiply the probability values of the connected branches.

·      To calculate the probability of multiple outcomes, add the probabilities together.

·      The probability of all possible outcomes should always equal one. If you get any other value, go back and check for mistakes.

---

Keep Learning!

Check out the animated video lessons below to learn more about tree diagrams and probability.

Check out the video lessons below to learn more about how to use tree diagrams and calculating probability in math:

---

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your input in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

10 Fun Math Riddles for Adults (with Answers)

10 Fun (and Free) Math Riddles for Adults

A Post By: Anthony Persico

Who says that having fun solving math problems and puzzles is only for children? 

There are over one hundred thousand web searches for math riddles for adults every month, according to Google. If you are one of these individuals searching for fun, engaging, and sometimes brain-bending math riddles and brain teasers made specifically for adults, then grab a pen and paper and get ready for a challenge!

Working on math riddles as an adult is a great way to keep your mathematical reasoning and problem-solving skills sharp while having a lot of fun at the same time. Today’s post shares 10 super fun math riddles for ages 18+ that were created to challenge the adult mind and they are appropriate for individuals ages 16 and up.

Each math riddle is a unique opportunity to apply your problem-solving skills, mathematical thinking, arithmetic, reasoning, and logic. It is recommended that have a pen, paper, and a calculator on-hand when attempting to solve any of these riddles, as drawing a diagram and working out the math by hand can be extremely helpful.

Helpful Advice Before You Begin…

Before you start working on solving all 10 riddles, here are a few helpful hints for overcoming the inevitable moments when you get stuck and/or are considering giving up on trying to solve the problem:

•  Read each math riddle carefully and think about the problem for a while before doing anything.

• Utilize strategies such as visualizing, drawing diagrams, and trial-and-error when you don’t know where to start.

• Don’t get discouraged! When you are struggling and making mistakes, you are in the process of learning. This is called having a growth mindset!

• Whenever you find a solution, ask yourself “does my answer make sense?”

• If you are stuck on a problem, take a short break, and do something else like taking a short walk. You’ll be surprised by how the problem will become more manageable when you return.

Practice Problem: Captain Anne’s Coins

In case you are feeling a bit rusty and need a quick refresher on how to go about solving math riddles, below is a bonus practice problem that is worked out step-by-step. You can choose to skip this practice problem if you would like.

View fullsize

Here is the problem:

Captain Anne has a chest full of coins.

When she arranges the coins in groups of two, there is one single coin left over. When she arranges the coins in groups of three, five, or six, there is also just one single coin left over. But when she arranges the coins in groups of seven, there are no coins left over.

What is the fewest amount of coins she could have?

 How to solve:

This is a very challenging problem to solve mentally, so using a pen and paper will be a big help (if you are a hands-on learner, you can use real coins to support your thinking and model how to solve this riddle).

In this case, let’s go ahead and create a chart that models all of the possible scenarios, starting with the fact that when she arranges the coins in groups of two, there is one single coin left over. Let’s assume that this is the only true statement that we know, then we could conclude that her total number of coins must be one more than a number that is divisible by two. The possibilities would include:

Possible Coin Totals for Groups of 2: 3, 5, 7, 9, 11, 13, 15, 17, …

You can then go ahead and repeat this process for the statement when she arranges the coins in groups of three, five, or six, there is also just one single coin left over.

Possible Coin Totals for Groups of 3: 4, 7, 10, 13, 16, 19,…

Possible Coin Totals for Groups of 5: 6, 11, 16, 21, 26, 31,…

Possible Coin Totals for Groups of 6: 7, 13, 19, 25, 31, 37,…

Finally, make a list of possibilities for the last statement: but when she arranges the coins in groups of seven, there are no coins left over.

Possible Coin Totals for Groups of 7: 7, 14, 21, 28, 35, 42,…

Now that you have a list of coin total possibilities for each statement, you have to the identify the lowest number that is present on every list. A coin total of 7 is a solid contender because it shows up on almost every list…except for the groups of 5, so the answer must be a different number.

At this point, you’ll notice that there isn’t a number that appears on every list, so you’ll have to start extending them as follows until you find the answer:

View fullsize

Notice that the smallest number that appears on every list is 91.

Final Answer: The fewest number of coins that Captain Anne could have is 91.

Now that you have an idea of how to solve these kinds of math brain teasers, you can try to solve them all! There is a complete answer key at the bottom of this post!

---

10 Fun Math Riddles for Adults

Each of the following math riddles includes an image graphic. Click on any image graphic to enlarge. A complete answer key is included at the bottom of the post.

1.) Math Riddle One of Ten: How Many Handshakes?

If there are 20 people in a room and they each shake each other’s hand once and only once, how many handshakes were there all together?

View fullsize

---

2.) Math Riddle Two of Ten: The Fruit Factor

Each of the fruits in the diagrams below are equal to one of the following whole numbers: 1, 2, 3, or 5. Find the value of each fruit so that both of the equations would be true.

View fullsize

---

3.) Math Riddle Three of Ten: Water Jug Dilemma

You are given an 8-gallon jug filled with water, and also two empty jugs: one that holds 5 gallons and another that holds 3 gallons. Using these three jugs, how can you measure exactly 4 gallons of water?

(This riddle was famously presented to (and successfully solved by) Bruce Willis and Samuel L. Jackson’s characters in Die Hard with a Vengeance.)

View fullsize

---

4.) Math Riddle Four of Ten: The Combo Platter

Oliver orders the combo platter for lunch every Wednesday.

One day, he noticed that the amount he paid for his sushi platter was a rearrangement of the digits of the amount of money he had in his pocket.

He also noticed that the money he had left-over after paying was also a rearrangement of the same three digits.

How much money did Oliver start with?

---

5.) Math Riddle Five of Ten: Amazing Eights

If you had to write down all of the whole numbers between 1 and 100, how many times would you have to write the number 8?

View fullsize

---

Are you looking for more super fun Math Riddles, Puzzles, and Brain Teasers?

The best-selling workbook 101 Math Riddles, Puzzles, and Brain Teasers for Ages 10+! is now available as a PDF download. You can get yours today by clicking here.

---

6.) Math Riddle Six of Ten: Missing Cards

A few playing cards are missing from a standard 52-card deck. Three cards remain when you deal the entire deck to four people. And two cards remain when you deal the entire deck to three people OR if you deal the entire deck to five people. How many cards are missing from the deck?

View fullsize

---

7.) Math Riddle Seven of Ten: Movin’ Matchsticks

How can you make the equation below true by moving only ONE matchstick?

(*Bonus points if you can find three possible solutions!)

Check out this video tutorial on how to solve the famous matchstick problem.

---

8.) Math Riddle Eight of Ten: Extra Eggs

Jenny has ten chickens that lay eggs every day. She wants to give away her extra eggs to her neighbors, but she wants to give each neighbor an equal number of eggs. She figures out that she needs to give 7 of her neighbors eggs for them to get the same amount, otherwise there is one egg left over.

What is the smallest number of eggs she needs for this situation to be true?

---

9.) Math Riddle Nine of Ten: The Fruit Man

Mr. Baccigalupi sells and delivers crates of fruit from his grocery store to the people in his neighborhood. He can either put 8 large pieces of fruit or 10 small pieces of fruit into a crate. In one shipment, he sent a total of 96 pieces of fruit. If the number of large pieces of fruit is greater than the number of small pieces of fruit, how many crates of fruit did he deliver?

View fullsize

---

10.) Math Riddle Ten of Ten: The Juiced Baseball

You have 7 baseballs that all weigh the same except for one, which is lighter than the others. Using a balance scale, how can you figure out which baseball is the lighter one if you only get two chances to weigh them?

View fullsize

---

11.) Bonus Math Riddle! : My Three Daughters

A saleswoman knocks on an apartment door and a man answers. They have the following conversation:

Saleswoman: Hello sir, how many children do you have and what are their ages?

Man: I have three daughters and I will give you a hint to help you figure out how old they are: if you multiply my 3 daughters’ ages, you will get 36.

Saleswoman: That is not enough information!

Man: Well, if you add up my daughters’ ages, the sum is the number of my next-door neighbor’s apartment.

Saleswoman (after looking at the number on the front door of the next apartment): That is still not enough information!

Man: The last hint that I will give you is that my oldest daughter has green eyes.

What are the ages of the man’s three daughters?

---

ANSWER KEY:

1. 190 handshakes (19+18+17+16+...+3+2+1=190)

2. Melon=5, Apple=2, Grapes=3, Lemon=1

3. Start by completely filling up the 5-gallon jug with water. Next,

   pour water from the 5-gallon jug into the 3-gallon jug until it is completely full (leaving 2 gallons in the 5-gallon jug). Then, pour all of the water from the 3-gallon jug back into the 8-gallon jug. Next,

   pour the two gallons of water in the 5-gallon jug into the 3-gallon jug,

   which would leave it with exactly one gallon of available space. Then,

   completely fill the 5-gallon jug a second time. Finally, pour water

   from the 5-gallon jug into the 3-gallon jug until it is completely full

   (thus filling up the one gallon of available space in the 3-gallon jug),

   which leaves you with exactly four gallons of water in the 5-gallon

   jug! (Here is a video explanation that you may find helpful.)

4. Oliver started with $9.54. The value of the money can be written using three digits, so it has to be between $1.01 and $9.99. There is only one set of numbers that works:$4.59 + $4.59 = $9.54

5. 20 Times

6. 5 cards are missing

7. 8-4=4, 5+4=9, 0+4=4 (Here is a great video explanation)

8. The number of eggs must be one more than a number that is divisible by 2, 3, 4, 5, and 6 since each of these numbers leaves a remainder of 1. Therefore, the total is 301 eggs.

9. 11 Crates Total:
   7 filled with large fruit (7 x 8 = 56 pieces of fruit)
   4 filled with small fruit (4 x 10 = 40 pieces of fruit) So there are 11 total crates and 96 pieces of fruit.

10. Start by putting three baseballs on each side. If the scales are even, then the baseball ball that was excluded is the lighter one. But if they aren’t even, one side will weigh down while the other side rises up (this is the lighter side). In this case, one of the three baseballs on the lighter side is the light baseball. You can then take these three baseballs and put one on each side of the scale. If the sides are even, then the excluded baseball is the lighter one. And if they aren’t even, then the one that is lighter is the baseball that you are looking for.

11. (BONUS!) 2, 2, and 9 - Start by finding all of the groups of three numbers that multiply to 36 and write down their sums:

Since 13 is the only sum that repeats and because the salesman says that knowing the apartment number is not enough information, you can narrow it down to two trios: (6 6 1) and (2 2 9). And since the man says that his oldest daughter has green eyes, you know that he only one oldest daughter, so you can rule out (6 6 1).

Click here to sign up for our math education mailing list to start getting free K-12 math activities, puzzles, and lesson plans in your inbox every week!

---

Do YOU Want More Fun Math Riddles, Puzzles, and Brain Teasers?

Check out our math riddle videos on YouTube!

---

Did I miss your favorite math riddles or brain teasers? Share your thoughts, questions, and suggestions in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math and an advisor to Amazon Education's 'With Math I Can' Campaign. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

You Might Also Like…

View fullsize

View fullsize

Celebrate Science Fiction Day With These Free Math Riddles

Science Fiction Day has officially arrived and it is the perfect opportunity to inject some sci-fun into your upcoming math lesson plans. So, if your students love science fiction—from alien attacks to zombie invasions—then they’ll love today’s free Science Fiction Math Riddles and Brain Teasers for Grades 1-8

These kinds of activities are perfect for mixing up your instructions, giving your students opportunities to think creatively about math, and adding some fun learning experiences into your lesson plans.

All of the math riddles, puzzles, and brain teasers below are from sci-fi versions of activities from our best-selling 101 Math Riddles, Puzzles, and Kids Ages 10+!

---

1.) Alien Invasion! (For Grades 1-4)

Answer: There are three yellow slugs, two green teens, and one aquatic cyclops.

---

2.) Zombies! (For Grades 4-8+)

Answer: Day #5 15 Zombies, Day #11 66 Zombies

(Pattern: The number of additional zombies increases by one more than the increase between the previous two cases; +2,+3,+4,+5,+6,...)

---

3.) Bonus! Moon Math (Grades 4-8+)

Answer:  ? = 8 (Relationship: the diagonal values are cubes and cube roots)

---

All of today’s math riddles and brain teasers are holiday versions of the puzzles shared in our best-selling workbook: 101 Math Riddles, Puzzles, and Kids Ages 10+!

Here are some samples from the book:

Guaca-Math

The Gummy Bear Pyramid

In Between

Friday the 13th

101 Math Riddles, Puzzles, and Brain Teasers for Kids Ages 10+! is now available as a PDF download. You can get yours today by clicking here.

Click here to get 100 more math riddles, brain teasers, and puzzles for kids!

---

Did I miss your favorite math holiday riddle for kids? Share your thoughts, questions, and suggestions in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math and an advisor to Amazon Education's 'With Math I Can' Campaign. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

You Might Also Like…