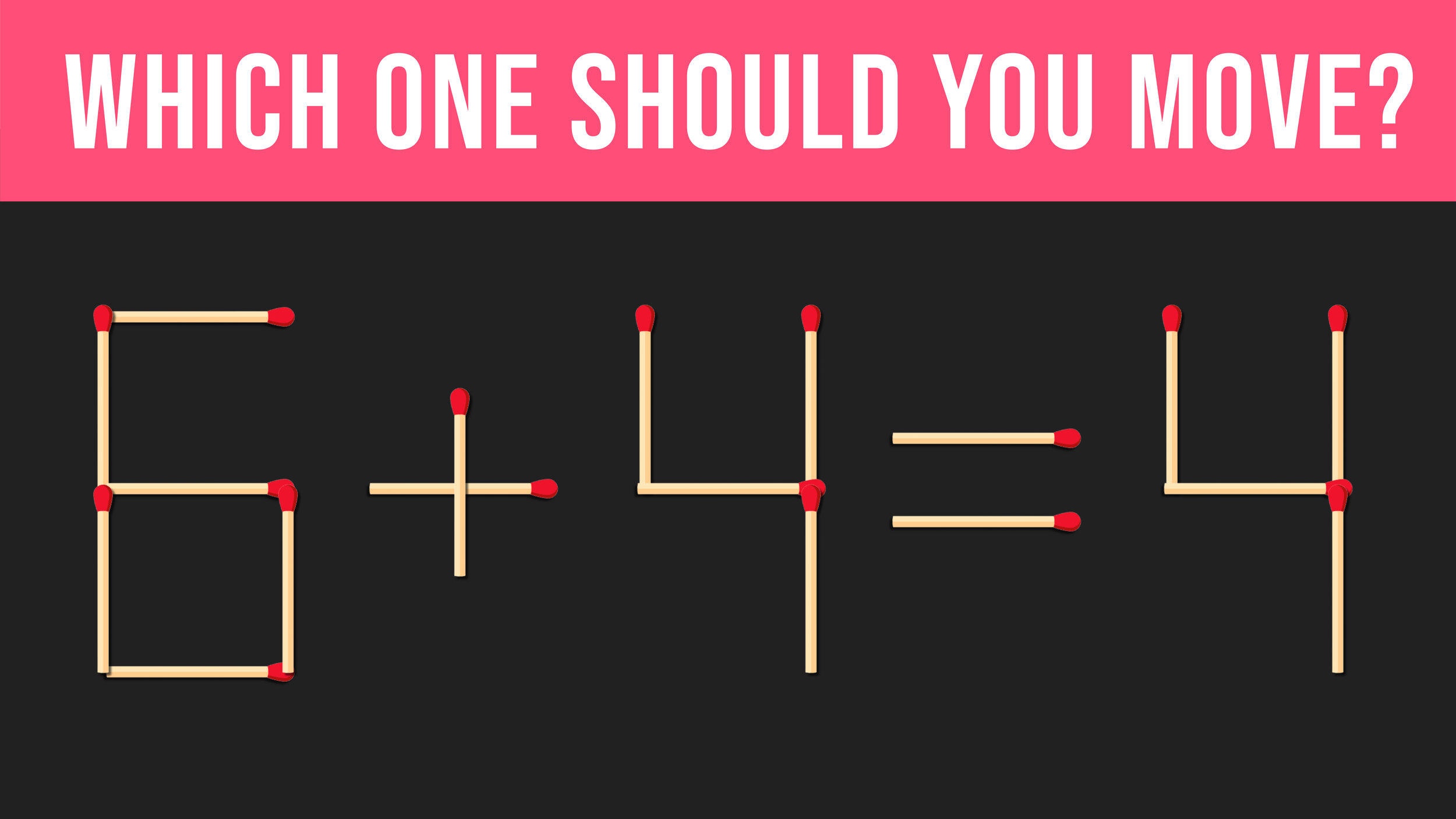Your Kids Will Love These Valentine's Day Math Puzzles

Are you looking for some fun, free, and printable Valentine's Day Math Activities to share with your kids this month?

(We just launched a brand new collection of free Valentine’s Day Math Worksheets for grades K-8! Click here to get your free pdf downloads).

Holiday-themed math puzzles give your kids an opportunity to think critically and deeply about mathematics, develop problem-solving strategies, and work through challenging problems.

And when math problems can channel your students' excitement for Valentine's Day into meaningful learning experiences, engagement will skyrocket!

So, go ahead and try these challenges and puzzles with your kids this month. These free and printable Valentine's Day Math activities are perfect for warm-up and/or cool-down activities and are great for sparking mathematical discussions in your home or classroom. The puzzles are perfect for students in grades 1 through 8.

How to Download: You can download any of the puzzles by right-clicking on the image and saving it to your computer or by dragging-and-dropping it to your desktop.

1.) Find the value of the '?'

Use your math skills to find the value of each icon.

Love = 4

Heart Box = 5

Teddy Bear = 9

Love Birds = 3

? = 7

Hint: 8 minus what value is that same value?

---

2.) Multiplication tables work like a Bingo board, where the value of each box represents the product of its corresponding row and column.

Card = 1

Rose = 2

Heart = 3

Cupid = 6

Chocolates = 18

Looking for more free math challenges like these? click here

---

3.) Which One Doesn't Belong? (simple)

Remember that WODB? activities are meant to spark mathematical thinking and discussion and do not have a single correct answer.

Want to learn more about how to use WOBD? math activities with your kids? click here

---

4.) Multiplication Area Model

Using area model challenge questions is a great strategy for getting kids to think visually about multiplication, which is the approach that Mathematical Mindsets author Jo Boaler recommends most for improving math understanding.

Hint: The area model represents the product of 13 and 9.

Heart = 10

Love Potion = 5

Teddy Bear = 15

Cupid = 12

---

Are you looking for more Valentine’s Day Math Worksheets for students in grades K-8?

Check out our brand new Valentine’s Day Math Worksheet Library to download free holiday-themed pdf worksheets with answer keys.

Click here to get your free pdf worksheets

---

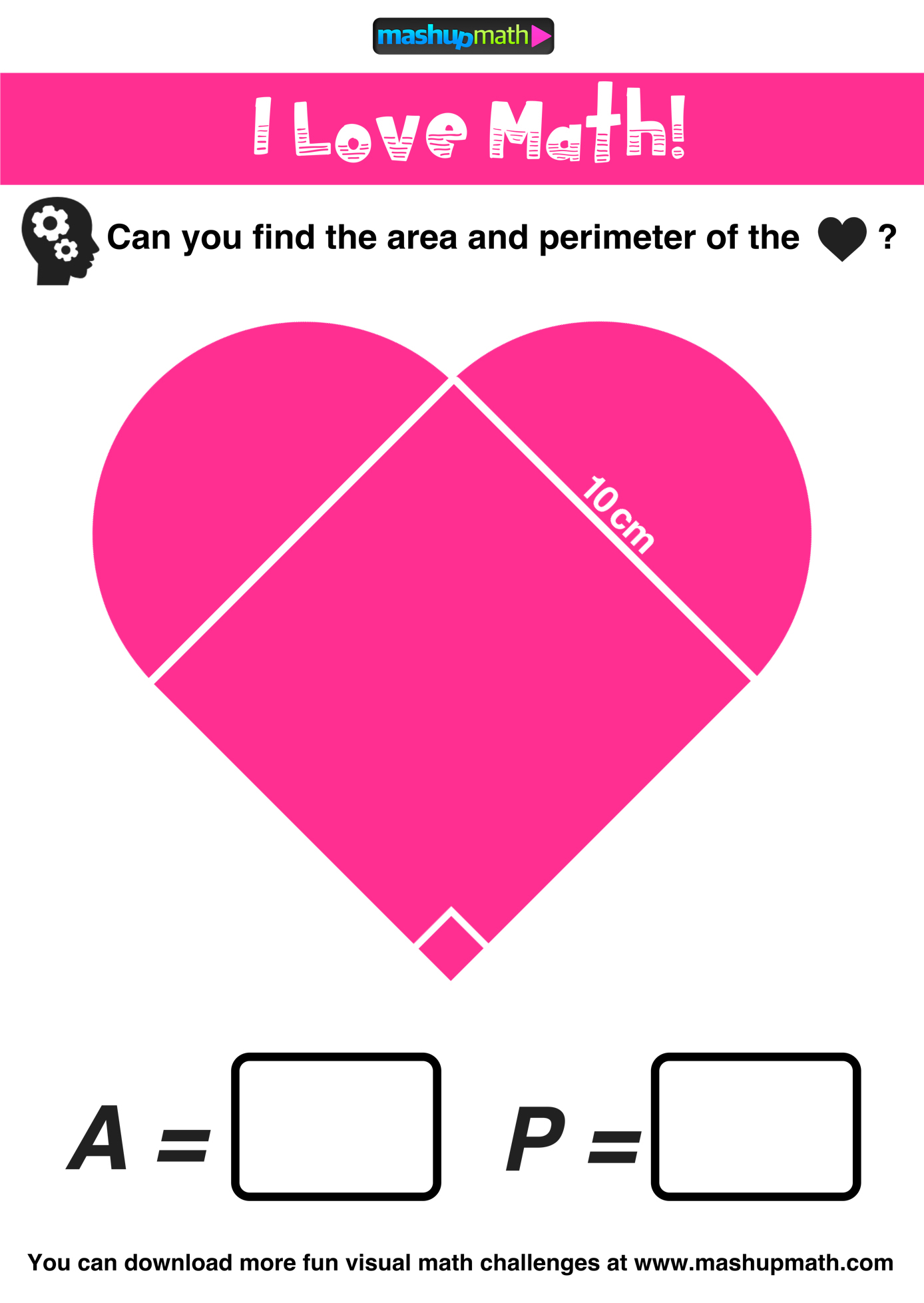
5.) Bonus Geometry Puzzle

Can your kids use their knowledge of area, perimeter, and composite figures to solve this puzzle?

Hint: Two half-circles make one full circle.

Area: approximately 178.5 square cm

Perimeter: approximately 51.4 cm

Do you want to get free math puzzles like this in your inbox every week? Click here to sign up for our free mailing list (includes a free eBook!).

How will you use these math puzzles with your kids? Share your thoughts and suggestions in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math and an advisor to Amazon Education's 'With Math I Can' Campaign. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Can You Solve This Famous Math Riddle? (for Ages 10+)

Most People Can’t Figure Out This Simple Math Riddle. Can You?

The Bridge of Destiny Math Riddle is a twist on the famous bridge and torch problem. This math riddle is seemingly simple and a fan favorite for ages 10 and up, yet many people can’t seem to get the correct answer.

If you love math riddles, brain challenges, and epic quests, then give this one a try and see if you have what it takes to find the answer!

Bridge of Destiny Math Riddle:

• Four travelers on a quest must cross a fragile bridge to continue their journey.

•  No individuals can cross the bridge without the Destiny Gem close by, which, fortunately, they have in their possession.

•  If at any time, more than two individuals walk on the bridge, it will collapse.

•  Each traveler moves at a different pace, and it will take each traveler the following amount of time to cross the bridge:

• Sorceress: 1 minute, Archer: 2 minutes, Warrior: 5 minutes, Wizard: 8 minutes

• When two travelers cross the bridge together, they must move at the slower person's pace.

  What is the shortest time needed for all four travelers to safely cross the bridge?

View fullsize

Remember…

•  No more than two individuals can cross the bridge at the same time (otherwise, it will collapse)

•  Individuals must stay together when crossing the bridge and be in possession of the Destiny Gem

•  All four travelers must get safely across

•  No tricks spells, or throwing the Destiny Gem allowed!

---

Ready to Give This Math Riddle a Try?

Chart Example

Go ahead and try and solve the Destiny Bridge Math Riddle on your own before scrolling any further. Come back when you’re ready to see the answer.

(Hint: Using a chart can be very helpful!)

---

Bridge Riddle Answer

View fullsize

Click to enlarge.

Many people conclude that the shortest amount of time for all four travelers to cross the bridge is 17 minutes, but this is incorrect!

***The actual answer is 15 minutes.

To find the correct answer to the riddle, you must realize that having the two slowest individuals cross the bridge individually wastes valuable time which can be saved if they both cross together.

Detailed Explanation:

Check out our animated Destiny Bridge Riddle Video for a detailed explanation of why the answer is 15 minutes AND for a super fun bonus riddle!

---

Ready for a Bonus Riddle?

Wait! Our travelers need your help yet again. Can you solve the bonus riddle?

The River and The Torch

•  Further along their journey, the four travelers must cross a river at night.

•  Crossing the river after dark is only possible with a torch, so the travelers have traded the Destiny Gem for a Torch that will provide light for 17 minutes after it is lit.

•  Only two travelers can cross the river at one time, and they must have the torch in their possession in order to see where they are going.

•  Each traveler takes the following amount of time to cross the river

•  Wizard: 10 Minutes, Sorceress: 5 Minutes, Archer: 2 Minutes, Warrior: 1 Minute

 How can all four travelers cross the river before the torch burns out?

---

Go ahead and try and solve the River and Torch Math Riddle on your own before scrolling any further. Come back when you’re ready to see the answer.

We'll be here waiting for you when you’re done :)

(Hint: Again, using a chart can be very helpful!)

---

View fullsize

River Riddle Answer

***The answer is 17 minutes.

Just like the bridge riddle, to find the correct answer, you have to save time by having the two slowest individuals (in this case, the wizard and the sorceress) cross the bridge together.

Did you get the correct answer?

---

Looking for a pdf worksheet version of the Destiny Bridge riddle?

Click the link below to get your download (answer key included)

Free Destiny Bridge Riddle PDF Worksheet

---

Today’s math riddle is a sample from our best-selling workbook: 101 Math Riddles, Puzzles, and Kids Ages 10+!

Here are some samples from the book:

Guaca-Math

The Gummy Bear Pyramid

In Between

Friday the 13th

101 Math Riddles, Puzzles, and Brain Teasers for Kids Ages 10+! is now available as a PDF download. You can get yours today by clicking here.

Click here to get 100 more math riddles, brain teasers, and puzzles for kids!

---

More Fun Math Riddles and Brain Teasers You Will Love:

Solving Systems of Equations Explained!

This free step-by-step guide will teach you everything you need to know about solving systems of equations in math.

Solving Systems of Equations: Everything You Need to Know

Solving systems of equations can seem intimidating, especially when you see more than one equation shown on a graph. However, if you know how to graph a function on the coordinate plane or on a graphing calculator, then you can become a master of solving systems of equations.

This guide also includes a very handy system of equations solver that you can use to check your work and graph linear systems on your computer.

But first…

If you need some refreshers on the foundational skills required to understand how to solve systems of equations, you may find these free algebra resources to be helpful:

• Intro to Slope and y=mx+b form (video)

• How to graph a line in slope-intercept form (video)

• Quick Guide to Slope: Parallel and Perpendicular Lines

You’ll also notice that the graphics in this lesson rely on using different colors to differentiate between different functions (this strategy is very helpful for keeping your thoughts organized and preventing confusion). If you are following along using graph paper, then it is highly recommended that you use colored highlighters or markers. However, this is only a suggestion, and you can still learn to solve systems of equations using a pen or pencil.

 Are you ready to get started?

System of Equations Definition

A system of equations is when there are two or more equations that share the same variables.

 For example, here is a system of equations for two linear functions:

y = x + 1 & y=-2x + 1

 Notice that both of these equations are shown on the graph in Figure 1. 

(Again, if you need a refresher on how to graph lines in y=mx+b form, watch this quick video tutorial)

Figure 1 (graph courtesy of desmos.com/calculator)

The solution to a system of equations is the point (or points) where the lines intersect.

 So, in this example, the solution to the system of equations is the point (0,1), since this is where the two lines intersect. 

Figure 2: What do lightsaber fights and linear systems have in common? (Image: Mashup Math MJ)

Types of Solutions to Systems of Equations

Does every system of equations have a solution?

There are actually three kinds of solutions to a system of equations:

• One Solution (as seen in Figure 1)

• No Solution

• Infinitely Many Solutions

Figure 3

Key Takeaways:

One Solution: The systems intersect at only one point.

No Solution: The lines are parallel and do (and never will) intersect

Infinitely Many Solutions: Two or more identical and overlapping graphs that intersect everywhere!

Confused? That’s ok. Just keep the three solution types in mind as we work through an example of each type of solution that will help you to better understand how to solve systems of linear equations.

Systems of Linear Equations Examples

Example 01: One Solution

Find the solution to the following system of equations:

The first step to finding the solution to this system of equations is to graph both lines as follows:

Notice that the ONLY intersection point for this system of equations is at (2,5).

Remember that (2,5) is an (x,y) coordinate where x=2 and y=5. To confirm that you answer is correct, you can substitute x=2 and y=5 into both equations to see if your answer checks out as follows.

Note that, since this system of equations has only one solution, (2,5) is the only point that will work. You can try substituting x and y values for any other coordinate and you will never find another one that works out.

Final Answer: The solution is (2,5)

---

Example 02: No Solution

Find the solution to the following system of equations:

Just like the last example, graph both equations on the coordinate plane as follows:

Notice that both equations have the same slope (+5/4). Since parallel lines have the same slope, it makes sense that the lines are the graph are parallel to each other. And, since parallel lines never intersect, these two lines will never intersect, and therefore there is no solution to this system of equations.

Final Answer: No Solution (because the lines are parallel)

---

Example 03: Infinitely Many Solutions

Find the solution to the following system of equations:

Notice that the second equation is not in y=mx+b form, so you will have to rearrange it to isolate the y before you can graph:

Isolate the y by subtracting 3 from both sides.

What do you notice?

Now we have two equations in our system: y=-4x-3 and… y=-4x-3. After rearranging the second equation, we can see that both equations are identical.

What does this mean for the graph and the solution to our linear system? Let’s find out by graphing the first equation (Figure 5) and then the second equation (Figure 6)

Figure 5

Figure 6

Since the equations are identical, the lines are graphed right on top of each other and they intersect everywhere at every point that both lines pass through.

Therefore, every point on the line is a solution—and since lines have an infinite number of points, this system has an infinite number of solutions.

Final Answer: Infinitely Many Solutions

---

Systems of Equations Solver

When you initially learn how to solve systems of equations, we recommend using graph paper and a straight-edge to graph your equations and find your solution (and use substitution to check your work as we did in example 01).

However, after you become more comfortable working with systems of equations, you may benefit from using systems of equations solver tool like a graphing calculator to graph lines and find intersection points rapidly.

If you don’t have a graphing calculator, there is an awesome FREE system of equations solver calculator available via www.desmos.com/calculator.

*Note that you have to input the equations in y= form in order for the Desmos systems of equations solver to work.

For example, you can use the Desmos Systems of Equations Solver to find the solution to the system:

y=(3/5)x-8 & y=(-8/5)x+3

1.) Type each equation into the left-hand column

2.) Locate the intersection point (you may need to zoom out)

3.) Click on the intersection point to find the coordinates.

The solution is (5,-5)

Screenshot of Desmos.com/calculator

---

Systems of Equations Video Lesson

If you are a visual learner and would like to review this step-by-step guide to solving systems of equations as a video tutorial, check out these free tutorials:

---

---

Keep Learning with These Free Math Guides:

---

Share your ideas, questions, and comments below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

cm to m: 2 Easy Steps

Converting CM to M: Everything You Need to Know

Are you looking to learn how to convert centimeters to meters (cm to m)?

Before you learn the absolute easiest way to convert cm into m (with and without a calculator), let’s do a quick review of some very important vocabulary terms (trust me, this will come in handy very soon):

• Centimeter (cm) is a metric unit of length that equals one-hundredth of a meter.

•  Meter (m) is the fundamental unit of length in the metric system. Note that a meter is approximately 39.37 inches or 3 feet and 3 inches in the imperial system)

• Note that the abbreviations for centimeters (cm) and meters (m) are meant to be expressed as lower-case letters.

The key takeaway from these definitions is that a meter is the standard unit of length in the metric system and that a centimeter is equal to one-hundredth of one meter (which means that there are one hundred centimeters in one meter). Centimeters are very small compared to meters, and:

• One hundred centimeters make up one meter.

• One meter is made up of one hundred centimeters.

Are you starting to see a relationship between centimeters and meters?

Figure 1: Centimeters Compared to Inches (image via Mashup Math FP)

• Remember that meters and centimeters are metric system units of measurement (not imperial).

• For reference, some things that measure approximately 1 meter are the width of a large refrigerator, the depth of the shallow end of a swimming pool, and the height of a typical kitchen countertop.

Figure 2: cm to m Relationship (image via Mashup Math FP)

If you can understand the relationship between cm and m (and m and cm) displayed in Figure 2, then you will be able to convert cm into m using the easy two-step method shown below!

Converting cm to m Examples

You can convert centimeters to meters by following these two easy steps.

(Note: First, you will learn how to convert cm into m by hand and then later on using a calculator).

cm to m Example 01: Convert 500 cm to meters

Let’s start with a relatively simple example, where you have to convert 500 centimeters into meters.

Step One: Divide the Number of Centimeters by 100, as follows:

500 ÷ 100 = 5

Step Two: Change the Units to Meters

500 cm = 5 m

That’s it! (see Figure 3 for a more detailed explanation)

Final Answer: 500 centimeters equals 5 meters

Figure 3

By following the two simple steps above, you can always convert cm to m even if you don’t have a calculator. Now, let’s take a look at another example.

Here is another example of how to convert cm to m:

cm to m Example 02: Convert 886 centimeters into meters

In this example, you can convert cm to m using the same two-step method used in the previous example:

Step One: Divide the Number of Centimeters by 100, as follows:

886 ÷ 100 = 8.86

Step Two: Change the Units to Meters

886 cm = 8.86 m

Final Answer: 886 centimeters equals 8.86 meters

Figure 4. Notice that the answer to this example is a decimal, which is totally fine.

What if you flip cm to m?

Before you move onto learning about the cm to m calculator and trying some free practice problems, let’s take a super quick look at the relationship between the reverse of cm to m: converting meters into centimeters.

As you may have predicted, the conversions between cm and m are reversible. When going form cm to m, you divide by 100. When going in reverse, from m to cm, you multiply by 100.

Fun Fact: If you start with meters and convert to centimeters and then convert back to meters, or vice versa, you will end up with the same number that you started with (some students like to perform these calculations to check that their work is correct).

Example 03: Convert 8.86 meters into centimeters

Notice that this example is the reverse of Example 02 and you have to convert to m into cm. If the fun fact is true, then the final answer has to be 886 centimeters. Let’s see if it works out:

Step One: Multiply the Number of Meters by 100, as follows:

8.86 x 100 = 886

Step Two: Change the Units to centimeters

886 cm = 8.86 m

Final Answer: 8.86 meters equals 886 centimeters

Pretty cool, right?

Figure 5

cm to m Calculator

Screenshot from calculatorsoup.com

If you need a fast and easy way to convert between different units of measurement, including centimeters to meters (cm to m), then you can take advantage of the many free online centimeters to meters conversion calculators that are available.

This free distance conversion calculator from www.calculatorsoup.com will quickly make conversions from cm into m and vice versa, but it will not show you any of the work or the previously mentioned two-step process. While this cm to m calculator is a handy tool, it will not help you understand the process behind making distance conversions or the relationship between centimeters and meters.

To use the cm to m calculator, simply input the number of centimeters in the Value to Convert box and choose to convert from centimeters to meters. If you do not input the numbers correctly, you will not get a correct cm to m conversion.

---

Converting cm to m Practice Problems

Looking for some extra practice converting cm into m (and m into cm)?

The following centimeters to meters practice problems will give you plenty of opportunities to apply the two-step process to converting cm to m or to use a cm to m calculator to make conversions. There is also an answer key at the bottom of this post.

1.) Convert 1,000 cm to m

2.) Convert 2,100 cm to m

3.) Convert 55 m to cm

4.) Convert 3.75 m to cm

5.) Convert 10,222 cm to m

6.) Convert 0.5 m to cm

7.) Convert 1 Million cm to m

8.) Convert 0.01 m to cm

9.) Convert 774 cm to m

10.) Convert 6 Billion cm to m

And if you are looking for some real-world practice problems involving measurement conversions, including converting cm to m, check out this free measurement conversion video lesson:

---

Answer Key:

1.) 10m

2.) 21 m

3.) 5,500 cm

4.) 375 cm

5.) 102.22 m

6.) 50 cm

7.) 10,000 m

8.) 1 m

9.) 7.74 m

10.) 10 million m

---

More Free Decimals and Fractions Resources:

• How to Convert a Fraction to a Decimal

• Video Lesson: Scientific Notation Explained

• Free PDF Math Worksheets (with Answers)

• Activity: Here’s an Awesome Way to Teach Kids Fractions

Keep Learning:

---

Share your ideas, questions, and comments below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

10 Free Maths Puzzles with Answers!

10 Fun (and Free) Maths Puzzles with Answers

A Post By: Anthony Persico

Are You Ready for These Super Fun (and Slightly Brain-Bending) Maths Puzzles?

Every month, thousands of individuals, young and old, search the internet for maths puzzles with answers. Why? Because working on challenging and engaging maths puzzles is more than just a recreational activity. In fact, studies show that working on maths puzzles has several educational benefits including boosting interest in mathematics, improving problem-solving skills and algebra skills, and cultivating reflective learning abilities.

So, if you’re one of these individuals looking to reap the benefits of working on challenging maths puzzles (while having some serious fun while doing so), then you’re in the right place!

Now that you know the benefits of challenging your mind by trying to solve maths puzzles, you’re just about ready to try and solve today’s collection of super fun maths riddles.

Note that these maths riddles with answers are appropriate for individuals ages 12 and up.

Before you get started, here are a few tips to keep in mind when attempting to solve any of today’s maths puzzles:

• Read every maths puzzle carefully and allow yourself to think for a bit before getting started.

• Use proven strategies like visualizing, diagram drawing, and trial-and-error.

• You’re going to struggle! When you find yourself feeling discourages and/or messing up, that means you are in the process of reaping the benefits of solving maths puzzles and improving your problem-solving skills!

• Whenever you find an answer, ask the question “does this solution make sense?”

• If at any time you get stuck, close the page and take a break. This is a good time to take your mind off of the problem by doing something else like going out for a walk. The puzzle will likely become more manageable when you revisit it later on.

Practice Problem: How Many Squares?

Before you attempt the 10 Maths Puzzles with Answers on your own, you may want to get warmed-up with a relatively easy maths puzzle just to get your brain fired up and ready for some more challenging problems later on.

Of course, you can choose to continue on and skip this practice problem if you’d like.

View fullsize

Here is the problem:

How many SQUARES are in the 3x3 grid?

How to solve:

This is a relatively straightforward maths puzzle to solve, provided that you consider two pieces of information:

• A square is a plane figure with four equal sides and four right angles.

• Some squares are overlapping in the diagram.

Want to try the problem on your own? If so, don’t go any further. Stop here and try to solve the puzzle and come on back when you’re finished.

…

The most common way to solve this problem is to consider all the squares, from smallest to largest, and count them as follows:

View fullsize

Final Answer: 14 Total Squares

Wasn’t that fun? Now you are ready to move onto some more challenging maths puzzles!

---

10 Fun Maths Puzzles with Answers

Each of the following math puzzles with answers includes an image graphic. Click on any image to enlarge. The complete answer key for all 10 maths puzzles is included at the bottom of the page.

Have fun!

1.) Maths Puzzles 01 of 10: How Many Rectangles?

This problem may seem very similar to the practice problem, but the subtle difference between Squares and Rectangles is a very big deal that makes this problem rather tricky. (Click here to learn more about this controversial maths puzzle)

Can you solve it?

View fullsize

(Hint: By definition, is a square a rectangle?)

---

2.) Maths Puzzle 02 of 10: Factors and Fruit

Problem: If each piece of fruit in the diagram below is equal to one of the following numbers: 1, 2, 3, or 5, then what is the value of each fruit so that both equations are true?

View fullsize

---

3.) Maths Puzzle 03 of 10: Moon Math

Problem: What is the value of the missing number “?” in the lunar diagram below?

View fullsize

Hint: Look for a pattern.

---

4.) Maths Puzzle 04 of 10: Which is More Pizza?

Problem: Which deal gets you the most pizza (if each deal costs the same amount):

• One 18” pizza pie, or

• Two 12” pizza pies

Can you solve it?

Use the area of a circle formula: A= π(r^2)

---

5.) Maths Puzzle 05 of 10: Super Maths!

Problem: Find the value of each symbol and the ‘?’ in the puzzles below:

Puzzle 1

View fullsize

Puzzle 2

View fullsize

Puzzle 3

View fullsize

---

Are you looking for more super fun Maths Riddles, Puzzles, and Brain Teasers?

The best-selling workbook 101 Math Riddles, Puzzles, and Brain Teasers for Ages 10+! is now available as a PDF download. You can get yours today by clicking here.

---

6.) Maths Puzzle 06 of 10: How Many Triangles

Problem: What is the total number of triangles in the diagram below?

View fullsize

---

7.) Maths Puzzle 07 of 10: Matchsticks Maths

Problem: Make the maths equation true by moving ONE AND ONLY ONE matchstick?

(*Bonus if you can find all three possible answers)

See Also: video tutorial on solving the matchstick maths problem.

---

8.) Maths Puzzle 08 of 10: How Many Total Handshakes?

Problem: If there are 20 people in a room and they shake every other person’s hand once and only once, how many handshakes would take place?

---

9.) Maths Puzzle 09 of 10: Shopping Spree!

Problem: At the mall, the total cost of a pair of shoes and a hoodie is $150. The cost of the hoodie is $100 more than the cost of the pair of shoes. How much does each item cost?

View fullsize

---

10.) Maths Puzzle 10 of 10: Parking Lot Puzzle

Problem: In the diagram below, what is the number of the parking spot occupied by the car?

View fullsize

---

11.) Bonus Maths Puzzle! : The Big Triple!

View fullsize

---

MATHS PUZZLES ANSWER KEY:

1. 36 Total Rectangles (click here to learn more about how to solve this problem)

2. Melon=5, Apple=2, Grapes=3, Lemon=1

3. ?=8 (the relationship between the diagonals are cubes and cube roots)

4. Area of 18” Pizza: ~254.3 square inches > Area of two 12” pizzas: 226 square inches

   (click here to learn more about how to solve this problem)

5. Puzzle #1: DK=12, Bananas=8, Barrell=4, ?=24

   Puzzle #2: Mario=12, Peach=12, Toad=6, Bowser=0, ?=30

   Puzzle #3: Van=8, Zombie=9, Scooby=5, ?=77

6. 27 Total Triangles

7. 8-4=4, 5+4=9, 0+4=4 (Here is a great video explanation)

8. 190 handshakes (19+18+17+16+...+3+2+1=190)

9. Hoodie costs $125, Shoes cost $25

10. 87 (click here to learn how to solve this problem)

11. (BONUS!) 1+2+3=6 and 1 x 2 x 3 = 6

Click here to sign up for our math education mailing list to start getting free K-12 math activities, puzzles, and lesson plans in your inbox every week!

---

Do YOU Want More Fun Math Riddles, Puzzles, and Brain Teasers?

Check out our math riddle videos on YouTube!

---

Did I miss your favorite math riddle for adults? Share your thoughts, questions, and suggestions in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math and an advisor to Amazon Education's 'With Math I Can' Campaign. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

You Might Also Like…

View fullsize