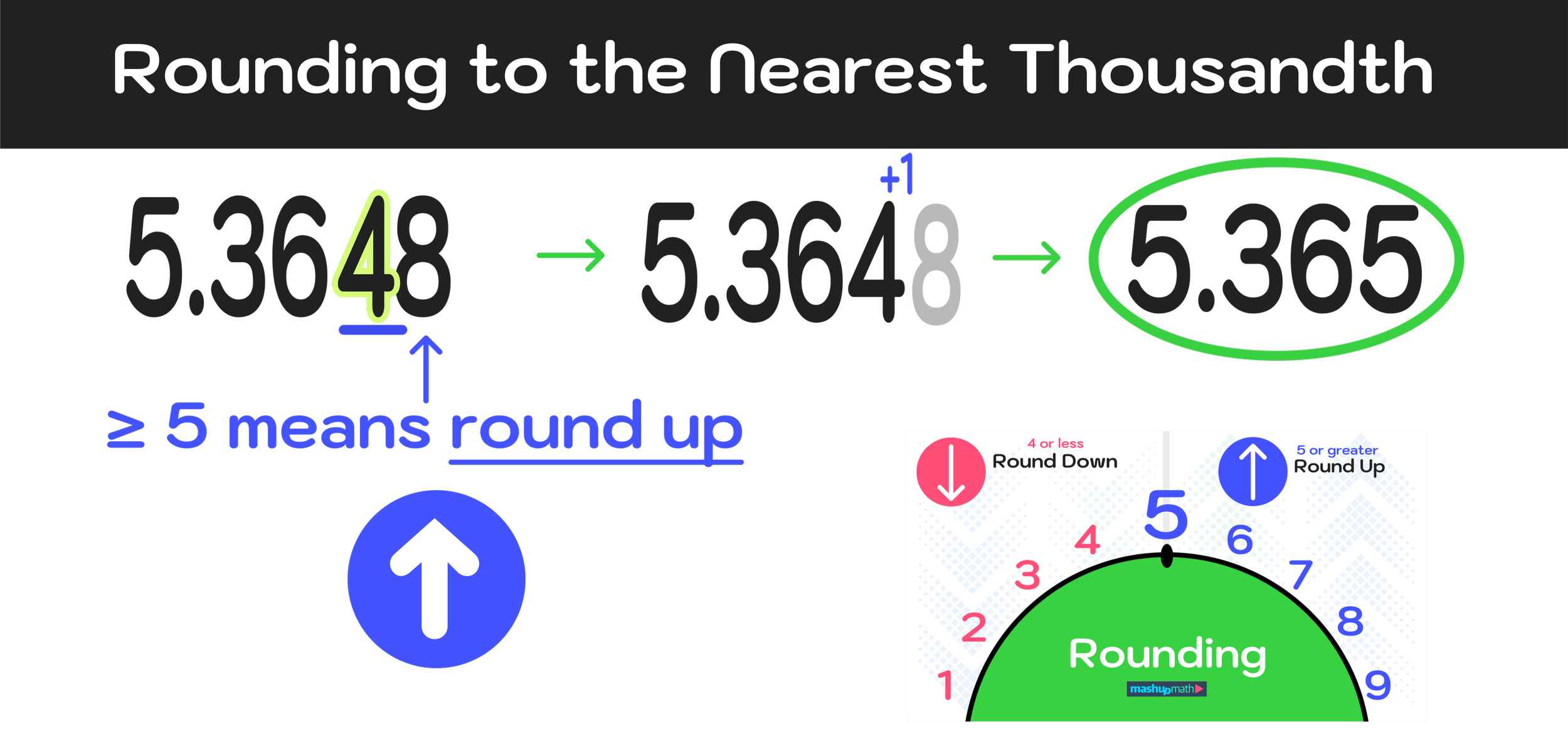
11 Inspiring Growth Mindset Quotes for All Ages

5 Comments

11 Inspiring Growth Mindset Quotes for All Ages

11 Inspiring Growth Mindset Quotes for All Ages

The Best Quotes About Growth Mindset of All Time

Looking for inspirational growth mindset quotes? (Image: Mashup Math MJ)

Are you looking for a collection of the top 11 quotes about growth mindset?

If so, you’re in the right place. This post shares 11 of the most inspiring growth mindset quotes of all time, many of which you will inspire you to take on new challenges and to learn new things.

With a growth mindset for learning you view mistakes as learning opportunities, persevere through challenges, and value personal growth over end results. But nurturing a growth mindset takes time and consuming the right types of messages on a consistent basis is a great strategy for keeping you on the right path.

 
 

One great way to keep yourself motivated along your journey of developing a growth mindset is to have access to inspirational growth mindset quotes from successful individuals whom you admire. These role models can help you to see the power of developing a growth mindset for learning and how long-term success often depends on one’s ability to learn from their mistakes and embrace challenges head-on.

Below you will find 10 of our favorite quotes about growth mindset. This collection of growth mindset quotes features men and women from a variety of backgrounds and careers, so you will surely find a few that will be inspirational and motivational.

11 Inspirational Growth Mindset Quotes

Quotes about Growth Mindset #1: Carol Dweck

The passion for stretching yourself and sticking to it, even (or especially) when it’s not going well, is the hallmark of the growth mindset.

-Carol Dweck

The first entry on our list of growth mindset quotes comes Stanford professor and growth mindset pioneer Carol Dweck. (Image: Mashup Math MJ)

Quotes about Growth Mindset #2: Albert Einstein

It’s not that I’m so smart, it’s just that I stay with problems longer.

-Albert Einstein

The second entry on our list of growth mindset quotes comes from the great Albert Einstein. (Image: Mashup Math MJ)

Quotes about Growth Mindset #3: Oprah Winfrey

I’ve come to believe that each of us has a personal calling that’s as unique as a fingerprint, and that the best way to succeed is to discover what you love and then find a way to offer it to others in the form of service, working hard, and also allowing the energy of the universe to lead you.

-Oprah Winfrey

Our third inspirational growth mindset quote comes from Oprah Winfrey. (Image: Mashup Math MJ)

Quotes about Growth Mindset #4: Michael Jordan

I can accept failure, everyone fails at something. But I can’t accept not trying.

-Michael Jordan

This growth mindset quote from Michael Jordan is one of the best of all time! (Image: Mashup Math MJ)

Quotes about Growth Mindset #5: Steve Jobs

Sometimes when you innovate, you make mistakes. It is best to admit them quickly, and get on with improving your other innovations.

-Steve Jobs

Our next growth mindset quote comes from Apple Cofounder Steve Jobs. (Image: Mashup Math MJ)

Quotes about Growth Mindset #6: Bruce Lee

Persistence, persistence, and persistence. The Power can be created and maintained through daily practice—continuous effort.

-Bruce Lee

Our sixth inspirational growth mindset quote comes from martial artist Bruce Lee. (Image: Mashup Math MJ)

Quotes about Growth Mindset #7: Thomas Edison

Many of life’s failures are people who did not realize how close they were to success when they gave up.

– Thomas Edison

This inspirational growth mindset quote is by inventor Thomas Edison. (Image: Mashup Math MJ)

Looking for inspirational Growth Mindset Quotes to share with your kids?

Access over one hundred printable Growth Mindset quote posters for your classroom in our brand new PDF eBook!

Quotes about Growth Mindset #8: Ariana Grande

Learn from your mistakes. Take responsibility and forgive yourself.

-Ariana Grande

(Image: Mashup Math MJ)

Quotes about Growth Mindset #9: Pele

Success is no accident. It is hard work, perseverance, learning, studying, sacrifice, and most of all, love of what you are doing or learning to do.

–Pele

One of the best quotes about growth mindset comes from the great Pele. (Image: Mashup Math MJ)

Quotes about Growth Mindset #10: Lebron James

You can't be afraid to fail. It's the only way you succeed. You're not gonna' succeed all the time and I know that.

-Lebron James

One of our top growth mindset quotes comes from Lebron James. (Image: Mashup Math MJ)

Quotes about Growth Mindset #11: Mark Twain

 Twenty years from now you will be more disappointed by the things you did not do than by the ones you did. So… sail away from the safe harbor. Explore. Dream. Discover.

– Mark Twain

Our final growth mindset quote comes from famous American author Mark Twain. (Image: Mashup Math MJ)

Conclusion: Growth Mindset Quotes

Now that you have seen all 11 of our favorite inspirational growth mindset quotes, it should be clear that the art of learning from one’s mistakes, practicing persistence, and viewing personal growth as a lifelong journey is both a timeless and ageless pursuit. Each growth mindset quote serves as a strong reminder that your potential for growth has no limitations. As long as you are willing to give effort and not get discouraged by your mistakes, you will be able to learn and to grow.

In your everyday life, you can use these insights to supply you with inspiration and motivation as you take on new challenges and continue to develop your own growth mindset for learning. In doing so, you are making a commitment to becoming ever persistent, resilient, and a true lifelong learner.

If you would like to learn more about a growth mindset for learning and its incredible benefits, check out our in-depth article on Defining a Growth Mindset for Learning (and Why it Matters).

 
 

5 Comments

Is 0 a Whole Number? (Instant Answer)

Is 0 a Whole Number? (Instant Answer)

Is 0 a Whole Number? Yes or No?

What is the definition of a whole number and is 0 a whole number?

 

Is 0 a Whole Number? (Image: Mashup Math MJ)

 

When learning about the different categories of numbers (natural numbers, whole numbers, integers, etc.), zero can sometimes get lost in the shuffle. Many students often wonder: “Is 0 a whole number?” If you are asking this question yourself, you can click here for an instant answer or you can read through this short guide for a complete explanation, which includes definitions to some important math vocabulary terms related to numbers.

Before we determine whether or not 0 is a whole number, let’s do a quick review of the difference between natural numbers and whole number in math.

Natural Numbers

In math, a natural number is a number that can be used for counting or ordering values or amounts. The set of natural numbers starts at 1 and continues as follows: { 1, 2, 3, 4, 5, 6, 7, …}

Notice that 0 is not included in this set and, thus, 0 is not a natural number.

Whole Numbers

In math, a whole number is any number that does not include fractions, decimals, or negatives. Another way to think about the set of whole numbers is a set that includes all of the positive integers as well as zero. The set of whole numbers starts at 0 and continues as follows: { 0, 1, 2, 3, 4, 5, 6, 7, …}

Notice that 0 is indeed included in this set and, thus, we can conclude that…

 

Figure 01: The Universe of Number: Is 0 a Whole Number?

 

Is 0 a Whole Number?

Instant Answer: Zero is a Whole Number

Yes, zero is a whole number.

Why? By definition, 0 is not included in the set of natural numbers (i.e. zero is not a natural number), but it is included in the set of whole numbers (i.e. zero is a whole number).

Additionally, 0 is the first whole number and is followed by 1, 2, 3, 4, 5, etc.

The graphic in Figure 02 below shows how zero is included in the set of whole numbers but not in the set of natural numbers.

 

Figure 02: The Universe of Number: Is 0 a Whole Number?

 

Zero's Important Place in the Number System

Why is zero such an important number when it comes to the universe of numbers? We have already established that, by definition, zero is a whole number. As far as values go, zero is unique because it represents the absence of value or a null quantity (i.e. zero represents nothing, which is why it is neither positive nor negative)

So, why is 0 a whole number? Because the concept of counting whole values relies on 0 to serve as a starting point (i.e. the point where you have nothing). Without this starting point, all non-zero whole numbers would lose their context.

If this explanation is hard to understand, we can think about zero’s role as a whole number from a practical standpoint. For example, if you were measuring the number of days that you visited the gym last year, you would rely on 0 to represent the instance where you never attended at all. Then, the remaining whole numbers could be used to determine how many times you actually attended. And since you can’t visit the gym negative times or a fraction/decimal of a time, the set of whole numbers would be used for this particular scenario.

 

Is 0 a Whole Number? Yes! (Image: Mashup Math FP)

 

More Key Facts About Zero

If you were surprised to find out that 0 is a whole number, then you may also be surprised by some other interesting and fundamental facts about zero.

Here are a few examples of some surprising facts about zero,

Zero is a whole number.

Is 0 a whole number? As previously stated, zero is, by definition, a whole number, meaning that it is included in the set of whole numbers {0, 1, 2, 3, 4, 5, …}

Zero is an integer.

Is 0 an integer? Since the set of integers includes all of the whole numbers and their negative counterparts, we can also say that zero is an integer as well.

Zero is neither negative nor positive.

Is 0 positive or negative? The set of integers includes every non-zero whole number and its negative counterpart as well as zero. This definition is worded this way because zero is the only integer that is neither negative nor positive. Zero is important in this sense because it is the “neutral value” that separates all of the positive numbers from the negative numbers.

Zero is an even number.

Is 0 even or odd? While you can’t divide a number by zero, you can divide zero by a number. By definition, a number is even if it can be divided by 2 without any remainder. Since 0/2 = 0, we can say that, by definition, zero is an even number (and that zero is not an odd number).

 
 

Conclusion: Is 0 a Whole Number?

If you find yourself wondering “Is 0 a Whole Number?”, then it’s important that you understand the mathematical definition of a whole number in the first place.

In math, a whole number is any number that does not include fractions, decimals, or negatives. And, since 0 does not include fractions or decimals and is not negative, we know that 0 is included in the set of whole number {0, 1, 2, 3, 4, 5, 6, 7, …}.

In short, the answer to the question “Is 0 a Whole Number?” is yes! By definition, zero is included in the set of whole numbers and it plays the important role of the absence of value or a null quantity. All of the non-zero whole numbers have a value that is determined based on its distance from zero on the number line. Pretty cool, right?

Additionally, while zero is not a natural number, it is all of the following:

  • zero is a whole number

  • zero is an integer

  • zero is neither positive nor negative

  • zero is an even number

Whether you came to this page looking for a simple yes or no answer or a deep exploration of the properties of 0, we hope that you leave here with a greater appreciation of 0 and its status in the universe of real numbers. As you continue to learn zero’s place in the number system, you will continue to gain a deeper understanding of mathematics and numbers in general.

 
 

More Free Resources You Will Love:

Image: Mashup Math MJ

Why Am I So Bad at Math? (And How to Get Better)

If you are wondering, why am I so bad at math? The fault is likely due to you having a fixed mindset for learning, which is often a product of being negatively affected by harmful misconceptions about your ability to learn math.

How to Multiply Fractions in 3 Easy Steps

Comment

How to Multiply Fractions in 3 Easy Steps

How to Multiply Fractions in 3 Easy Steps

Math Skills: Learn how to multiply fractions by fractions, how to multiply fractions with whole numbers, and how to multiply mixed fractions.

 

Free Step-by-Step Guide: How to Multiply Fractions Explained

 

Once you have learned how to add fractions and how to subtract fractions, you are ready to start multiplying fractions in a variety of scenarios.

This free guide will teach you everything you need to know about how to multiply fractions in the following ways:

The task of having to multiply fractions together may seem challenging at first, but the procedure is actually quite simple and something that you can learn by working through a handful of practice problems, which is exactly what we will be doing in this free step-by-step guide.

While we highly recommend that you work through the guide from start to finish, you can use the quick-links above to jump to a particular topic section.

For all of the problems in this guide, we will be using an easy 3-step strategy that can be used to solve any problem where you have to multiply fractions to get a solution. So, if you can learn how to follow three easy steps, you can correctly answer any multiplying fractions problem!

Are you ready to get started?

Before we start working on the multiplying fractions practice problems, let’s do a quick recap of some key vocabulary terms related to fractions.

How to Multiply Fractions: Vocabulary Recap

This guide uses several math vocabulary terms related to fractions that you will need to be familiar with in order to learn this new math skill. Be sure that you understand the meaning of the following key vocabulary terms before moving forward in this guide.

The Numerator of a Fraction

For any fraction, the numerator is the number at the top of the fraction. For example, the fraction 4/5 has a numerator of 4 since 4 is at the top of the fraction.

The Denominator of a Fraction

For any fraction, the denominator is the number at the bottom of the fraction. For example, the fraction 4/5 has a denominator of 5 since 5 is at the bottom of the fraction.

In this guide, any mention of a numerator is referring to the top number of a fraction and any mention of a denominator is referring to bottom number of a fraction. This relationship between the numerator and the denominator of a fraction is illustrated in Figure 01-A below.

 

Figure 01-A: In any fraction, the numerator is the top number and the denominator is the bottom number.

 

Moving on, let’s recap three more key vocabulary terms and concepts related to fractions:

Whole Numbers

A whole number refers to any number that does not contain any fractions or decimals (i.e. an integer). Some examples of whole numbers include 4, 51, and 263.

Note that any whole number can be expressed in fraction form by rewriting it as a fraction with a denominator of 1. For example, the number 4 can be rewritten as a fraction as 4/1. This fact will come in handy later on when you learn how to multiply a fraction by a whole number.

 

Figure 01-B: How to Rewrite a Whole Number as a Fraction: Rewrite the given whole number as a fraction with a denominator of 1.

 

Proper Fractions

A fraction is a number that represents a part of a whole number. 1/4, 3/5, and 7/8 are all examples of fractions.

Note that proper fractions have a numerator that is smaller than the denominator.

Mixed Fractions (Mixed Numbers)

A mixed fraction (or a mixed number) is any number that represents the sum of a whole number and a proper fraction. For example, 7 5/8 is a mixed number that is equal to the sum of 7 and 5/8.

Note that mixed fractions can also be expressed as improper fractions (fractions whose numerator is greater than its denominator).

 

Figure 02: What is the difference between a whole number, a fraction, and a mixed number.

 

Now that you are familiar with these vocabulary terms, you’re ready to learn how to multiply fractions using our easy 3-step strategy.

How to Multiply Fractions by Fractions

How to Multiply Fractions by Fractions: Example #1

Example #1: 1/2 x 3/4

To solve this first example, where we are tasked with finding the product of 1/2 (one-half) and 3/4 (three-quarters), we will use the following three-step strategy for multiplying fractions:

How to Multiply Fractions in 3 Easy Steps

  • Step One: Multiply the numerators together.

  • Step Two: Multiply the denominators together.

  • Step Three: See if the resulting fraction can be simplified or reduced.

When it comes to multiplying fractions, the process is extremely straightforward, and you can use these three steps to solve any fraction multiplication problem!

So, let’s go ahead and use these three steps to solve this first problem: 1/2 x 3/4 = ?

Step One: Multiply the numerators together.

For this problem, we have two fractions: 1/2 x 3/4

The first step requires us to multiply the two numerators (top numbers) together as follows:

  • 1 x 3 = 3

Step Two: Multiply the denominators together.

The second step requires us to multiply the two denominators (bottom numbers) together as follows:

  • 2 x 4 = 8

Step Three: See if the resulting fraction can be simplified or reduced.

Now we have a new fraction with a numerator of 3 and a denominator of 8:

  • 1/2 x 3/4 = 3/8

For the final step, we have to see if the result can be further simplified or reduced. If it can’t, our result will be our final answer.

In this case, 3/8 can not be simplified or reduced any further and we can conclude that:

Final Answer: 1/2 x 3/4 = 3/8

Figure 03 below illustrates how we solved the first example using the three-step strategy.

 

Figure 03: How to Multiply Fractions: Multiply the numerators together, then multiply the denominators together. Finally, simplify the resulting fraction if possible and you’re done!

 

Note that it’s okay if you are still a little confused. The more experience you gain using this 3-step strategy to multiply fractions, the easier these type of problems will become. Let’s go ahead and work through another example.

How to Multiply Fractions by Fractions: Example #2

Example #2: 5/6 x 4/7

Let’s go ahead and solve Example #2 exactly the same as we did the previous example.

Step One: Multiply the numerators together.

For step one, we have to find the product of the two numerators, 5 and 4:

  • 5 x 4 = 20

Step Two: Multiply the denominators together.

For step two, we have to find the product of the two denominators, 6 and 7:

  • 6 x 7 = 42

Step Three: See if the resulting fraction can be simplified or reduced.

Our result is a fraction with a numerator of 20 and a denominator of 42:

  • 5/6 x 4/7 = 20/42

Can the result, 20/42, be reduced? The answer is yes, because both numbers have a greatest common factor of 2. So, after dividing both the numerator and the denominator by 2, we can conclude that:

Final Answer: 5/6 x 4/7 = 20/42 = 10/21

Figure 04 below illustrates how we determined that 5/6 x 4/7 = 10/21

 

Figure 04: How to Multiply Fractions: Be sure to express your answer in reduced form.

 

Next, let’s go ahead and solve one more practice problem where we’ll have to multiply one fraction by another fraction.

How to Multiply Fractions by Fractions: Example #3

Example #3: 9/16 x 7/12

Again, we can use the same three-step strategy to solve this third example as follows:

Step One: Multiply the numerators together.

In this case, the numerator of the first fraction is 9 and the numerator of the second fraction is 7.

  • 9 x 7 = 63

Step Two: Multiply the denominators together.

In this case, the denominator of the first fraction is 16 and the denominator of the second fraction is 12.

  • 16 x 12 = 192

Step Three: See if the resulting fraction can be simplified or reduced.

Now we have a new fraction with a numerator of 62 and a denominator of 192:

  • 9/16 x 7/12 = 63/192

To see if this result can be reduced, we have to see if 63 and 192 both share a GCF. Since both of these numbers are divisible by 3, we can divide both the numerator and the denominator by 3 to get our final answer in reduced form:

Final Answer: 9/16 x 7/12 = 63/192 = 21/64

The graphic in Figure 05 below shows we successfully multiplied two fractions in this example.

 

Figure 05: How to Multiply Fractions Step-by-Step.

 

Now that you have some experience with multiplying fractions, let’s move onto the next section where you will learn how to multiply a fraction by a whole number and how to multiple a whole number by a fraction.

How to Multiply Fractions with Whole Numbers

The second section of this guide will focus on how to multiply a fraction with by a whole number and how to multiply a whole number by a fraction.

Luckily, the three-step method that we used to solve problems in the previous section will work here as well. If you are unfamiliar with how to multiply a fraction by a fraction, we highly recommend that you go back and work through the above examples.

Now, let’s jump into our first example on how to multiply fractions with whole numbers!

How to Multiply a Fraction by a Whole Number: Example #1

Example #1: 3/8 x 2

When learning how to multiply fractions with whole numbers, it is important to remember that any whole number can be rewritten as an equivalent fraction by rewriting it as a fraction with a denominator of 1.

Since any whole number can be expressed as a fraction in this way, we can solve problems where you have to multiply a fraction by a whole number simply by rewriting the whole number as a fraction and then using the same 3-step strategy from the previous section to solve it.

For this example, we can rewrite the whole number, 2, as 2/1 and rewrite the original problem as:

  • 3/8 x 2 → 3/8 x 2/1

Now, we can find the product by using our three steps:

Step One: Multiply the numerators together.

In this case, the numerator of the first fraction is 3 and the numerator of the second fraction is 2.

  • 3 x 2 = 6

Step Two: Multiply the denominators together.

In this case, the denominator of the first fraction is 8 and the denominator of the second fraction is 1.

  • 8 x 1 = 8

Step Three: See if the resulting fraction can be simplified or reduced.

Finally, we are left with a new fraction with a numerator of 6 and a denominator of 8:

  • 3/8 x 2/1 = 6/8

And, since 6 and 8 are both divisible by 2, we know that the fraction 6/8 can be simplified to:

Final Answer: 3/8 x 2/1 = 6/8 = 3/4

Figure 06 illustrates how we solved this problem.

 

Figure 06: How to Multiply a Fraction by a Whole Number: Rewrite the whole number as a fraction with a denominator of 1.

 

Next, let’s take a look at another example of how to multiply fractions by whole numbers.

How to Multiply a Fraction by a Whole Number: Example #2

Example #2: 5/8 x 6

For this next practice problem, we can rewrite the whole number, 6, as 6/1 and rewrite the original problem as:

  • 5/8 x 6 → 5/8 x 6/1

From here, we can solve this problem as follows:

Step One: Multiply the numerators together.

Start by multiplying the numerators of both fractions together:

  • 5 x 6 = 30

Step Two: Multiply the denominators together.

Next, continue with multiplying the denominators of both fractions together:

  • 8 x 1 = 8

Step Three: See if the resulting fraction can be simplified or reduced.

Here we have a resulting fraction with a numerator of 30 and a denominator of 8:

  • 5/8 x 6/1 = 30/8

Notice that this result is an improper fraction since the numerator, 30, is greater than the denominator, 8. We can reduce this result down to 15/4 and leave it as our final answer or we can convert 15/4 to a mixed number, 3 3/4.

Final Answer: 5/8 x 6/1 = 30/8 = 15/4 or 3 3/4

The graphic in Figure 07 shows how we solved solve this problem by multiplying fractions by whole numbers.

 

Figure 07: How to Multiply a Fraction by a Whole Number Step-by-Step.

 

How to Multiply a Whole Number by a Fraction: Example #3

Example #3: 9 x 2/3

Notice that this third example requires you to multiply a whole number by a fraction (rather than a fraction by whole number like in the last two examples). Since multiplication is associative, the order of the terms won’t change the way that you solve the problem, so we can again use our three-step strategy as follows:

First, just like the previous two examples, rewrite the whole number (9 in this case) as a fraction with a denominator of 1.

  • 9 x 2/3 → 9/1 x 2/3

Step One: Multiply the numerators together.

Multiply the numerators together as follows:

  • 9 x 2 = 18

Step Two: Multiply the denominators together.

Multiply the denominators together as follows:

  • 1 x 3 = 3

Step Three: See if the resulting fraction can be simplified or reduced.

The resulting fraction has a numerator of 18 and a denominator of 3:

  • 9/1 x 2/3 = 18/3

The resulting improper fraction, 18/3, can be simplified. Since both 18 and 3 share a GCF of 3, we can perform 18/3 = 6/1 = 6 and conclude that

Final Answer: 9/1 x 2/3 = 18/3 = 6

All of the steps for solving this example are shown in Figure 08 below.

 

Figure 08 How to Multiply a Whole Number by a Fraction Step-by-Step

 

How to Multiply a Whole Number by a Fraction: Example #4

Example #4: 12 x 7/8

For this next example, we have to rewrite the whole number (12 in this case) as a fraction with a denominator of 1 and then use our three-step strategy to solve:

  • 12 x 7/8 → 12/1 x 7/8

Step One: Multiply the numerators together.

For step one, multiply both of the numerators:

  • 12 x 7 = 84

Step Two: Multiply the denominators together.

For step two, multiply both of the denominators:

  • 1 x 8 = 8

Step Three: See if the resulting fraction can be simplified or reduced.

The result is a new fraction with a numerator of 84 and a denominator of 8:

  • 12/1 x 7/8 = 84/8

Now we have to see if 84/8 can be simplified. Both 84 and 8 share a GCF of 4, so after dividing both numbers by 4, the result is 21/2. While 21/2 can not be simplified further, it is an improper fraction that can be expressed as a mixed number, 10 1/2.

Final Answer: 12/1 x 7/8 = 84/8 = 21/2 or 10 1/2

Figure 09 below illustrates how we were able to multiply a whole number by a fraction to solve this problem.

 

Figure 12: Whenever you end up with an improper fraction, you will likely have to convert it to a mixed number.

 

Now that you know how to multiply a fraction by a whole number and how to multiply a whole number by a fraction, it’s time to move onto the final section where we will go over how to multiply mixed fractions.

How to Multiply Mixed Fractions

How to Multiply Fractions with Mixed Numbers: Example #1

Example #1: 3/5 x 4 1/2

Multiplying fractions with mixed numbers can be done using our same three-step strategy, but with one small extra step at the very beginning.

Before you can solve this problem, you will have to convert the mixed number into an improper fraction.

For this example, the mixed number 4 1/2 can be rewritten as 9/2 (both of these are equivalent):

  • 3/5 x 4 1/2 → 3/5 x 9/2

Now, we can solve 3/5 x 9/2 to find the answer to this problem as follows:

Step One: Multiply the numerators together.

Start off multiplying the numerators of both fractions:

  • 3 x 9 = 27

Step Two: Multiply the denominators together.

Continue by multiplying the denominators of both fractions:

  • 5 x 2 = 10

Step Three: See if the resulting fraction can be simplified or reduced.

After steps one and two, we are left with the improper fraction 27/10.

  • 3/5 x 9/2 = 27/10

While 27/10 can not be simplified, it can be expressed as the mixed number 2 7/10.

Final Answer: 3/5 x 9/2 = 27/10 = 2 7/10

Note that 27/10 is technically a correct answer, but most problems requiring you to multiply mixed fractions will call for you to express your final answer as a mixed fraction.

See Figure 10 for step-by-step details of how we solved this problem.

 

Figure 10: How to Multiply Fractions with Mixed Numbers

 

Moving on, let’s work through one final practice problem where we will have to multiply a mixed number by another mixed number.

How to Multiply Mixed Fractions: Example #2

Example #2: 4 1/5 x 3 2/3

For this example, notice that there are two mixed numbers.

Similar to the previous example, you will have to convert both mixed numbers into equivalent improper fractions before you can use the three-step strategy to solve:

  • 4 1/5 = 21/5

  • 3 2/3 = 11/3

Now we can go ahead and find the answer by solving 21/5 x 11/3

Step One: Multiply the numerators together.

First, find the product of the numerators of both fractions:

  • 21 x 11 = 231

Step Two: Multiply the denominators together.

Next, find the product of the denominators of both fractions:

  • 5 x 3 = 15

Step Three: See if the resulting fraction can be simplified or reduced.

Finally, we are left with the improper fraction 231/15

  • 21/5 x 11/3 = 231/15

While 231/15 is a pretty ugly improper fraction, it can actually be simplified since 231 and 15 share a GCF of 3. So, after dividing both numbers by 3, we are left with 77/5.

  • 21/5 x 11/3 = 231/15 = 77/5

Assuming that we have to express our final answer as a mixed number, we lastly have to rewrite 77/5 as 15 2/5 and we have solved the problem!

Final Answer: 21/5 x 11/3 = 231/15 = 77/5 = 15 2/5

The graphic in Figure 11 below illustrates how we used the 3-step method to solve this problem.

 

Figure 14: How to Multiply Fractions with Mixed Numbers (Step-by-Step)

 

Conclusion: How to Multiply Fractions

Multiplying fractions is an important math skill that you can master with a little bit of practice.

This guide shared a simple and effective 3-step strategy that you can use to solve any problem requiring you to multiply fractions together in any of the following scenarios:

  • multiplying fractions by other fractions

  • multiplying fractions by whole numbers

  • multiplying whole numbers by fractions

  • multiplying mixed fractions

  • multiplying mixed numbers

The good news is that the 3-step strategy shared in this guide can be used to solve problems for all of the above scenarios and can be summarized as follows:

  • Step One: Multiply the numerators together.

  • Step Two: Multiply the denominators together.

  • Step Three: See if the resulting fraction can be simplified or reduced.

The more practice you get using these three steps, the better at multiplying fractions you will become!

Keep Learning

Search Tags: how to subtract fractions, subtracting fractions, how to subtract fractions with different denominators, fraction subtraction, subtracting fractions with unlike denominators, how do you subtract fractions?

Comment

How to Divide Fractions in 3 Easy Steps

1 Comment

How to Divide Fractions in 3 Easy Steps

How to Divide Fractions in 3 Easy Steps

Math Skills: How do you divide fractions by fractions, how do you divide fractions with whole numbers, and how to divide mixed fractions?

 

Free Step-by-Step Guide: How to Divide Fractions Step-by-Step Guide

 

Performing operations on fractions can be challenging. Once you have mastered how to add fractions and how to subtract fractions, the next step is learning how to multiply and how to divide fractions.

The following free guide specifically focuses on teaching you how to divide fractions in the following scenarios:

While dividing fractions may seem challenging at first glance, you can actually easily solve all three types of problems by using a simple 3-step method for dividing fractions, which you will learn and apply to several practice problems further down in this step-by-step guide.

Together, we will learn the Keep-Change-Flip method for how to divide fractions and use it to solve a variety of practice problems.

However, before we dive into working through any examples, let’s do a quick review of some key vocabulary terms and prerequisite skills that you will need to refresh in order to be successful with this new math skill.

Before we cover how to subtract fractions and work through a few examples, let’s do a fast recap of some key characteristics and vocabulary terms related to subtracting fractions.

Are you ready to get started?

How to Divide Fractions: Key Vocabulary

Since we will be using several math vocabulary terms in this guide, it is important that you are familiar with their meanings before you start working on the practice problems.

What is the numerator of a fraction?

The numerator of a fraction is the top number of the fraction. For example, for the fraction 2/3, the numerator is 2.

What is the denominator of a fraction?

The denominator of a fraction is the bottom number of the fraction. For example, for the fraction 2/3, the numerator is 3.

Pretty simple, right? Whenever we mention the numerator of a fraction, we are talking about the top number. On the other hand, whenever we mention the denominator of a fraction, we are talking about the bottom number. Figure 01 below illustrates the relationship.

 

Figure 01: In any fraction, the numerator is the top number and the denominator is the bottom number.

 

Next, let’s make sure that you understand the difference between fractions, whole numbers, and mixed numbers (also referred to as mixed fractions).

What is a whole number?

In math, a whole number is a number that is not a fraction. For example, 7, 23, and 100 are all whole numbers.

What is a fraction?

In math, a fraction is a number that represents a part of a whole number. For example, 1/2, 2/3, and 5/8 are all fractions.

What is a mixed number?

In math, a mixed number (or a mixed fraction) is a number that consists of both a whole number and a proper fraction. For example, 3 2/5 is a mixed number that represents the sum of 3 and 2/5.

Why is it important for you to understand the key characteristics and differences between these three types of numbers? Because, in this guide, you will learn how to work with dividing each type of number using a simple 3-step method.

 

Figure 02: What is a whole number? What is a fraction? What is a mixed fraction?

 

Now that you are familiar with all of the key vocabulary related to how to divide fractions, you are ready to work through some practice problems. Let’s start with learning how to divide fractions by other fractions.

How to Divide Fractions by Fractions

How to Divide Fractions by Fractions: Example #1

Example #1: 1/4 ÷ 1/4

Our first dividing fractions example is very simple, and you may already know the answer. In this case, we are taking the fraction 1/4 (one-fourth) and dividing it by 1/4 (one-fourth). So, we are dividing the same non-zero value by itself, which we should already know will be equal to 1.

Even though we already know what the answer should be, let’s go ahead and learn our 3-step method for dividing fractions to this first practice problem to see if it works as it should.

How to Divide Fractions in 3 Easy Steps

  • Step One: Keep the first fraction as is.

  • Step Two: Change the division sign to a multiplication sign.

  • Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.

We will also be referring to this 3-step method as Keep-Change-Flip. Once you learn how to successfully follow these three simple steps, you can use them to solve any problem where you have to divide fractions!

Let’s go ahead and apply them to this first example: 1/4 ÷ 1/4

Step One: Keep the first fraction as is.

This first thing that you have to do is nothing at all. Simply leave the first fraction as is. So, 1/4 stays as 1/4.

Step Two: Change the division sign to a multiplication sign.

Next, take the division sign (÷) and change it to a multiplication sign (x) as follows:

  • 1/4 ÷ → 1/4 x

Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.

For this last step, take the second fraction and “flip” the position of the numerator and the denominator. So, 1/4 becomes 4/1 as follows:

  • 1/4 → 4/1

Now, we have used the Keep-Change-Flip method transform the original problem:

  • 1/4 ÷ 1/4 → 1/4 x 4/1

Figure 03 below illustrates how we used the keep-change-flip method to transform the original division problem into a multiplication problem.

 

Figure 03: How to Divide Fractions: Transform the original division problem into a multiplication problem using keep-change-flip.

 

Finally, we can solve this problem by multiplying these two fractions together. To do this, simply multiply the numerators together and the denominators together as follows:

  • 1/4 x 4/1 = (1x4) / (4x1) = 4/4 = 1

Final Answer: 1

When we multiply these two fractions together, we are left with (1x4) / (4x1) = 4/4 and we know that 4/4 can be reduced to 1, which we expected the answer to be when we first started this problem!

(Looking for some extra help with multiplying fractions, click here to access our free student guide).

Figure 04 below illustrates how we solved this problem after performing keep-change-flip on the original expression.

 

Figure 04: How to solve Example #1 after performing keep-change-flip on the original problem.

 

Confused? If so, that’s okay. The important thing is that you gain some experience with using keep-change-flip. Now let’s go ahead and apply it to another practice problem.

How to Divide Fractions by Fractions: Example #2

Example #2: 2/3 ÷ 4/5

For this second practice problem, we will again be using the 3-step method:

Step One: Keep the first fraction as is.

The first step, simply keep the first fraction 2/3 the same (i.e. you can just leave it as is).

Step Two: Change the division sign to a multiplication sign.

Next, take the division sign (÷) and change it to a multiplication sign (x) as follows:

  • 2/3 ÷ → 2/3 x

Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.

Finally, flip the positions of the numerator and the denominator of the second fraction as follows:

  • 4/5 → 5/4

Again, these 3-steps can be referred to as keep-change-flip, and they are illustrated below in Figure 05:

 

Figure 05: Transform the original problem from Example #2 using Keep-Change-Flip

 

As you can see, we have transformed the original problem using keep change flip and we can now solve it as follows:

  • 2/3 x 5/4 = (2x5) / (3x4) = 10/12 = 5/6

Final Answer: 5/6

Remember, whenever you are multiplying two fractions together, you have to multiply the numerators together and then multiply the denominators together. In this example, we are left with (2x5)/(3x4) = 10/12, and, since 10 and 12 are both divisible by 2, we can reduce and express our final answer as 5/6.

Figure 06 below shows the complete process for solving this second example.

 

Figure 06: How to Divide Fractions Using the Keep-Change-Flip Method

 

Now, let’s go ahead and work through one more example of dividing a fraction by another fraction.

How to Divide Fractions by Fractions: Example #3

Example #2: 7/8 ÷ 11/12

Step One: Keep the first fraction as is.

As always, start by keeping the first fraction (7/8 in this example) as is.

Step Two: Change the division sign to a multiplication sign.

Next, change the division sign (÷) to a multiplication sign (x):

  • 7/8 ÷ → 7/8 x

Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.

Now, flip the positions of the numerator and the denominator of the second fraction:

  • 11/12 → 12/11

The keep-change-flip process for Example #3 is shown in Figure 07 below:

 

Figure 07: How to transform a fractions division problem using keep-change-flip.

 

Now that have transformed the original problem, we can solve it as follows:

  • 7/8 x 12/11 = (7x12) / (8x11) = 84/88 = 21/22

Final Answer: 21/22

In this case, we end up with (7x12) / (8x11) = 84/88 and, since 84 and 88 are both divisible by 4, we can reduce and express our final answer as 21/22.

Figure 08 illustrates how we solved this problem.

 

Figure 08: How to Divide Fractions Using Keep-Change-Flip.

 

Next, we will learn how to divide fractions with whole numbers.

How to Divide Fractions with Whole Numbers

This next section will teach you how to divide a fraction by a whole number and how to divide a whole number by a fraction. We will again be using the keep-change-flip method to solve these kinds of problems. If you want a more in-depth review of how to use the keep-change-flip method, you can click here to revisit the previous section.

How to Divide a Fraction by a Whole Number: Example #1

Example #1: 3/7 ÷ 2

Ready for some good news? You can use the same keep-change-flip method from the previous section to solve these kinds of problems as well. However, there is one extra step involved. Whenever you want to divide a fraction by a whole number using keep-change-flip, you have to rewrite the whole number as a fraction by giving it a denominator of 1.

For this example, we can rewrite the whole number, 2, as a fraction as follows:

  • 2 → 2/1

These both mean the same thing! Now, we can say that solving the original problem is the same as solving 3/7 ÷ 2/1. And since this new problem is just dividing a fraction by another fraction, we can use the keep-change-flip method as follows:

Step One: Keep the first fraction as is.

For the first step, simply keep the first fraction, 3/7, as is.

Step Two: Change the division sign to a multiplication sign.

For the second step, change the division sign (÷) into a multiplication sign (x) as follows:

  • 3/7 ÷ → 3/7 x

Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.

Finally, flip the positions of the numerator and the denominator of the second fraction as follows:

  • 2/1 → 1/2

The keep-change-flip process effectively transforms the division problem into an equivalent multiplication problem that is much easier to solve. This entire process is illustrated in Figure 09 below.

 

Figure 09: How to Divide a Fraction by a Whole Number: Rewrite the whole number as a fraction with a denominator of 1 and use the keep-change-flip method to solve.

 

Using the keep change flip method transforms the original division problem into an equivalent multiplication problem. To multiply two fractions together, simply multiply the numerators together and then multiply the denominators together as follows:

  • 3/7 x 1/2 = (3x1) / (7x2) = 3/14

Notice that the result, 3/14, can not be reduced. Therefore:

Final Answer: 3/14

The graphic in Figure 10 below details the entire process for solving this problem.

 

Figure 10: 3/7 x 1/2 = 3/14

 

In the next example, we will use the exact same process to divide a whole number by a fraction.

How to Divide a Whole Number by a Fraction: Example #2

Example #1: 9 ÷ 3/4

If we want to use the keep-change-flip method to divide a whole number by a fraction, then we will have to rewrite the whole number (9 in this case) as a fraction as follows:

  • 9 → 9/1

Now we can rewrite the original problem 9 ÷ 3/4 as 9/1 ÷ 3/4 (remember that these expressions are equivalent—i.e. they both mean the same thing). Now that we have two fractions being divided by each other, we can use keep-change-flip to solve.

Step One: Keep the first fraction as is.

Just like before, start by keeping the first fraction, 9/1, as is.

Step Two: Change the division sign to a multiplication sign.

Next, change the division sign (÷) into a multiplication sign (x) as follows:

  • 9/1 ÷ → 9/1 x

Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.

Finally, flip the numerator and the denominator of the second fraction as follows:

  • 3/4 → 4/3

The entire process of using keep-change-flip to transform this problem is illustrated in Figure 11 below.

 

Figure 11: How to Divide a Whole Number by a Fraction: Start by rewriting the whole number as a fraction and then use keep-change-flip to solve.

 

Now we can solve the problem by multiplying these two fractions together as follows:

  • 9/1 x 4/3 = (9x4) / (1x3) = 36/3 = 12

Notice that the result, 36/3, can be reduced. Since both the numerator and denominator are divisible by 3, we can conclude that the final answer is 12/1 or just 12.

Final Answer: 12

The graphic in Figure 12 further illustrates how we solved this problem.

 

Figure 12: How to divide a whole number by a fraction using keep-change-flip

 

Now that you know how to divide a fraction by a whole number and how to divide a whole number by a fraction, let’s move onto the final section where you will learn how to divide mixed fractions.

How to Divide Mixed Fractions

The final section of the How to Divide Fractions guide will focus on how to divide mixed fractions and how to divide fractions with mixed numbers.

Again, we can solve all of these types of problems by using the keep-change-flip method (click here to revisit the previous section).

Let’s get started with our first example!

How to Divide Fractions with Mixed Numbers: Example #1

Example #1: 5/9 ÷ 3 1/3

Whenever you have to divide fractions with mixed numbers, you can use the keep-change-flip method to find the answer. However, before you can use keep-change-flip, you will have to convert the mixed number into an improper fraction first.

In this example, we have to convert the fraction 3 1/3 into an improper fraction (a fraction whose numerator is greater than its denominator).

We can rewrite 3 1/3 as 10/3 because:

  • 3 1/3 = 3/3 + 3/3 + 3/3 + 1/3 = 10/3

If you need more help with converting mixed numbers into improper fractions, we highly recommend checking out this free guide before moving forward.

Now, we can rewrite the original problem as follows:

  • 5/9 ÷ 3 1/3 → 5/9 ÷ 10/3

Both of these expressions are equivalent to each other. The key difference here is that the new expression allows us to use the keep-change-flip method to solve it as follows:

Step One: Keep the first fraction as is.

As always, simply keep the first fraction, 5/9, as is.

Step Two: Change the division sign to a multiplication sign.

Next, change the division sign (÷) to a multiplication sign (x) as follows:

  • 5/9 ÷ → 5/9 x

Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.

Lastly, flip the positions of the numerator and the denominator of the second fraction as follows:

  • 10/3 → 3/10

Why are we doing this? Remember that the keep-change-flip method allows us to transform the original division problem into an equivalent multiplication problem that will be much easier to solve. This process is highlighted in Figure 13 below.

 

Figure 13: How to Divide Fractions with Mixed Numbers: Rewrite the mixed number as an improper fraction and then use keep-change-flip to solve.

 

From here, we can solve by multiplying these two fractions together as follows:

  • 5/9 x 3/10 = (5x3) / (9x10) = 15/90 = 1/6

Final Answer: 1/6

Figure 14 below illustrates how we were able to divide fractions with mixed numbers and solve this problem.

 

Figure 14: How to Divide Fractions with Mixed Numbers Explained

 

Now, let’s work through the final example of this guide where you will learn how to divide mixed fractions.

How to Divide Mixed Fractions: Example #2

Example #1: 6 1/2 ÷ 2 1/4

Just like the previous example, we can use the keep-change-flip method to solve this problem, but first we have to convert the mixed fractions in this problem into improper fractions.

In this case:

  • 6 1/2 = 2/2 + 2/2 + 2/2 + 2/2 + 2/2 + 2/2 + 1/2 = 13/2

  • 2 1/4 = 4/4 + 4/4 + 1/4 = 9/4

So, we can rewrite the original problem as:

  • 6 1/2 ÷ 2 1/4 → 13/2 ÷ 9/4

 

Figure 14: How to Divide Mixed Fractions: Start by rewriting any mixed fractions as improper fractions.

 

Again, if you need to review how to convert a mixed numbers into an improper fraction, we highly recommend checking out this free step-by-step guide.

Now, we have a new, yet equivalent, expression to be solved using keep-change-flip:

  • 13/2 ÷ 9/4

Step One: Keep the first fraction as is.

First, keep the first fraction, 13/2, as is.

Step Two: Change the division sign to a multiplication sign.

Second, change the division sign (÷) to a multiplication sign (x) as follows:

  • 13/2 ÷ → 13/2 x

Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.

And finally, flip the numerator and the denominator positions of the second fraction:

  • 9/4 → 4/9

 

Figure 15: How to Divide Mixed Fractions Explained

 

The last thing we have to do to solve this problem is multiply these two improper fractions together as follows:

  • 13/2 x 4/9 = (13x4) / (2x9) = 26/9 or 2 8/9

For this example, we are left we the improper fraction 26/9, which can not be reduced any further. You can also convert 26/9 into a mixed number, which would be 2 8/9. Both of these answers are equivalent.

Final Answer: 26/9 or 2 8/9

Figure 16 below shows how we found this final answer.

 

Figure 16: You will likely have to convert your final answer into a mixed number.

 

Conclusion: How to Divide Fractions

Dividing fractions can be a conceptually challenging math task, but learning how to use the keep-change-flip method can make the process much easier.

Whether you are dividing fractions with other fractions, fractions with whole numbers, whole numbers with fractions, or fractions with mixed numbers, the keep-change-flip method provides a simple three-step process for solving these types of problems.

The keep-change-flip method for dividing fractions can be summarized as follows:

  • Step One: Keep the first fraction as is.

  • Step Two: Change the division sign to a multiplication sign.

  • Step Three: Flip the position of the numerator and the denominator in the second fraction.

After you perform keep-change-flip, you can solve the problem by multiplying and reducing the result whenever possible.

Search Tags: how to subtract fractions, subtracting fractions, how to subtract fractions with different denominators, fraction subtraction, subtracting fractions with unlike denominators, how do you subtract fractions?

1 Comment

How to Round to the Nearest Thousandth—Step-by-Step Guide

Comment

How to Round to the Nearest Thousandth—Step-by-Step Guide

How to Round to the Nearest Thousandth

Rounding to the Nearest Thousandth in 3 Easy Steps

 

Free Step-by-Step Guide: How to round to the nearest thousandth.

 

Learning how to correctly round numbers, especially numbers with decimals, is an important math skill that will help you to work with numbers, make accurate estimations, and solve problems.

Many students find rounding to be a relatively easy skill to learn when it comes to working with whole numbers, but many of those same students will struggle with rounding once decimals are involved. However, while rounding decimal numbers may seem trickier than rounding whole numbers, the process remains the same and learning how to round to the nearest thousandth decimal place is a math skill that every student can easily learn.

Ready to learn how to round to the nearest thousandth? This free step-by-step guide will show you how to round to the nearest thousandth by working through six different practice problems together. By working through each problem together, you will gradually learn everything you need to know about rounding to the nearest thousandth to the point that you will be able to solve decimal rounding problems with ease.

For this guide on rounding, you can work through each section in order, or you can use the quick links below to jump to a particular section of interest:

(Looking for help with rounding to the nearest tenth and rounding to the nearest hundredth?)

What is Rounding?

In math, the process of rounding involves taking a given number and rewriting it as a new number that serves as a close estimation of its actual value. Why? Because, mathematically speaking, doing so makes the original number easier to work with.

Consider a smoothie that costs $7.95. By rounding to the nearest whole number (or whole dollar in this case), you could say that the cost of a smoothie is $8. If you had to figure out the cost of 13 smoothies, without rounding, you would have to calculate 7.95 x 13 = ?, which isn’t exactly the easiest multiplication problem to solve in your head. On the other hand, if had to figure out the cost of 13 smoothies after rounding $7.95 to $8, you can determine close estimate of the actual cost simply by performing 8 x 13 = $104. So, you could say that the approximate cos of 13 smoothies would be $104.

  • Actual Cost: 7.95 x 13 = $103.35

  • Estimated Cost: 8.00 x 13 = $104.00

Notice how rounding made this problem much easier to solve and the difference between the actual cost and the estimated cost is relatively small.

The key takeaway here is that rounding a mathematical tool that you can use to estimate values and make them easier to work with and perform operations on.

 

Figure 01: The process of rounding involves taking a given number and rewriting it as a new number that serves as a close estimation of its actual value

 

Rounding Up vs. Rounding Down

Next, let’s run through a quick refresher on the difference between rounding up and rounding down.

You probably already know that, when it comes to rounding, the number 5 is a big deal. Why?

Rounding Rule: If the number directly to the right of the number you are rounding is greater than or equal to 5, then you will round up. Conversely, if the number directly to the right of the number you are rounding is less than or equal to 4, then you will round down.

As far as rounding rules go, this is the only true definition that you will need to remember if you want to learn how to successful round to the nearest thousandth. And, this rule will apply to any rounding problem you will come across, so make sure that you have a firm understanding of it before moving on.

Reminder:

  • If the number directly to the right of the number you are rounding is ≥ 5 → round up

  • If the number directly to the right of the number you are rounding is ≤ 4 → round down

Let’s consider two simple examples:

Example A: Round 128 to the nearest ten.

In this example, 2 is in the tens decimal place and the number 8 is directly to the right of it. Since 8 ≥ 5, you will have to round up the 2 as follows:

  • 128 → 130

Example B: Round 254 to the nearest ten.

In this example, 5 is in the tens decimal place and the number 4 is directly to the right of it. Since 4 ≤ 4, you will have to round down the 5 as follows:

  • 254 → 250

 

Figure 02: Whenever the number directly to the right of the number you are rounding is ≥ 5, you have to round up. Otherwise, round down.

 

3-Step Process: How to Round to the Nearest Thousandth

Now that you understand what it means to round a number and the difference between rounding up and rounding down, you are ready to learn how to round to the nearest thousandth and work through some practice problems.

For all of the rounding to the nearest thousandth examples in this guide, we will be using the following 3-step process for rounding to the nearest thousandth:

  • Step #1: Locate and underline the value in the thousandths place value slot

  • Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

  • Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

It’s ok if this 3-step process seems complicated at first glance. After working through a few examples, you will become much more comfortable with using these three steps to solve decimal rounding problems with ease

Example #1: Round to the Nearest Thousandth: 5.3641

Let’s go ahead and dive into our first example where we are tasked with rounding 5.3641 to the nearest thousandth.

We will solve this problem (and all of the practice problems in this guide) using the previously described 3-step process as follows:

Step #1: Locate and underline the value in the thousandths place value slot

For the number 5.3641, there are four numbers to the right of the decimal place. The third number to the right of the decimal place will always be the thousandths place value slot, which, in this example, is the number 4.

Locating and underlining the value in the thousandths place vale slot is illustrated in Figure 03 below.

 

Figure 03: How to round to the nearest thousandth: The first step is to identify the thousandths place value slot.

 

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

Next, take a look at the number directly to the right of the 4 in the thousandths place value slot.

In this example, that number is 1, which is ≤ 4.

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

Since the number directly to the right of the 4 in the thousandths place value slot is 1, which is ≤ 4, you will have to round down.

In this case, rounding down means that the 1 to the right of the 4 in the thousandths place value slot becomes a zero and effectively disappears, which leaves us with:

Final Answer: 5.3641 rounded to the nearest thousandth is 5.364

The complete process of solving this first example is shown in Figure 04 below:

 

Figure 04: When rounding down, the number to the right of the thousandths decimal slot becomes a zero and disappears.

 

Example #2: Round to the Nearest Thousandth: 5.3648

For the next example, you will notice that the number in question is very similar to the previous example. In this case, the only difference is that the final number is an 8 rather than a 1.

How will this difference effect the final answer? Let’s apply our 3-step process and see:

Step #1: Locate and underline the value in the thousandths place value slot

For this example, the number 4 is in the thousandths place value slot as shown in Figure 05 below.

 

Figure 05: How to round to the nearest thousandth: Start by identifying the value in the thousandths decimal slot.

 

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

In this example, the number directly to the right of the 4 in the thousandths place value slot is 8.

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

The number directly to the right of the 4 in the thousandths place value slot is 8, and 8≥ 5, so this time we will be rounding up.

When rounding up, you will add one to the value in the thousandths place value slot (4 in this example) and all numbers to the right of it will disappear.

Final Answer: 5.3648 rounded to the nearest thousandth is 5.365

This process of solving Example #2 is illustrated in Figure 06 below.

 

Figure 06: 5.3648 rounded to the nearest thousandth is 5.365

 

Before moving onto more practice problems, let’s take a closer look at the differences between rounding the numbers in Example #1 and Example #2 to the nearest thousandth:

  • Example #1: 5.3641 → 5.364 (we rounded down)

  • Example #2: 5.3648 → 5.365 (we rounded up)

The graphic in Figure 07 below further highlights the differences between how we solved these first two examples (namely, the difference between solving by rounding down and solving by rounding up).

 

Figure 07: Examples of rounding down vs. rounding up.

 

Example #3: Round to the Nearest Thousandth: 1.27025

Moving onto this next example, you will notice that the number 1.27025 includes five digits to the right of the decimal point. However, whenever you are rounding to the nearest thousandth, you will only need to first four digits and anything beyond that can be ignored.

To see this process in action, let’s go ahead and apply our 3-step process for rounding to the nearest thousandth.

Step #1: Locate and underline the value in the thousandths place value slot

For the number 1.27025, the number 0 is in the thousandths place value slot, as shown in Figure 08 below.

 

Figure 08: Remember that you only need the first four digits the right of the decimal point to round a number to the nearest thousandth. Anything beyond that can be ignored.

 

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

Next, notice that 0 is in the thousandths place value slot and the number directly to the right of it is a 2, which is ≤ 4.

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

Since 2 ≤ 4, we will be rounding down to solve this problem as is shown in Figure 09 below:

Final Answer: 1.27025 rounded to the nearest thousandth is 1.270

 

Figure 09: 1.27025 rounded to the nearest thousandth is 1.270

 

Example #4: Round to the Nearest Thousandth: 24.3759414

Again, we can solve this problem by applying our 3-step process. Just remember that you can ignore any numbers that come after the fourth number to the right of the decimal point.

Step #1: Locate and underline the value in the thousandths place value slot

For the number 24.3759414, the number 5 is in the thousandths place value slot.

 

Figure 10: The number 5 is in the thousandths place value slot.

 

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

The number directly to the right of the 5 is 9, and 9 ≥ 5.

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

Since 9 ≥ 5, you must round it up to solve this problem and conclude that:

Final Answer: 24.3759414 rounded to the nearest thousandth is 24.376

Figure 11 below illustrates the entire 3-step process for rounding Example #4 to the nearest thousandth.

 

Figure 11: 24.3759414 rounded to the nearest thousandth is 24.376

 

Example #5: Round to the Nearest Thousandth: 18.34951

Are you starting to get the hang of it? Let’s continue onto another example.

Step #1: Locate and underline the value in the thousandths place value slot

For the number 18.34951, the digit in the thousandths place value slot is 9.

 

Figure 14: How to Round to the nearest Thousandth: The digit in the thousandths place value slot is 9.

 

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

Next, the number directly to the right is 5, and 5 ≥ 5.

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

Since 5 ≥ 5, we know that we have to take the 9 in the thousandths place value slot and round it up. But how do you round up the number 9 without turning it into a 10?

Rule: Whenever you are rounding up the number 9, you have to turn it into a zero and add one to the number directly to the left of the 9.

Figure 13 below illustrates the application of this rule being used to solve Example #5.

Final Answer: 18.34951 rounded to the nearest thousandth equals 18.350

 

Figure 13: Whenever you are rounding up the number 9, you have to turn it into a zero and add one to the number directly to the left of the 9.

 

Example #6: Round to the Nearest Thousandth: 0.023499

You made it to the final example! To solve this last problem, we will again rely on our 3-step process as follows:

Step #1: Locate and underline the value in the thousandths place value slot

In this example, 0.023499, the number 3 is in the thousandths place value slot.

 

Figure 14: Reminder: When it comes to rounding to the nearest thousandth, you can ignore any additional numbers after the fourth digit to the right of the decimal point.

 

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

Notice that the number directly to the right of the 3 is a 4.

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

Since 4 ≤ 4, we know that we have to round down to solve this problem.

Final Answer: 0.023499 rounded to the nearest thousandth is 0.023

 

Figure 15: Rounding 0.023499 to the nearest thousandth.

 

Conclusion: Round to the Nearest Thousandth

Rounding numbers, especially decimals, is an extremely important and useful math skill that helps students to estimate numbers and make calculations with them.

This guide specifically focused on rounding to the nearest thousandth, where you learned and applied a simple 3-step method to rounding any number to the nearest thousandth decimal place:

Step #1: Locate and underline the value in the thousandths place value slot

Step #2: Identify if the number directly to the right is ≥ 5 or ≤ 4

Step #3: If the number directly to the right is ≥ 5, round up the number in the thousandths place value slot. If the number directly to the right is ≤ 4, round down the number in the thousandths place value slot to zero.

You can use this 3-step process to solve any problem where you have to round a given number to the nearest thousandth! So, it should be no surprise that we were able to use it to solve all six practice problems in this guide and make the following conclusions:

  • 5.3641 → 5.364

  • 5.3648 → 5.365

  • 1.27025 → 1.270

  • 24.3759414 → 24.376

  • 18.34951 → 18.350

  • 0.023499 → 0.023

Need some extra practice? If so, we strongly recommend that you go back and work through the practice problems in this guide again. The more that you practice, the more comfortable you will become with the 3-step process. And, if you need some additional practice beyond this guide, check out the free rounding worksheets and answer keys available on our free math worksheet libraries.

Keep Learning:

How to Round to the Nearest Hundredth (Step-by-Step Guide)

Continue your rounding journey by learning how to round to the nearest hundredth.

Comment