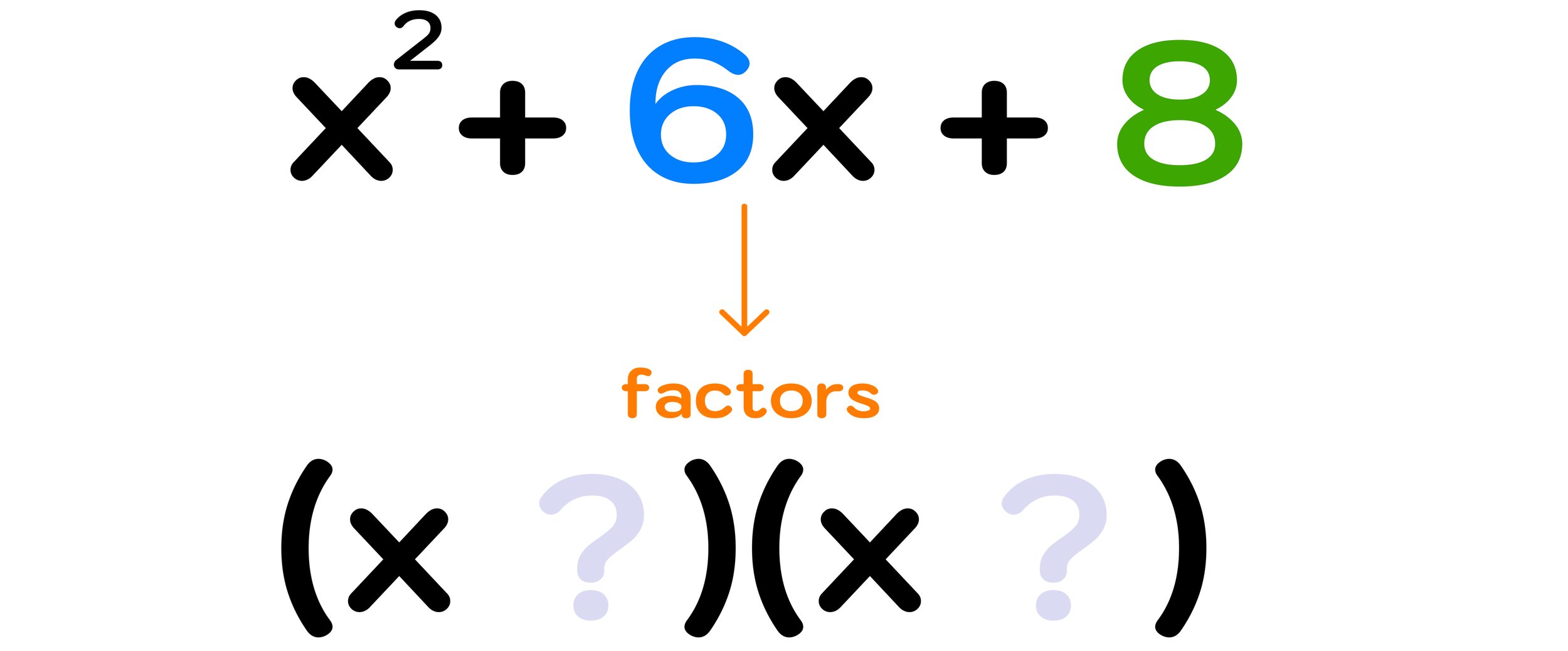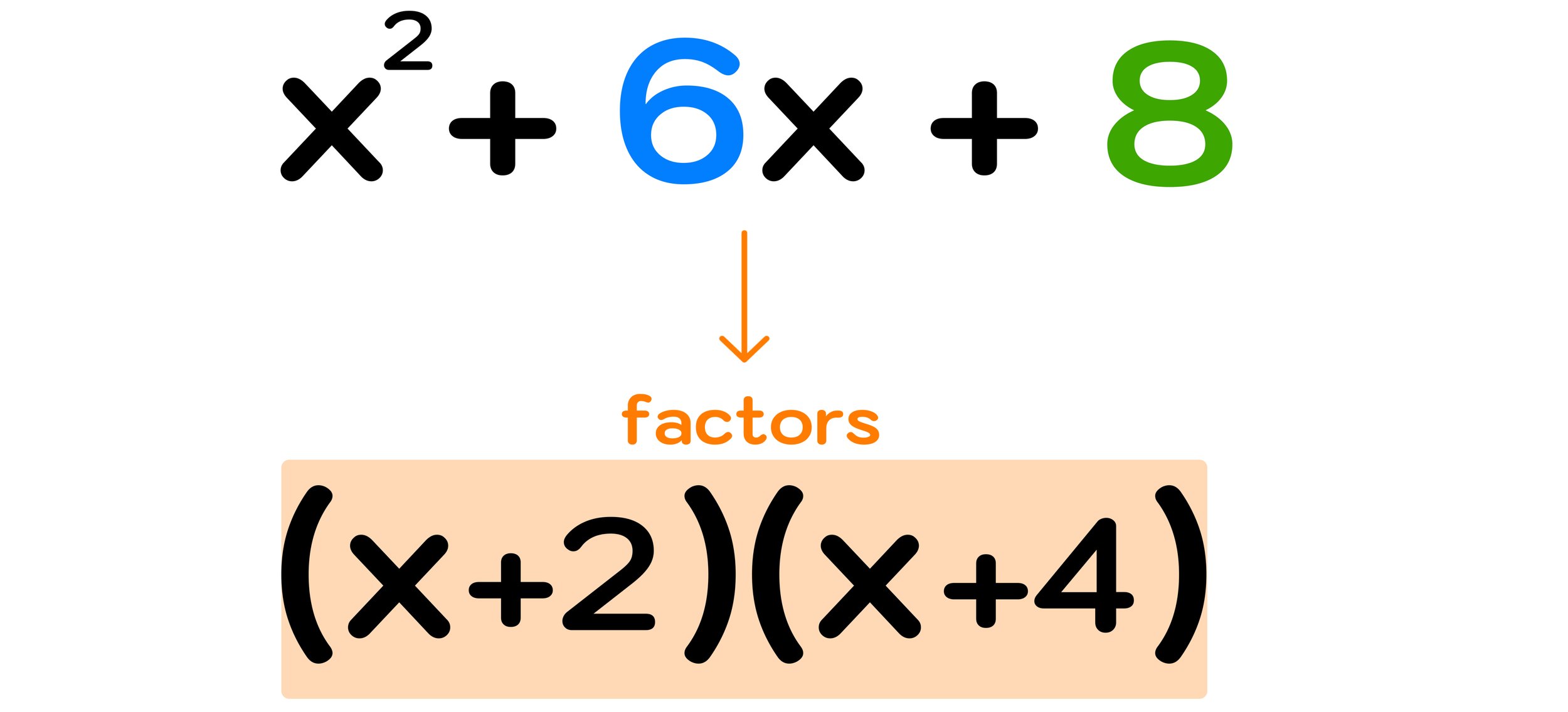Are Timed Math Tests Harmful to Students?

Are Timed Math Tests Harmful to Students?

How Timed Math Tests Lead to Math Anxiety and Poor Results

Students with math anxiety are often affected by feelings of tension, apprehension, or fear, which interfere with learning or remembering math facts and skills. (Image: Mashup Math MJ)

Question: Which of these statements best describes an exceptional math student?

• She performs computations faster than her classmates.

• She has memorized lots of facts, formulas, and procedures.

• She scores high grades on exams and works well under pressure.

• She understands number relationships and how to solve complex problems.

If you chose one of the first three statements, then your beliefs about the essence of math understanding may be rooted in misconceptions.

People often allow the prevalence of high-stakes exams to frame mathematics education into a practice in rote memorization and uninspired computations.

As a result, many students lose interest in learning math at a young age.

Large populations of students believing that they can't understand mathematics only breeds more misconceptions, such as the idea that only certain individuals are capable of understanding math.

However, we now know that the idea that only certain people are capable of understanding math is a myth. According to a recent report, The Myth of 'I'm Bad at Math', by The Atlantic, math ability can be improved through effort and learning with a growth mindset.

The truth is that, under the right conditions, anyone can develop math skills.

Are timed math tests harmful to students? (Image: Mashup Math FP)

Where Does the "Math Person" Myth Come From?

A large part of the answer lies in how schools use testing.

The demands of high-stakes exams, which often overpower curriculums, can be felt in math classrooms across the country.

According to a recent report on standardized exams by the Washington Post:

The average student in America’s big-city public schools takes some 112 mandatory standardized tests between pre-kindergarten and the end of 12th grade — an average of about eight a year, the study says. That eats up between 20 and 25 hours every school year.

The frequency of testing is only part of the problem.

Teachers are confined by strict curriculum schedules that force the pace of instruction and assessment.

Under these conditions, teachers are forced to give timed tests that emphasize speed and computation over deep mathematical thinking.

Image: Mashup Math MJ

What are the Consequences of Time Pressure?

Our time-bound approach to testing often leads to math anxiety.

Students with math anxiety are affected by feelings of tension, apprehension, or fear, which interfere with learning or remembering math facts and skills.

And, the problem is only becoming worse.

According to a recent study by the University of Chicago, math anxiety has now been documented in children as young as five, and timed tests are a key cause of this weakening, often lifelong condition.

Timed tests elicit such powerful emotions that students believe that being fast with math facts is the heart of the subject.

The misconception that speed and memorization are the keys to understanding math has resulted in high numbers of students dropping out of math and the depressed numbers of women in STEM-based college majors.

The negative impact of math anxiety is holding back crowds of students in the United States, which continues to be outpaced by other countries.

According to a recent report on global math and science rankings by NPR:

In mathematics, 29 nations and other jurisdictions outperformed the United States by a statistically significant margin, up from 23 three years ago.

Math students in the U.S. can't compete with their global counterparts until they are freed from the debilitating effects of math anxiety.

Image: Mashup Math FP

What Does Math Anxiety Do to the Brain?

Stanford researcher and math education expert, Jo Boaler, has shed much-needed light on the consequences of timed testing in her reports on YouCubed.org, a Stanford-funded organization that focuses on, according to their website, transforming the latest research on math learning into accessible and practical forms.

Boaler points to brain science research suggesting that speed and time pressure blocks working memory, which is where math facts are stored in the brain.

When the working memory is blocked, students become unable to retrieve what they already know.

This inability to recall information under pressure is the hallmark of math anxiety.

According to Boaler's Report on Time Pressure Blocking Working Memory:

Conservative estimates suggest that at least a third of students experience extreme stress related to timed tests, and these are not students from any particular achievement group or economic background. When we put students through this anxiety-provoking experience, they distance themselves from mathematics.

If we continue to assess mathematical understanding using timed tests, then we will continue to turn students away and perpetuate misconceptions.

Image: Mashup Math MJ

How Can We Help Our Students?

The best way to learn math facts is through mathematical activities that focus on understanding number relationships.

This authentic understanding is difficult to achieve in a time-bound environment.

Yet, many people believe that mathematics is only about calculating and recalling math facts -- and that the best mathematical thinkers are those who can calculate the quickest.

In truth, skilled mathematicians are often slow with performing math, because they take the time to think carefully and deeply about mathematics.

If we want our students to become powerful thinkers--ones who can make connections, think logically, and solve complex problems--then systemic changes must be made.

You can take action today by removing or, at the very least, reducing timed tests from your classroom and providing ample opportunities for students to engage in deep mathematical thinking.

You can also keep this conversation going.

In your school. In your classroom. And in your home.

Math education is evolving and the movement towards removing timed testing is building momentum, but it will take a group effort to make real change.

More Math Education Resources You Will Love:

How to Simplify Radicals in 3 Easy Steps

How to Simplify Radicals in 3 Easy Steps

Math Skills: How to Simplify a Radical Using a 3-Step Strategy

Every math student must learn how to work with numbers inside of a radical (√) at some point. While working with perfect squares inside of radicals can be quite easy, the task becomes a bit trickier when non-perfect squares are involved and you have to simplify.

While learning how to simplify a radical of a non-perfect square may seem challenging, it’s actually a relatively easy math skill to learn as long as you have a strong understanding of perfect squares and factoring (we will review both of these topics in this guide).

This free How to Simplify Radicals Step-by-Step Guide will teach you how to simplify a radical when the number inside of it is not a perfect square using a simple 3-step strategy that you can use to solve any problem involving simplifying radicals.

The following topics and examples will be covered in this guide:

• What is the difference between a perfect square and a non-perfect square?

• How to Simplify Radicals: 3-Step Strategy Explained

• How to Simply a Radical Example #1

• How to Simply a Radical Example #2

• How to Simply a Radical Example #3

You can use the quick-links above to jump to any section of this guide. However, we highly recommend that you work through each section in order, including the following review section where we will quickly recap some important features of perfect squares, non-perfect squares, factors, and the properties of radicals. This review will recap some important vocabulary terms and prerequisite math skills that you will need to be successful with this new math skill.

But, before you learn how to add fractions, let’s do a quick review of some key characteristics and vocabulary terms related to fractions before we move onto a few step-by-step examples of how to add fractions.

Let’s get started!

Radicals, Perfect Squares, and Non-Perfect Squares

Before you learn how to simplify a radical, it’s important that you understand what a radical is and what the difference between a perfect square and a non-perfect square is.

Definition: In math, a radical (√) is a symbol that is associated with the operation of finding the square root of a number.

Finding the square root of a number means finding an answer to the question: “What number times itself results in the original number?” For example, the square root of 25 (or √25) is equal to 5 because 5 times 5 equals 25.

Definition: In math, a perfect square is a number that is the square of any integer. This means that a perfect square is a number that can be represented as the product of an integer squared (or an integer multiplied by itself). For example, 36 is a perfect square because 6 times 6 equals 36.

Note that perfect squares are unique and there are not that many of them. In fact, most numbers are considered non-perfect squares because they can not be represented as an integer times itself.

Figure 01: What is a perfect square?

Definition: In math, a non-perfect square is a number that is not the square of any integer. This means that a non-perfect square is a number that can’t be represented as the product of an integer squared (or an integer multiplied by itself). For example, 20 is not a non-perfect square because it is impossible to take an integer and multiply by itself to get a result of 20.

Again, most numbers are non-perfect squares. When we see these types of numbers inside of a radical, they can be simplified or expressed as decimal numbers, but never as an integer.

The chart in Figure 02 below shows all of the perfect squares and non-perfect squares up to 144. Note that the numbers highlighted in orange are all perfect squares. For example:

• 49 is a perfect square (because 7 x 7 = 49)

• 8 is a non-perfect square

Figure 02: Before you learn how to simplify a radical, you must be familiar with the perfect squares.

For quick reference, here is a list of the perfect squares up to 144:

• 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144

Now that you are familiar with radicals, perfect squares, and non-perfect squares, you are ready to learn how to simplify radicals.

---

How to Simplify Radicals in 3-Easy Steps

Now you are ready to learn how to simplify a radical using our easy 3-step radical.

Let’s start by considering a problem where you are asked to simplify c. You should notice that 16 is a perfect square, so you can easily conclude that √16 = 4 (because 4 x 4 =16).

This kind of problem is pretty easy when the number inside of the radical is a perfect square, but what happens when it is not a perfect square? For example, what if you were dealing with a non-perfect square like 12 inside of the radical? How can you simplify √12? This guide will teach you how to do just that (i.e. how to simplify a radical containing a non-perfect square).

To simplify radicals like √12, we will use the following 3-step strategy:

• Step One: List all of the factors of the number inside of the radical

• Step Two: Determine if any of the factors are perfect squares (not including 1). If there are multiple perfect squares, choose the largest one.

• Step Three: Separate the original radical into two radicals and simplify.

Does this sound confusing? The process gets easier with practice. Let’s go ahead and apply these three steps to √12 as follows:

Step One: List all of the factors of the number inside of the radical

First, we will list all of the factors of 12:

• Factors of 12: 1, 2, 3, 4, 6, 12

Step Two: Determine if any of the factors are perfect squares (not including 1). If there are multiple perfect squares, choose the largest one.

From the list of factors above, we can see that only 4 is a perfect square and it is the only perfect square that is a factor of 12. This is important because we will need to find at least one factor that is a perfect square in order to simplify a radical of a non-perfect square.

• 4 is a factor of 12 and a perfect square

• 4 x 3 = 12

Figure 03: How to split up a radical.

Step Three: Split the original radical into two radicals and simplify.

For the final step, what do we mean by “split up the radical”?

Figure 03 above illustrates the following property of radicals:

• √(ab) = √a x √b (as long as a>0 and b>0)

This means that you can separate a radical into the radicals of two of its factors. In the case of √12, we can rewrite it as follows:

• √12 = √(4 x 3) = √4 x √3

Now, notice that √4 is equal to 2 (because 4 is a perfect square), so we can rewrite the result as follows:

• √12 = = √4 x √3 = 2 x √3

From here, we can not simplify this radical any further, so we can conclude that:

Final Answer: √12 = 2√3

Figure 04 below illustrates how we solved this problem using our 3-step strategy:

Figure 04: How to Simplify Radicals in 3 Easy Steps.

Now that you have learned the 3-step strategy for how to simplify radicals, let’s gain some experience using this strategy to solve a few practice problems.

---

How to Simplify Radicals Example #1

Example #1: Simplify √72

For this first example (and all of the examples in this guide) we will use our 3-step strategy to simplify the given radical as follows:

Step One: List all of the factors of the number inside of the radical

For the first step, let’s list all of the factors of 72:

• Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72

Step Two: Determine if any of the factors are perfect squares (not including 1). If there are multiple perfect squares, choose the largest one.

Next, take a look at the list of factors of 72. Notice that 72 has three facts that are perfect squares other than 1: 4, 9, and 36. In cases like this, you have to choose the largest perfect square, which is 36 for this example.

• 36 is a factor of 72 and 36 is a perfect square

• 36 x 2 = 72

Step Three: Split the original radical into two radicals and simplify.

Finally, we can split the radical into the radicals of two of its factors (namely 36 and 2) as follows:

• √72 = √(36 x 2) = √36 x √2

Since 36 is a perfect square (36 = 6x6), we know that √36=6, so we can say that:

• √72 = = √36 x √2 = 6 x √2

Now we can make the following conclusion:

Final Answer: √72 = 6√2

Figure 05 below illustrates how we simplified √72 for this first example.

Figure 05: How to Simplify Radicals Explained

Let’s continue onto another practice problem!

---

How to Simplify Radicals Example #2

Example #2: Simplify √48

Just as we did in the previous example, we can use our 3-step strategy to simplify √48 as follows:

Step One: List all of the factors of the number inside of the radical

Let’s start by listing all of the factors of 48:

• Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48

Step Two: Determine if any of the factors are perfect squares (not including 1). If there are multiple perfect squares, choose the largest one.

For the next step, notice that 48 has two perfect square factors other than one: 4 and 16. Remember that, if we want to simplify completely, we must choose the largest perfect square factor, which, in this case, is 16.

• 16 is a factor of 48 and 16 is a perfect square

• 16 x 3 = 48

Step Three: Split the original radical into two radicals and simplify.

Lastly, we have to split the radical into the radicals of two of its factors where one of them is a perfect square (in this example, the perfect square factor is 16 and the non-perfect square factor is 3).

• √48 = √(16 x 3) = √16 x √3

Since 16 is a perfect square (16 = 4x4), we can rewrite √16 as 4:

• √48 = √16 x √3 = 4 x √3

And now we have our final answer:

Final Answer: √48 = 4√3

Figure 06 below shows how we used our 3-step strategy to simplify the radical √48.

Figure 06: How to Simply a Radical: √48 = 4√3

Are you feeling better about using our 3-step strategy to simplify radicals? Let’s move on and work through one more example.

---

How to Simplify Radicals Example #3

Example #3: Simplify √320

For this final example, we have to simplify a radical with a triple-digit non-perfect square inside of it: √320. We can do just that by using our 3-step strategy:

Step One: List all of the factors of the number inside of the radical

Start by listing all of the factors of the number inside of the radical, which, in this case, is 320:

• Factors of 48: 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 64, 80, 160, 320

Step Two: Determine if any of the factors are perfect squares (not including 1). If there are multiple perfect squares, choose the largest one.

Next, identify all of the perfect square factors of 320 other than 1. In this case, we have 4, 16, and 64. The largest of these three perfect square factors is 64.

• 64 is a factor of 320 and 64 is a perfect square

• 64 x 5 = 320

Step Three: Split the original radical into two radicals and simplify.

For the very last step, we must split the radical √320 into the radicals of two of its factors. For this third example, the perfect square factor is 64 and the non-perfect square factor is 5.

• √320 = √(64 x 5) = √64 x √5

Since 64 is a perfect square (64 = 8x9), we can rewrite √64 as 8:

• √320 = √64 x √5 = 8 x √5

All that we left to do is conclude that:

Final Answer: √320 = 8√5

The graphic in Figure 07 below illustrates how we solved this problem using our 3-step strategy.

Figure 07: How to Simply Radicals: √320 = 8√5

---

Conclusion: How to Simplify Radicals in 3 Easy Steps

Whenever you have to simplify a radical with a non-perfect square inside, you have to find two factors of that number, one of which must be a perfect square. Once you find two factors that meet these conditions, you can simplify the perfect square and rewrite the radical in simplified form.

The process of simplifying radicals of non-perfect squares can done by following these three steps:

• Step One: List all of the factors of the number inside of the radical

• Step Two: Determine if any of the factors are perfect squares (not including 1). If there are multiple perfect squares, choose the largest one.

• Step Three: Separate the original radical into two radicals and simplify.

As long as you can follow these steps, you can learn how to simplify radicals and you can solve a variety of problems.

Keep Learning:

How to Subtract Fractions in 3 Easy Steps

---

Free Printable Math Puzzles for Middle School Students

Are you looking for some fun, printable math puzzles for middle school students?

These 5 math puzzles will engage your students and get them thinking creatively and visually about math topics including fractions, areas models, the order of operations, and even algebra!

So, can your middle schoolers solve these fun middle school math puzzles? Let’s get started and find out!

---

Math Puzzles for Middle School Students #1

This first math puzzle for middle school challenges students to use their knowledge of the order of operations to find the value of each symbol (the hamburger, the taco, and the pizza) and the ‘?’ in the puzzle below.

Solution: Pizza = 3, Hamburger = 2, Taco = 8

---

Math Puzzles for Middle School Students #2

The second math puzzle is a Multiplication Table activity where students have to use their knowledge of multiplication and multiplication facts to find the value of each symbol in the grid below.

Solution: Volcano = 1, Statue of Liberty = 3, Rocket = 6, Race Car = 2, Ferris Wheel = 18

---

Math Puzzles for Middle School Students #3

Our third math puzzle for middle school students is a math logic puzzle that challenges students to use their number sense to recognize numerical patterns to solve the puzzle.

Solution: Multiple solutions exist using each value only once.

---

Math Puzzles for Middle School Students #4

The next middle school math puzzle is an area model problem where students have to find the value of each symbol to complete the area model and determine which two numbers are being multiplied together.

Solution: Pretzel = 8, Mustard = 3, Chocolate-Covered = 50, Salt = 40, Sticks = 24

---

Math Puzzles for Middle School Students #5

The final math puzzle for middle school students is a fraction model puzzle where students are tasked with using their knowledge of fractions to find the value of each symbol.

Solution: Pink = 16, Chocolate = 8, Purple = 2, Ice Cream Cup = 24, Ice Cream Cone = 3

---

Are you looking for more daily math challenges and puzzles to share with your kids?

My best-selling workbook 101 Math Challenges for Engaging Your Students in Grades 3-8 is now available as a PDF download. You can get yours today by clicking here.

---

Read More Posts About What’s Trending in Math Education:

How to Factor Quadratic Equations—Step-by-Step Examples and Tutorial

How to Factor Quadratic Equations Explained

Step-by-Step Guide: How to Factor a Quadratic Equation, How to Solve Quadratic Equations by Factoring

Step-by-Step Guide: How to factor a quadratic equation explained.

In algebra, a quadratic equation is an equation of the form ax² + bx + c = 0 where a can not equal zero.

The word quad is Latin for four or fourth, which is why a quadratic equation has four terms (ax², bx, c, and 0). Being able to solve quadratic equations by factoring is an incredibly important algebra skill that every student will need to learn in order to be successful in Algebra I, Algebra II, and beyond. Learning how to factor a quadratic equation comes down to being able to recognize a quadratic equation, being able to factor it, and then finally being able to solve for x and check your answer for mistakes.

This free Step-by-Step Guide on How to Factor Quadratic Equations will cover the following topics:

• What is a Quadratic Equation?

• What are the Solutions of a Quadratic Equation?

• How to Factor Quadratic Equations when a=1

• How to Factor Quadratic Equations when a≠1?

Note that this guide is a follow-up to our free step-by-step guide How to How to Factor Polynomials, which reviews how to factor polynomials with 2 terms, 3 terms, and 4 terms. While we will review general factoring in this guide, we will be more focused on how to factor a quadratic equation.

However, before we learn how to factor quadratic equations and how to solve quadratic equations by factoring, let’s quickly review some important vocabulary terms related to quadratics and quadratic equations.

Figure 01: What is the difference between a trinomial expression and a quadratic equation.

What is a Trinomial Expression?

While the focus of this guide is on teaching you how to factor quadratic equations and how to solve quadratic equations by factoring, it is important that you first understand how the difference between a trinomial expression and a quadratic equation.

In algebra, a trinomial expression is a polynomial with 3 terms of the form ax² + bx + c. Note that, since it is an expression, a trinomial does not include an equal sign.

• ax² + bx + c

What is a Quadratic Equation?

In algebra, a quadratic equation is a trinomial of the form ax² + bx + c that is equal to zero. So, we can say that a quadratic equation is of the form:

• ax² + bx + c = 0

Figure 01 above illustrates this key difference between trinomial expressions and quadratic equations, which is namely that a quadratic equation is an equation and includes a fourth term (=0).

Why are we concerned with quadratic equations being equal to zero? You may already know that, when graphed, quadratic equations can be represented on the coordinate plane as a parabola (a U-shaped curved). When we solve quadratic equations by factoring, we are actually figuring out where the parabola crosses zero on the x-axis, as shown in Figure 02 below.

Figure 02: By setting a quadratic equation equal to zero, we are able to determine where the parabola crosses the x-axis. These x-values will be the solution(s) to a quadratic equation. This guide will teach you how to solve quadratic equations by factoring (not graphing).

Consider the example quadratic in Figure 02 above:

• x² +6x + 8 = 0

Notice that, for this quadratic equation, a=1, b=6, and c=8. When it comes time to learn how to factor a quadratic equation later on, it will be important that you are able to identify the values of a, b, and c for any given quadratic equation.

Now, here are two key pieces of information about the solutions to quadratic equations:

• The solution(s) to any quadratic equation are the points where the graph of the quadratic crosses the x-axis on a graph.

• Quadratic equations typically have two solutions, but they can also have one solution or zero solutions.

• You do not have to graph quadratic functions to solve them. You can solve quadratic equations by factoring.

Now that you understand what the solutions of a quadratic represent graphically, you are ready to learn how to factor equations and solve them algebraically.

Are you ready to get started?

---

How to Factor Quadratic Equations: Intro

Let’s start by factoring the example quadratic equation from Figure 02 above: x² +6x + 8 = 0

Example #1: Factor and Solve x² +6x + 8 = 0

From our graph, we already know that this quadratic equation will have two solutions: x=-4 and x=-2 (note that this can also be written as x={-4,-2}). So, let’s use factoring to find these answers algebraically.

To factor a quadratic equation, we can split it up into two parts:

• The left side of the equal sign

• The right side of the equal sign

On the left side of the equal sign, we must have a trinomial of the form ax² + bx + c to deal with and, on the right side, we must have a zero. If the quadratic equation in question is not in this form, we will have to use algebra to rearrange it. However, this first example is good to go so we don’t have to move any of the terms around. This first step is shown in Figure 03 below:

Figure 03: How to factor a quadratic equation.

From here, the next step is to factor the trinomial on the left side of the equal sign:

• x² +6x + 8

Note that, for this introductory example, the value of a (the leading coefficient) is 1. When this is the case, you can factor the trinomial on the left-side of the equation as follows:

Figure 04: How to solve quadratic equations by factoring.

Step One: Identify the values of b and c.

In this example, the values of b and c are: b=6 & c=8

Step Two: Find two numbers that both ADD to b and MULTIPLY to c.

Once you have identified the values of b and c (6 and 8 respectively in this example), you can use trial-and-error to find two numbers that both add to the b term (6) and multiply to the c term (8). Another way to say this is: find two numbers with a sum of 6 and a product of 8.

For example, let’s say that you chose the numbers 5 and 1. In this case, 5+1=6, but 5x1≠ 8, so these two numbers would not work.

• 5 + 1 =6 (the value of b) ✓

• 5 x 1 ≠ 8 (the value of c) ✘

However, if you chose the numbers 2 and 4:

• 2 + 4 =6 (the value of b) ✓

• 2 x 4 = 8 (the value of c) ✓

Since the sum of 2 and 4 is 6 and the product of 2 and 4 is 8, you can found out that the factors of the trinomial x² + 6x + 8 are (x+2) and (x+4)

Step Three: Use your numbers from step two to write out the factors

In this case, you can conclude that the factors of x² + 6x + 8 are (x+2) and (x+4).

Figure 05: x² + 6x + 8 = (x+2)(x+4).

How do you know if you result is correct? You can check your answer by performing double distribution as follows:

• (x+2)(x+4) = x² + 2x + 4x + 7 = x² + 6x + 8

If the result is the same trinomial that you started with, then you know that your factors are correct.

Figure 06: How to Solve a Quadratic Equation by Factoring

Now we have a new equation:

• (x+4)(x+2)=0

This is not our final answer. To solve this quadratic by factoring, we have to take each factor, set it equal to zero, and solve to find our solutions as follows:

• x+4 = 0 → x = -4

• x+2 = 0 → x = -2

Figure 07: The final step is to set each factor equal to zero and solve.

Final Answer: The quadratic equation x² + 6x + 8=0 has a solution of x={-4,-2}.

This solution should make sense since we already knew from the graphing the parabola that this particular quadratic would equal zero at x=-4 and x=-2.

Now that Example #1 is complete, you know exactly how to factor quadratic equations and how to solve quadratic equations by factoring. However, the way that you factor will vary by problem as not all trinomials are factored the same way.

Below, you will find examples for how to solve a quadratic equation by factoring for three different occasions:

• when the leading coefficient a=1 (this applies to Example #1)

• when the leading coefficient a≠1

For a more in-depth review of factoring trinomials, we highly recommend visiting our popular Step-by-Step Guide to Factoring Polynomials. Otherwise, let’s continue on to learning how to factor quadratic equations when a=1.

---

How to Factor Quadratic Equations When a=1

For this first section, we will focus on how to factor a quadratic equation with a leading coefficient of 1 (as opposed to any other number). Figure 08 highlights the difference between a quadratic equation where a=1 and a quadratic equation where a≠1.

Figure 08: Make sure that you can recognize when a quadratic has a leading coefficient of one or not.

Example #2: Factor and Solve x² -2x -15 = 0

First, note that this quadratic equation is in the form ax² + bx + c = 0 since the equation could be rewritten as:

• x² + (-2x) + (-15) =0

However, for the sake of simplicity, we will keep it as:

• x² -2x -15 =0

Since a=1 in this example, we can solve this quadratic equation the same way we solved Example #1.

First, we can split the quadratic into two parts: the left-side of the equal sign and the right-side of the equal sign. Then we can attempt to factor the trinomial x² -2x -15 on the left-side.

Figure 09: How to Factor Quadratic Equations: Start by isolating the trinomial on the left-side of the equal sign.

Now, we can find the factors of x² -2x -15 as follows:

Step One: Identify the values of b and c.

In this example, the values of b and c are: b=-2 & c=-15

Step Two: Find two numbers that both ADD to b and MULTIPLY to c.

Once you have identified the values of b and c (-2 and -15 respectively in this example), you can use trial-and-error to find two numbers that both add to the b term (-2) and multiply to the c term (-15). Another way to say this is: find two numbers with a sum of -2 and a product of -15.

In cases like this example, you need two number that will multiply to a -15. Since the product of two negatives is always positive and the product of two positives is also always positive, your factors will include one positive number and one negative number.

After some trial-and-error, you will find that 3 and -5 work because:

• 3 + -5 = -2 (the value of b) ✓

• 3 x -5 = -15 (the value of c) ✓

Since the sum of 3 and -5 is -2 and the product of 3 and -5 is -15, you have found out that the factors of the trinomial x² -2x -15 are (x+3) and (x-5)

Step Three: Use your numbers from step two to write out the factors

In this case, you can conclude that the factors of x² -2x -15 are (x+3) and (x-5).

Figure 10: Factor the trinomial on the left-side of the equal sign.

From here, we have a new equation to deal with:

• (x+3)(x-5)=0

To find the solution(s) to the original quadratic equation, we have to take each factor, set it equal to zero, and solve for x as follows:

• x+3 = 0 → x = -3

• x-5 = 0 → x = 5

Figure 11: How to Solve a Quadratic Equation by Factoring

Final Answer: The quadratic equation x² - 2x - 15 =0 has a solution of x={-3,5}.

Now, let’s look at one more example of how to factor quadratic equations when the leading coefficient is 1.

---

Example #3: Factor and Solve x² + 4x = 12

Do you notice anything different about this next example?

The equation is not a quadratic (i.e. it is not in ax² +bx + c = 0 form). To get this equation into ax² +bx + c = 0, we will have to rearrange it, namely by subtracting 12 from both sides so that there is a zero on the right side of the equals sign as follows:

• x² + 4x = 12

• x² + 4x -12 = 12 -12

• x² + 4x -12 = 0

By rearranging the terms in this way, our new equation is a quadratic that is now in ax² +bx + c = 0 form, meaning that we can solve it by factoring.

Figure 12: How to Factor a Quadratic Equation

Now, we can find the factors of x² +4x -12 as follows:

Step One: Identify the values of b and c.

In this example, the values of b and c are: b=4 & c=-12

Step Two: Find two numbers that both ADD to b and MULTIPLY to c.

Once you have identified the values of b and c (4 and -12 respectively in this example), you can use trial-and-error to find two numbers that both add to the b term (4) and multiply to the c term (-12). Another way to say this is: find two numbers with a sum of 4 and a product of -12.

After some trial-and-error, you will find that 6 and -2 work because:

• 6 + —2 = 4 (the value of b) ✓

• 6 x —2 = -12 (the value of c) ✓

Step Three: Use your numbers from step two to write out the factors

In this case, you can conclude that the factors of x² + 4x -12 are (x+6) and (x-2).

Finally, we can find our solutions by solving

• (x+6)(x-2)=0

To find the solution(s) to the original quadratic equation, we have to take each factor, set it equal to zero, and solve for x as follows:

• x+6 = 0 → x = -6

• x-2 = 0 → x = 2

Final Answer: The quadratic equation x² + 4x - 12 = 0 has a solution of x={-6,2}.

The entire step-by-step process for solving this example is illustrated in Figure 12 above. Now let’s move onto learning bow to factor a quadratic equation when the leading coefficient is not equal to one.

---

How to Factor Quadratic Equations When a≠1

Example #4: Factor and Solve 2x² - x - 6 = 0

For the first example, we have to find the solutions to the quadratic equation: 2x² - x - 6 = 0.

Notice that, in this case, the leading coefficient a≠1 (in this example a=2).

We can still solve this quadratic equation by separating the left and right-side of the equal sign where the trinomial is on the left side and the zero is on the right side as shown in Figure 13 below.

Figure 13: How to Factor a Quadratic Equation when a≠1

Now, we have to find the factors of the trinomial 2x² - x - 6 on the left-side of the equal sign as follows:

Figure 14: How to factor a trinomial a≠1

Factoring these types of trinomials is a bit more involved.

First, notice that you can not pull out a greatest common factor (GCF). When this is the case, you can use the AC method for factoring trinomials of the form ax² + bx + c when a≠1 as follows:

Step One: Identify the values of a and c and multiply them together

For this example, a=2 and c=-6…

• a x c = 2 x -6 = -12

Step Two: Factor and replace the middle term

Next, you have to take the resulting product from Step One (-12) and use it as a replacement for the middle term.

This means that you are replacing the middle term, -1x, with -12x, which we then have to factor as follows:

• -12 = -4 x 3; and

• -4 + 3 = -1

We chose -4 and 3 as factors because the sum of -4 and 3 equals negative 1, so we can rewrite the original trinomial as 2x² - 4x +3x - 6, as shown in Figure 15 below.

Figure 15: How to use the AC method to factor

Step Three: Split the new polynomial down the middle and take the GCF of each side

Our new polynomial is equivalent to the one that we started with, but now it has four terms: 2x² - 4x + 3x - 6

Now, you must split the polynomial down the middle to essentially create two separate binomials that you can simplify by dividing GCF’s out of as follows:

• First Binomial: 2x² - 4x = 2x(x-2)

• Second Binomial: 3x - 6 = 3(x-2)

This process of splitting the polynomial down the middle is illustrated in Figure 16 below.

Figure 16: Split the new polynomial down the middle and take the GCF of each side

Step Four: Identify the Factors

Lastly, you can now determine the factors.

The result from the previous step was 2x(x - 2) + 3(x -2). Within this expression you will find your two factors, (2x+3) and (x-2), as shown in Figure 17 below.

Figure 17: How to Factor Quadratic Equations

And now, you can conclude that the factors of 2x² - x - 6 are (2x+3) and (x-2).

Unfortunately, you still have to set these factors equal to zero and solve for x to find the solution to the original quadratic equation as follows:

• 2x + 3 = 0 → 2x = -3 → x = -3/2

• x-2 = 0 → x = 2

Final Answer: The quadratic equation 2x² - x - 6 = 0 has a solution of x={ -3/2 , 2 }.

The complete step-by-step process for solving this final example is illustrated in Figure 18 below.

Figure 18: How to Factorize Quadratic Equations

---

Conclusion: How to Solve Quadratic Equations by Factoring

Learning how to factor quadratic equations is a key algebra skill that can be learned with practice.

While many students will initially learn how to solve quadratic equations by graphing, the next step will be to learn how to solve quadratic equations by factoring, which means that you will have to know how to factor quadratic of the form ax² + bx + c = 0 when a=1 and when a≠1.

In this step-by-step guide to factoring quadratic equations, we covered both cases as we worked through several examples of factoring quadratics of the form ax² + bx + c = 0. Remember that not all questions will be directly in this form, but they can often be rearranged (i.e. they can be rewritten as an equivalent equation that is in the form ax² + bx + c = 0).

If you are still confused about how to factor quadratic equations, we highly recommend that you go back and work through all of the example problems above, carefully following each step. The more experience that you have working on these types of problems, the easier they will become.

Keep Learning:

How to Factor Polynomials (Free Step-by-Step Guide)

Learn how to factor binomials, trinomials, and cubic expressions.

---

How to Simplify Fractions in 3 Easy Steps

How to Simplify Fractions in 3 Easy Steps

Math Skills: How to simplify fractions, How to simplify a fraction by finding a greatest common factor

Learn How to Simplify Fractions in 3 Easy Steps

One of the most important math skills related to fractions is understanding how to simplify fractions.

While simplifying fractions can seem tricky at first, it is a math skill that most math students can master with a good amount of practice combined with a strong conceptual and procedural understanding of fractions.

This free Step-by-Step Guide on How to Simplify Fractions will teach you everything you need to know about simplifying fractions, including proper fractions, improper fractions, and mixed fractions. Together, we will use a simple 3-step process for simplifying fractions that you can use to solve any problem where you have to simplify a fraction!

You can use the quick-links below to jump to any section of this guide, or you can continue on and follow it step-by-step:

• Fraction Review and Key Vocabulary

• What Does it Mean to Simplify a Fraction?

• How to Simplify Fractions in 3 Easy Steps

Before we start working on any practice problems, let’s do a quick review of some important math vocabulary terms related to fractions that you will need to understand well to make the most out of this guide.

Fractions Review: Definitions and Vocabulary

Before you learn how to simplify fractions, it’s important that you have a strong foundational understanding of what fractions are in general.

For starters, let’s review the difference between the numerator of a fraction and the denominator of a fraction. The numerator of a fraction is the top number and the denominator of a fraction is the bottom number. For example, the fraction 3/5 has a numerator of 3 and a denominator of 5.

In this guide, whenever we reference the numerator of a fraction, we are talking about the top number. Conversely, whenever we reference the denominator of a fraction, we are talking about the bottom number.

Figure 01: The fraction 3/5 has a numerator of 3 and a denominator of 5

Next, let’s recap the difference between the three types of fractions:

• Proper Fractions

• Improper Fractions

• Mixed Fractions

Proper Fractions

Definition: A proper fraction is a fraction with a numerator that is smaller than the denominator. For example, 3/8 is a proper fraction because 3 < 8. The value of a proper fraction is always less than one whole.

• Examples: 3/8, 1/2, 7/9

Improper Fractions

Definition: An improper fraction is a fraction with a numerator that is greater than the denominator. For example, 7/5 is a proper fraction because 7 > 5. The value of an improper fraction is always greater than one whole.

• Examples: 5/2, 12/11, 9/4

Mixed Fractions

Definition: A mixed fraction is a fraction that is a combination, or sum, of a whole number and a proper fraction. For example, 4 1/2 is a mixed fraction that represents the sum of 4 and 1/2.

• Examples: 3 1/3, 7 5/8, 2 3/4

Figure 02 below illustrates examples of these three types of fractions.

Figure 02: What is the difference between a proper fraction, an improper fraction, and a mixed fraction?

Note that this guide will only focus on teaching you how to simplify a fraction that is proper.

---

What Does it Mean to Simplify a Fraction?

When we refer to simplifying fractions, we are talking about taking a fraction and reducing it down to its simplest form.

Note that not all fractions can be simplified. If the numerator and the denominator of a fraction have no common factors other than 1, then the fraction is already in simplest form and, thus, can’t be simplified. Whenever we have to simplify a fraction, you are trying to reduce it down to the point where it can no longer be simplified.

The act of simplifying a given fraction down to its most reduced form the is main objective of this guide. Whenever we simplify a fraction, we are not changing the value of the fraction. Rather, we are rewriting a new equivalent fraction that is in its simplest form (i.e. he numerator and the denominator of a fraction have no common factors other than 1).

Does this sound confusing? If so, a simple example may help. Let’s consider the fractions 1/2 and 3/6.

Figure 03: The fractions 3/6 and 1/2 are equivalent.

Figure 03 above compares the fractions 1/2 (one-half) and 3/6 (three-sixths).

We should already know that 1/2 and 3/6 are equivalent since each represent one half (i.e. one is half of two and three is half of six).

Simplifying fractions means reducing the fraction to its most reduced form whenever possible.

We can say that a fraction is in its simplest form if both the numerator and the denominator have no common factors other than 1. This is the case for 1/2, since 1 and 2 do not have any common factors other than 1, meaning that 1/2 is in its lowest possible form and it’s the simplest way of expressing one half.

But what about 3/6? Let’s consider the factors of the numerator 3 and the denominator 6:

• Factors of 3: 1, 3

• Factors of 6: 1, 2, 3, 6

Both 3 and 6 share a common factor of 3. So, if we can divide both the numerator and the denominator by 3 to find a new equivalent fraction that is in simplified form (which we already know should be 1/2). Let’s go ahead and do the math to see if our result checks out:

• 3/6 → (3 ÷ 3) / (6 ÷ 3) = 1/2

As expected, our result is 1/2. This way of mathematically proving that 3/6 and 1/2 are equivalent fractions and that 1/2 is the most simplified form of 3/6 is illustrated in Figure 04 below. The strategy that we used will serve as the basis for the 3-step method for simplifying fractions that you will learn in the next section.

Figure 04: The simplest form of a fraction is equivalent to the original fraction.

Before moving on, the key takeaway here is that any fraction in simplest form will be equivalent to whatever fraction you started with. However, this new simplified fraction is in its lowest form and can not be simplified further. For example, 3/5 is in simplest form because 3 and 5 do not share a greatest common factor other than 1.

Now let’s move onto working through some sample problems using a simple 3-step process for how to simplify fractions.

---

How to Simplify Fractions (Proper Fractions)

Example #1: Simplify: 8/32

To solve this first example as well as any problem where you have to simplify a fraction, we will use the following 3-step method for simplifying fractions:

1. Step One: List the factors of both the numerator and the denominator

2. Step Two: Determine the value of the greatest common factor shared by both the numerator and the denominator

3. Step Three: Divide both the numerator and the denominator by the greatest common factor to find a new equivalent fraction that is in simplest form.

Let’s go ahead and apply these three steps to the fraction 8/32 as follows:

Step One: List the factors of both the numerator and the denominator.

For this first step, we will list out all of the factors of 8 (the numerator) and 32 (the denominator) as follows:

• Factors of 8: 1, 2, 4, 8

• Factors of 32: 1, 2, 4, 8, 16, 32

Step Two: Determine the value of the greatest common factor shared by both the numerator and the denominator

Notice that 8 and 32 have three shared common factors: 2, 4, and 8. However, the greatest common factor shared by 8 and 32 is 8.

• The greatest common factor shared by 8 and 32 is 8.

Figure 05: 8 and 32 share a greatest common factor of 8

Step Three: Divide both the numerator and the denominator by the greatest common factor to find a new equivalent fraction that is in simplest form.

For the final step, we have to divide both the numerator and the denominator by 8 as follows:

• 8/32 → (8 ÷ 8) / (32 ÷ 8) = 1/4

Our result, 1/4 is in simplest form because both 1 and 4 do not share any factors other than 1, so we can conclude that:

Final Answer: The fraction 8/32 can be simplified to 1/4.

That’s all there is to it! Go ahead and review the Example #1 recap shown in Figure 06 below before moving onto the next example.

Figure 06: How to Simplify Fractions in 3 Easy Steps.

---

How to Simplify a Fraction Example #2: Simplify: 18/27

Just like the previous example, we will again use our 3-step method to simplify the fraction 18/27 as follows:

Step One: List the factors of both the numerator and the denominator.

First, let’s list all of the factors of 18 and 27:

• Factors of 18: 1, 2, 3, 6, 9, 18

• Factors of 27: 1, 3, 9, 27

Step Two: Determine the value of the greatest common factor shared by both the numerator and the denominator

In this case, 18 and 27 share a greatest common factor of 9.

Figure 07: How to Simplify a Fraction: Start by finding the greatest common factor shared by the numerator and the denominator.

Step Three: Divide both the numerator and the denominator by the greatest common factor to find a new equivalent fraction that is in simplest form.

Finally, the last step is to divide both the numerator and the denominator by 9:

• 18/27 → (18 ÷ 9) / (27 ÷ 9) = 2/3

The resulting fraction, 2/3, is in simplest form because both 2 and 3 do not share any factors other than 1.

Final Answer: The fraction 18/27 can be simplified to 2/3.

Our entire approach to solving Example #2 is recapped in Figure 08 below.

Figure 08: How to Simplify a Fraction

Now, let’s work through one more example of how to simplify a fraction that is proper.

---

How to Simplify Fractions Example #3: Simplify: 66/93

We can simplify 66/93 using our 3-step process as follows:

Step One: List the factors of both the numerator and the denominator.

Start by listing all of the factors of 66 and 93:

• Factors of 66: 1, 2, 3, 6, 11, 22, 33, 66

• Factors of 93: 1, 3, 31, 93

Step Two: Determine the value of the greatest common factor shared by both the numerator and the denominator

Now that all of the factors are listed, we can see that 66 and 93 share a greatest common factor of 3.

Figure 09: 66 and 93 share a greatest common factor of 3.

Step Three: Divide both the numerator and the denominator by the greatest common factor to find a new equivalent fraction that is in simplest form.

For the final step, we have to divide both the numerator and the denominator by 3:

• 66/93 → (66 ÷ 3) / (93 ÷ 3) = 22/31

The result, 22/31, is in simplest form because both 22 and 31 do not share any factors other than 1.

Final Answer: The fraction 66/93 can be simplified to 22/31.

Figure 10: How to simplify a fraction by finding a greatest common factor.

---

Conclusion: How to Simplify Fractions

Whenever you have to simplify a fraction, you have to reduce the fraction down to its simplest form, meaning that the new fraction’s numerator and denominator have no common factors besides 1.

When you simplify a fraction, you are finding a new reduced form fraction that is equivalent to the original fraction. For example, 3/6 can be simplified as 1/2 and both are equivalent to “one half".”

You can solve any problem where you have to simplify a fraction by following this easy 3-step method:

How to Simplify Fractions in 3 Easy Steps

1. Step One: List the factors of both the numerator and the denominator

2. Step Two: Determine the value of the greatest common factor shared by both the numerator and the denominator

3. Step Three: Divide both the numerator and the denominator by the greatest common factor to find a new equivalent fraction that is in simplest form.

To gain some more practice using these steps, we recommend that you go back and work through the practice problems in this guide on your own a second time or to work on some of the free Simplifying Fractions Worksheets available on our math worksheet libraries page.

Keep Learning:

How to Subtract Fractions in 3 Easy Steps (free Step-by-Step Guide for Students)

---

Search Tags: how to add fractions, how to add fractions with different denominators, how to add fraction , how to add fractions with unlike denominators, how to. add fractions, how to add fractions with, how to add a fraction