Factors of 30
What are all of the factors of 30? What is the prime factorization of 30?
eFactors of 30
What are all of the factors of 30? What is the prime factorization of 30?
What are the factors of 30?
If a whole number can be divided into 30 without leaving a remainder, it is considered one of the factors of 30.
If you're just looking for a quick answer to the question what are the factors of 30?, you can find them below. However, if you are interested in a more detailed explanation on how to find all the factors of 30 (or any other number), keep reading! We've got a step-by-step guide that will even show you how to find the prime factorization of 30.
▶ Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
▶ Prime Factorization of 27: 2 x 3 x 5
What are the factors of 30?
In math, the term factor refers to any number that can be divided evenly into another number without a remainder.
For example:
8 is a factor of 16 because 16 ÷ 8 = 2 → There isn’t a remainder.
10 is not a factor of 16 because 16 ÷ 10 = 1.6 → Because the result is a decimal, there is a remainder.
Whenever you need to figure out the factors of a number, you'll be using division to create a list of factors. The trick is to find numbers that divide into 30 (or whatever number you are factoring) and give you a whole number as the result (no decimals or remainders). Any number that meets these requirements (dividing into 30 evenly without a remainder) will be on of the factors of 30.
The process of figuring out the complete list of factors of any number (30 in this case) is illustrated in Figure 01 below.
Figure 01: What is a factor of 30?
What is a factor of 30? Let’s take a look at two examples: the first example is a factor of 30 and the second example is not a factor of 30.
3 is a factor of 30 because 30 ÷ 3 = 10 → There isn’t a remainder.
7 is not a factor of 30 because 30 ÷ 7 = 4.29 → Because the result is a decimal, there is a remainder.
What are all of the factors of 30?
In a nutshell, the process of finding all the factors of 30 (or any number, really), all you need to do is use division to see which whole numbers can divide into 30 without leaving any remainder (no decimals).
The easiest way to find all the factors of 30 is to start by dividing it by 1 and then move on to 2, 3, 4, 5, 6, and so on. Any number that divides into 30 without leaving a remainders is a factor of 30.
*The number 1 is a factor of every number because it can divide into any number without leaving a remainder (since any whole number divided by 1 is equal to itself). So, you can always include 1 on the list of factors for any number.
**Also, the number itself is always a factor because any whole number divided by itself equals 1, which is a whole number without a remainder. So, you can always include the number itself on the list of factors for any number.
At this point, you already know two of the factors of 30 are 1 and 30.
Now, you can find the rest of the factors of 30 using the previously described process of using division. Figure 02 below walks you through checking whether or not the numbers one through ten are factors of 30 or not.
Figure 02: What are the factors of 30?
After working through the table, it is clear that the whole numbers between 1 and 10 that can be divided evenly into 30 without a remainder are 1, 2, 3, 5, 6, and 10, so all of these numbers will be on the list of factors of 30.
By continuing this same process with numbers beyond 10, you will find two more factors of 30:
15 is a factor of 30 because 30 ÷ 15 = 2 → the result is a whole number with no reminder
30 is a factor of 30 because 30 ÷ 30 = 1 → the result is a whole number with no remainder
So, you can conclude that all of the factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30
Figure 03: The factors of 30 are 1,2,3,5,6,10,15,30
Prime Factorization of 30
Now that we know all of the factors of 30, we can move onto figuring out the prime factorization of 30.
When we talk about prime factorization in math, we're essentially trying to find the prime numbers that can be multiplied together to result in whatever number you started with. So, to find the prime factorization of 30, we need to express 30 as the product of its prime factors.
It is important to note that prime factors are numbers that are factors of 30 AND also prime numbers.
Figure 04 below is a complete list of all of the prime numbers up to 50 for your reference.
View fullsize
Figure 04: Prime Factorization of 30 What is the factorization of 30?
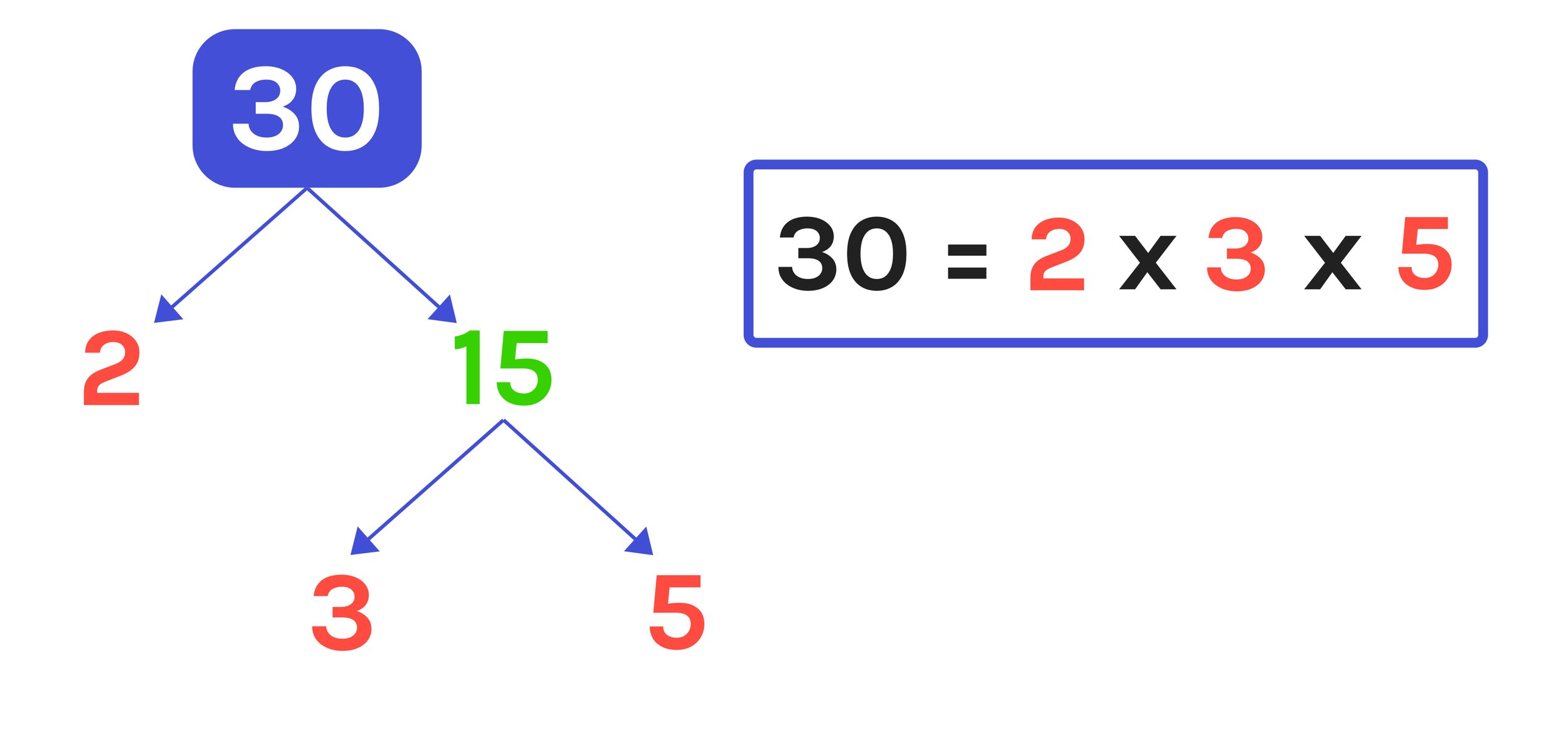
An easy way to figure out the prime factorization of 30 is to use a factor tree that shows the prime factors of 30.
The factor tree of the prime factorization of 30 is shown in Figure 05 below.
Figure 05: Factorization of 30: The prime factorization of 30=2x3x5
Now we can make the conclusion that the prime factorization of 30 is:
30 = 2 x 3 x 5
We've just figured out all the factors of 30 as well as the prime factorization of 30. If you understand this process, you can use the same steps to find the factors and prime factorization of any other number! But, if you're still feeling unsure about the factoring process, we recommend going back through the examples in this guide to gain some more experience.
Keep Learning:
The Ultimate Guide to Passing the Texas STAAR Test
5 Awesome Math Teacher Gift Ideas
How to Subtract Fractions with Different Denominators (Step-by-Step)
Why Every Teacher Should Say "No" More Often
How to Add Fractions with Different Denominators (Step-by-Step)
Are Timed Math Tests Harmful to Students?
How to Simplify Radicals in 3 Easy Steps
Free Printable Math Puzzles for Middle School Students
How to Factor Quadratic Equations—Step-by-Step Examples and Tutorial
Search Tags: factors of 30, prime factorization of 30, what are the factors of 30, what is a factor of 30, what is the factorization of 30, factor of 30, what is the prime factorization of 30, all factors of 30, prime factors of 30, what are the prime factorization of 30, what are the factors of 30
Mashup Math
More Info
Terms of Use
© 2023 Mashup Math LLC. All rights reserved.
DO NOT SELL OR SHARE MY INFORMATIONIf a whole number can be divided into 30 without leaving a remainder, it is considered one of the factors of 30.
If you're just looking for a quick answer to the question what are the factors of 30?, you can find them below. However, if you are interested in a more detailed explanation on how to find all the factors of 30 (or any other number), keep reading! We've got a step-by-step guide that will even show you how to find the prime factorization of 30.
▶ Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
▶ Prime Factorization of 27: 2 x 3 x 5
What are the factors of 30?
In math, the term factor refers to any number that can be divided evenly into another number without a remainder.
For example:
8 is a factor of 16 because 16 ÷ 8 = 2 → There isn’t a remainder.
10 is not a factor of 16 because 16 ÷ 10 = 1.6 → Because the result is a decimal, there is a remainder.
Whenever you need to figure out the factors of a number, you'll be using division to create a list of factors. The trick is to find numbers that divide into 30 (or whatever number you are factoring) and give you a whole number as the result (no decimals or remainders). Any number that meets these requirements (dividing into 30 evenly without a remainder) will be one of the factors of 30.
The process of figuring out the complete list of factors of any number (30 in this case) is illustrated in Figure 01 below.
Figure 01: What is a factor of 30?
What is a factor of 30? Let’s take a look at two examples: the first example is a factor of 30 and the second example is not a factor of 30.
3 is a factor of 30 because 30 ÷ 3 = 10 → There isn’t a remainder.
7 is not a factor of 30 because 30 ÷ 7 = 4.29 → Because the result is a decimal, there is a remainder.
What are all of the factors of 30?
In a nutshell, the process of finding all the factors of 30 (or any number, really), all you need to do is use division to see which whole numbers can divide into 30 without leaving any remainder (no decimals).
The easiest way to find all the factors of 30 is to start by dividing it by 1 and then move on to 2, 3, 4, 5, 6, and so on. Any number that divides evenly into 30 without leaving any remainders is a factor of 30.
*The number 1 is a factor of every number because it can divide into any number without leaving a remainder (since any whole number divided by 1 is equal to itself). So, you can always include 1 on the list of factors for any number.
**Also, the number itself is a always a factor because any whole number divided by itself equals 1, which is a whole number without a remainder. So, you can always include the number itself on the list of factors for any number.
At this point, you already know two of the factors of 30 are 1 and 30.
Now, you can find the rest of the factors of 30 using the previously described process of using division. Figure 02 below walks you through checking whether or not the numbers one through ten are factors of 30 or not.
Figure 02: What are the factors of 30?
After working through the table, it is clear that the whole numbers between 1 and 10 that can be divided evenly into 30 without a remainder are 1, 2, 3, 5, 6, and 10, so all of these numbers will be on the list of factors of 30.
By continuing this same process with numbers beyond 10, you will find two more factors of 30:
15 is a factor of 30 because 30 ÷ 15 = 2 → the result is a whole number with no reminder
30 is a factor of 30 because 30 ÷ 30 = 1 → the result is a whole number with no remainder
So, you can conclude that all of the factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30
Figure 03: The factors of 30 are 1,2,3,5,6,10,15,30
Prime Factorization of 30
Now that we know all of the factors of 30, we can move onto figuring out the prime factorization of 30.
When we talk about prime factorization in math, we're essentially trying to find the prime numbers that can be multiplied together to result in whatever number you started with. So, to find the prime factorization of 30, we need to express 30 as the product of its prime factors.
It is important to note that prime factors are numbers that are factors of 30 AND also prime numbers.
Figure 04 below is a complete list of all of the prime numbers up to 50 for your reference.
Figure 04: Prime Factorization of 30 What is the factorization of 30?
An easy way to figure out the prime factorization of 30 is to use a factor tree that shows the prime factors of 30.
The factor tree of the prime factorization of 30 is shown in Figure 05 below.
Figure 05: Factorization of 30: The prime factorization of 30=2x3x5
Now we can make the conclusion that the prime factorization of 30 is:
30 = 2 x 3 x 5
We've just figured out all the factors of 30 as well as the prime factorization of 30. If you understand this process, you can use the same steps to find the factors and prime factorization of any other number! But, if you're still feeling unsure about the factoring process, we recommend going back through the examples in this guide to gain some more experience.
Keep Learning:
Search Tags: factors of 30, prime factorization of 30, what are the factors of 30, what is a factor of 30, what is the factorization of 30, factor of 30, what is the prime factorization of 30, all factors of 30, prime factors of 30, what are the prime factorization of 30, what are the factors of 30