How to Find the Area of a Parallelogram
Math Guide: How to Find the Area of a Parallelogram in 3 Easy Steps
Step-by-Step Guide: How to find the area of a parallelogram.
When studying geometric figures in math, you will eventually learn about parallelograms. By definition, a parallelogram is a quadrilateral (a four-sided figure) with two pairs of sides that are parallel to each other (hence the name parallelogram).
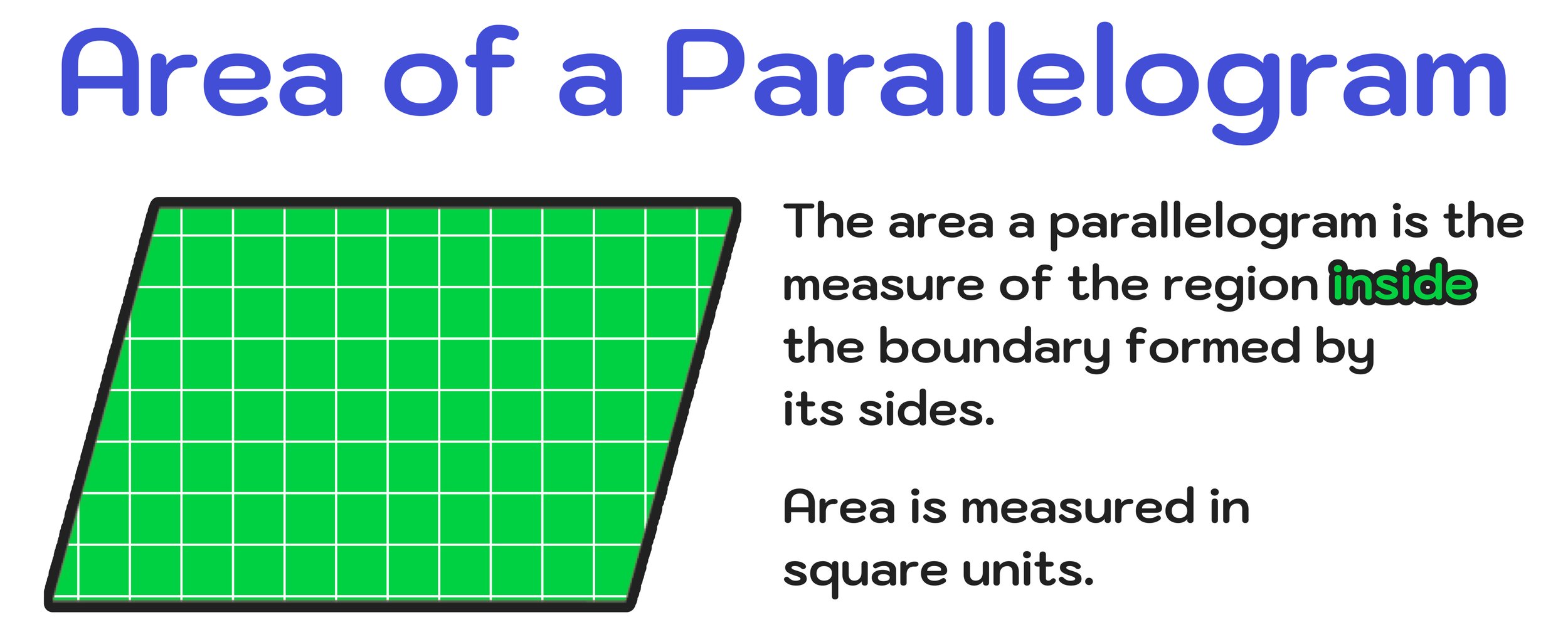
What is the area of a parallelogram? The area of a parallelogram refers to the measure of the area enclosed by its four sides. The larger a parallelogram is, the larger its area will be. The area of any parallelogram is always expressed in terms of units squared (this is always the case whenever you are dealing with the area of any two-dimensional figure).
(Are you looking for a free Area of a Parallelogram Calculator? Click here to access our Area of a Parallelogram Calculator)
This step-by-step guide on how to find the area of a parallelogram covers the following topics:
What is the Area of a Parallelogram?
Figure 01: What is the area of a parallelogram?
What is the area of a parallelogram? The area of a parallelogram is the measure of the space contained by its four sides. To find the area of a parallelogram, you can think of it like a rectangle that has been slightly skewed to one side so that the angle measures are no longer equal to 90 degrees. Therefore, the area of a parallelogram can be found the same way that you would find the area of a rectangle.
Additionally, as previously mentioned, the area of a parallelogram will always be expressed using square units such as square meters, square feet, square centimeters, etc.
Calculating the area of a parallelogram can be simple as long as you know how to identify the side lengths and use the area of a parallelogram formula.
The formula for area of a parallelogram can be used whenever you have to find the area of a parallelogram of any size or orientation.
Now, let’s move onto learning about the area of a parallelogram formula and how to use it to solve problems.
What is the Area of a Parallelogram Formula?
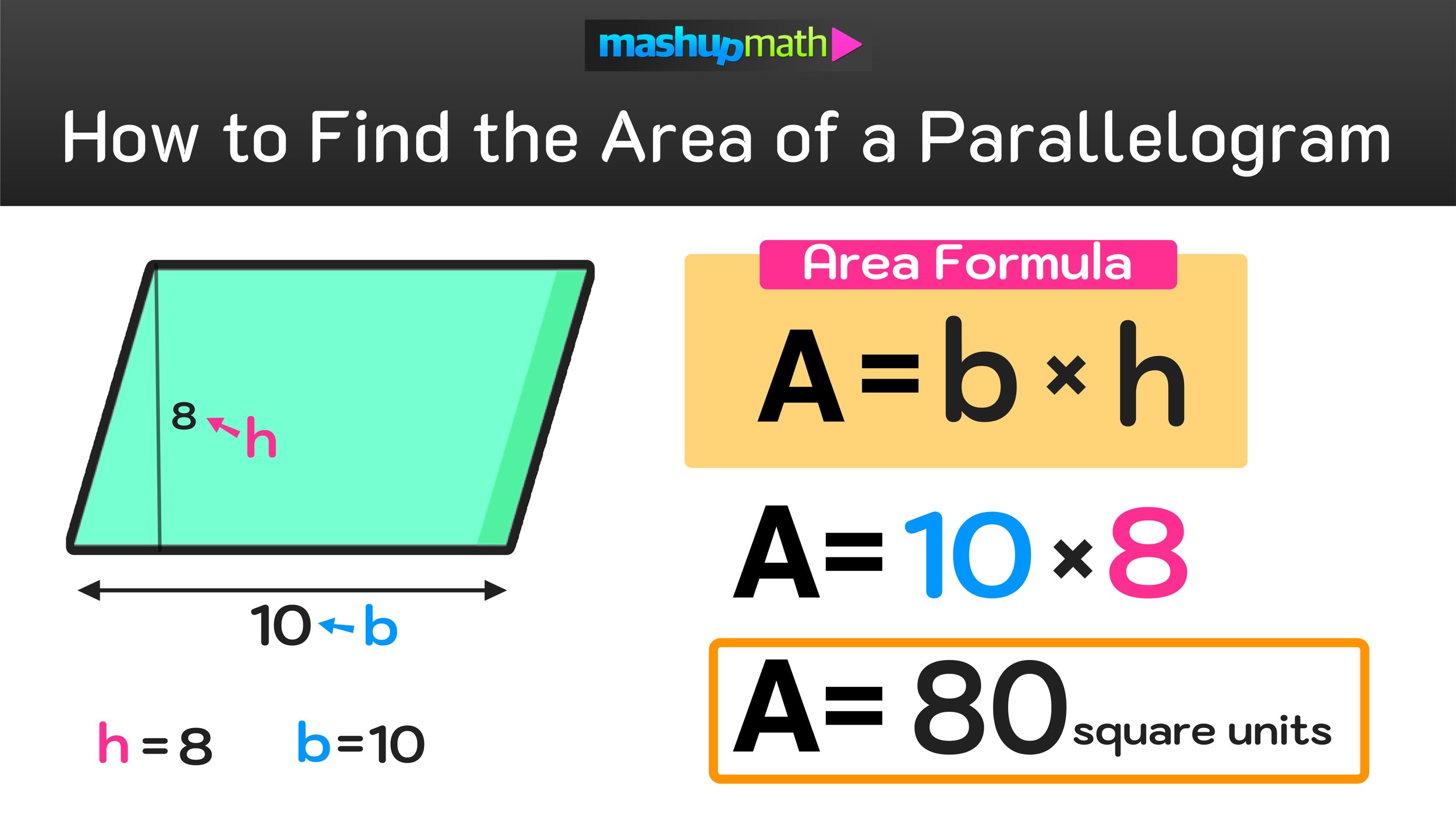
Figure 02: What is the area of a parallelogram formula? The formula for area of a parallelogram is A = b x h
You can find the area of a parallelogram with base length, b, and height, h, by using the formula for area of a parallelogram: A = b x h
How to Find the Area of a Parallelogram in 3 Easy Steps
Being able to calculate the area of a parallelogram is an important and useful math skill that you can easily learn by practicing and applying the following three steps for calculating the area of a pentagon.
The 3 steps for how to find the area of a parallelogram:
Step One: Identify the value of b (the base of the parallelogram) and h (the height of the parallelogram)
Step Two: Input the values of b and h into the area of a parallelogram formula, A = b x h, and solve for A
Step Three: Write the final answer using square units
Now, let’s look at a quick example of finding the area of a parallelogram when you know the measure of its base and the measure of its height.
In this case, the parallelogram in question has a base of 10cm and a height of 8cm (see the figure shown in Figure 03 below for more details).
Figure 03: Find the area of a parallelogram when b=10 and h=8
Step One: Identify the value of b (the base of the parallelogram) and h (the height of the parallelogram)
In this case, the measure of the base of the parallelogram is 10cm and the measure of the height of the parallelogram is 8cm, so b=10 and h=8
Step Two: Input the values of b and h into the area of a parallelogram formula, A = b x h, and solve for A
Next, substitute b=10 and h=8 into the formula for area of a parallelogram, A = b x h
A = b x h → A = 10 x 8 = 80
Step Three: Write the final answer using square units
Finally, write your final answer using square units
Final Answer: The area of the parallelogram is 80 cm^2 (or square centimeters)
Figure 04: What is the area of a parallelogram?
By learning to follow the 3-step process used to solve the previous example, you can then apply it to any future problem that involves finding the area of a parallelogram (as long as you know its base length and height).
Moving on, let’s gain some experience with using the 3 steps to find the area of a parallelogram by solving two more how to find the area of a parallelogram example problems.
How to Find the Area of a Parallelogram Examples
Example #1: Find the area of a parallelogram with a height of 14 inches and a base of 22 inches
Example #1: Find the area of a parallelogram with a height of 14 in and a height of 22 in.
Finding the area of a parallelogram when you know the length of the base and the height can be done by following the same three steps as the previous example as follows:
Step One: Identify the value of b (the base of the parallelogram) and h (the height of the parallelogram)
In this example, the parallelogram has a base of 22 inches and a height of 14 inches, so b=22 and h=14
Step Two: Input the values of b and h into the area of a parallelogram formula, A = b x h, and solve for A
For the next step, you are ready to substitute b=22 and h=14 into the formula for area of a parallelogram, A = b x h
A = b x h → A = 22 x 14 = 308
Step Three: Write the final answer using square units
Lastly, you can conclude that the area of the parallelogram is 308 square inches.
Final Answer: The area of the parallelogram is 308 in^2
Example #1 Solved: Find the area of a parallelogram
Example #2: Find the area of a parallelogram with a height of 50.5 yards and a base of 23.25 yards
Example #2: How to Find the Area of a Parallelogram
Just like the first example, finding the area of a parallelogram can be done following the same three steps:
Step One: Identify the value of b (the base of the parallelogram) and h (the height of the parallelogram)
For this next example, the parallelogram has a base of 23.25 yds and a height of 50.5 yds, so b=23.25 and h=50.5
Step Two: Input the values of b and h into the area of a parallelogram formula, A = b x h, and solve for A
Continuing on, input b=23.25 and h=50.5 into the area of a parallelogram formula, A = b x h
A = b x h → A = 23.25 x 50.5 = 1174.125
Step Three: Write the final answer using square units
To complete step 3, you just have to express the area using square units as follows:
Final Answer: The area of the parallelogram is approximately 1,174.1 square yards
Example #2 Solved: The area of an octagon with a side length of 23.7 meters is approximately 3,598.6 square meters.
Area of a Parallelogram Calculator
Use our Free Area of an Octagon Calculator to Check Your Work
Looking for a tool that you can use to rapidly calculate the area of a pentagon with a known base and height? Our free Area of a Parallelogram Calculator is an excellent tool for making quick calculations and for checking your answers.
To use the free calculator, simply input the value of s and press ENTER or DONE to calculate the octagon’s area in square units.
Click here to access our free Area of a Parallelogram Calculator.
Conclusion: How to Find the Area of a Parallelogram
You can find the area of a parallelogram when you know the measure of its base, b, and its height, h, by using the area of a parallelogram formula A = b x h, where A represents the area of the parallelogram (in square units).
To find the area of a parallelogram, you can follow the three steps below to find a solution:
Step One: Identify the value of b (the base of the parallelogram) and h (the height of the parallelogram)
Step Two: Input the values of b and h into the area of a parallelogram formula, A = b x h, and solve for A
Step Three: Write the final answer using square units
More Math Resources You Will Love:
Search Tags: area of a parallelogram, how to find the area of a parallelogram, area of a parallelogram formula, how to find area of a parallelogram, area of a parallelogram calculator, find the area of a parallelogram, what is the area of a parallelogram, how do you find the area of a parallelogram, what is the area of a parallelogram, formula for area of a parallelogram, finding the area of a parallelogram, formula for the area of a parallelogram