How to Find the Vertex of a Parabola

Your complete guide to finding the vertex of a parabola in 3 easy steps

Whenever you are working with and graphing quadratic equations (parabolas), you will have to know what is a vertex of a parabola and how to find the vertex of a parabola. This short guide will teach you everything you need to know about the vertex of a parabola and covers the following topics:

• What is the vertex of a parabola?

• What is the formula for the vertex of a parabola?

• How to find the vertex of a parabola

Before we explore finding the vertex of a parabola using 3 easy steps, lets quickly review some important information related to quadratic functions and parabolas.

What is a parabola?

A quadratic function in standard form is a function of the form: y=ax^2+bx+c or f(x)=ax^2+bx+c (note that, in this guide, f(x)= and y= are used interchangeably).

For example, for the standard form quadratic f(x)=x^2 +6x + 7, a=1, b=6, and c=7

The graph of a function is called a parabola—a plane curve that is U-shaped and symmetrical about an axis of symmetry that passes through a vertex point. Note that a parabola can open upwards (U-shaped) or open downwards (upside-down U-shaped).

Figure 01 below shows two parabolas (one that opens upwards and one that opens downwards) along with each parabola’s axis of symmetry and vertex point. After looking at the figure, it should make sense why a vertex point is often referred to as a “turning point of a parabola.”

What is the vertex of a parabola?

Definition: The vertex of a parabola is a sort of turning point where a parabola intersects with an axis of symmetry. For a parabola that opens upwards, the vertex point will be an absolute minimum point and for a parabola that opens downwards, the vertex point will be an absolute maximum point.

In simpler terms, what is the vertex of a parabola? The vertex is the point at the very bottom of the curve for parabolas that open upward or at the very top of the curve for parabolas that open downward.

Figure 02 below shows examples of three different parabolas graphed on the coordinate plane along with the vertex point labeled and the vertical axis of symmetry (dotted line) that passes through it.

Now that you understand what is the vertex of a parabola, you are ready to learn how to find vertex of a parabola using a simple 3-step method.

What is the formula for the vertex of a parabola?

The vertex of a parabola is the (x,y) coordinate point where a parabola and its axis of symmetry intersect.

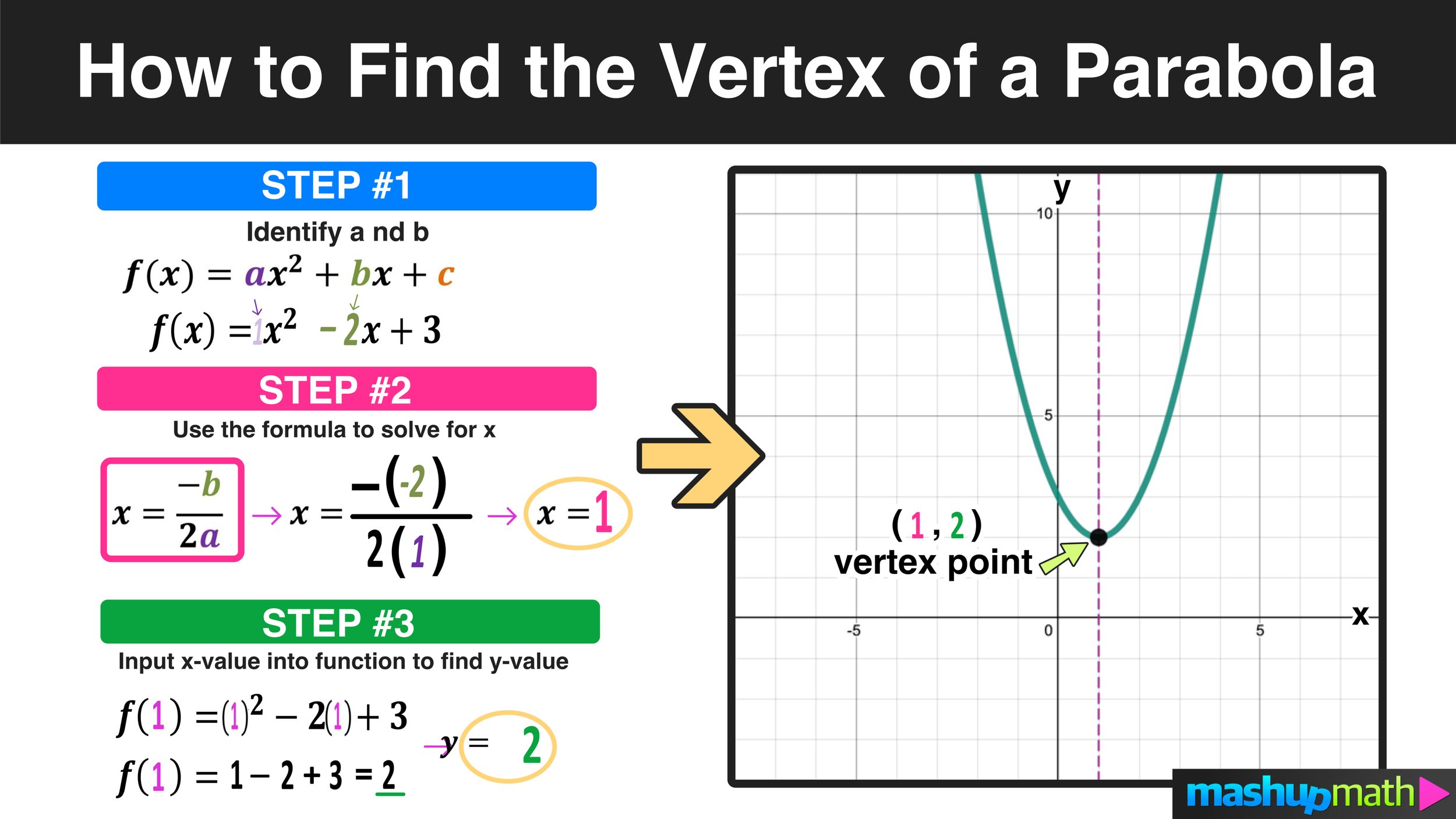
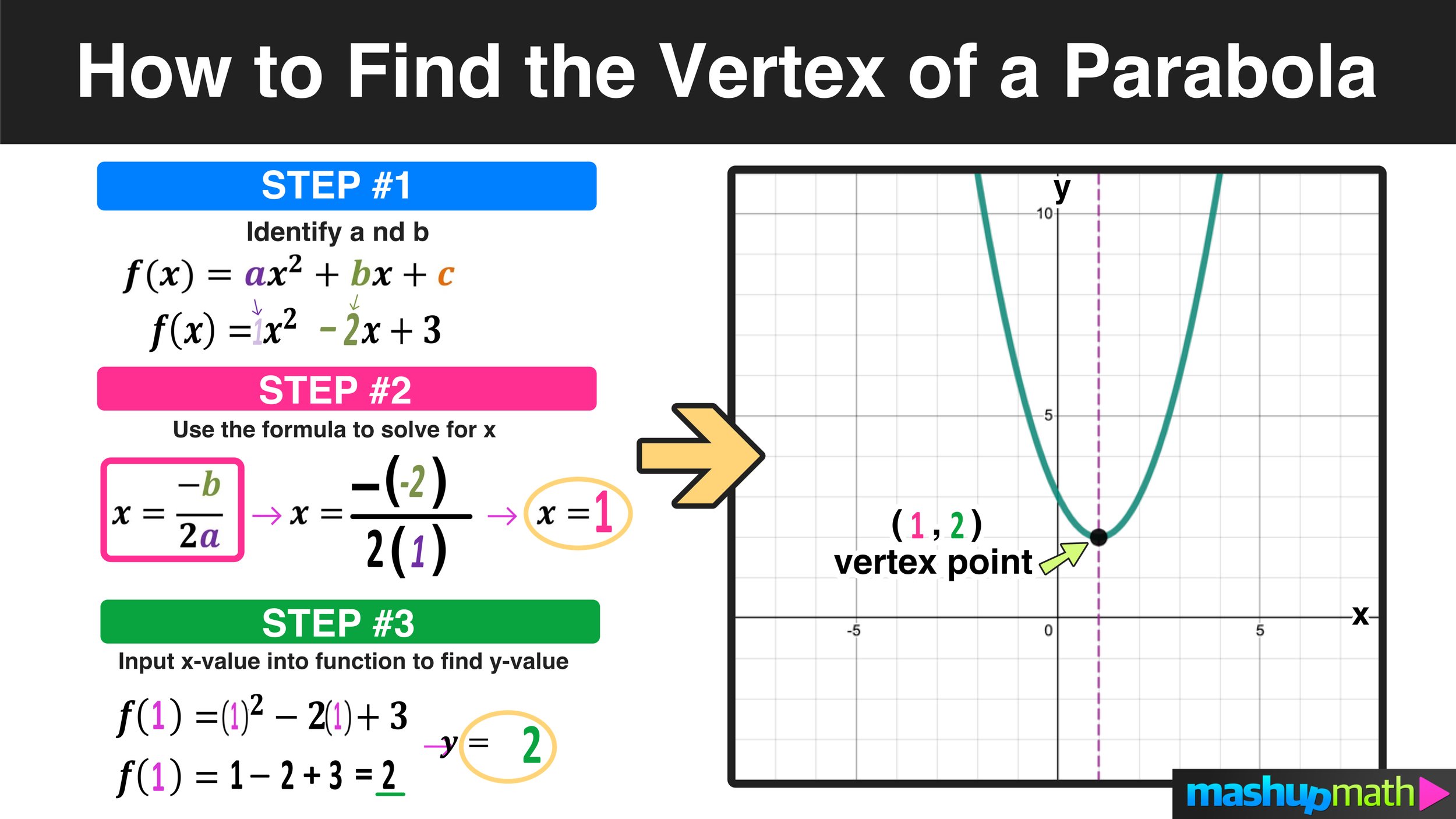
To find the vertex of a parabola represented by a quadratic function in f(x)=ax^2+bx+c form:

• Step 01: Identify the values of the coefficients a and b

• Step 02: Use the formula for the vertex of a parabola x=-b/2a to find the x-coordinate value of the vertex point.

• Step 03: Input the x-coordinate value from Step 01 into the function to find the y-coordinate value

This process, along with the vertex of a parabola formula, is summarized in Figure 03.

Moving forward, let’s gain some experience with the formula for the vertex of a parabola by working through a few examples.

How to Find the Vertex of a Parabola Example #1

Example: Find the vertex of f(x)=x^2+4x-1

Finding the vertex of a parabola with equation f(x)=x^2+4x-1 can easily be done using the 3-step process described above as follows:

Step 01: Identify the values of the coefficients a and b

Since the given quadratic function is in f(x)=ax^2+bx+c form, you can easily identify the values of a and b as:

• f(x)=x^2+4x-1 → a=1 and b=4

  (Note that a=1 because, when there is no coefficient in front of a variable, then the coefficient is 1).

Step 02: Use the formula for the vertex of a parabola x=-b/2a to find the x-coordinate value of the vertex point.

Since a=1 and b=4…

• x=-b/2a → x= -(4) / 2(1) → x =-4/2 → x = -2

Step 03: Input the x-coordinate value from Step 01 into the function to find the y-coordinate value

Now that you know that the x-coordinate value for the vertex is x=-2, you can input x=-2 into the function to find the value of the y-coordinate as follows:

• f(x)=x^2+4x-1 → f(-2) = (-2)^2 +4(-2) -1 → f(-2) = 4 - 8 -1 = -5 → y=-5

How to Find the Vertex of a Parabola Example #2

Example: Find the vertex of f(x)=-x^2+10x-9

How to find vertex of a parabola with equation f(x)=-x^2+10x-9 can be done using the same 3-step method as Example #1 as follows:

Step 01: Identify the values of the coefficients a and b

Since the given quadratic function is in f(x)=ax^2+bx+c form, you can easily identify the values of a and b as:

• f(x)=-x^2+10x-9 → a=-1 and b=10

The next step in how to find vertex of a parabola is…

Step 02: Use the formula for the vertex of a parabola x=-b/2a to find the x-coordinate value of the vertex point.

Since a=-1 and b=10

• x=-b/2a → x= -(10) / 2(-1) → x =-10/-2 → x = 5

Step 03: Input the x-coordinate value from Step 01 into the function to find the y-coordinate value

Now that you know that the x-coordinate value for the vertex is x=5, you can input x=5 into the function to find the value of the y-coordinate as follows:

• f(x)=-x^2+10x-9 → f(5) = -(5)^2 +10(5) -9 → f(5) = -25 + 50 -9 = 16 → y=16

Therefore, the coordinates of the vertex point of the parabola are (5,16). In Figure 05 below, you can see the graph of f(x)=-x^2+10x-9 on the coordinate plane with the vertex point at (5,16).

How to Find the Vertex of a Parabola Example #3

Example: Find the vertex of f(x)=3x^2-7x+3

In this final example, you will follow the same 3-steps as the previous two examples and use the vertex of a parabola formula as follows:

Step 01: Identify the values of the coefficients a and b

How do you find the vertex of a parabola with equation f(x)=3x^2-7x+3? Since the given quadratic function is in f(x)=ax^2+bx+c form, you can easily identify the values of a and b as:

• f(x)=3x^2-7x+3 → a=3 and b=-7

The next step to finding the vertex of a parabola is:

Step 02: Use the formula for the vertex of a parabola x=-b/2a to find the x-coordinate value of the vertex point.

Since a=3 and b=-7

• x=-b/2a → x= -(-7) / 2(3) → x =7/6 → x = 7/6 or x≈1.167

Step 03: Input the x-coordinate value from Step 01 into the function to find the y-coordinate value

Now that you know that the x-coordinate value for the vertex is x=1.167, you can input x=1.167 into the function to find the value of the y-coordinate as follows:

• f(x)=3x^2-7x+3 → f(1.167) = 3(1.167)^2 -7(1.167) +3 → f(1.167) ≈ -1.083 → y≈-1.083

Since finding the vertex of a parabola with equation f(x)=3x^2-7x+3 did not result in x and y-coordinate values that are integers, we will be using approximated decimal values, which is totally fine. We can conclude that the coordinates of the vertex point of the parabola are approximately (1.167,-1.083). In Figure 06 below, you can see that your approximated point is the vertex of the parabola.

How to Find Vertex of a Parabola: Conclusion

In this guide, you learned that the answer to What is the vertex of a parabola? is that the vertex is the “turning point” at the very bottom or very top of a U-shaped curved, known as a parabola, that represents a quadratic function of the form f(x)=ax^2+bx+c.

You also learned how to find the vertex of a parabola using the following 3-step process:

• Step 01: Identify the values of the coefficients a and b

• Step 02: Use the formula for the vertex of a parabola x=-b/2a to find the x-coordinate value of the vertex point.

• Step 03: Input the x-coordinate value from Step 01 into the function to find the y-coordinate value

By following this 3-step process, finding the vertex of a parabola is a relatively simple and repeatable process. Once you have mastered this skill, you are ready to learn how to graph a parabola that represents a quadratic function using our easy guide (click the link below to gain access).

More Math Resources You Will Love: