Same Side Interior Angles

Everything You Need to Know About Same Side Interior Angles

In math, same side interior angles are two angles located on the interior of (or inside) between two parallel lines that are cut by a transversal. Notably, same side interior angles are on the same side of the transversal. Additionally, the sum of any pair of same side interior angles will always equal 180 degrees.

Whenever a pair of parallel lines are intersected by a transversal, the result is a total of four interior angles. In this case, any pair of same side interior angles that are non-adjacent will have a sum of 180 degrees—meaning that they are supplementary angles.

If our initial explanation of same side interior angels sounds confusing, it will be beneficial to look at a few diagrams to better understand what same side interior angles are—since the concept is relatively easy to understand once you see what same side interior angles look like.

Furthermore, this short guide on same side interior angles will cover the following topics:

What are same side interior angles?
What is the Same Side Interior Angles Theorem?
Are same side interior angles supplementary?
Are same side interior angles congruent?

What are same side interior angles?

As described earlier, when two parallel lines are cut by a transversal, a total of 8 angles are formed. When this happens, same side interior angles are a pair of interior angles that are non-adjacent and located on the same side of the line that is the transversal.

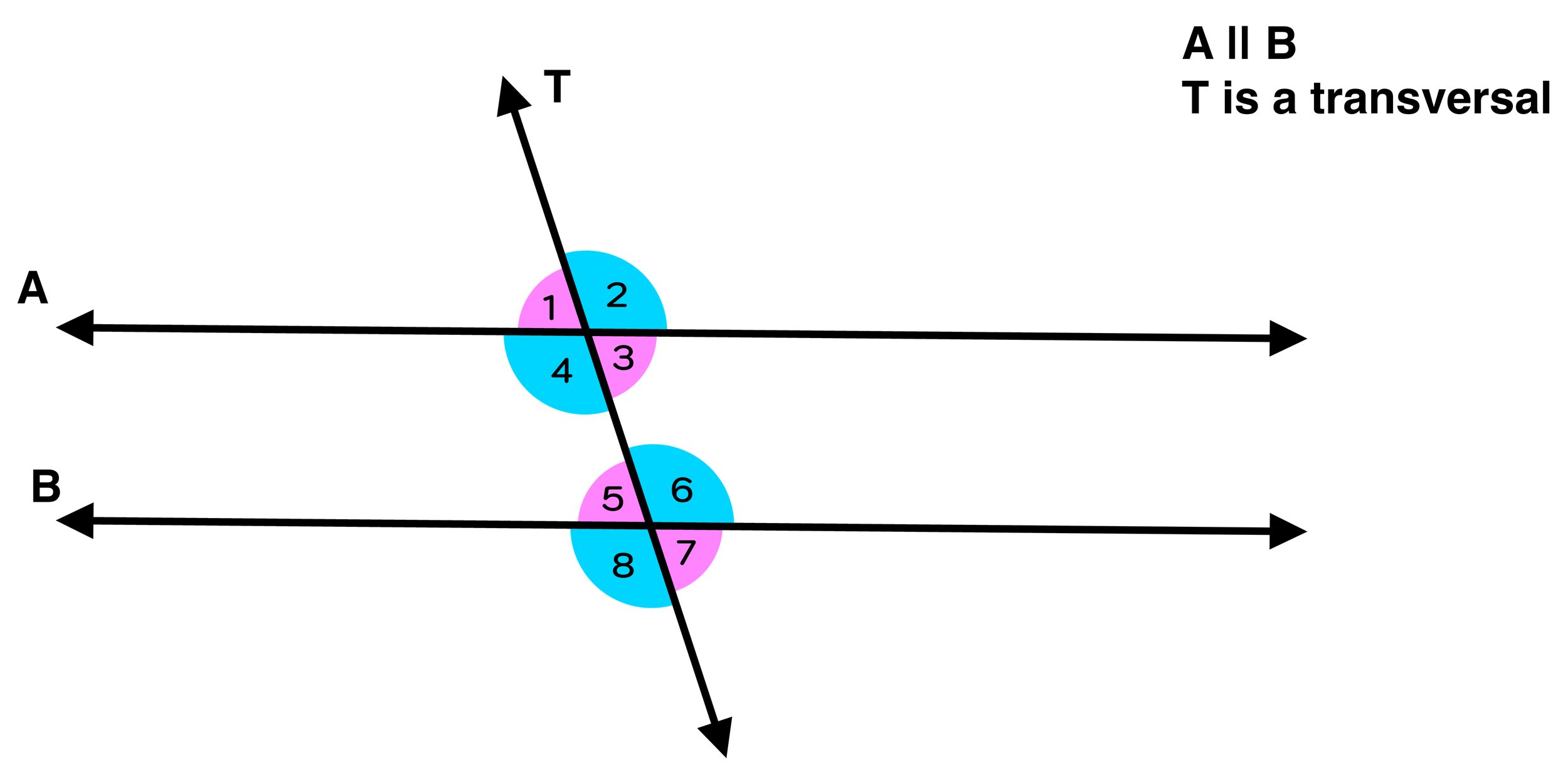
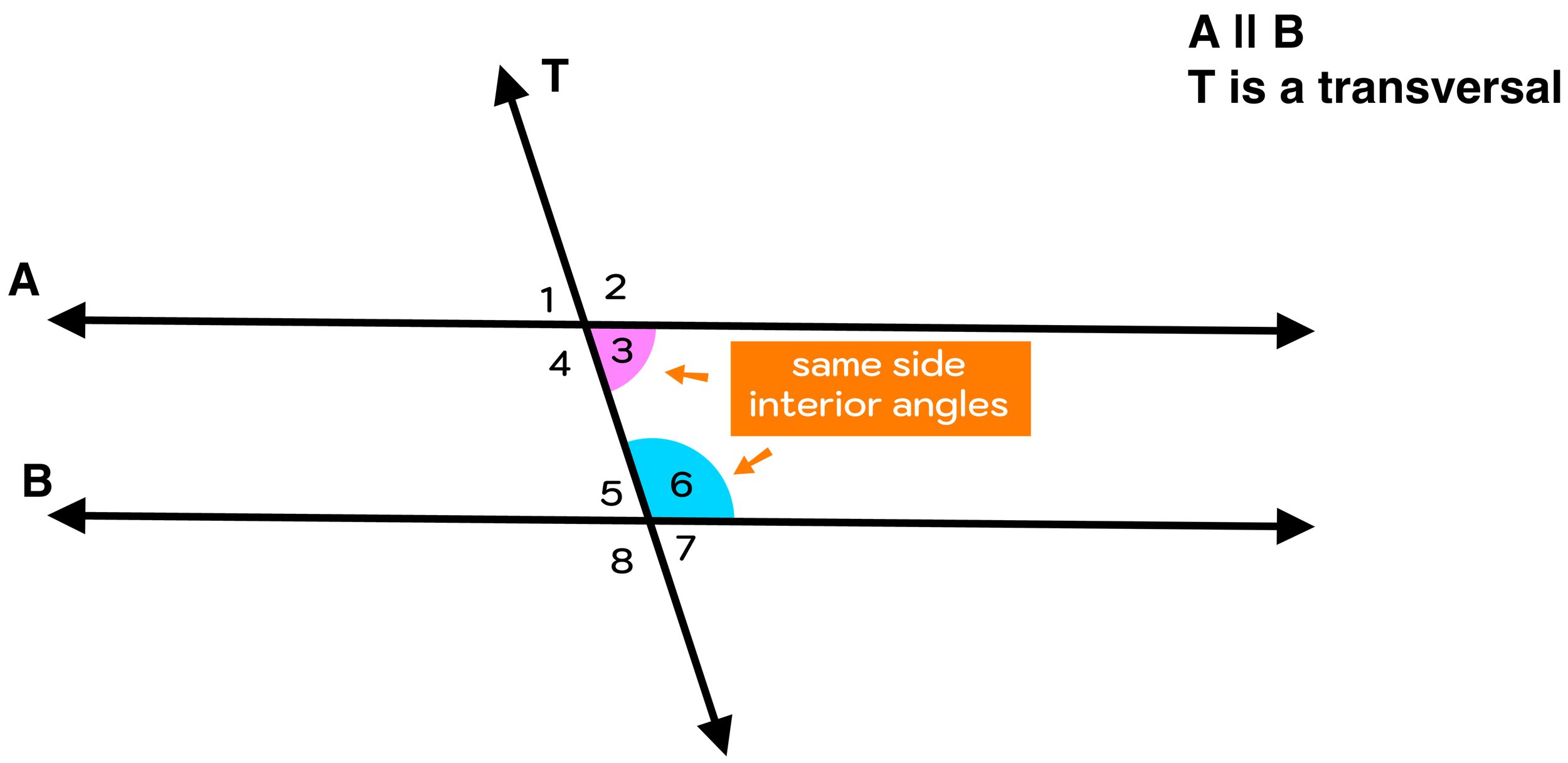
Observe Figure 01 below, where lines A and B are parallel to each other and line T is a transversal that cuts through them forming 8 angles.

For starters, let’s recap some of the properties of parallel lines cut by a transversal and the angles that they form:

All of the blue angles (∠2,∠4,∠6, and ∠8) are congruent to each other.
All of the pink angles (∠1,∠3,∠5, and ∠7) are congruent to each other.
Any combination of a blue angle and a pink angle will have a sum of 180 degrees (i.e. they form a linear pair and are supplementary).

Understanding these basic facts about parallel lines cut by a transversal is key for understanding same side interior angles. If you want a more in-depth review, check out our free video lesson on parallel lines cut by a transversal, otherwise you can continue on.

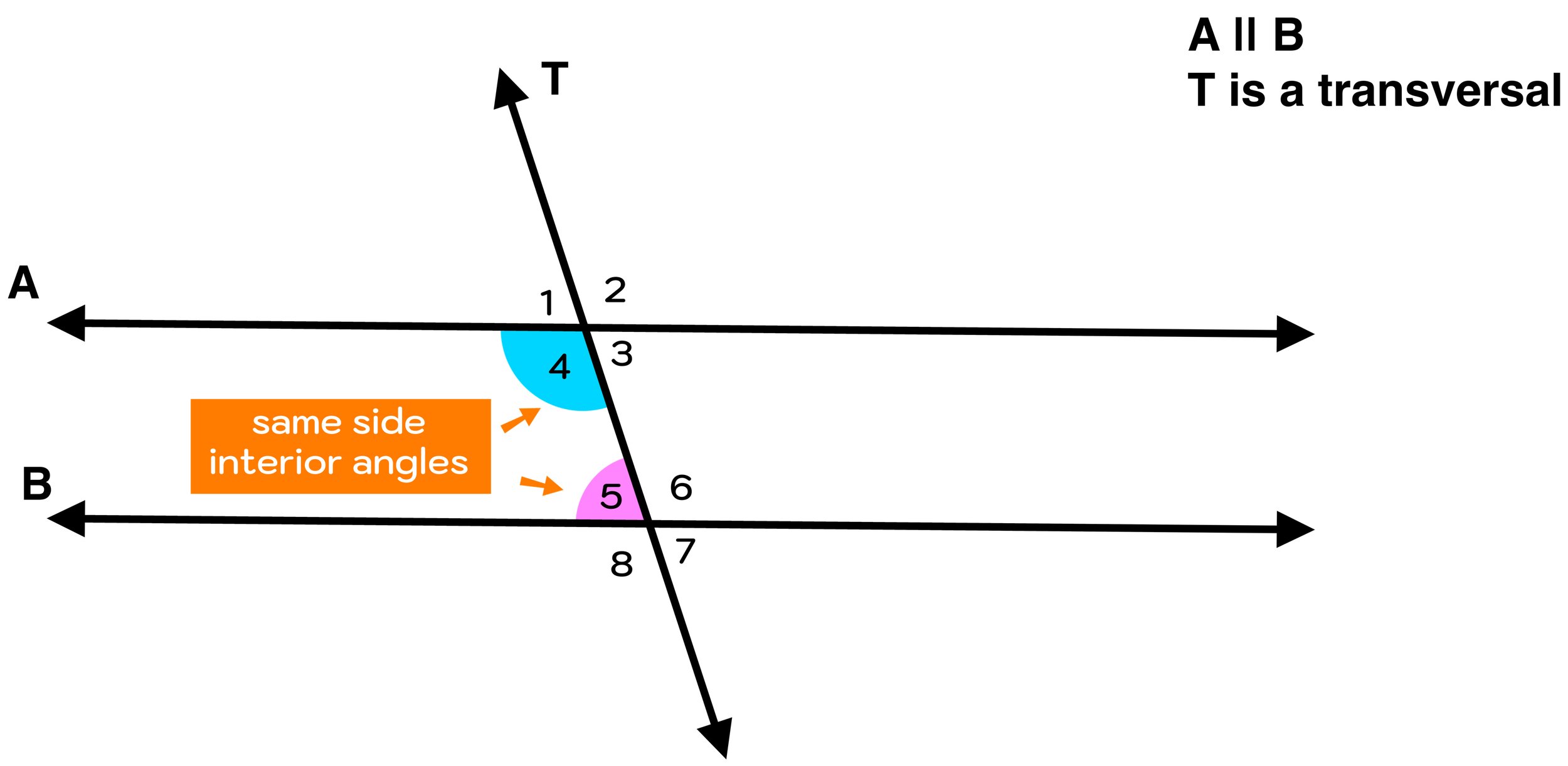
As for identifying same side interior angles, as mentioned earlier, same side interior angles are two angles located on the interior of (or inside) between two parallel lines that are cut by a transversal. In cases like the diagram shown in Figure 01, there will be two sets of same side interior angles,:

∠4 and ∠5 are same side interior angles
∠3 and ∠6 are same side interior angles

These two instances of same side interior angles are shown in Figures 02 and 03 below.

Same Side Interior Angles Theorem

Now that you understand how to identify same side interior angles when given a diagram featuring two parallel lines cut by a transversal, you are ready to learn the Same Side Interior Angles Theorem and what it means.

In Figures 02 and 03 above, we identified two pairs of same side interior angles: ∠4 and ∠5 & ∠3 and ∠6

The Same Side Interior Angle Theorem says that when two parallel lines are cut by a transversal, any pair of same side interior angles will be supplementary—meaning that their sum will equal 180 degrees.

The Same Side Interior Angle Theorem should make sense, as we have already covered that any combination of a pink angle and a blue angle will form a linear pair and be equal to 180 degrees. For example, same side interior angles ∠4 (blue) and ∠5 (pink) meet these requirements and, therefore, have a sum of 180 degrees.

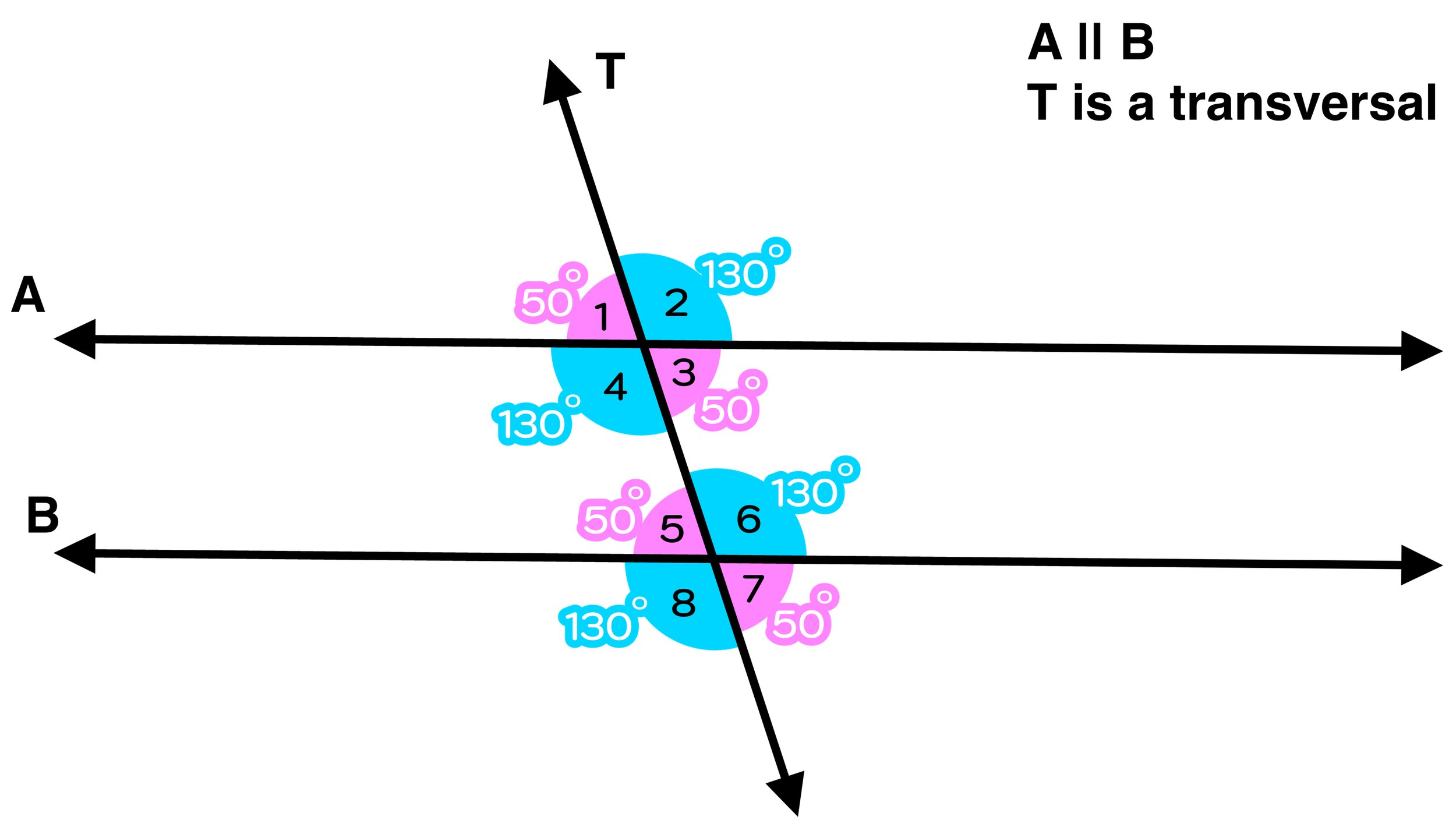
We can visualize why the Same Side Interior Angle Theorem is true by adding angle measures to our original diagram (Figure 01) as shown in Figure 04 below. Notice, again, that:

All of the blue angles are congruent and equal 130 degrees: ∠2=130, ∠4=130, ∠6=130, ∠8=130
All of the pink angles are congruent and equal 50 degrees: ∠1=50, ∠3=50, ∠5=50, ∠7=50
Any combination of a blue angle and a pink angle have a sum of 180 degrees since they are supplementary.
Examples: ∠1 + ∠2 = 180, ∠6 + ∠7 = 180, ∠4 + ∠5 = 180

This relationship is true for any pair of same side interior angles, which is why ∠4 and ∠5 will always be supplementary. Figure 05 below proves why ∠4 and ∠5, which are same side interior angles, are supplementary and have a sum of 180 degrees—according to the Same Side Interior Angle Theorem.

Are same side interior angles supplementary?

Now that you are able to both identify same side interior angles and apply the same side interior angle theorem, you are ready to take on the question: are same side interior angles supplementary?

Remember that two angles are supplementary if and only if their sum is 180 degrees. In Figure 04 above, ∠1 and ∠4 are supplementary because they have a sum of 180 degrees (50+130=180). Conversely, ∠1 and ∠3 are not supplementary because they are vertical angles that are congruent to each other and they do not have a sum of 180 degrees (50+50≠180).

As explored in the previous section, the Same Side Interior Angles Theorem tells us that same side interior angles are supplementary—meaning that they will always add up to 180 degrees.

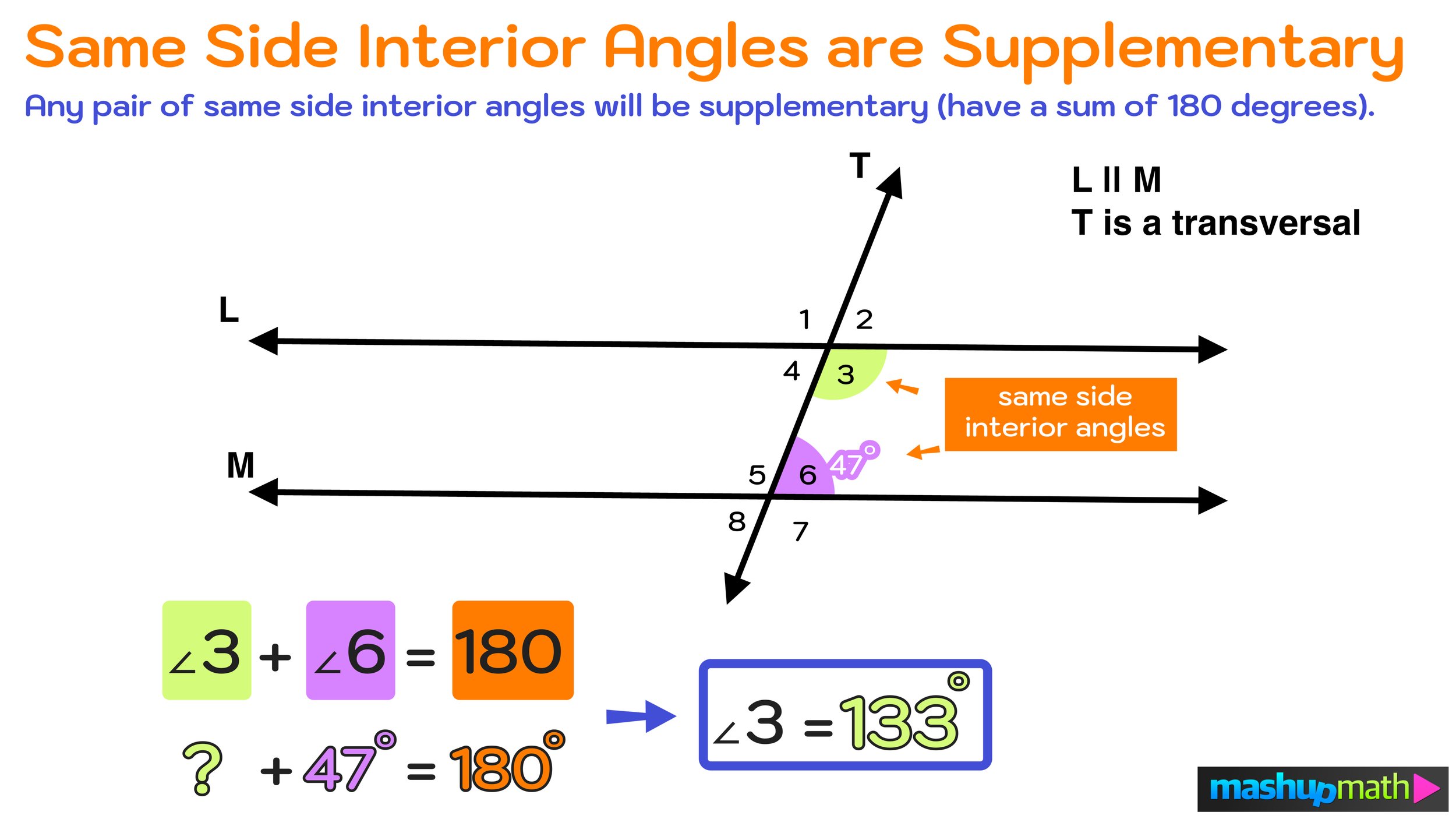
To further demonstrate the same side interior angles supplementary relationship, take a look at Figure 06 below.

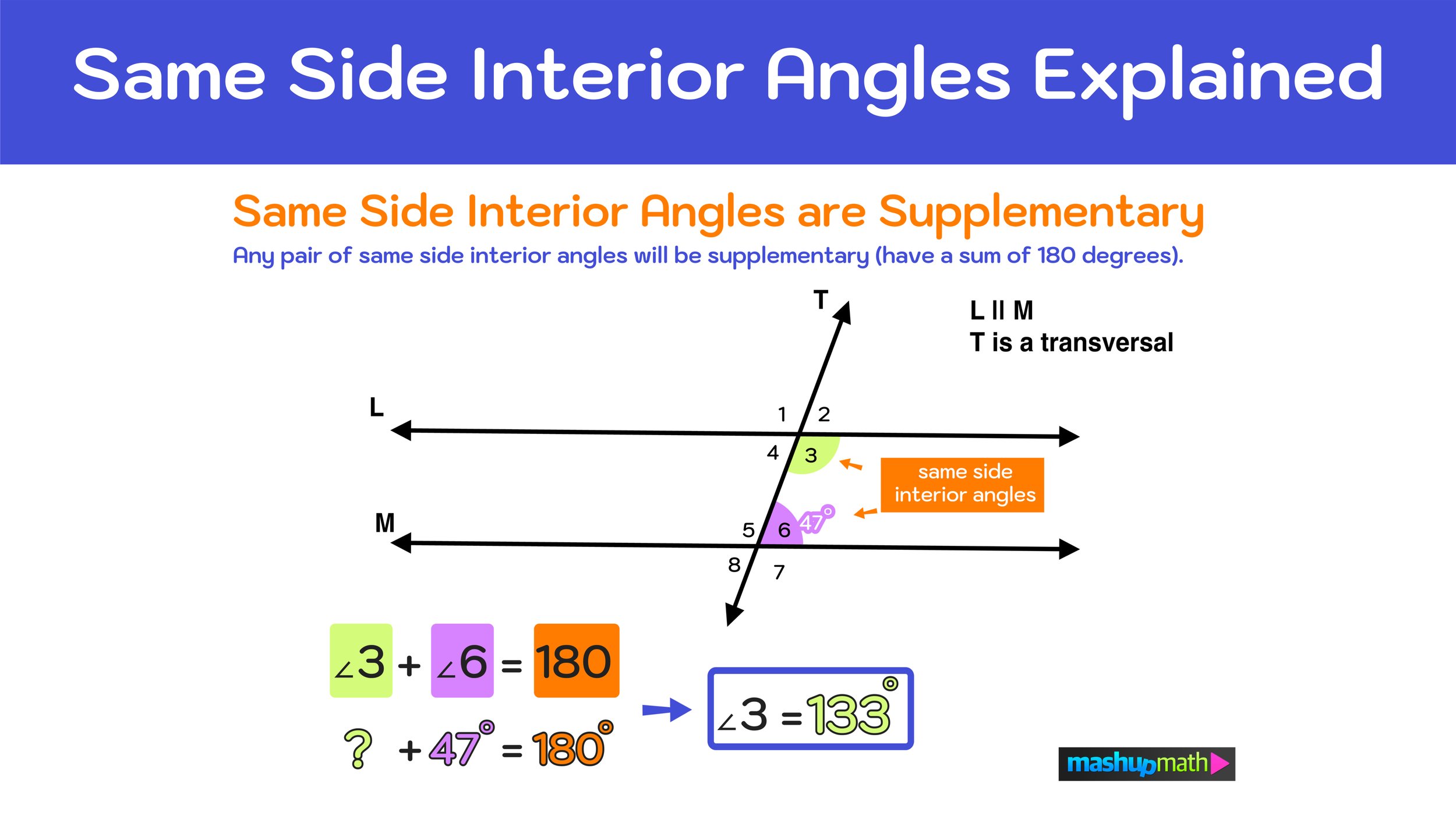
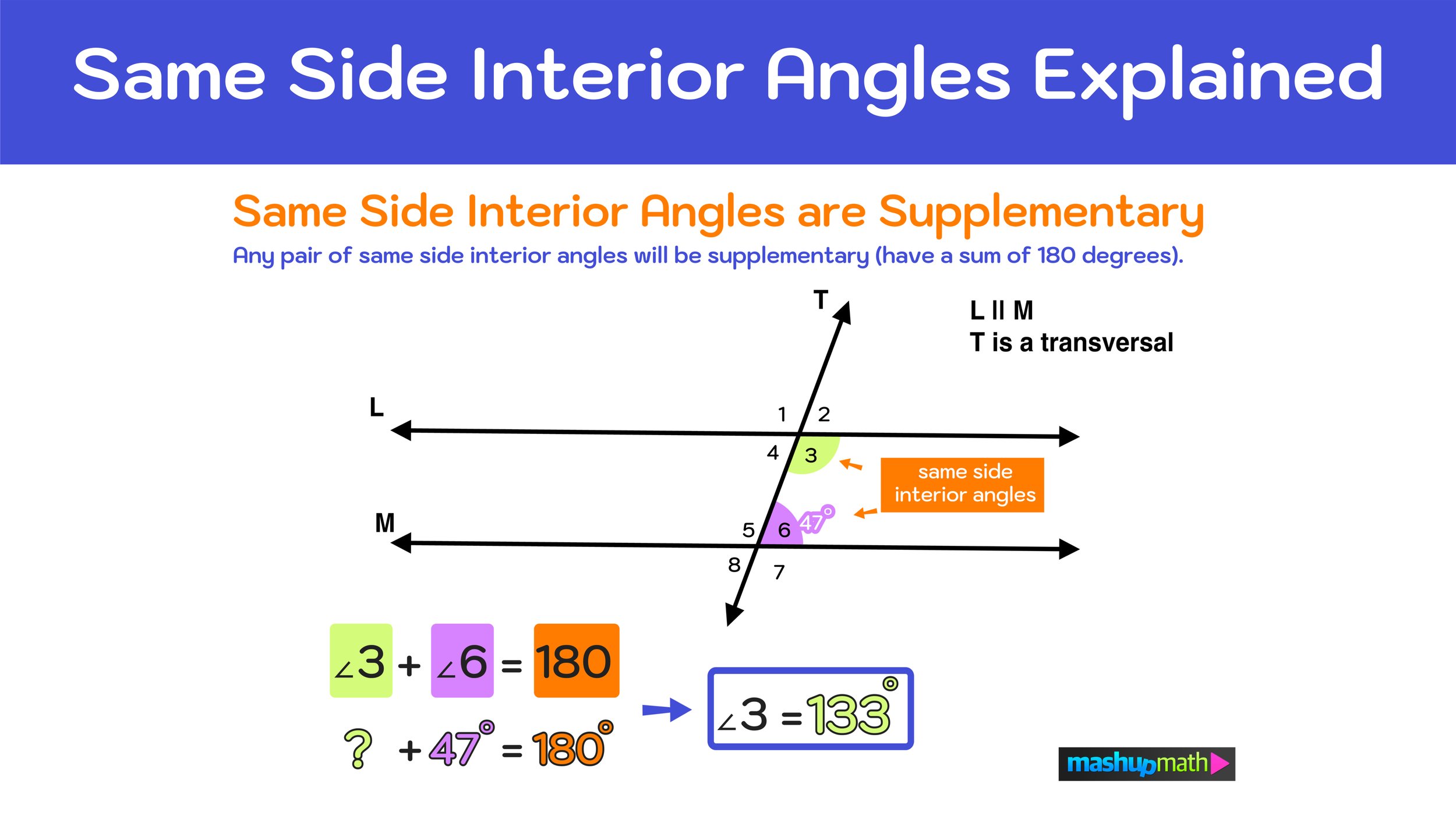
In the figure, lines L and M are parallel and line T is a transversal. Again, there are two pairs of same side interior angles: ∠4 and ∠5 & ∠3 and ∠6. In the diagram, the only angle measure that is given is that ∠6=47. However, by applying the Same Side Interior Angles Theorem and the supplementary same side interior angles relationship previously discussed, you know that, since 3 and ∠6 are same side interior angles, they must have a sum of 180 degrees.

Therefore, you can easily determine the value of ∠3 by solving the following equation:

∠3 + ∠6 = 180 ➔ ∠3 + 47 = 180 ➔ ∠3 = 133 (because 133+47=180)

Now that you have a better understanding of the same side interior angles supplementary relationship, let’s explore one final question related to this topic.

Are same side interior angles congruent?

In this final section, we will purposefully explore the question: are same side interior angles congruent?

Why? Because many students confuse the same side interior angles supplementary relationship with other angle relationships and end up making false assumptions.

As covered in depth in this guide, same side interior angles are supplementary, which means that they form a linear pair and have a sum of 180 degrees.

Conversely, same side interior angles are not congruent because they do not equal to each other. Two angles are only congruent if they have the same angle measure.

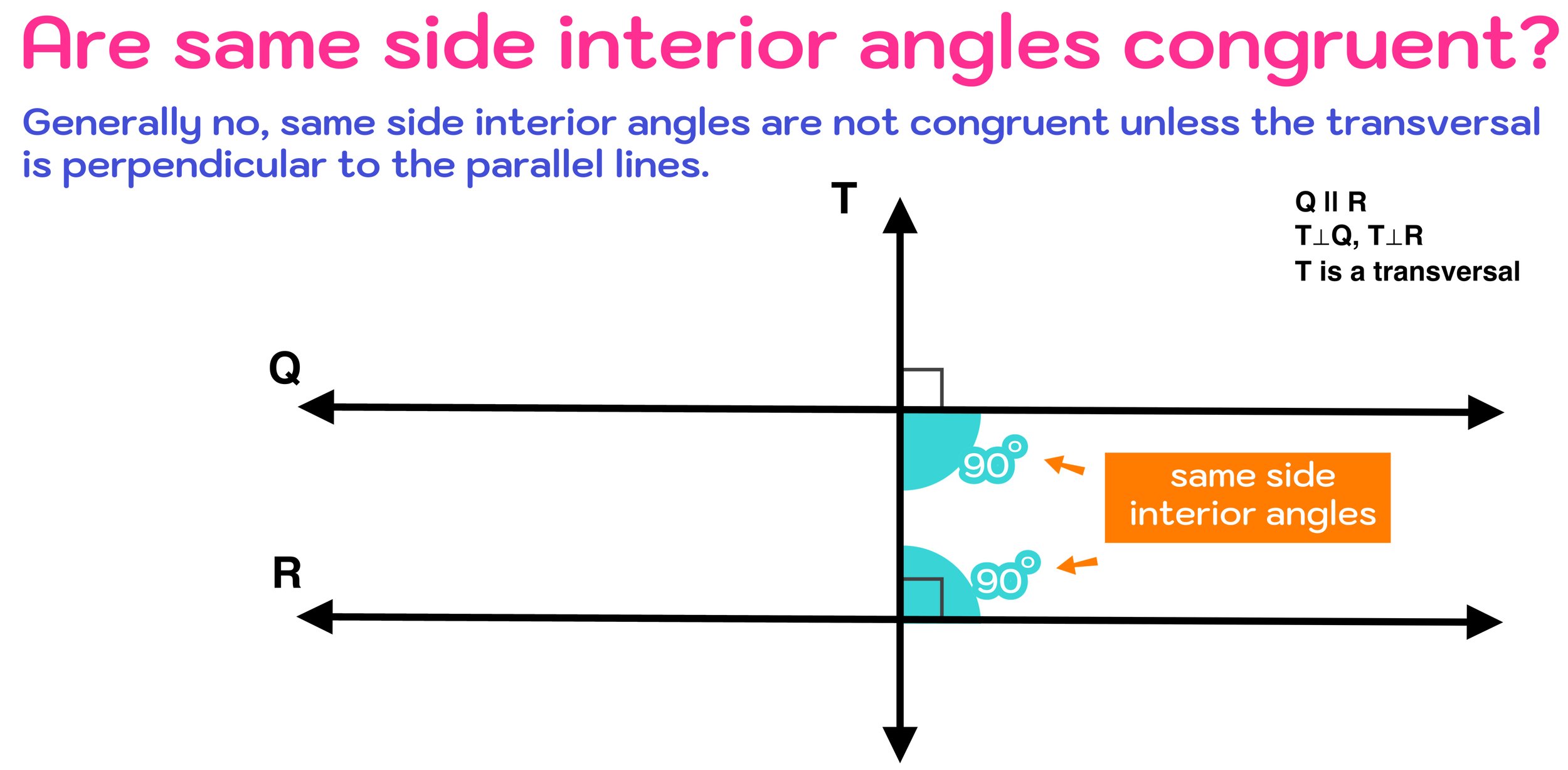
The only instance where same side interior angles can be congruent is when a transversal is perpendicular to two parallel lines, forming 8 right angles that are all congruent to each other (all angles would equal 90 degrees). In this case, both same side interior angles would still be supplementary, since 90+90=180. However, this situation is rare and it is safe to assume that same side interior angles are not congruent.

This rare instance is shown in Figure 07 below. In general, same side interior angles are not congruent, but they are always supplementary.