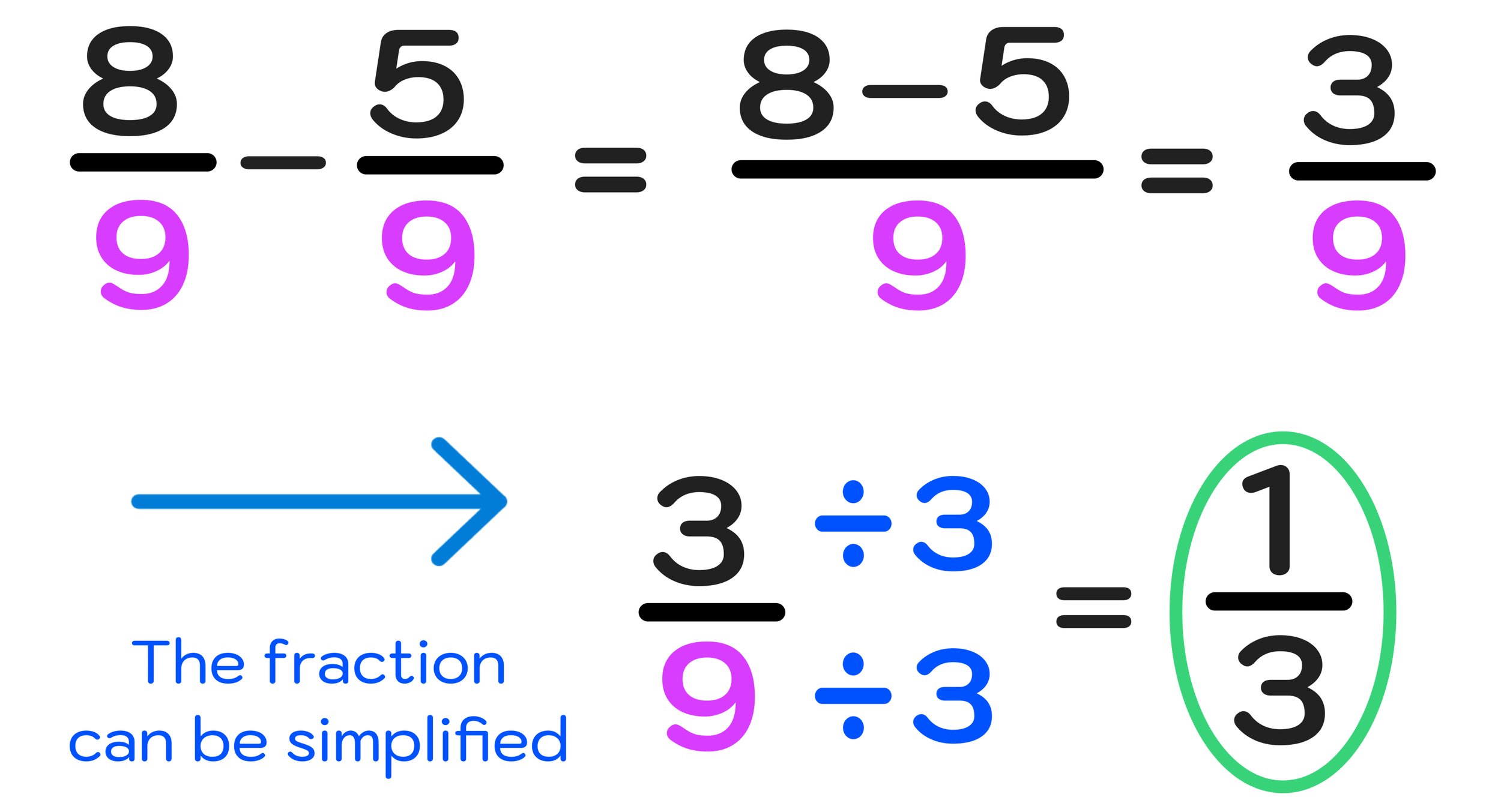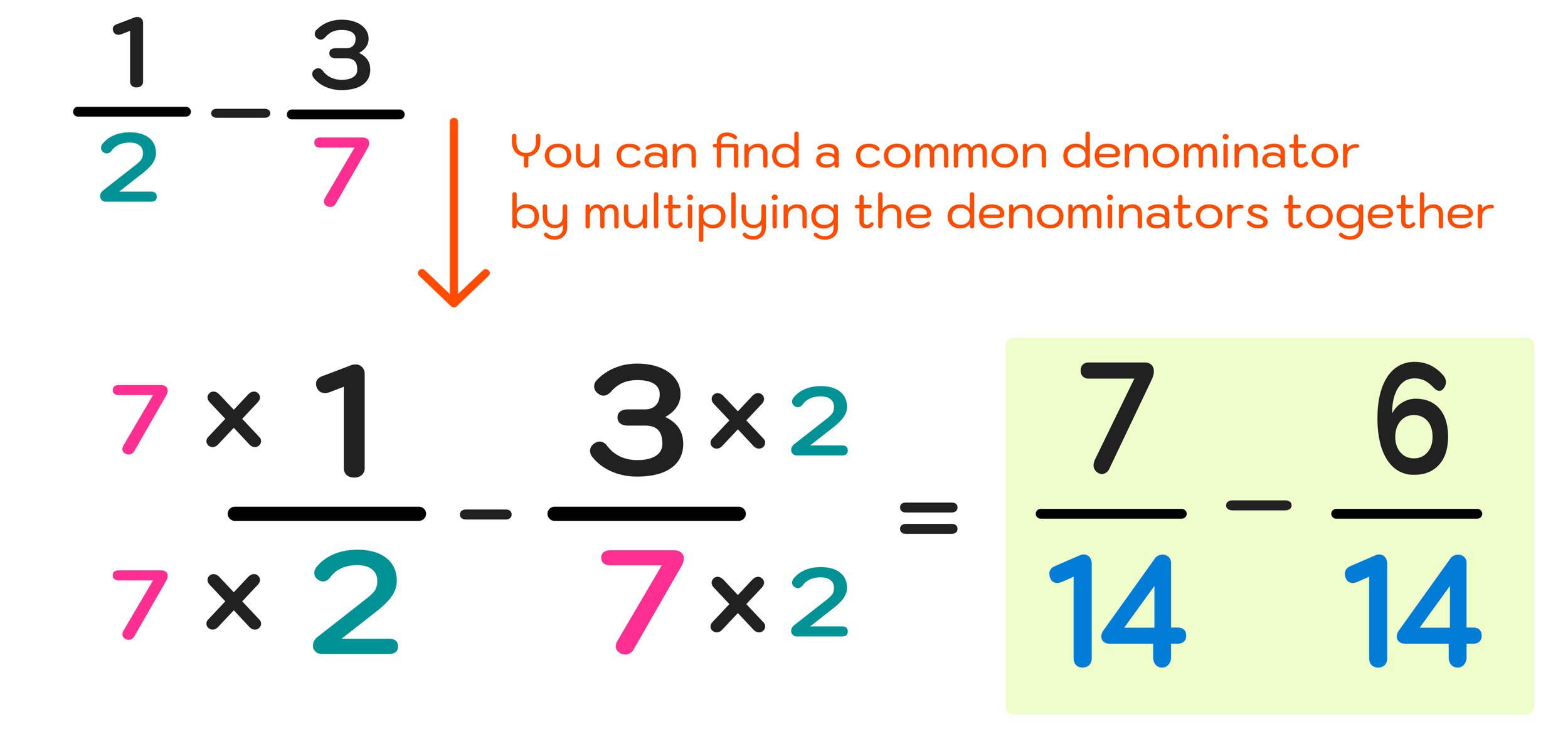How to Subtract Fractions in 3 Easy Steps
Math Skills: How do you subtract fractions with the same denominator and how to subtract fractions with different denominators
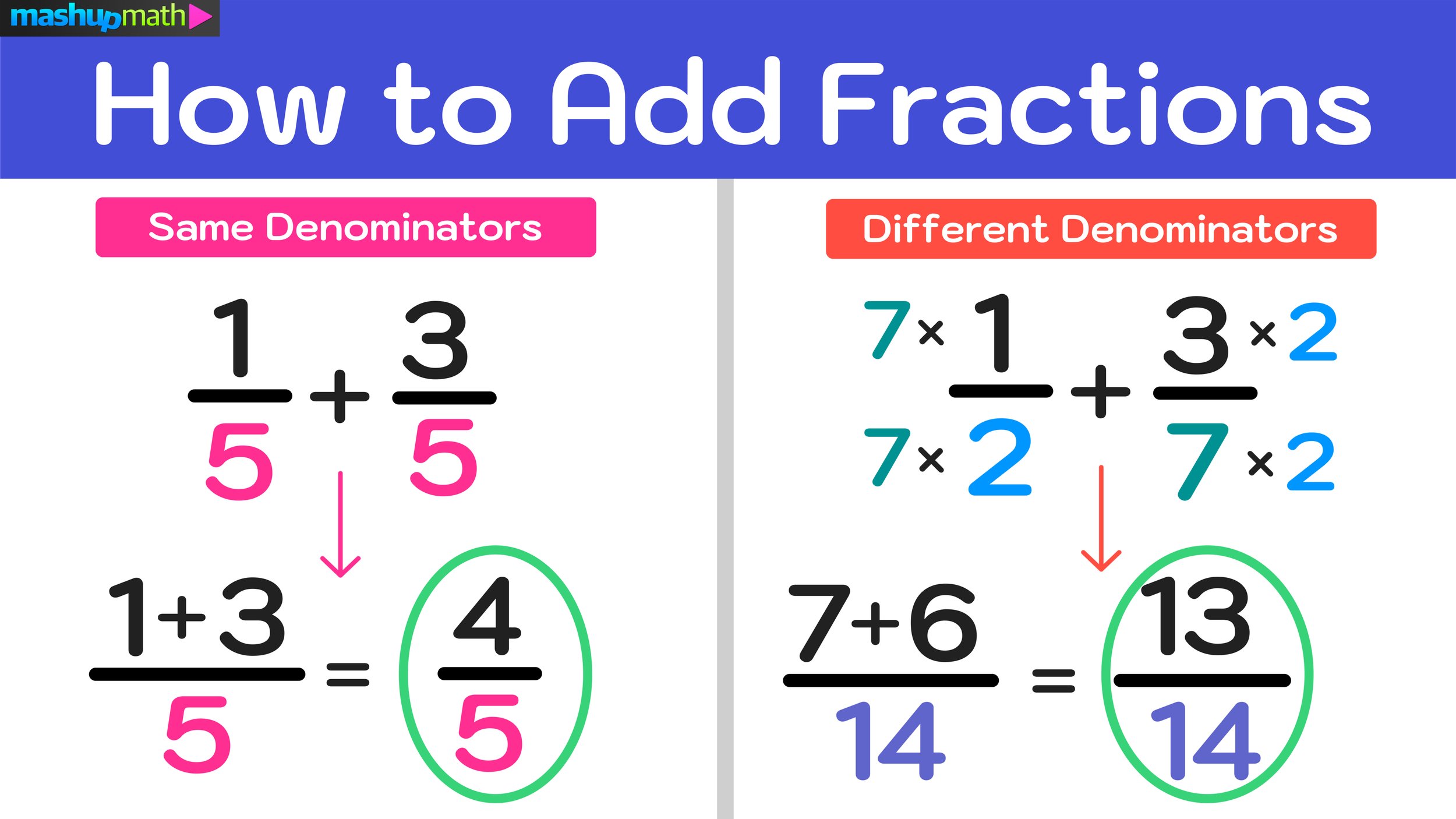
Free Step-by-Step Guide: How do you subtract fractions?
Having the knowledge of how to subtract fractions is a crucial and fundamental math skill that every student must learn, as it serves as a foundational element for comprehending more advanced math ideas that you may come across in the future.
(Looking to learn how to add fractions? Click here to access our free guide)
Fortunately, subtracting fractions, regardless of whether the denominators are the same (like) or different (unlike) can be done using a straightforward and uncomplicated three-step process.
This free Step-by-Step Guide on How to Subtract Fractions will walk you through the process of subtracting fractions with like and unlike denominators, including detailed examples for each scenario.
This step-by-step guide will focus on teaching you the following math skills:
How to subtract fractions with the same denominator?
Subtracting Fractions with Unlike Denominators: How to subtract fractions with different denominators?
Before we cover how to subtract fractions and work through a few examples, let’s do a fast recap of some key characteristics and vocabulary terms related to subtracting fractions.
Let’s get started!
Subtracting Fractions: Definitions and Vocabulary
Before you can learn how to subtract fractions, it’s important for you to know two key vocabulary terms (and the difference between them):
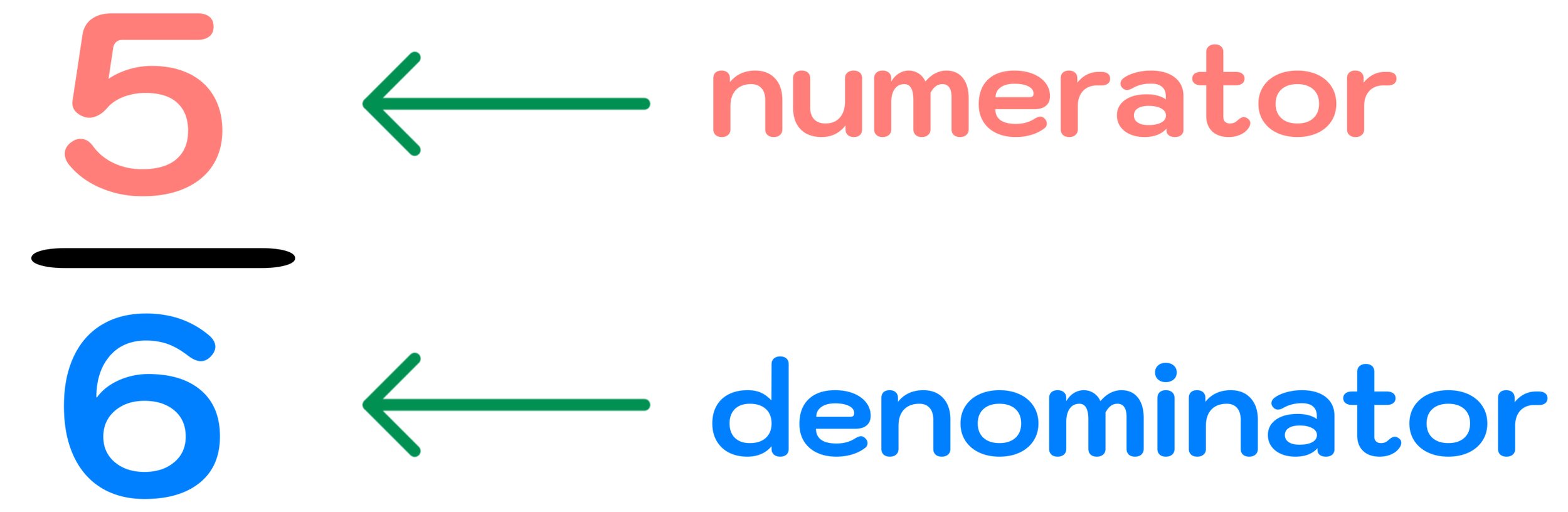
Definition: The top number of a fraction is called a numerator. For example, the fraction 5/6 has a numerator of 5.
Definition: The bottom number of a fraction is called a denominator. For example, the fraction 5/6 has a denominator of 6.
Again, the numerator is the top number of a fraction, and the denominator is the bottom number. These terms are further illustrated in Figure 01 below. While these two math vocabulary terms are simple, it is crucial that you are able to understand and correctly identify the numerator and denominator of fractions in order to master the skill of subtracting fractions.
Figure 01: Fraction Subtraction Key Terms: The numerator of a fraction is the top number, and the denominator is the bottom number.
Moving on, you are ready to take the next step towards mastering fraction subtraction. Next, you will need to be able to determine when a fraction subtraction problem falls into one of the following two categories:
Subtracting Fractions with Like Denominator (the denominators equal the same number)
Subtracting Fractions with Unlike Denominator (the denominators are different)
Fractions that have like denominators have bottom numbers that equal the same value.
Example: 3/5 - 1/5 → This would be a case of subtracting fractions with like denominators since both fractions have a denominator of 5.
Alternatively, fractions that have unlike denominators have bottom numbers that do not equal the same value.
Example: 1/2 - 3/7 →This would be a case of subtracting fractions with unlike denominators since both fractions have different bottom numbers (one has a denominator of 2 and the other has a denominator of 7).
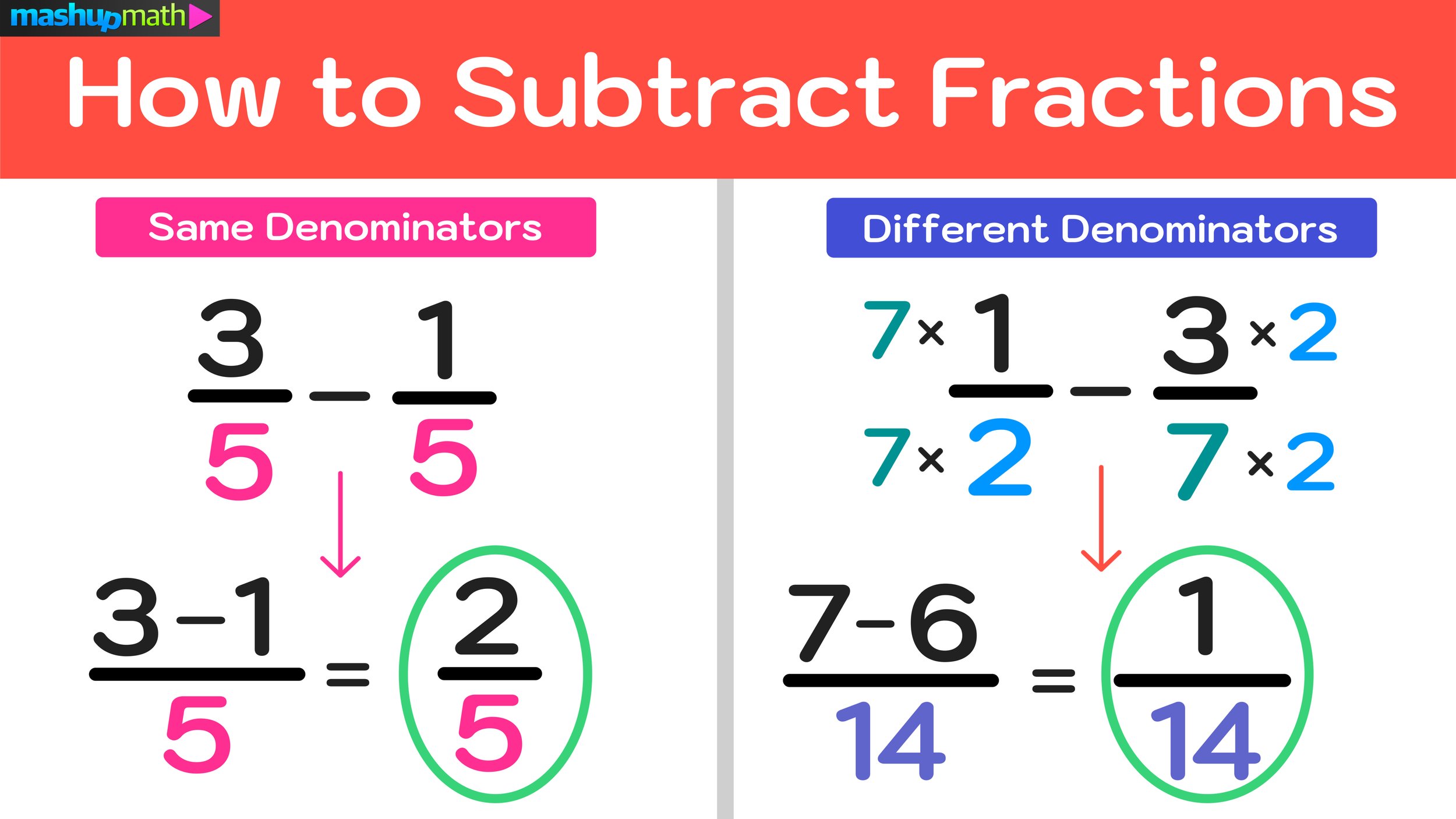
Both examples (one with like denominators and one with unlike denominators) are illustrated in Figure 02 below.
Figure 02: How do you subtract fractions? The first step is being able to identify whether the fractions in question have like denominators or unlike denominators.
This concept may seem uncomplicated, but it is essential to refresh your understanding since you must be able to recognize if a problem involving subtracting fractions has like or unlike denominators in order to find a correct solution.
Now that you have the important foundation skills, you are ready to work through a few fraction subtraction problems.
How to Subtract Fractions with Like Denominators
How to Subtract Fractions with Like Denominators: Example #1
Example #1: 3/5 - 2/5
The first fraction subtraction example is pretty easy and straightforward, which is why it is a good place to start using our simple 3-step process for subtracting fractions. If you can learn to apply these three steps to easy examples, then you will be able to use the same process to solve more complex problems in the future (since the process works for any fraction subtraction problem).
How Do You Subtract Fractions in 3 Easy Steps?
Step One: Identify whether the denominators are the same (like) or different (unlike).
Step Two: If the example involves like denominators, move onto Step Three. If they are unlike denominators, find a common denominator.
Step Three: Subtract the numerators and find the difference.
Now that you know the steps, let’s apply them to solving this first example:
3/5 - 1/5 = ?
Step One: Identify whether the denominators are the same (like) or different (unlike).
The fractions in this example have like denominators. They are both 5.
Step Two: If the example involves like denominators, move onto Step Three. If they are unlike denominators, find a common denominator.
Since the denominators are the same, you can skip ahead to the next step.
Step Three: Subtract the numerators and find the difference.
To complete this fraction subtraction problem, simply subtract the numerators and express the result as follows:
3/5 - 1/5 = (3-1)/5 = 2/5
Since 1/5 can not be reduced, you can conclude…
Final Answer: 2/5
Figure 03 below illustrates how you came to this conclusion.
Figure 03: How to Subtract Fractions with Like Denominators: Subtract the numerators and keep the denominator.
The first example shows you that subtracting fractions with like denominators is pretty easy.
To subtract fractions with the same denominator, subtract the numerators and keep the same denominator.
Now, let’s move onto one more example of subtracting fractions with like denominators before moving onto examples of how to subtract fractions with different denominators.
How to Subtract Fractions with Like Denominators: Example #2
Example #2: 8/9 - 5/9
For the next example, you will be applying the same 3-step method that you used in Example #1 as follows:
Step One: Identify whether the denominators are the same (like) or different (unlike).
In this example, the fractions have like denominators. They are both 9.
Step Two: If the example involves like denominators, move onto Step Three. If they are unlike denominators, find a common denominator.
Again, since the denominators are the same, you can skip ahead to Step Three.
Step Three: Subtract the numerators and find the difference.
To complete this fraction subtraction problem, subtract the numerators as follows:
8/9 - 5/9 = (8-5)/9 = 3/9
In this case, 3/9 is the correct answer, but this fraction can be simplified. Since both 3 and 9 are divisible by 3, 3/9 can be simplified as 1/3.
Final Answer: 1/3
Figure 04 below illustrates how you just solved Example #2.
Figure 04: Subtracting Fractions: 3/9 can be simplified to 1/3
Now, let’s move onto learning how to subtract fractions with different denominators.
How to Subtract Fractions with Different Denominators
How to Subtract Fractions with Different Denominators: Example #1
Example #1: 1/2 - 3/7
Step One: Identify whether the denominators are the same (like) or different (unlike).
In this example, the fractions have unlike denominators (they are different). The first fraction’s denominator is 2 and the other’s is 7.
Step Two: If the example involves like denominators, move onto Step Three. If they are unlike denominators, find a common denominator.
Since the fractions have unlike denominators, you can not skip ahead.
Before you can move onto Step Three, you have to find a number that both denominators can divide into evenly. This is called a common denominator.
A very easy and effective way to find a common denominator between two fractions is by multiplying the denominators together (i.e. multiplying the denominator of the first fraction by the second fraction and multiplying the denominator of the second fraction by the first fraction.
1/2 - 3/7 (1x7)/(2x7) - (3x2)/(7x2) = 7/14 - 6/14
This fraction subtraction process is illustrated in Figure 05 below.
Figure 05: How to Subtract Fractions with Different Denominators: Find a common denominator by multiplying the denominators together.
(Looking for some extra help with multiplying fractions, click here to access our free student guide).
Now that Step Two is complete, you can see that the original question has been transformed and you are now working with equivalent fractions that have common denominators, which means that the heavy lifting has been done and you can now solve the problem by subtracting the numerators and keep the same denominator:
7/14 - 6/14 = (7-6)/14 = 1/14
Since 1/14 can not be reduced further, you have solved the problem…
Final Answer: 1/14
Figure 06: Once you have common denominators, simply subtract the numerators keep the same denominator.
Are you ready for one more practice problem for how to subtract fractions with unlike denominators?
How to Subtract Fractions with Different Denominators: Example #2
Example #1: 2/3 - 8/15
For this final example of subtracting fractions, you will again be using the 3-step method as follows:
Step One: Identify whether the denominators are the same (like) or different (unlike).
The fractions have unlike denominators (one is 3 and the other is 5).
Step Two: If the example involves like denominators, move onto Step Three. If they are unlike denominators, find a common denominator.
Just like last example, you will have to find a common denominator since the fractions have unlike denominators. You can find a common denominator by multiplying the denominators together as follows:
(2x15)/(3x15) - (8x3)/(15x3) = 30/45 - 24/45
This process is shown in Figure 07 below.
Figure 07: How to Subtract Fractions with Different Denominators
Now that the fractions share a common denominator, you can solve the fraction subtraction problem as follows:
30/45 - 24/45 = (30-24)/45 = 6/45
Since both 6 and 45 are divisible by 3, you can simplify this fraction as…
Final Answer: 2/15
Figure 08: Subtracting Fractions with Unlike Denominators
Conclusion: How to Subtract Fractions
Subtracting fractions with like denominators involves simply finding the difference of the numerators (top values) and not changing the denominator (bottom value).
Subtracting fractions with unlike denominators requires you to find a common denominator, which is a value that both denominators divide evenly into.
How do you subtract fractions? You can solve any fraction subtraction problem by applying the following three step method:
Step One: Identify whether the denominators are the same (like) or different (unlike).
Step Two: If the example involves like denominators, move onto Step Three. If they are unlike denominators, find a common denominator.
Step Three: Subtract the numerators and find the difference.
Keep Learning:
Search Tags: how to subtract fractions, subtracting fractions, how to subtract fractions with different denominators, fraction subtraction, subtracting fractions with unlike denominators, how do you subtract fractions?