Is a Rhombus a Parallelogram? Yes or No?

Explore the unique features of a rhombus and a parallelogram to determine whether or not a rhombus is both

 

Is a rhombus a parallelogram? Is a parallelogram a rhombus? Let’s explore!

 

It’s time to explore and answer the controversial math question: Is a rhombus a parallelogram? Yes or No? This short guide will help you to understand the following concepts:

What is a Rhombus?

Why was the geometry student late for school? Because he took the rhombus!

Okay, jokes aside, let’s quickly explore the features and characteristics of a rhombus and a parallelogram.

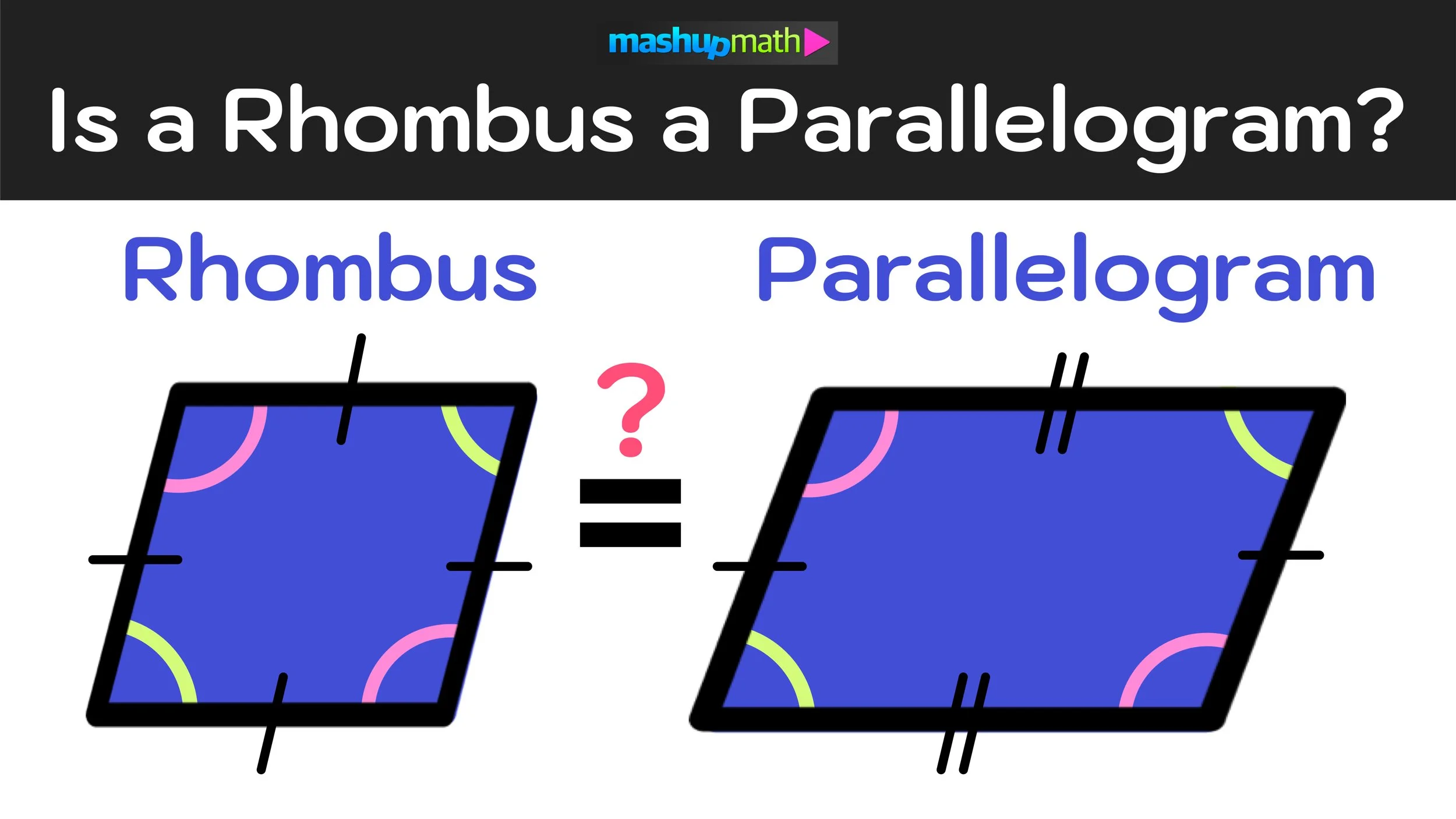
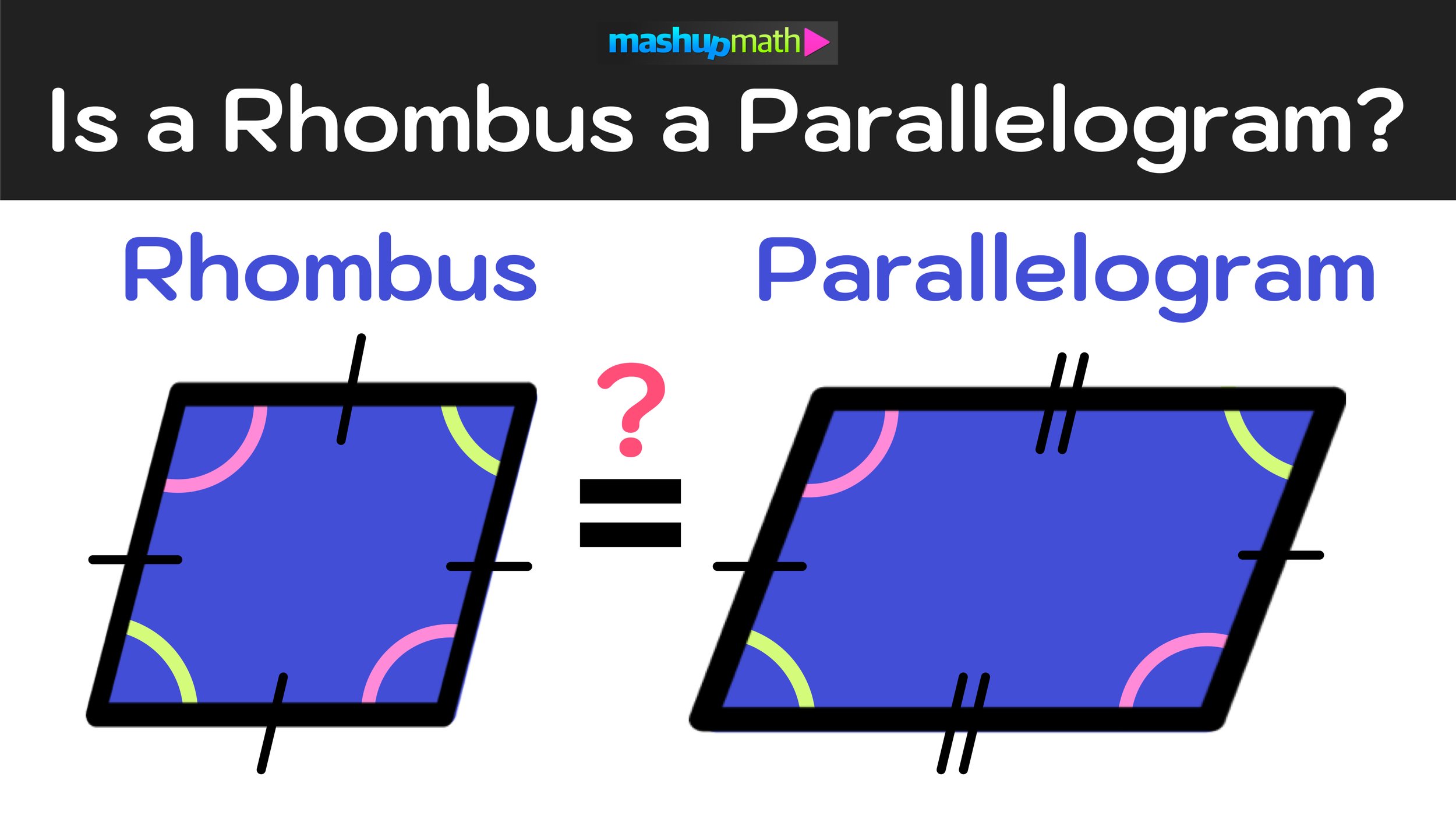
In geometry, a rhombus is a four-sided figure (quadrilateral) where all four sides have the same length and opposite sides are parallel to each other. Additionally, the opposite interior angles of any rhombus are equal to each other (congruent).

 

Is a rhombus a parallelogram? Start by knowing exactly what a rhombus is.

 

What is a Parallelogram?

In geometry, a parallelogram is a four-sided figure (quadrilateral) where opposite sides have the same length and are parallel to each other, but all four sides do not have to be equal. Similar to a rhombus, the opposite interior angles of any parallelogram are congruent.

The key feature of a parallelogram is that the opposite sides are both equal in length and parallel to each other—hence the name parallelogram.

 

Is a rhombus a parallelogram? Continue by learning the definition of a parallelogram.

 

What is the Difference Between a Rhombus and a Parallelogram?

Now that you know the key characteristics of a rhombus and a parallelogram, let’s explore what sets them apart.

For starters, a rhombus and a parallelogram are similar in that they are both quadrilaterals, meaning that they are four sides figures. They also both have opposite sides that are equal in length to each other and they both have sets of opposite interior angles that are congruent to each other.

However, the key differences between a rhombus and a parallelogram are that a parallelogram has two sets of parallel sides that are equal in length, while a rhombus has four sides that are all equal in length.

So, a parallelogram is like a rectangle that doesn’t have right angles, while a rhombus is like a square that doesn’t have right angles.

 

What is the Difference Between a Rhombus and a Parallelogram?

 

The key takeaway concerning the difference between a rhombus and a parallelogram is that they both have opposite sides that are parallel and congruent (and opposite interior angles that are congruent), but a rhombus has to have four equal sides, but a parallelogram does not.

Is a Rhombus a Parallelogram? Yes or No?

The answer is YES—by definition, a rhombus is a parallelogram.

Again, by definition, a parallelogram is quadrilateral with two pairs of parallel sides with opposite interior angles that are congruent. A rhombus is just a special type of parallelogram where all four of the sides are equal in length. As for interior angles, the opposite interior angles of a rhombus are congruent just as they are in a parallelogram.

Is a rhombus always a parallelogram?

To say that every rhombus is a parallelogram would be true.

Since the properties of a rhombus satisfy the definition of a parallelogram and we can conclude that:

  • Is a rhombus always a parallelogram? Yes!

  • A rhombus is a special type of parallelogram—namely, one where all four sides are equal in length.

  • All rhombuses are parallelograms.

 

Is a rhombus always a parallelogram? Yes, a rhombus is a special type of parallelogram—namely, one where all four sides are equal in length.

 

It is important to note that the conclusion that we just made is not an opinion, but a mathematical fact.

All rhombuses are parallelograms. In fact, a rhombus is a subset of a parallelogram in that it is special because it is a parallelogram with four congruent sides.

This explanation is very similar to our exploration of the question is a square a rectangle?, where we similarly concluded that a square is a special type of rectangle and that all squares are rectangles.

Next, let’s consider if the opposite is true: is a parallelogram a rhombus?

 

Is a Parallelogram a Rhombus? No. All Oreos are cookies, but not all cookies are Oreos (because Oreos are a special type of cookie). Similarly, every rhombus is a parallelogram, but every parallelogram is not necessarily a rhombus.

 

Is a Parallelogram a Rhombus? Yes or No?

We have just applied the mathematical definition of a rhombus and parallelogram to prove that a rhombus is indeed a parallelogram. We concluded that a rhombus is a special type of parallelogram that has all of the characteristics of a parallelogram and four congruent sides.

But, is a parallelogram a rhombus?

No. By definition, a parallelogram does not necessarily have to be a rhombus.

Remember that a parallelogram is a quadrilateral with two pairs of sides that have to be parallel and equal in length, but it does not need to have all four sides be congruent.

Again, a rhombus is like a square and a parallelogram is like a rectangle. Similarly, all squares are rectangles, but not all rectangles are squares.

To say that every parallelogram is a rhombus would be false.

Therefore, while every rhombus is a parallelogram, not all parallelograms are rhombuses.

Conclusion: Is a Rhombus a Parallelogram?

In this short lesson, you learned that both a rhombus and a parallelogram are quadrilaterals with opposite sides that are equal in length and opposite interior angles that are congruent. You also learned that a rhombus is a special type of parallelogram—namely one that has four congruent sides.

As for the question, is a rhombus a parallelogram? The answer is yes! All rhombuses are parallelograms, but not all parallelograms are rhombuses.

More Math Education Insights You Will Love:

2 Comments