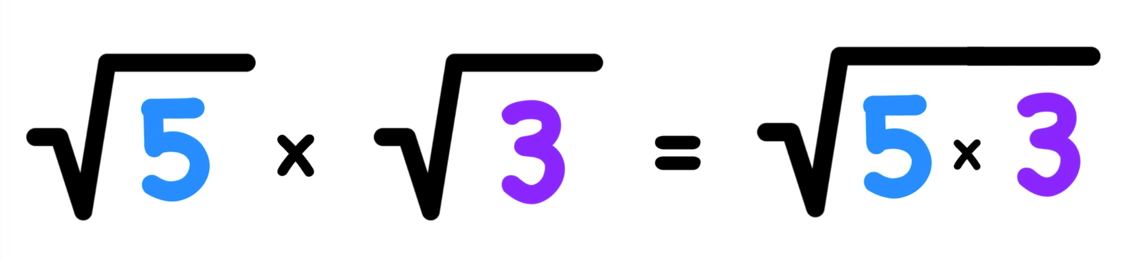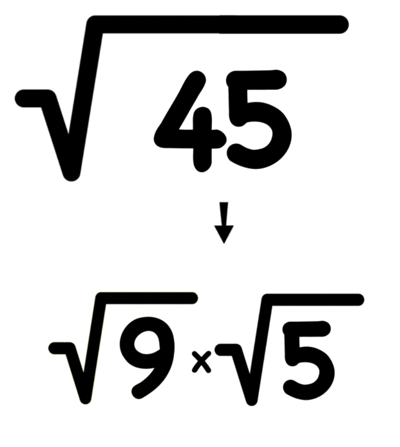What is the Cube Root of...

What is the Cube Root of…

The following reference posts shares the cube roots of the most often searched values.

What is a cube root?

The cube root of a number is the value that produces that number when cubed.

For example, the cube root of 64 is 4 because 4^3 (4x4x4) equals 64.

What is the Cube Root of 1?

The cube root of 1 is 1 because 1x1x1=1.

What is the Cube Root of 8?

The cube root of 8 is 2 because 2x2x2=8.

What is the Cube Root of 27?

The cube root of 27 is 3 because 3x3x3=9.

What is the Cube Root of 64?

The cube root of 64 is 4 because 4x4x4=64.

What is the Cube Root of 125?

The cube root of 125 is 5 because 5x5x5=125.

Download your free Perfect Cubes and Cube Roots reference sheet.

What is the Cube Root of 216?

The cube root of 216 is 6 because 6x6x6=216

What is the Cube Root of 343?

The cube root of 343 is 7 because 7x7x7=343

What is the Cube Root of 512?

The cube root of 512 is 8 because 8x8x8=512

What is the Cube Root of 729?

The cube root of 729 is 9 because 9x9x9=729

What is the Cube Root of 1000?

The cube root of 1000 is 10 because 10x10x10=1000

What is the Cube Root of 1331?

The cube root of 1331 is 11 because 11x11x11=1331

What is the Cube Root of 1728?

The cube root of 1728 is 12 because 12x12x12=1728

What is the Cube Root of 2196?

The cube root of 2196 is 13 because 13x13x13=2196

What is the Cube Root of 2744?

The cube root of 2744 is 14 because 14x14x14=2744

What is the Cube Root of 3375?

The cube root of 3375 is 15 because 15x15x15=3375

What is the Cube Root of 4096

The cube root of 4096 is 16 because 16x16x16=4096

What is the Cube Root of… (Special Cases)

What if a cube root is not a whole number?

If a number is not a perfect cube, it’s cube root will be a decimal.

What is the Cube Root of 2?

The cube root of 2 is approximately 1.26 because 1.26x1.26x1.26 ≈ 2

What is the Cube Root of 3?

The cube root of 3 is approximately 1.44 because 1.44x1.44x1.44 ≈ 3

What is the Cube Root of 4?

The cube root of 4 is approximately 1.59 because 1.59x1.59x1.59 ≈ 4

What is the Cube Root of 9?

The cube root of 9 is approximately 2.08 because 2.08x2.08x2.08 ≈ 9

What is the Cube Root of 16?

The cube root of 16 is approximately 2.52 because 2.52x2.52x2.52 ≈ 16

What is the Cube Root of 81?

The cube root of 81 is approximately 4.33 because 4.33x4.33x4.33 ≈ 81

Learn How to Graph Cube Roots and Cubic Functions:

Share your ideas, questions, and comments below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

Need Practice Finding Cube Roots?

Click the link below to download your free perfect cubes and cube roots practice worksheet:

PDF: Perfect Cubes and Cube Roots Practice Worksheet

Keep Learning:

Multiplying Square Roots and Multiplying Radicals Explained

Learn How to Multiply Radicals and How to Multiply Square Roots in 3 Easy Steps (Free Worksheet Included)

Learn How to Multiply Radicals (and How to Multiply Square Roots) in 3 Easy Steps

Before you learn how to multiply radicals and how to multiply square roots, you need to make sure that you are familiar with the following vocabulary terms:

Radical vs. Radicand

The radical is the square root symbol and the radicand is the value inside of the radical symbol. The radicand can include numbers, variables, or both.

The Multiplication Property of Square Roots

The key to learning how to multiply radicals is understanding the multiplication property of square roots.

The property states that whenever you are multiplying radicals together, you take the product of the radicands and place them under one single radical.

For example, radical 5 times radical 3 is equal to radical 15 (because 5 times 3 equals 15).

How to Multiply Radicals and How to Multiply Square Roots Example

Now let’s take a look at an example of how to multiply radicals and how to multiply square roots in 3 easy steps.

Problem:

Step One: Simplify the Square Roots (if possible)

In this example, radical 3 and radical 15 can not be simplified, so we can leave them as they are for now.

Step Two: Multiply the Radicands Together

Now you can apply the multiplication property of square roots and multiply the radicands together. In this case, radical 3 times radical 15 is equal to radical 45 (because 3 times 15 equals 45).

Step Three: Simplify the Result (if possible)

The third and final step is to simplify the result if possible.

Can radical 45 be simplified?

The answer is yes.

Since radical 45 is equal to radical 9 times radical 5, and because radical 9 is equal to 3 (since 9 is a perfect square), we can simplify radical 45 to 3 times radical 5 (see the diagram below for a more detailed look on how to simplify square roots).

Finally, we can conclude that the final answer is:

Looking for more sample problems? Check out the free video lesson below to learn more about how to multiply radicals and how to multiply square roots :

---

How to Multiply Radicals and How to Multiply Square Roots Worksheet (with Answer Key)

Are you looking to get some more practice with multiplying radicals, multiplying square roots, simplifying radicals, and simplifying square roots?

Click the link below to access your free practice worksheet from Kuta Software:

Free Multiplying Radicals Worksheet

Share your ideas, questions, and comments below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

Keep Learning:

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Negative Exponent Rule Explained in 3 Easy Steps

Understanding the Negative Exponent Rule

Before you learn to understand and apply the Negative Exponent Rule, let’s recap what you already know about positive exponents.

For example, 5^2, or 5 squared, is equal to 5x5, or 25.

But what would change if the exponent (2 in this case) was negative instead of positive?

In math, when you think of the word negative or negate, the implication is that you must perform the opposite or inverse operation.

With positive exponents, you perform multiplication.

So, with negative exponents, you perform the opposite or inverse of multiplication, which is…

Division (because division is the inverse operation of multiplication).

Now you are ready to use the Negative Exponent Rule

Negative Exponent Rule in 3 Easy Steps

Now let’s look at the previous example again, except this time the exponent is -2 (negative two).

Step One: Rewrite the Value with Negative Exponent as a Fraction

Since we are performing division (the inverse of multiplication), we will rewrite the value as a fraction with a numerator of one.

Step Two: Trash the Negative Sign and Move the Value to the Denominator

To complete the fraction, get rid of the negative sign in front of the exponent and move the remaining value (5 squared) to the denominator of the fraction.

Notice that 5 to the negative second power is equal to one over 5 to the positive second power.

via GIPHY

Step Three: Trash the Negative Sign and Move the Value to the Denominator

The final step is to simplify rewriting 5 squared as 25 and concluding that 5^-2 is equal to 1/25 or 0.04.

Expressed as a fraction.

Expressed as a decimal.

Looking for a visual representation of how the negative exponent rule works?

Check out the free video lesson below to learn more about how the negative exponent rule.

---

Free Negative Exponents Worksheet

This lesson includes a free Negative Exponent Rule worksheet that accompanies the video lesson. Click the link below to get yours!

Download your free Negative Exponents Worksheet Lesson Guide PDF

Share your ideas, questions, and comments below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Box and Whisker Plots Explained in 5 Easy Steps

Box and Whisker Plot Definition

Source: Mashup Math MJ

A box and whisker plot is a visual tool that is used to graphically display the median, lower and upper quartiles, and lower and upper extremes of a set of data.

Box and whisker plots help you to see the variance of data and can be a very helpful tool.

This guide to creating and understanding box and whisker plots will provide a step-by-step tutorial along with a free box and whisker plot worksheet.

Let’s get started by looking at some basketball data!

How to Make a Box and Whisker Plot

Observe the following data set below that shares a basketball players points scored per game over a seven-game span:

Step One: The first step to creating a box and whisker plot is to arrange the values in the data set from least to greatest.

In this example, arrange the points scored per game from least to greatest.

Step Two: Identify the upper and lower extremes (the highest and lowest values in the data set).

The lower extreme is the smallest value, which is 5 in this example.

The upper extreme is the highest value, which is 32 in this example.

Step Three: Identify the median, or middle, of the data set.

In this example, the median is 17.

See Also: Check Out This Awesome Mean, Median, and Mode Activity

Step Four: Identify the upper and lower quartiles.

To find the lower quartile and the upper quartile, start by splitting the data set at the median into lower and upper regions.

The upper quartile is the median of the upper region, and the lower quartile is the median of the lower region.

In this example, the upper quartile is 20 and the lower quartile is 10.

Now we have all of the information that we will need to construct our box and whisker plot!

Step Five: Construct the Box and Whisker Plot

To construct a box and whisker plot, start by drawing a number line that fits the data set.

Start by plotting points over the number line at the lower and upper extremes, the median, and the lower and upper quartiles.

Next, construct two vertical lines through the upper and lower quartiles, and then constructing a rectangular box that encloses the median value point.

Then construct a vertical line through the median point that extends to the top and bottom of the rectangle.

This is the box in the box and whisker plot.

Finally, draw horizontal lines that connect the lower quartile to the lower extreme and the upper quartile to the upper extreme to complete the box and whisker plot.

The box and whisker plot is complete!

Box and Whisker Plot Worksheet

Are you looking to get some more practice with making and analyzing box and whisker plots?

Check out the following free box and whisker plot worksheet, which is available as a PDF download!

Click here to download your free Box and Whisker Plot worksheet.

Answer key included.

Box and Whisker Plot Video Lesson

Check out our free Box and Whisker Plots Explained video lesson on YouTube for a more in-depth look:

Tags:  box and whisker plot explained, box and whisker plot definition, box and whisker plot problems, box and whisker plot outliers, box and whisker plot worksheet, box and whisker plot range

---

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Related Posts:

Are Your Kids Ready for These Halloween Math Activities?

Are You Ready to Celebrate Halloween with Your Math Students This Year?

Are your students excited to celebrate Halloween this year?

If so, then you can channel their enthusiasm for this spooky time of year towards learning math with some brand new Halloween-themed two truths and one lie math activities for grades 3-8.

Go ahead and share these activities at any point during your math lessons this month to boost student engagement and bring some holiday festiveness into your classroom. You may also like our 13 Days of Spooky Math Puzzles and these fun hands-on Halloween math activities for all ages. Enjoy!

Image Source: Mashup Math FP

The following Halloween Math Activities for elementary and middle school students are samples from my best-selling PDF math workbooks: 101 Two Truths and One Lie! Math Activities for Grades 3-5 and 101 Two Truths and One Lie! Math Activities for Grades 6-8.

Two Truths and One Lie (2T1L) math activities revolve around your students being presented with three facts, images, or statements (only two of which are true). The objective is for students to identify which statement is false and justify why (verbally, in writing, or both).

2T1L activities are an excellent strategy for boosting student engagement, sparking mathematical thinking, and opening small-group or full-class discussions. They are great for warm-up and cool-down activities during the first or final minutes of class.

Click here to learn more about how you can use two truths and one lie math activities to engage your students.

Free Halloween Math Activities for Grades 3, 4, and 5

(keep reading to get puzzles for grades 6, 7, and 8)

View fullsize

3rd Grade

View fullsize

4th Grade

View fullsize

5th Grade

Answer Key: 3rd Grade: 3 | 4th Grade: 2 | 5th Grade: 2

You can learn more about 2T1L activities and access more free samples here.

---

Wait! Get 100+ More Two Truth and One Lie Math Activities for Your Students!

---

Free Halloween Math Activities for Grades 6, 7, and 8

View fullsize

6th Grade

View fullsize

7th Grade

View fullsize

8th Grade

Answer Key: 6th Grade: 2 | 7th Grade: 2 | 8th Grade: 1

You can learn more about 2T1L activities and access more free samples here.

Looking for more Two Truths and One Lie Math Activities?

You can now share 101 Daily Two Truths & One Lie! Math Activities for Grades 3, 4, & 5 OR Grades 6, 7, & 8 with your kids with our brand new PDF workbooks!

Here are a few more free samples that you can download and share with your kids (right-click to download each graphic and save it to your computer):

• 3rd Grade: Sample A | Sample B

• 4th Grade: Sample A | Sample B

• 5th Grade: Sample A | Sample B

Looking for more for grades 3, 4, & 5? Download your 101 ‘Two Truths and One Lie!’ Math Activities for Grades 3, 4, & 5 eBook!

• 6th Grade: Sample A | Sample B

• 7th Grade: Sample A | Sample B

• 8th Grade: Sample A | Sample B

---

Of course, sharing math puzzles with your students is just one effective strategy for boosting engagement in your classroom. Subscribe to our mailing list here to get more free daily resources, lesson plans, ideas, and insights for K-12 math teachers in your inbox every week.

Read More Posts About Math Education:

---

By Anthony Persico

Anthony is the lead educator and founder of Mashup Math. He lives in Denver, Colorado and is also a YouTube for Education partner. Follow him on Twitter at @mashupmath.