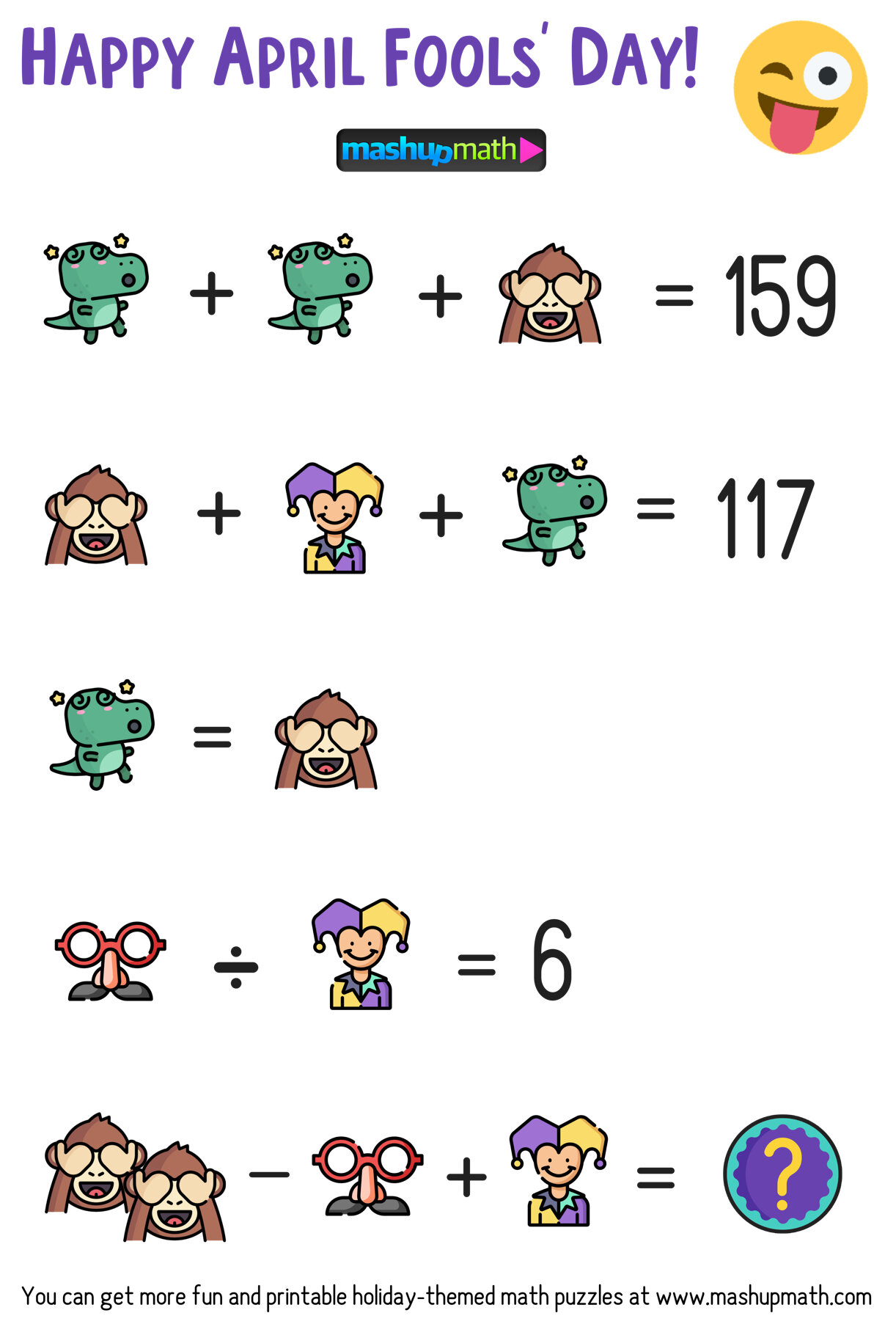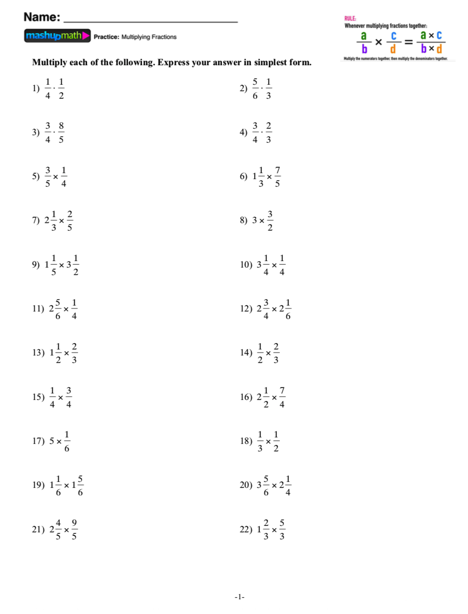April Fools' Day Math Puzzle for Grades 1-6

They’re Here! Are Your Kids Ready for These April Fools’ Day Math Challenges?

April Fools' Day is a perfect time to add a little silliness into your lesson plans.

Whether you’re teaching your kids at home, remotely, or in the classroom, you don’t want to miss this opportunity to make your April 1st math lesson extra special and memorable.

You can start by sharing a few of these 11 Super Cute and Funny Math Jokes and Puns for Kids.

And you can keep the fun going with 3 April Fools’ Day Math Puzzles!

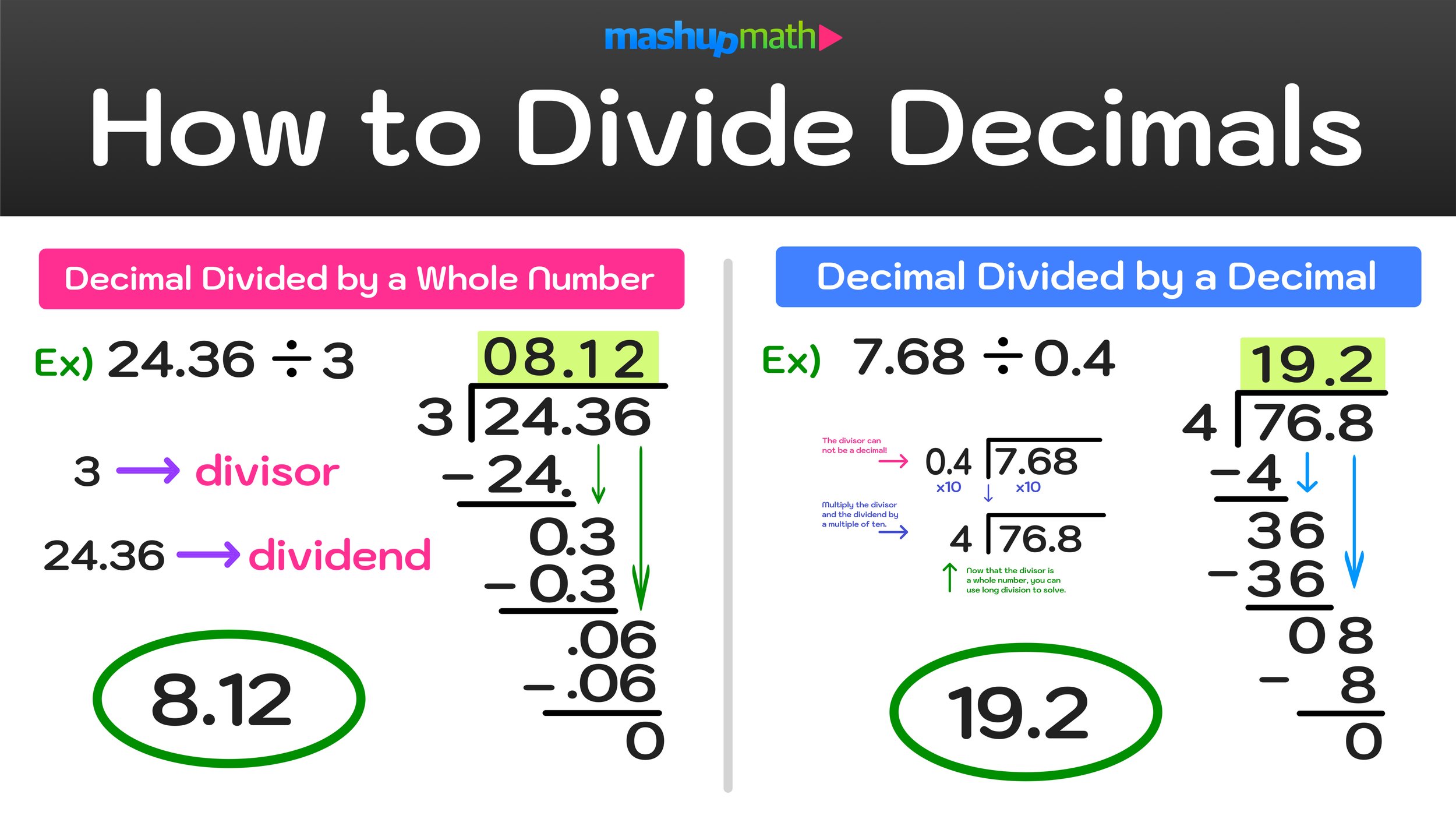
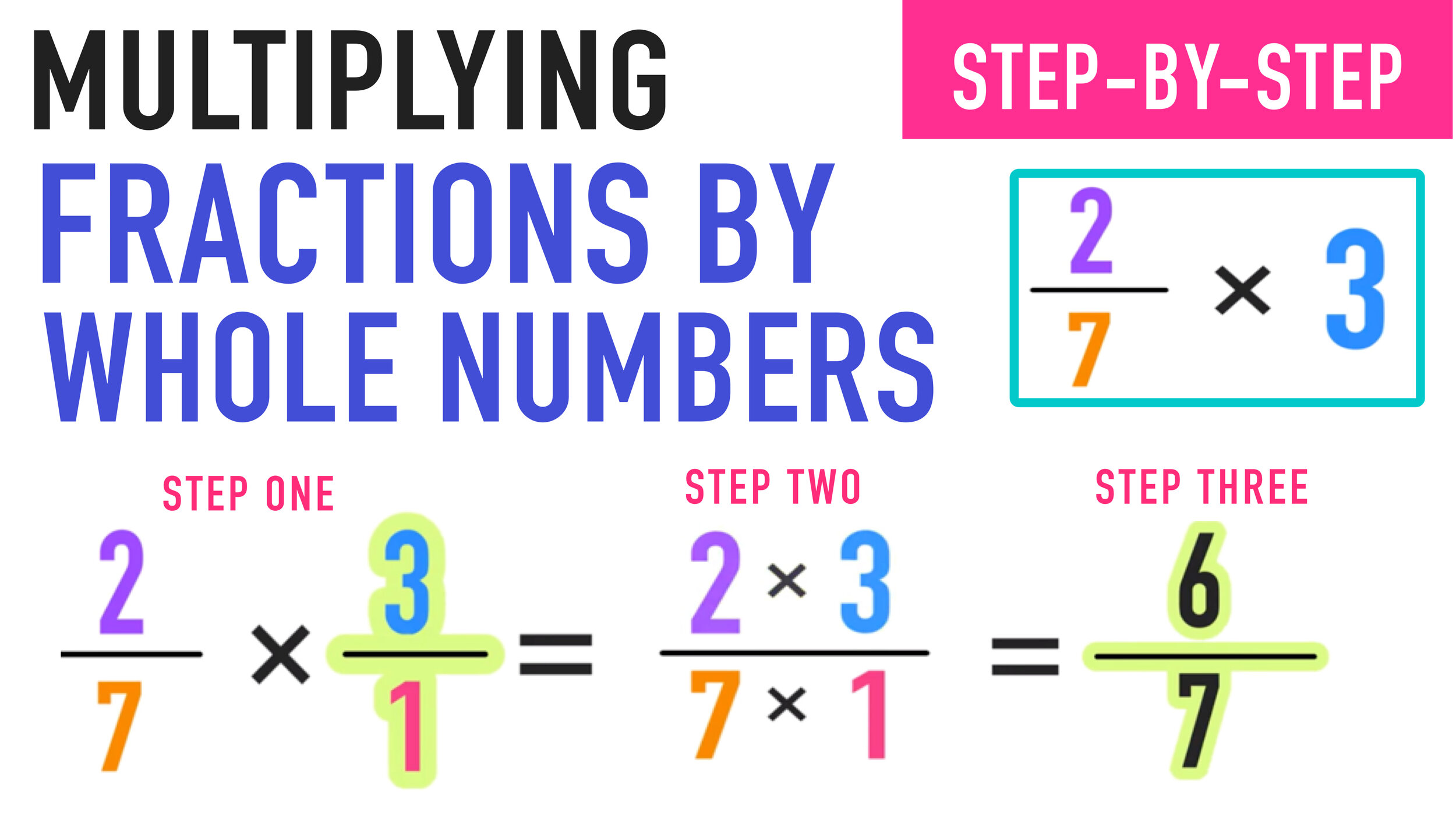
These kinds of activities are best used for warm-ups (anticipatory sets), cooldowns and exit tickets, and transitions. They are especially good for helping your students develop problem-solving skills, mathematical reasoning, and applying the order of operations.

I like to share fun math puzzles like today’s at least once per week to keep my lessons fresh and exciting, and my students love them!

Today’s April Fools’ Day Math Challenges for grades 1-6 are sample puzzles from the best-selling workbook: The Big Book of Super Fun Math Puzzles for Grades 1-6.

The activities are tiered by difficulty using the following system:

Pink Level (Grades 1-2) | Blue Level (Grades 3-4) | Green Level (Grades 5-6+)

April Fools’ Day Math Puzzles for Grade 1 through 6+

Note that:

(answer keys to follow)

Pink Level Puzzle (for Grades 1-2)

Extra Resources: Which One Doesn't Belong? Free Math Activities for Grades 1-8

Blue Level Puzzle (for Grades 3-4)

Free Math Resources: Free Math Coloring Worksheets for 3rd and 4th Grade

Green Level Puzzle (for Grades 5-6+)

Bonus! Would you like over 300 more math puzzles like todays?

Click here to take a closer look at our best-selling The Big Book of Math Puzzles for Students in Grades 1-6 and access more free sample puzzles with answer keys!

And click here to get your copy of The Big Book of Super Fun Math Puzzles for Grades 1-6 as a PDF download.

And here are the answers to the April Fools’ Day Math Puzzles:

Pink Level (Grades 1-2): Jester=5, Disguise=2, Monkey=8, ?=13

Blue Level (Grades 3-4): Jester=10, T-Rex=7, Monkey=5, Disguise=6, ?=84

Green Level (Grades 5-6+): T-Rex=53, Monkey=53, Jester=11, Disguise=66, ?=51

---

Sharing fun math puzzles with your students is just one effective strategy for improving student engagement. Subscribe to our mailing list here to get more free daily resources, lesson plans, ideas, and insights for K-12 math teachers in your inbox every week.

Read More Posts About Math Education:

---

By Anthony Persico

Anthony is the lead educator and founder of Mashup Math. He lives in Denver, Colorado and is also a YouTube for Education partner. Follow him on Twitter at @mashupmath.

Multiplying Fractions by Whole Numbers: Your Complete Guide

Complete Guide: Multiplying Fractions by Whole Numbers

Key Question: How do you multiply fractions and whole numbers?

Learn how to solve these kinds of problems.

Welcome to this free lesson guide where you will learn and easy two-step process for multiplying fractions by whole numbers AND multiplying whole numbers by fractions.

This complete guide to multiplying fractions by whole numbers includes several examples, an animated video mini-lesson, and a free worksheet and answer key.

Let’s get started!

Multiplying Fractions by Whole Numbers: Multiplication Review

Before we explore how to multiply fractions, let’s do a super quick review of how to multiply a fraction by a fraction (understanding how to apply the rule below will make multiplying fractions and whole numbers much easier for you!)

Multiplying Fractions Rule: Whenever multiplying fractions together, multiply the numerators together, then multiply the denominators together as follows…

Example of the Rule:

What is (3/4) x (1/2) ?

Notice that the fraction (3/8) can not be simplified (since 8 and 3 do not have a common divisor)

Answer: (3/4) x (1/2) = 1/8

Looking for More Help With Multiplying a Fraction by a Fraction? Check out this free guide

---

---

How to Multiply a Fraction by a Whole Number (and Vice Versa)

Now that you are familiar with the rule for multiplying a fraction by a fraction, you can use it to help you easily multiply a fraction by a whole number.

Let’s start with an example:

Multiplying Fractions by Whole Numbers: Example 1

Example 1: What is (2/7) x 3 ?

Start by rewriting the whole number (3 in this example) as a fraction, (3/1) as follows…

(You can do this because any number divided by one is always equal to itself)

Now, because you are multiplying a fraction by a fraction, you can apply the rule and solve as follows…

And since (6/7) can not be simplified, you can conclude that:

Answer: (2/7) x 3 = (6/7)

Wait! What would happen if the answer could be simplified? Let’s address the situation in the next example…

---

---

Multiplying Fractions by Whole Numbers: Example 2

Example 1: What is 5 x (9/10) ?

Start by rewriting the whole number (5 in this example) as the fraction (5/1)…

Then apply the rule as follows…

In this example, (45/10) is not the final answer because it can be simplified.

Since the greatest common factor (GCF) of 45 and 10 is 5, you can simplify by dividing both the numerator and the denominator by 5 as follows…

And since (9/2) can not be simplified any further, you can conclude that:

Answer: 5 x (9/10) = (9/2)

Still confused? Check out the animated video lesson below:

---

Video: Multiplying Fractions by Whole Numbers Explained!

Check out the video lesson below to learn more about multiplying fractions and for more free practice problems:

---

Multiplying Fractions by Whole Numbers Worksheets

Free Worksheet!

Are you looking for some extra practice multiplying fractions by whole numbers? Click the links below to download your free worksheets and answer key:

CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET

Tags:  Multiplying Fractions by Whole Numbers, Multiplying Fractions and Whole Numbers, Multiplying Fractions by Whole Numbers Practice, Multiplying Fractions by Whole Numbers Examples, Simplifying Fractions

---

Keep Learning:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Multiplying Fractions: The Complete Guide

Learn to Multiply Fractions by Fractions and by Whole Numbers!

Learning how to multiply fractions, whether it be fraction times fraction or multiplying fractions by whole numbers, is an important skill that every math student must learn at some point.

This complete guide to multiplying fractions will provide a step-by-step tutorial on how to multiply fractions and includes several examples, an animated video mini-lesson, and a free worksheet and answer key.

Let’s get started!

Multiplying Fractions: Multiplication Review

Before we explore how to multiply fractions, let’s do a super quick review of basic multiplication:

Figure A

Figure C

Figure B

Figure D

What do you notice about the relationship between figures A, B, and C?

In figure D, why is 2 x (1/2) equal to 1 ?

Multiplying Fractions Rule

To help you understand Figure D above, let’s start by learning about the rules for multiplying fractions:

Rule: Whenever multiplying fractions together, multiply the numerators together, then multiply the denominators together.

The rules for multiplying fractions are as simple as that, and applying the rule to variety of different problems is just as easy. Let’s go ahead and apply this rule in a few examples.

Multiplying Fractions Examples

Example 1 (Multiplying Fractions by Fractions):

What is (3/4) x (1/2) ?

Start by applying the rule and multiplying the numerators together and then the denominators together as follows:

Notice that the fraction (3/8) can not be simplified (since 8 and 3 do not have a common divisor)

Answer: (3/4) x (1/2) = 3/8

---

---

Example 2 (Multiplying Fractions by Whole Numbers):

What is 2 x (1/2) ?

This problem should look familiar because it’s from Figure D above.

Now that you understand how to use the multiplying fractions rule, you can solve this problem where you have to multiply fractions and whole numbers.

You will still use the rule to find the answer, but there is one extra step involved.

Since you are multiplying fractions by whole numbers, you will need to convert the whole number into a fraction.

In this case, you can rewrite the whole number 2 as (2/1) as follows:

Then apply the rule and solve as follows:

Answer: 2 x (1/2) = 1

Example 3 (Multiplying Fractions and Simplifying Fractions):

What is (5/6) x (3/4) ?

This will be our final example.

This time, you will have to multiply fractions and then simplify your answer.

Start by applying the rule as follows:

Wait! There’s still one more step.

15/24 can simplified because 15 and 24 are both divisible by 3 (which is the GCF of 15 and 24). So you can simplify the fraction by dividing BOTH the numerator and the denominator by 3 as follows:

And that’s all there is to it!

Answer: (5/6) x (3/4) = (5/8)

Still confused? Check out the animated video lesson below:

---

Video: Multiplying Fractions Explained!

Check out the video lesson below to learn more about multiplying fractions and for more free practice problems:

---

Multiplying Fractions Worksheets

Free Worksheet!

Are you looking for some extra practice multiplying fractions? Click the links below to download your free worksheets and answer key:

CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET

Tags:  Multiplying Fractions, Multiplying Fractions and Whole Numbers, Multiplying Fractions Practice, Multiplying Fractions Examples, Simplifying Fractions

---

Keep Learning:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Free Guide: Multiplying Exponents Explained

Multiplying Exponents: The Complete Guide

Are you ready to master the laws of exponents and learn how to Multiply Exponents with the Same Base with ease?

This lesson is part of our Rules of Exponents Series, which also includes the following lesson guides:

• Dividing Exponents

• Working with Fractional Exponents

• Working with Negative Exponents

Let’s start with the following key question about multiplying exponents:

•  How can you multiply powers (or exponents) with the same base?

• Note that the following method for multiplying powers works when the base is either a number or a variable (the following lesson guide will show examples of both)

Multiplying Exponents Example

Let’s start with a simple example: what is 3^3 times by 3^2?

*Notice that each term has the same base, which, in this case is 3.

Start by rewriting each term in expanded form as follows (you won’t have to do this every time, but we’ll do it now to help you understand the rule, which we’ll get to later.)

Since we have 3 being multiplied by itself 5 times ( 3 x 3 x 3 x 3 x 3 ), we can say that the expanded expression is equal to 3^5

And we can conclude that: 3^3 x 3^2 = 3^5

But Why?

Do you notice a relationship between the exponents?

Multiplying Exponents Rule

Did you notice a relationship between all of the exponents in the example above?

Notice that 3^2 multiplied by 3^3 equals 3^5. Also notice that 2 + 3 = 5

This relationship applies to multiply exponents with the same base whether the base is a number or a variable:

Whenever you multiply two or more exponents with the same base, you can simplify by adding the value of the exponents:

Here are a few examples applying the multiplying exponents rule:

Multiplying Exponents Rule Example (Variable Base)

Example: Simplify (X^5)(X^7) ?

Solution: (X^5) (X^7) = X^12 …because 5 + 7 = 12

Multiplying Exponents Rule Example (Numerical Base)

Example: Simplify (8^3)(8^5) ?

Solution: (8^3) (8^5) = 8^8 …because 3 + 5 = 8

Multiplying Powers with the same base is as simple as that!

If you still need help, check out this free Multiplying Exponents video lesson:

Video: Multiplying Exponents Explained in 3 Minutes!

Multiplying Exponents Practice Worksheet and Answer Key

Are you looking for some extra multiplying exponents practice?

Click the link below to download your free Multiplying Exponents Worksheet (PDF) and Answer Key!

>>> Click here to get your free Multiplying Exponents Worksheet.

(answer key included)

Ready to Keep Learning? Here are More Free Related Math Resources:

• How to Convert a Fraction to a Decimal

• Dividing Exponents: The Complete Guide

• Negative Exponent Rule Explained in 3 Easy Steps

• Video Lesson: Scientific Notation Explained

• The Ultimate Guide to Cube Roots

• Free PDF Math Worksheets (with Answers)

• Activity: Here’s an Awesome Way to Teach Kids Fractions

Keep Learning:

---

Share your ideas, questions, and comments below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Free Guide: Dividing Exponents Explained

Dividing Exponents: Everything You Need to Know

Are you ready to become a master of dividing exponents?

(Need help with Negative Exponents, click here for our super easy 3-step explanation)

Let’s start with the following key question about dividing exponents:

•  How can you divide powers (or exponents) with the same base?

• Note that the following method works when the base is either a number or a variable (the following lesson guide will show examples of both)

Dividing Exponents Example

Let’s start with a simple example: what is 5^7 divided by 5^4?

Start by rewriting the fraction in expanded form as follows (you won’t have to do this every time, but we’ll do it now to help you understand the rule, which we’ll get to later.)

Notice how there are repeat values in the numerator and the denominator.

Since any non-zero value divided by itself is equal to one, you can cancel out these repeats as follows:

Doing this allows you to rewrite the above fraction in simplified form, as follows:

Finally, you can rewrite 5 x 5 x 5 as 5^3 and you have finished the problem.

5^7 divided by 5^4 equals 5^3

Dividing Exponents Rule

Did you notice a relationship between all of the exponents in the example above?

Notice that 5^7 divided by 5^4 equals 5^3. Also notice that 7 - 4 = 3

This relationship applies to dividing exponents with the same base whether the base is a number or a variable:

Whenever you divide two exponents with the same base, you can simplify by subtracting the value of the exponent in the denominator by the value of the exponent in the numerator.

Here are a few examples applying the rule:

Dividing Exponents Rule Example (Variable Base)

Dividing Exponents Rule Example (Numerical Base)

Dividing exponents with the same base is as simple as that!

If you still need help, check out this free Dividing Exponents video lesson:

Video: Dividing Exponents Explained in 3 Minutes!

Dividing Exponents Practice Worksheet and Answer Key

Are you looking for some extra dividing exponents practice?

Click the link below to download your free Dividing Exponents PDF Worksheet and Answer Key!

>>> Click here to get your free Dividing Exponents Worksheet.

(answer key included)

Ready to Keep Learning? Here are More Free Related Math Resources:

• How to Convert a Fraction to a Decimal

• Negative Exponent Rule Explained in 3 Easy Steps

• Video Lesson: Scientific Notation Explained

• The Ultimate Guide to Cube Roots

• Free PDF Math Worksheets (with Answers)

• Activity: Here’s an Awesome Way to Teach Kids Fractions

Keep Learning:

---

Share your ideas, questions, and comments below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.