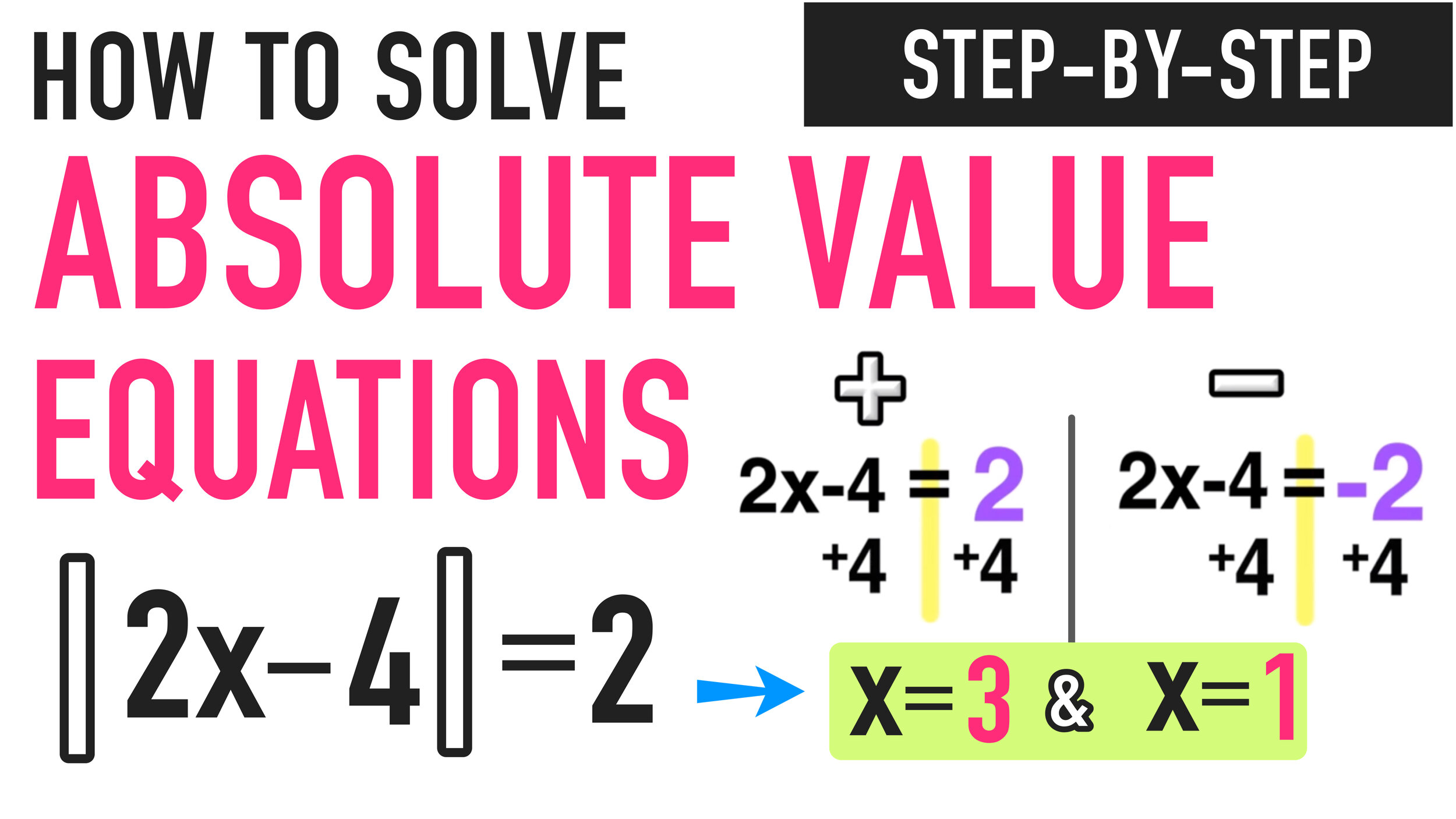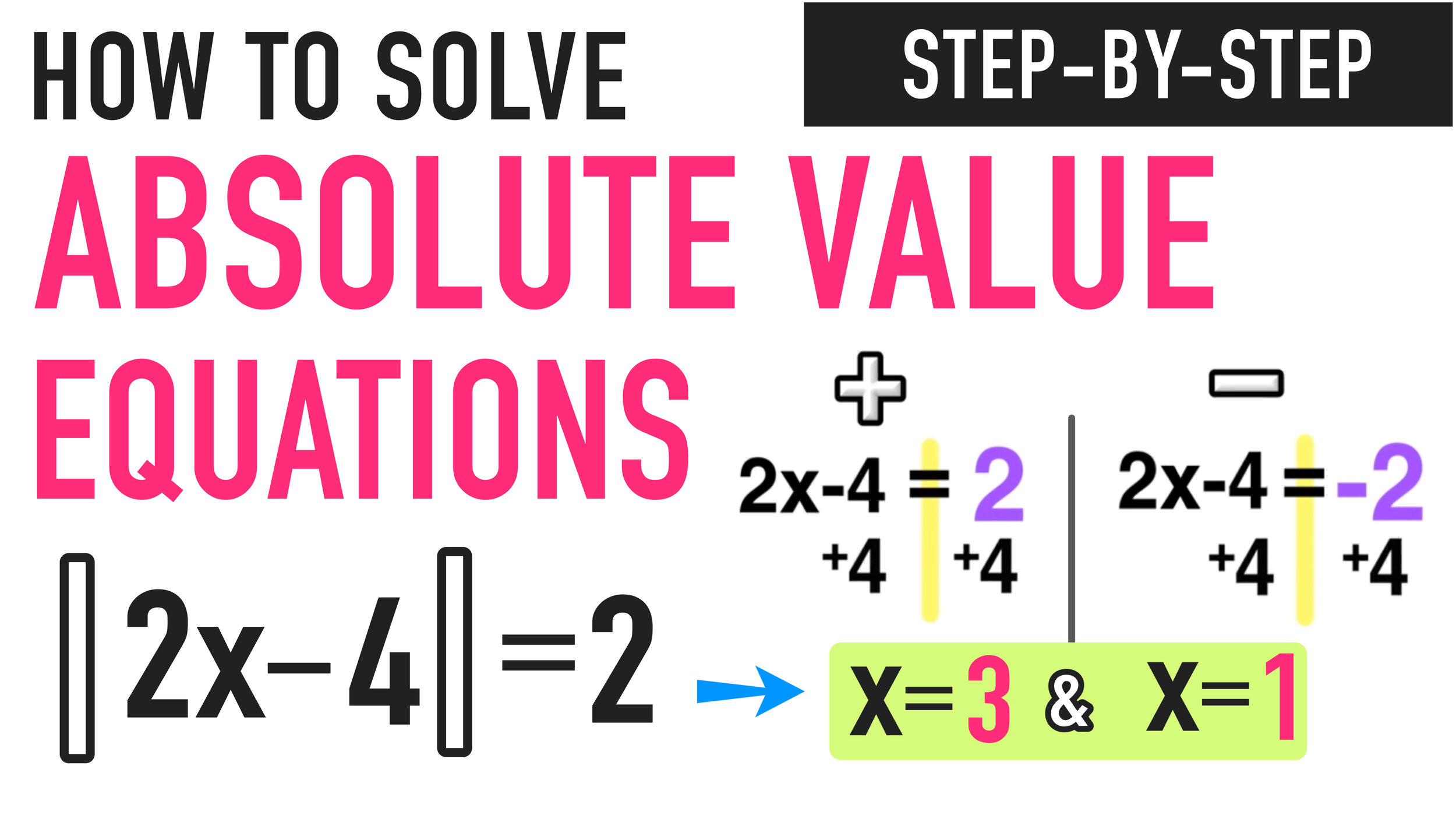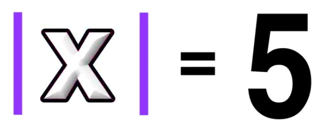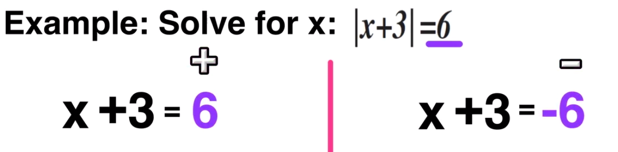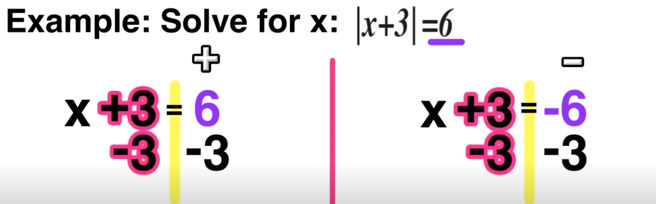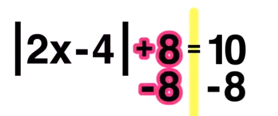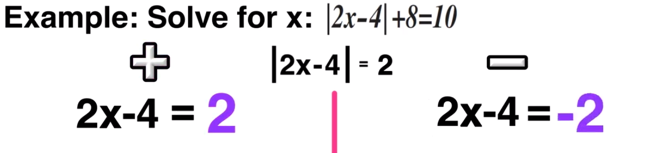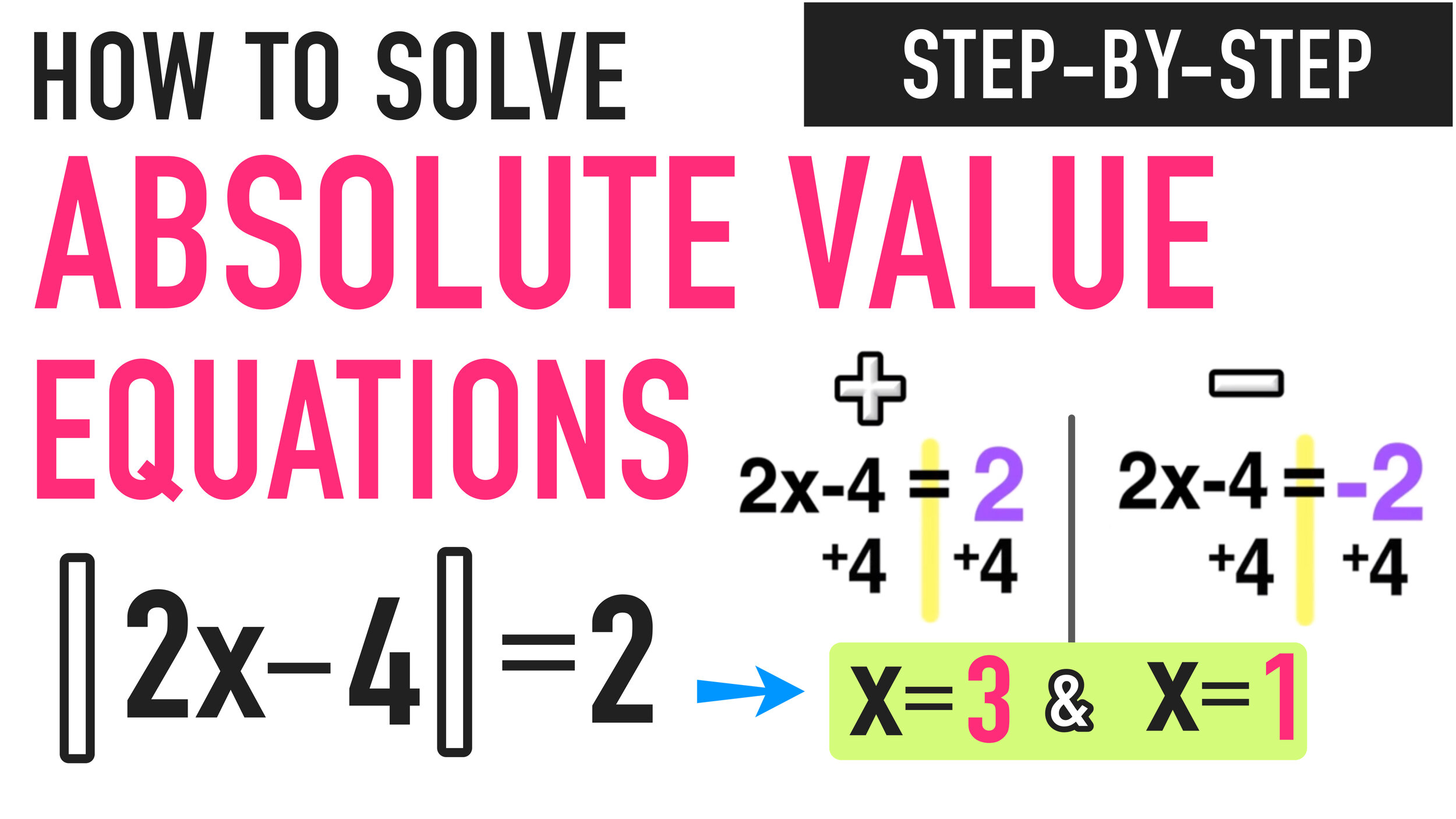Solving Absolute Value Equations: Complete Guide

Learn How to Solve Absolute Value Equations in 3 Easy Steps!

The following step-by-step guide will show you how to solve absolute value equations and absolute value functions with ease (Algebra)

Welcome to this free lesson guide that accompanies this Solving Absolute Value Equations Tutorial where you will learn the answers to the following key questions and information:

• How to solve an absolute value equation

• How to solve an absolute value function

• How to find both solutions to an absolute value equation

• Why is absolute value always positive?

This Complete Guide to Solving Absolute Value Equations includes several examples, a step-by-step tutorial and an animated video tutorial.

---

*This lesson guide accompanies our animated Solving Absolute Value Equations Explained! video.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

Intro to Solving Absolute Value Equations

Before you work on a few absolute value equations examples, let’s quickly review some important information:

Fact: Any value inside of absolute value bars represents either a positive number or zero.

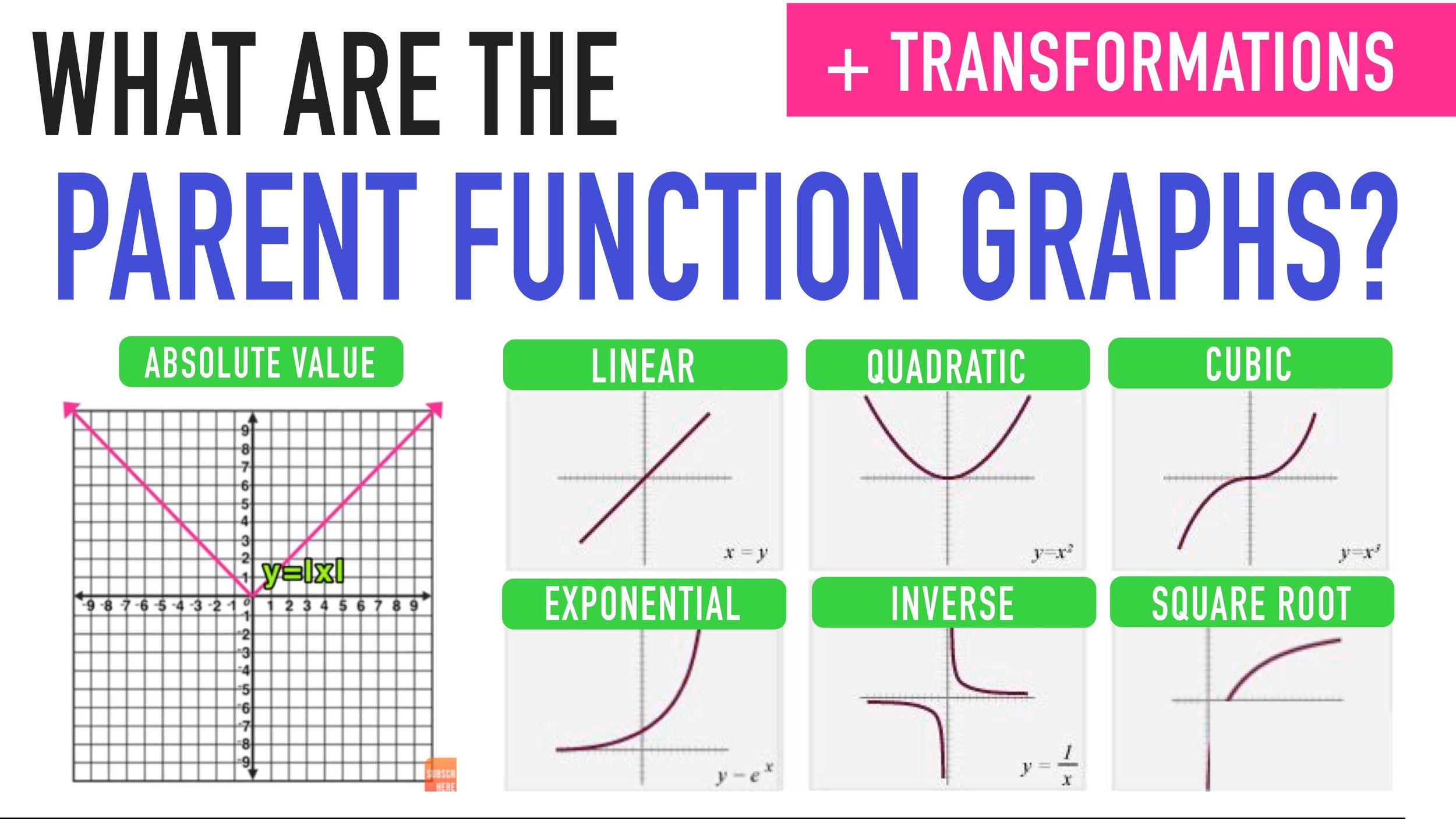
Notice that the absolute value graph in Figure 1 has a range of y is greater than or equal to 0 (it is never negative)

Figure 1: The parent function for absolute value.

Furthermore, consider the example below:

There are two values that would make this equation true!

The absolute value of 5 AND the absolute value of -5 both equal positive 5.

This should make sense when you graph the line y=5 over the absolute value function graph because you can see that there are two intersection points, and thus two solutions.

Absolute value functions can have up to two solutions!

Now you know that ABSOLUTE VALUE EQUATIONS CAN HAVE TWO SOLUTIONS.

Now you are ready to try a few examples.

Solving Absolute Value Equations Example #1

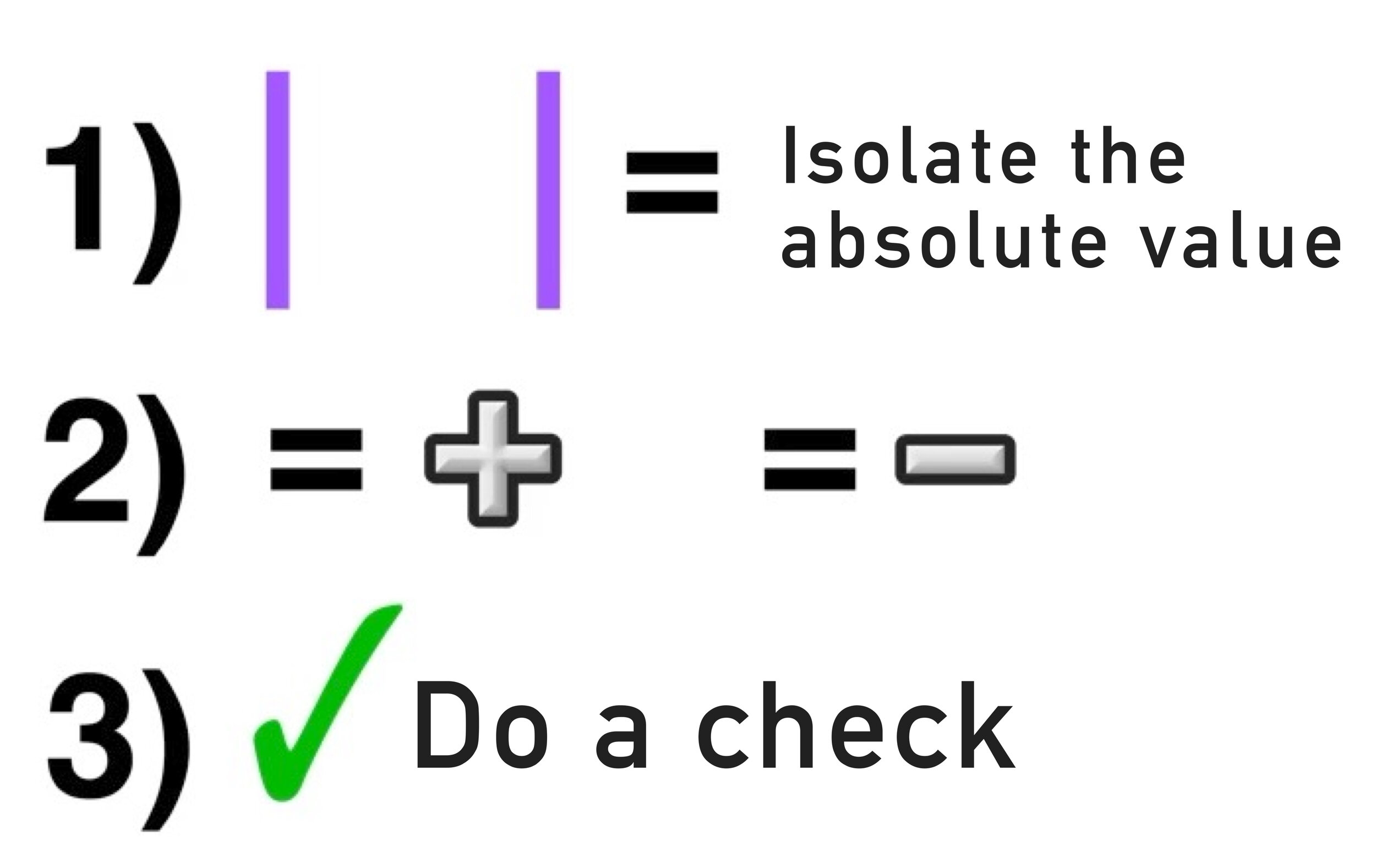
We will be using the following 3-step process that can be used to solve any absolute value equation:

STEP ONE: Isolate the Absolute Value

In this example, the absolute value is already isolated on one side of the equals sign, which means that there are no other terms outside of the absolute value, so you can move onto step two.

STEP TWO: Solve for Positive AND Solve for Negative

For step two, you have to take the original equation |x+3| = 6 and split it up into two equations, one equal to POSITIVE 6 and the other equal to NEGATIVE 6. You also get rid of the absolute value bars.

Set up two equations (positive and negative) and ditch the absolute value bars.

Now you just have to solve each equation for x as follows:

And now you have concluded that there are two solutions to |x+3|=6, x=3 and x=-9.

STEP THREE: Check Your Answer

Finally, do a quick check by plugging both answers into the original equation, |x+3|=6, to make sure that they are correct:

Left: replace x with 3. Right: replace x with -9

Both equations are true.

Since the checks worked out, you can conclude that:

Final Answer: The solutions to |x+3|=6 are x=3 and x=-9

---

---

Solving Absolute Value Equations Example #2

Again, you will follow the three-step process to solving this absolute value equation:

STEP ONE: Isolate the Absolute Value

Unlike the last example, the absolute value is not already isolated on one side of the equal sign, because there is a +8 outside of it that needs to be moved to the other side as follows:

Step One: Isolate the absolute value!

Now the absolute value is isolated.

Now that you have isolated the absolute value on one side of the equal sign, you are ready for the next step.

STEP TWO: Solve for Positive AND Solve for Negative

The next step is to ditch the absolute value bars and solve the following equations:

Positive: 2x-4=2 and Negative: 2x-4=-2

Now you have TWO solutions: x=3 and x=1

STEP THREE: Check Your Answer

The final step is to plug both solutions, x=3 and x=1, into the original equation |2x-4|+8=10 and verify that each solution checks out and you are finished!

Go ahead and check the solution to Example 2 on your own! Did it work out?

---

Still Confused?

Check out this animated video tutorial on solving absolute value equations!

---

---

Looking for more practice with absolute value?

Check out the following free cube root resources:

Free Tutorial

Absolute Value Calculator Basics: How to Graph and Solve Absolute Value Equations

How to Find X and Y Intercepts of a Function Explained!

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

7 Super Fun Math Logic Puzzles for Kids!

7 Super Fun Math Logic Puzzles for Kids Ages 10+ (Answers Included!)

A Post By: Anthony Persico

Working on fun math riddles and brain teasers is a great way for kids to develop number sense and improve their mathematical problem-solving skills.

And these same benefits also apply to math logic puzzles, which also help students learn to think algebraically (usually years before they even step foot inside of an algebra class!).

The following collection of 7 math logic puzzles for kids ages 10+ range from basic to advanced make for a great challenge and a fun math learning experience. Enjoy!

(Looking for more free math puzzles, riddles, and brain teasers for kids?)

---

7 Super Fun Math Logic Puzzles for Kids!

Each of the following math logic puzzles for kids includes an image graphic and there is an answer key at the end!

But if you want more detailed explanations of how to answer every riddle, check out the Math Logic Puzzles Explained! video link below and be sure to give it a thumbs up!

Watch the Math Logic Puzzles Video:

---

Free Worksheet Included!

There is also a link to download a Free Printable PDF Math Logic Puzzles Worksheet and Answer Key that shares all of these logic puzzles at the end of this post!

All of the math logic puzzles below are samples from the best-selling 101 Daily Math Challenges for Engaging Students in Grades 3-8 PDF workbook, which is now available!

7 Super Fun Math Logic Puzzles for Kids:

Math Logic Puzzle #1:

Keep reading to the bottom of this page to see the answer key AND click here to see the video that explains the solution to this problem.

Would you like FREE math resources in your inbox every day? Click here to sign up for my free math education email newsletter (and get a free math eBook too!)

---

Math Logic Puzzle #2:

Keep reading to the bottom of this page to see the answer key AND click here to see the video that explains the solution to this problem.

---

Click here to sign-up for our free weekly email newsletter!

---

Math Logic Puzzle #3:

Keep reading to the bottom of this page to see the answer key AND click here to see the video that explains the solution to this problem.

---

Are you looking for more super fun Math Riddles, Puzzles, and Brain Teasers to share with your kids?

The best-selling workbook 101 Math Riddles, Puzzles, and Brain Teasers for Kids Ages 10+! is now available as a PDF download. You can get yours today by clicking here.

---

Math Logic Puzzle #4:

Keep reading to the bottom of this page to see the answer key AND click here to see the video that explains the solution to this problem.

---

Math Logic Puzzle #5:

Keep reading to the bottom of this page to see the answer key AND click here to see the video that explains the solution to this problem.

---

Math Logic Puzzle #6:

Keep reading to the bottom of this page to see the answer key AND click here to see the video that explains the solution to this problem.

---

Math Logic Puzzle #7:

Keep reading to the bottom of this page to see the answer key AND click here to see the video that explains the solution to this problem.

---

Math Logic Puzzle Bonus!

---

---

ANSWER KEY:

1. Peach=8, Watermelon=12, Banana=5

2. Planet=7, Helmet=4, Rocket=11

3. Yellow Pot=17, Orange Pot=0, Purple Pot=17

4. Burger=25, Ketchup=8, French Fries=25

5. Playstation Controller=6, Gameboy=3, Switch Controller=18

6. Husky=10, Terrier=17, Poodle=10

7. Cake=5, Cookie=40, Cupcake=6

   Bonus: Van=12, Dove=0, Heart=6

Free PDF Worksheet:

Click here to get your Free Math Riddles PDF Worksheet and Answer Key!

And click here to sign up for our math education mailing list to start getting free K-12 math activities, puzzles, and lesson plans in your inbox every week!

Are you looking for more super fun Math Puzzles to share with your kids?

My best-selling workbook 101 Daily Math Challenges for Engaging Students in Grades 3-8 is now available as a PDF download. You can get yours today by clicking here.

---

Did I miss your favorite math riddle for kids? Share your thoughts, questions, and suggestions in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math and an advisor to Amazon Education's 'With Math I Can' Campaign. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

You Might Also Like…

Complete Guide to Graphing Cubic Functions and Cube Root Graphs

How to Graph Cubic Functions and Cube Root Graphs

The following step-by-step guide will show you how to graph cubic functions and cube root graphs using tables or equations (Algebra)

Welcome to this free lesson guide that accompanies this Graphing Cube Root Functions Tutorial where you will learn the answers to the following key questions and information:

• How can I graph a cubic function?

• How can I graph a cube root function?

• How can I graph a cubic function equation?

• How can I graph a function over a restricted domain?

This Complete Guide to Graphing Cubic Functions includes several examples, a step-by-step tutorial and an animated video tutorial.

---

*This lesson guide accompanies our animated Graphing Cubic Functions Explained! video.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

Example: Graphing a Cube Root Function

On this example, you will be graphing the function over a restricted domain, but the method we use will work graphing any cubic function.

Example:

Since you are graphing this function over a restricted domain, you only care about graphing how the function behaves between -6 and 10.

Start by building a table that you can use to help yourself find the value of the y-coordinates for all of the x-values from -6 to 10 as follows:

Now you are ready to start finding points on the graph. Let’s start by finding the y-value when x=-6 (the first point on the table).

Plug each x-value into the function and solve for y!

To find the value of y when x=-6, just plug -6 in for x into the original function and solve as follows:

The cube root of -8 is -2.

Since the cube root of -8 is -2, you can conclude that when x=-6, y=-2, and you know that the point (-6,-2) is on the graph of this cubic function!

(-6,-2) is one of the points this function passes through!

You can find the rest of the y-values on the table by either:

A.) Repeating the above process for each x-value

or

B.) Using your graphing calculator to input the function into y= and generating the table as follows:

---

After you fill out your table, you’ll notice that some coordinate points are both integers, while others are decimals:

To graph the function, you will only plot the points that are integers only (this way, you won’t have to estimate where the decimal points lay on the graph)

Now you can go ahead and plot the following points on the graph:

(-6,-2), (1,-1), (2,0), (3,1), (10,2)

The last step is to connect the points with a curved line as follows:

This is the graph of the cubic function over the restricted domain!

You can also use your graphing calculator to verify that your graph is correct.

That’s all there is to it!

---

Still Confused?

Check out this animated video tutorial on graphing cubic functions!

---

---

Looking for more practice with cube roots?

Check out the following free cube root resources:

Free Cube Root Reference Guide

What is the Cube Root of…? Reference Guide

What is the Cube Root Parent Function?

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Complete Guide to Multiplying Binomials: Foil Method and Box Method

Multiplying Binomials Using the Box Method Area Model and Foil Math Lesson

The following step-by-step guide will show you easy strategies for multiplying binomials including the foil method

Welcome to this free lesson guide that accompanies this Multiplying Binomials Tutorial where you will learn the answers to the following key questions and information:

• How can I multiply binomials using the foil method?

• How can I multiply binomials using the box method?

• How can I multiply binomials using the area model method?

• How can I multiply binomials using the distributive method?

This Complete Guide to Multiplying Binomials includes several examples, a step-by-step tutorial, an animated video mini-lesson, and a free multiplying binomials worksheet and answer key.

---

*This lesson guide accompanies our animated Multiplying Binomials Explained! video.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

Example 1: Multiplying Binomials Using the Box Method

The box method for multiplying binomials is also known as the area model method.

Example: Write the following in expanded form

To use the area model method or box method for multiplying binomials, start by drawing a 4x4 box.

The write the terms of the first binomial ( (x-5) in this example) along the top row and the terms of the second binomial ( (6x+12) in this example) along the left column of the box as follows:

Next, multiply the terms of each corresponding column and row (like a bingo board) as follows:

Now you four terms: 6x^2, -30x, 12x, and -60

Notice that -30x and 12 are like terms.

The final step is to combine like terms (-30x + 12x = -18x) and write your answer in expanded form as follows:

Answer: 6x^2 -18x -60

---

---

Example 2: Multiplying Binomials Using the Foil Method

The foul math method is the most common strategy for multiplying binomials. You can use it as an alternative to the box method.

Example: Write the following in expanded form

To multiply binomials using FOIL, you must follow these steps:

Note that FOIL is an acronym that stands for FIRST-OUTER-INNER-LAST

FIRST: Multiply the first terms of each binomial together. In this case: 8 x 8 = 64

OUTER: Multiply the outer terms of each binomial together. In this case: 8 x -5x = -40x

INNER: Multiply the inner terms of each binomial together. In this case: -5x x 8 = -40x

LAST: Multiply the last terms of each binomial together. In this case: -5x x -5x = +25x^2

Now you have four terms: 64, -40x, -40x, and 25x^2

Notice that there are two like terms that can be combined as follows:

The final step is to rearrange the above expression into ax^2 + bx + c form

Answer: 25x^2 -80x +64

---

Still Confused?

Check out this animated video tutorial on multiplying binomials using the box method and foil method (and the distributive method too!)

---

---

Extra Practice: Free Multiplying Binomials Worksheet

Free Worksheet!

Are you looking for some extra practice? Click the links below to download your free worksheets and answer key:

Multiplying Binomials Practice Worksheet:

CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Using the Arc Length Formula and Sector Area Formula: Complete Guide

How to Solve Problems Using the Arc Length Formula and Sector Area Formula

The following step-by-step guide will show you how to use formulas to find the arc length and area of a sector (Algebra, Geometry, Calculus)

Welcome to this free lesson guide that accompanies this Arc Length and Sector Area Explained! Tutorial where you will learn the answers to the following key questions and information:

• What is the arc length formula? What is the arc length equation?

• What is the sector area formula? What is the sector area equation?

• How can I find the length of an arc of a circle?

• How can I find the area of a sector of a circle?

This Complete Guide to Arc Length and Sector Area includes several examples, a step-by-step tutorial, an animated video mini-lesson, and a free equation of a circle worksheet and answer key.

---

*This lesson guide accompanies our animated Arc Length and Sector Area Explained! video.

Want more free math lesson guides and videos? Subscribe to our channel for free!

---

How to Use the Arc Length Formula and the Sector Area Formula:

Before you learn the arc length equation and the area of a sector equation, let’s quickly review two very important (and very familiar) circle properties: Circumference and Area

The circumference of a circle is the linear distance around the circle, or the length of the circle if it were opened up and turned into a straight line.

The area of a circle is the number of square units it takes to fill up the inside of the circle.

Note the circumference and area apply to the entire circle.

In the case of arc length and sector area, you will only be dealing with a portion of a circle.

The Arc Length Formula:

What if you only want to find the length of a portion of the outside of a circle and not the entire circumference?

Whenever you want to find the length of an arc of a circle (a portion of the circumference), you will use the arc length formula:

Where θ equals the measure of the central angle that intercepts the arc and r equals the length of the radius.

The Sector Area Formula:

What if you only want to find the area of a portion of a circle (a sector) and not the entire area?

Whenever you want to find area of a sector of a circle (a portion of the area), you will use the sector area formula:

Where θ equals the measure of the central angle that intercepts the arc and r equals the length of the radius.

Now that you know the formulas and what they are used for, let’s work through some example problems!

Using the Arc Length Formula Practice Problem

Example: Find the length of arc KL

Notice that this question is asking you to find the length of an arc, so you will have to use the Arc Length Formula to solve it!

Before you can use the Arc Length Formula, you will have to find the value of θ (the central angle that intercepts arc KL) and the length of the radius of circle P.

You know that θ = 120 since it is given that angle KPL equals 120 degrees. And, since you know that diameter JL equals 24cm, that the radius (half the length of the diameter) equals 12 cm.

So θ = 120 and r = 12

θ = 120 and r = 12

Now that you know the value of θ and r, you can substitute those values into the Arc Length Formula and solve as follows:

Replace θ with 120.

Replace r with 12.

Simplify the numerator.

1440/180 equals 8.

Answer: The length of Arc KL is approximately 25.1cm (and 8π if you want to leave your answer in terms of pi).

---

---

Using the Sector Area Formula Practice Problem

Example: Find the area of a sector a circle K

Notice that this question is asking you to find the area of a sector of circle K, so you will have to use the Sector Area Formula to solve it!

Before you can use the Sector Area Formula, you will have to find the value of θ (the central angle that intercepts arc AB, which is the arc of the shaded region) and the length of the radius of circle K.

You already know that the radius r is equal to 5. But what about θ ?

∠AKB and ∠AKC are supplementary

In this example, θ is the measure of angle ∠AKB, (the central angle of the green region), but the question only tells you that ∠AKC = 117 degrees.

Since ∠AKB and ∠AKC are supplementary, they have a sum of 180 degrees. You can find the measure of ∠AKB as follows:

θ = ∠AKB = 180 - 117 = 63 degrees.

So θ = 63 and r = 5

Now that you know the value of θ and r, you can substitute those values into the Sector Area Formula and solve as follows:

Replace θ with 63.

Replace r with 5.

r^2 equals 5^2 = 25 in this example.

Simplify the numerator, then divide.

Answer: The area of the green sector is approximately 4.4 square cm (and (35/8)π if you want to leave your answer in terms of pi).

---

---

Arc Length and Sector Area Formulas: Video Tutorial

Still confused? Check out the animated video lesson below:

Check out the video lesson below to learn more about the arc length and sector area formulas and to see more completing the square problems solved step-by-step:

Arc Length and Sector Area Word Problems (Advanced Practice)

Looking for more advanced practice with arc length and sector area? The following video lesson covers topics including:

• arc length and sector area word problems

• using the arc length and sector area equations to solve real-world problems

---

Extra Practice: Free Arc Length and Sector Area Worksheet

Free Worksheet!

Are you looking for some extra practice? Click the links below to download your free worksheets and answer key:

Arc Length and Sector Area Worksheet:

CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET

Keep Learning with More Free Lesson Guides:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.