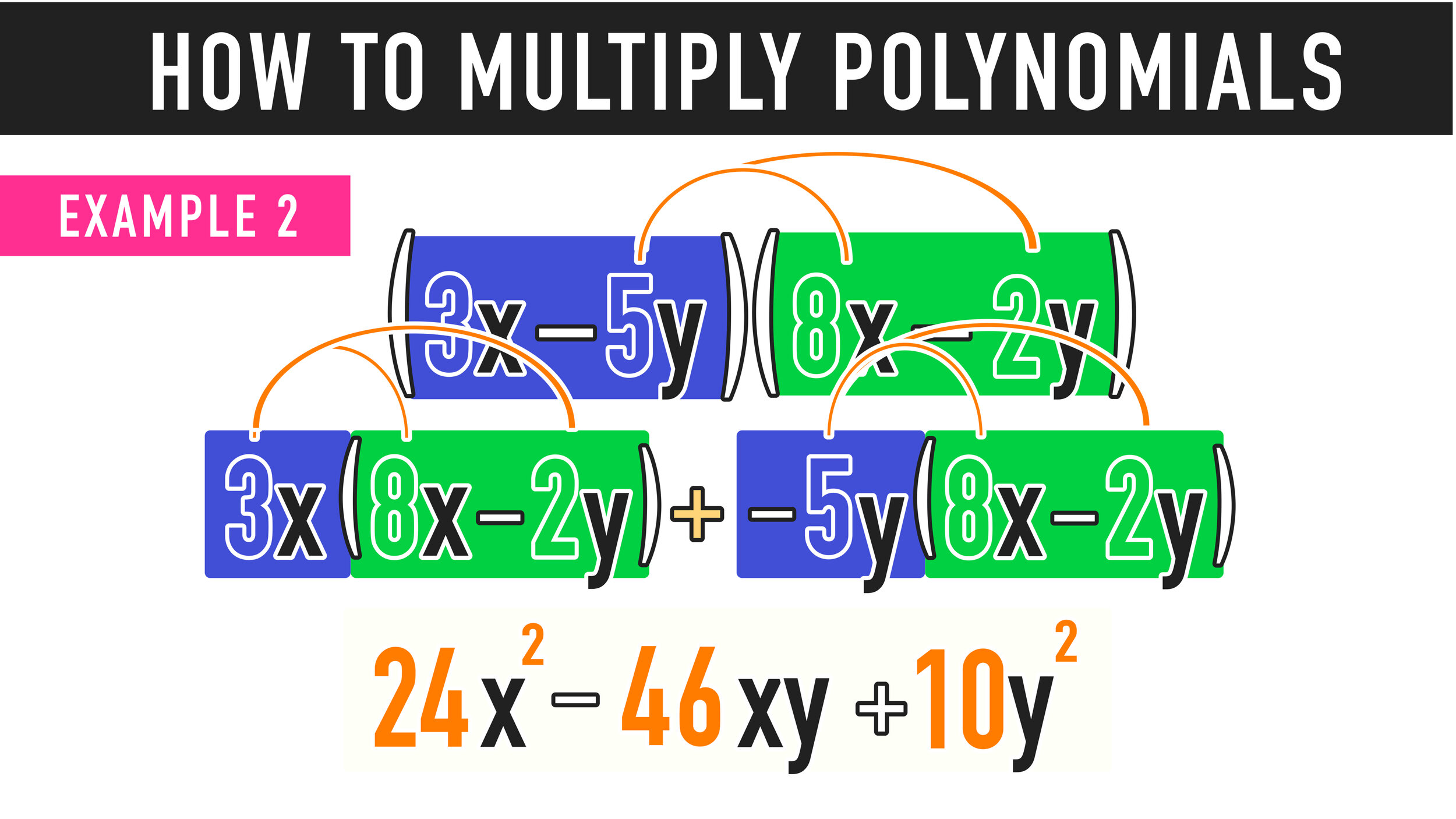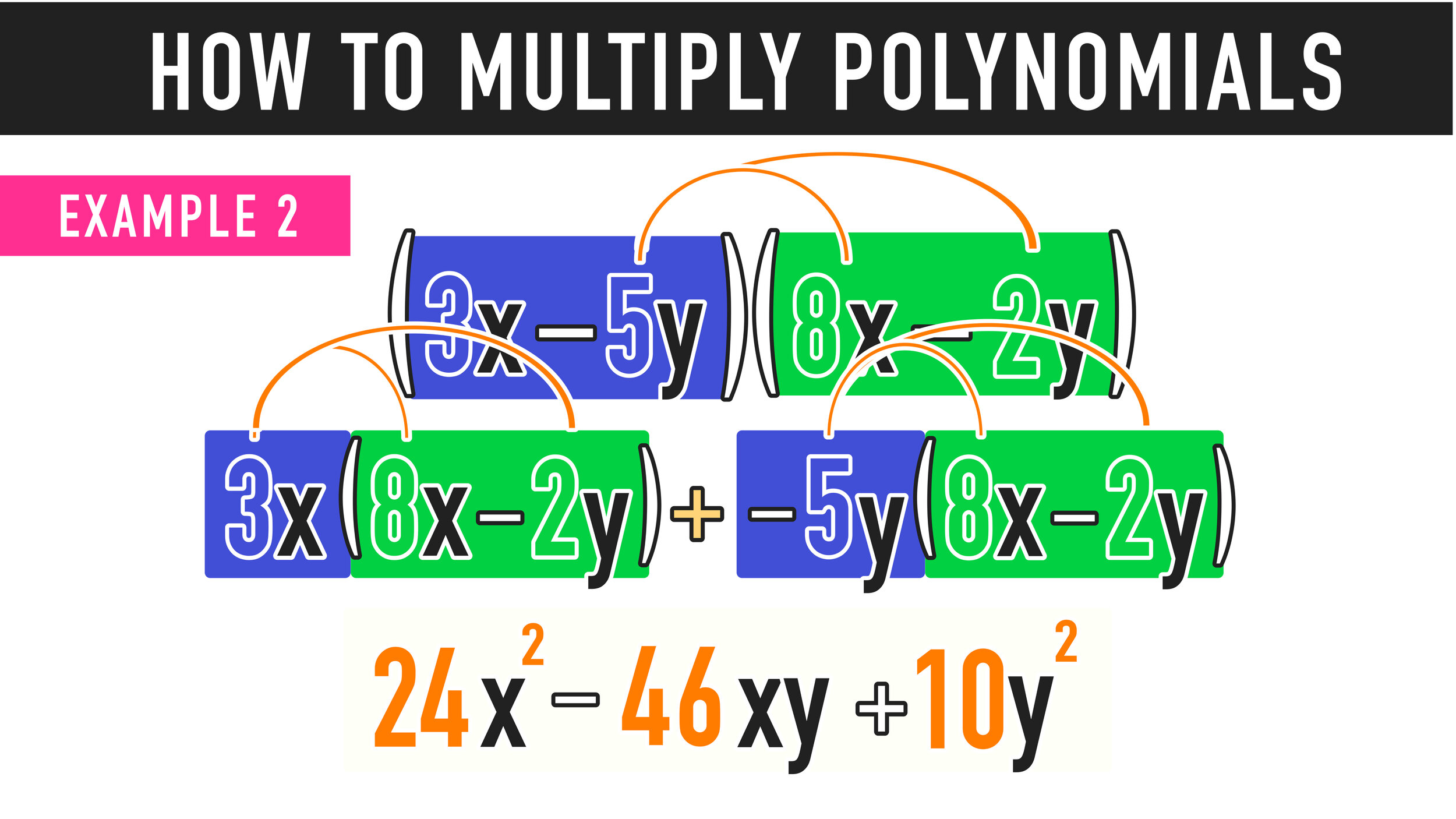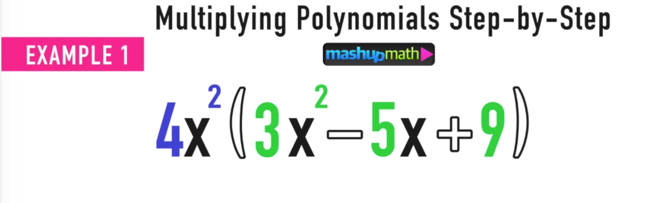The Best Method for Multiplying Polynomials
The following step-by-step guide will show you how to multiply polynomials using the distributive method and includes 3 examples!
Welcome to this free lesson guide that accompanies this Multiplying Polynomials Made Easy! video tutorial where you will learn the answers to the following key questions and information:
What is the best method for multiplying polynomials?
How to perform multiplication of polynomials
Multiplication of monomials, binomials, and trinomials
Multiplying Polynomials Using the Distributive Property
This Complete Guide to Multiplying Polynomials includes several examples, a step-by-step tutorial and an animated video tutorial.
*This lesson guide accompanies our animated Multiplying Polynomials Made Easy! video.
Want more free math lesson guides and videos? Subscribe to our channel for free!
Multiplying Polynomials Explained!
Before you learn how to multiply polynomials, let’s quickly review some important information:
The Distributive Property
Definition: The distributive property allows for you to multiply a sum by multiplying each term separately and then add all of the products together.
If you understand the distributive property, you will be able to multiply polynomials with ease.
Multiplying Polynomials Examples
Multiplying Polynomials Example 1: Multiplying by a Monomial
In this first example, you will be multiplying a monomial by a trinomial. You can think of this as multiplying one “thing” by “another thing” as follows:
This is where using the distributive property (or distributive method) will help you!
To multiply these polynomials, start by taking the first polynomial (the purple monomial) and multiplying it by each term in the second polynomial (the green trinomial).
This can be done by multiplying 4x^2 by the first term of the green trinomial (Figure 1), then by the second term of the green trinomial (Figure 2) and finally by the third term of the green trinomial (Figure 3).
Figure 1
Figure 2
Figure 3
The next step is to simplify each of these new terms and find their sum:
Simplify the first term.
Simplify the second term.
Simplify the third term.
The final step is to check and see if you can COMBINE LIKE TERMS. In this example, there are no like terms, so you can conclude that:
Final Answer:
Figure 2
Multiplying Polynomials Example 2: Multiplying Binomials
You can use the distributive method for multiplying polynomials just like the last example!
Start by multiplying the first term of the first binomial (3x) by the entire second binomial (Figure 1).
Then multiply the second term of the first binomial (-5y) by the entire second binomial (Figure 2).
Figure 1
Figure 2
The next step is to use the distributive property again to simplify each new term.
Note that you do not need the plus sign between -6xy and -40xy.
The final step is to COMBINE LIKE TERMS and simplify:
Final Answer:
Multiplying Polynomials Example 3: Multiply a Binomial by a Trinomial
Figure 1
Remember that you are still just multiplying two things together! And you can do that by using the distributive method again as follows:
Now you can use the distributive method again to simplify the new terms:
The final step is to COMBINE LIKE TERMS and simplify:
-42x^2 and -27x^2 combine to make -69x^2
+14x and +54x combine to make +68x
Now that you have combined like terms, you can conclude that:
Final Answer:
Still Confused?
Check out this animated video tutorial on multiplying polynomials:
Looking for more practice with multiplying polynomials?
Check out the following free resources:
Free Tutorial
Multiplying Binomials Using the Box Method: Complete Guide
Multiplying Binomials Using FOIL Method: Complete Guide
Keep Learning with More Free Lesson Guides:
Have thoughts? Share your thoughts in the comments section below!
(Never miss a Mashup Math blog--click here to get our weekly newsletter!)
By Anthony Persico
Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.