Where is the hundredths place value in math?

Where is the hundredths decimal place in math?

In math, when we look at numbers, we can assign something called place value to each digit based on the position of each number.

When learning about and analyzing numbers—ranging from simple single-digit numbers all the way up to extremely large numbers that can have ten digits or more or—it is important that you understand the meaning of the significance of each digit’s place value, especially when decimals are involved.

When you first start learning about place value, determining each digit’s place value can be simple, especially when you are dealing with integers and decimals are not involved. However, once decimals are in play, identifying place value can get a bit trickier.

This free and simple guide for students will focus on the hundredths place and can be used as a quick review to help you along your place value journey when you start working with numbers involving decimals.

Once you understand place value, you will gain a deeper understanding of numbers—large and small—and your mental math and operational skills (performing addition, subtraction, multiplication, division, and more) will surely improve.

Are you ready to get started?

What is place value?

Before we learn about the hundredths place and what it means in terms of place value, let’s do a super quick review of some key vocabulary terms and some things that you may already know.

Definition: In math, place value refers to the numerical value that a digit has by virtue of its position in the number.

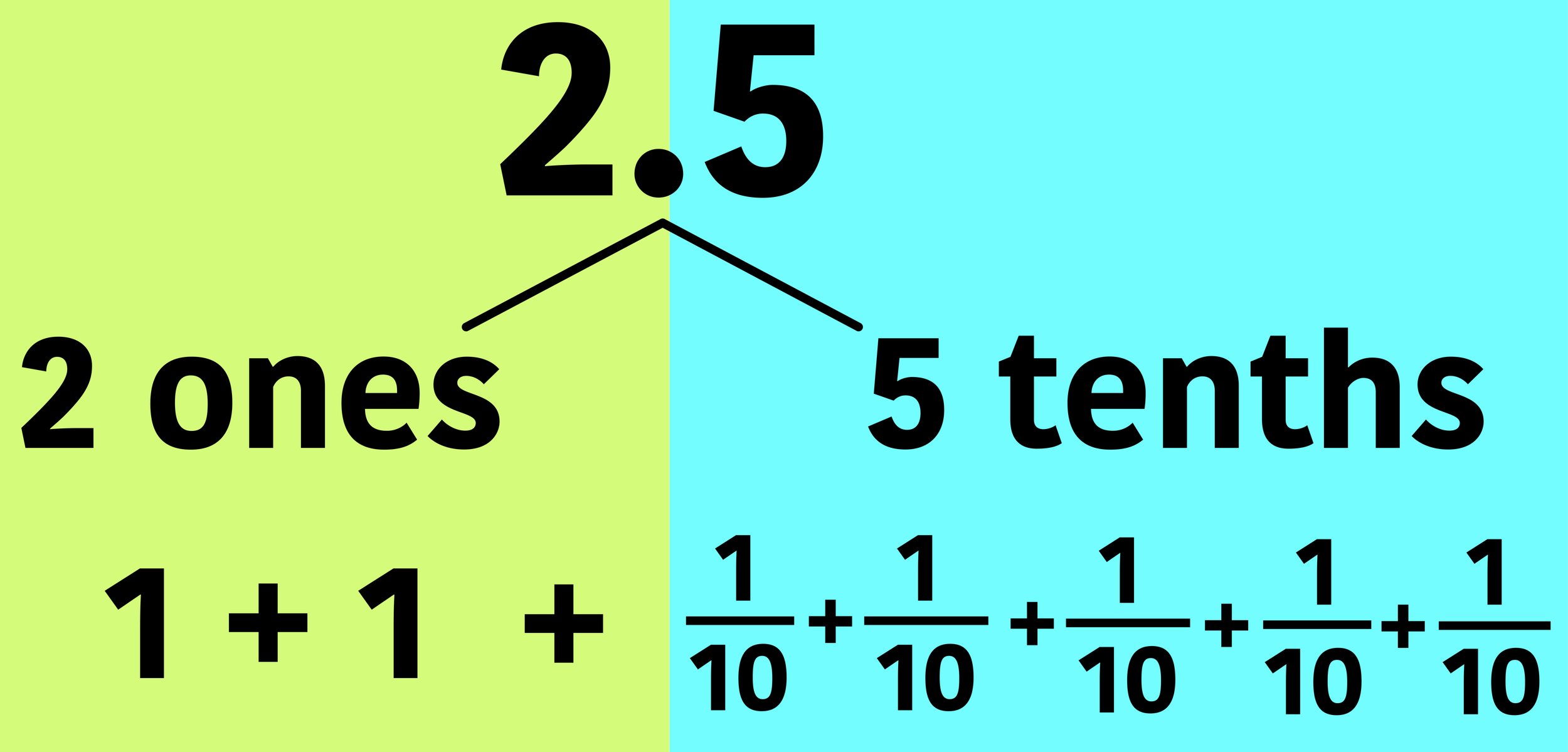
For example, consider the number 2.5.

We can think of the number 2.5 as the sum of 2 ones and 5 tenths.

So, in terms of place value, we can say that for the number 2.5:

•  2 is in the ones place

• 5 is in the tenths place

Pretty simple, right? Now, let’s extend this understanding of place value to the hundredths place.

 What is the hundredths place?

In our last example, we looked at 2.5, which is a relatively simple decimal. As numbers grow larger, you will have to identify larger types of place values.

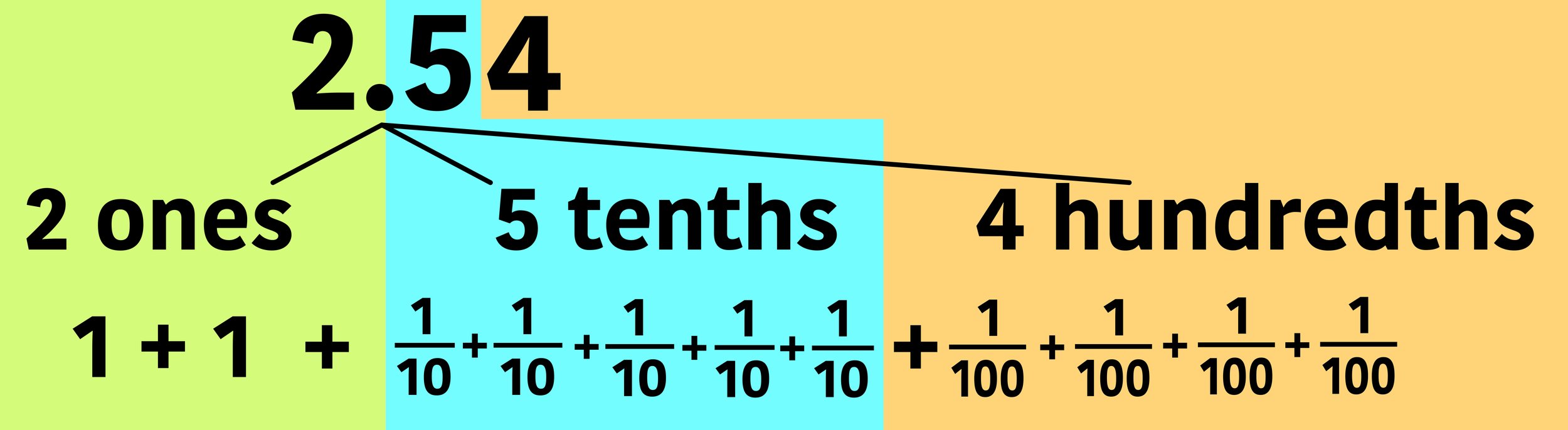
For example, consider the number 2.54.

We can express the number 2.54 as the sum of 2 ones, 5 tenths, and 4 hundredths.

So, in terms of place value, we can say that for the number 2.54:

•  2 is in the ones place

• 5 is in the tenths place

• 4 is in the hundredths place

In these previous examples, we are essentially deconstructing each number to identify the place value of each digit.

Note that the tenths place is different than the tens place and the hundredths place is different than the hundreds place.

 The chart below shows you each place value position relative to a decimal point.

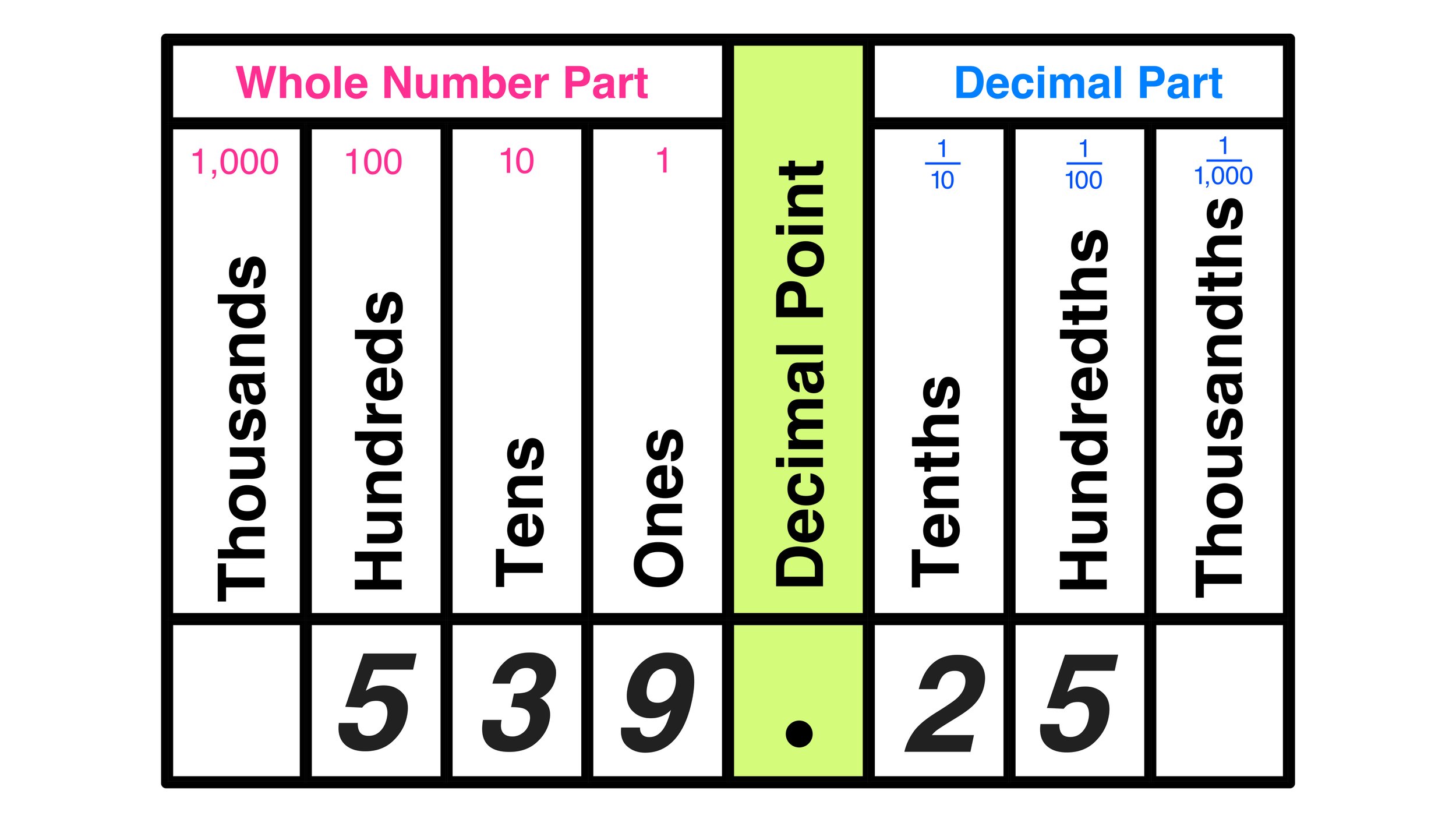
For example, consider the number 539.25

We can insert this value into the chart as follows:

Using the chart, we can clearly see that

• 5 is in the hundreds place

• 3 is in the tens place

• 9 is in the ones place

• 2 is in the tenths place

• 5 is in the hundredths place

 Be sure not to confuse the hundreds place with the hundredths place!

Hundredths Decimal Place Examples

Now let’s go ahead and look at some more examples of determining which number is in the hundredths decimal place of a given number.

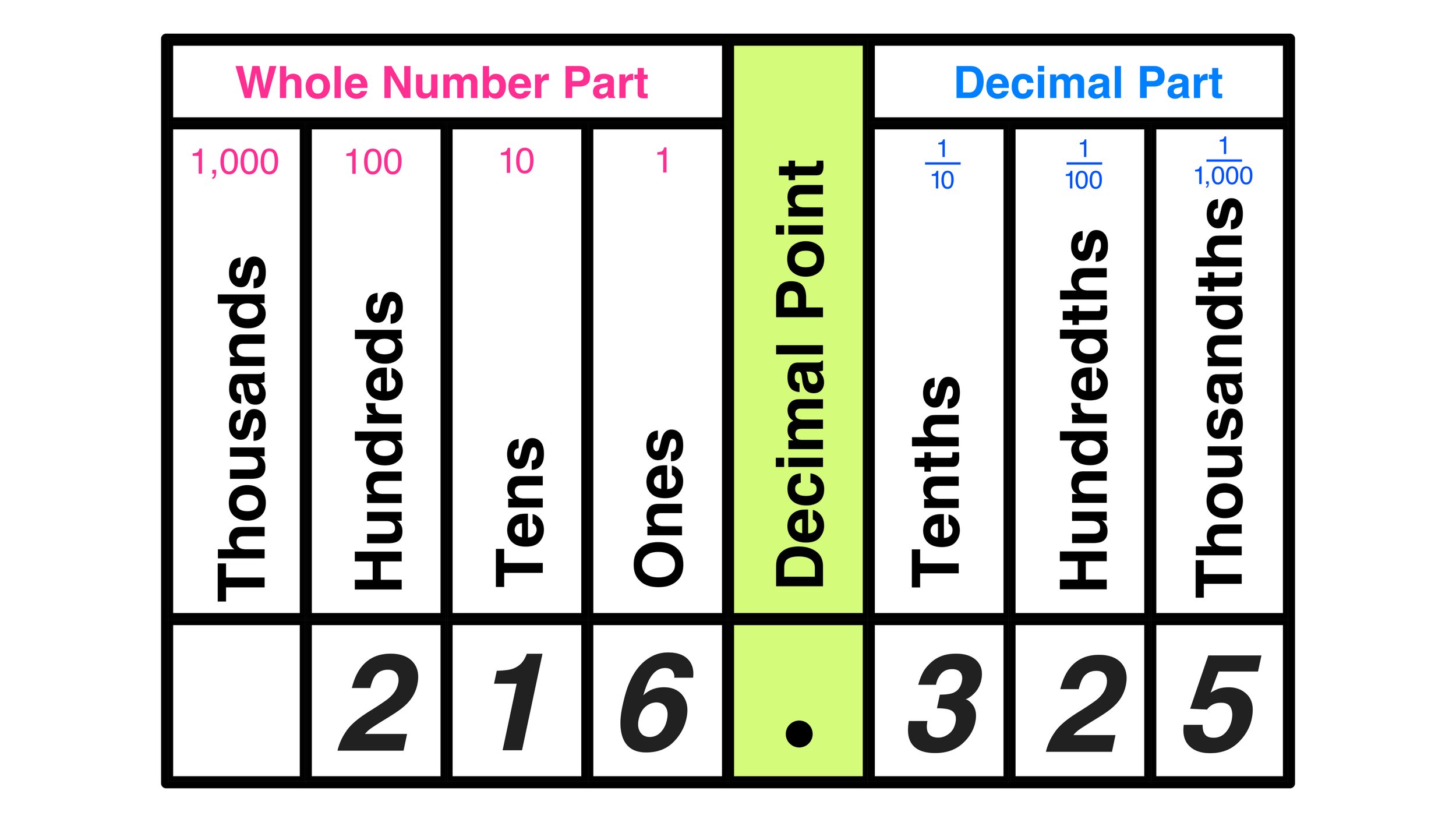
Example #1: Which digit is in the hundredths decimal place?

216.325

 We can input this value into our chart as follows.

Using the chart, it is easy to see that the value in the hundredths place is 2.

 216.325

 Answer: 2

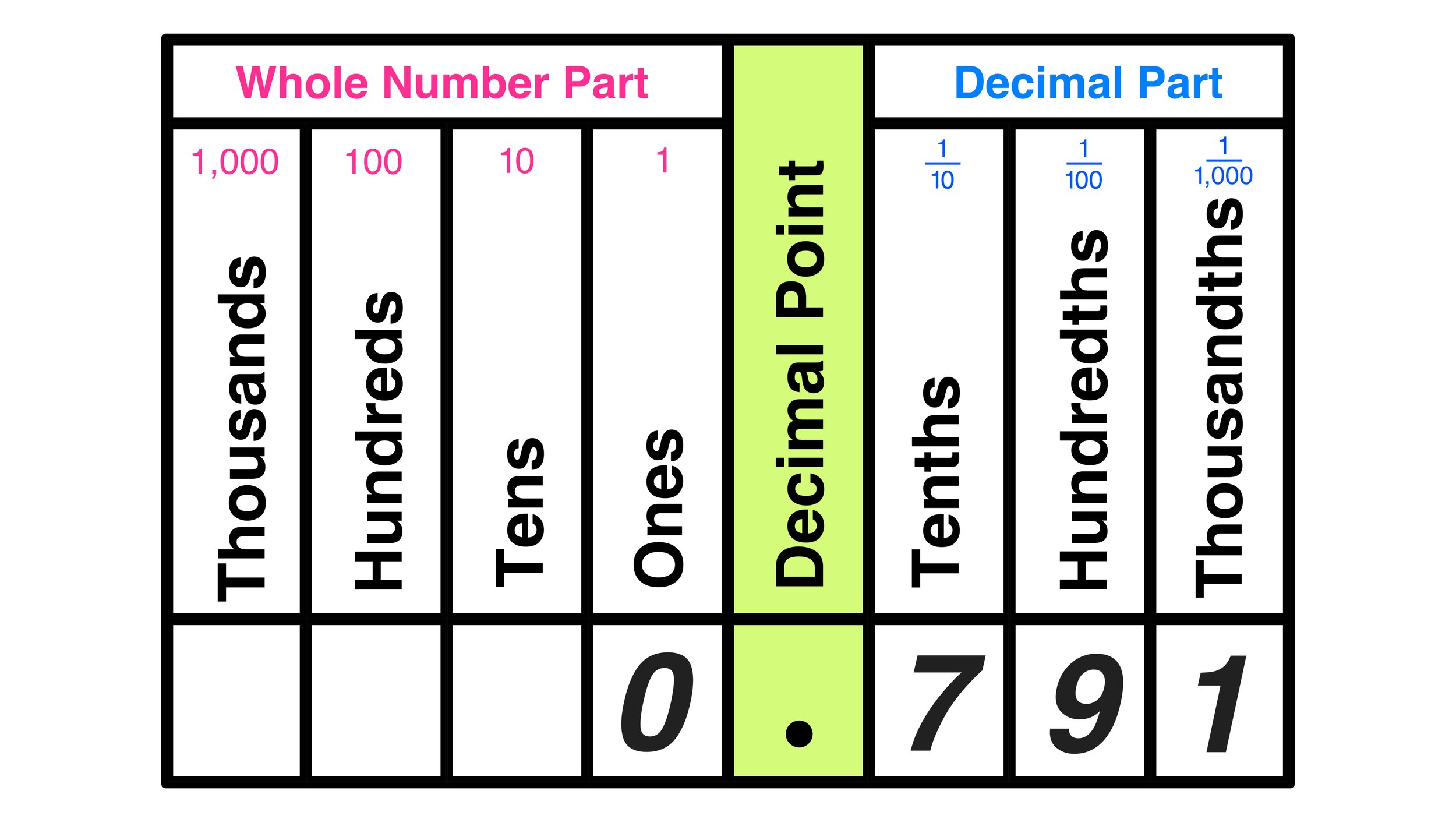
Example #2: Which digit is in the hundredths decimal place?

0.791

We can input this value into our chart as follows.

Using the chart, it is easy to see that the value in the hundredths place is 9.

0.791

Answer: 9

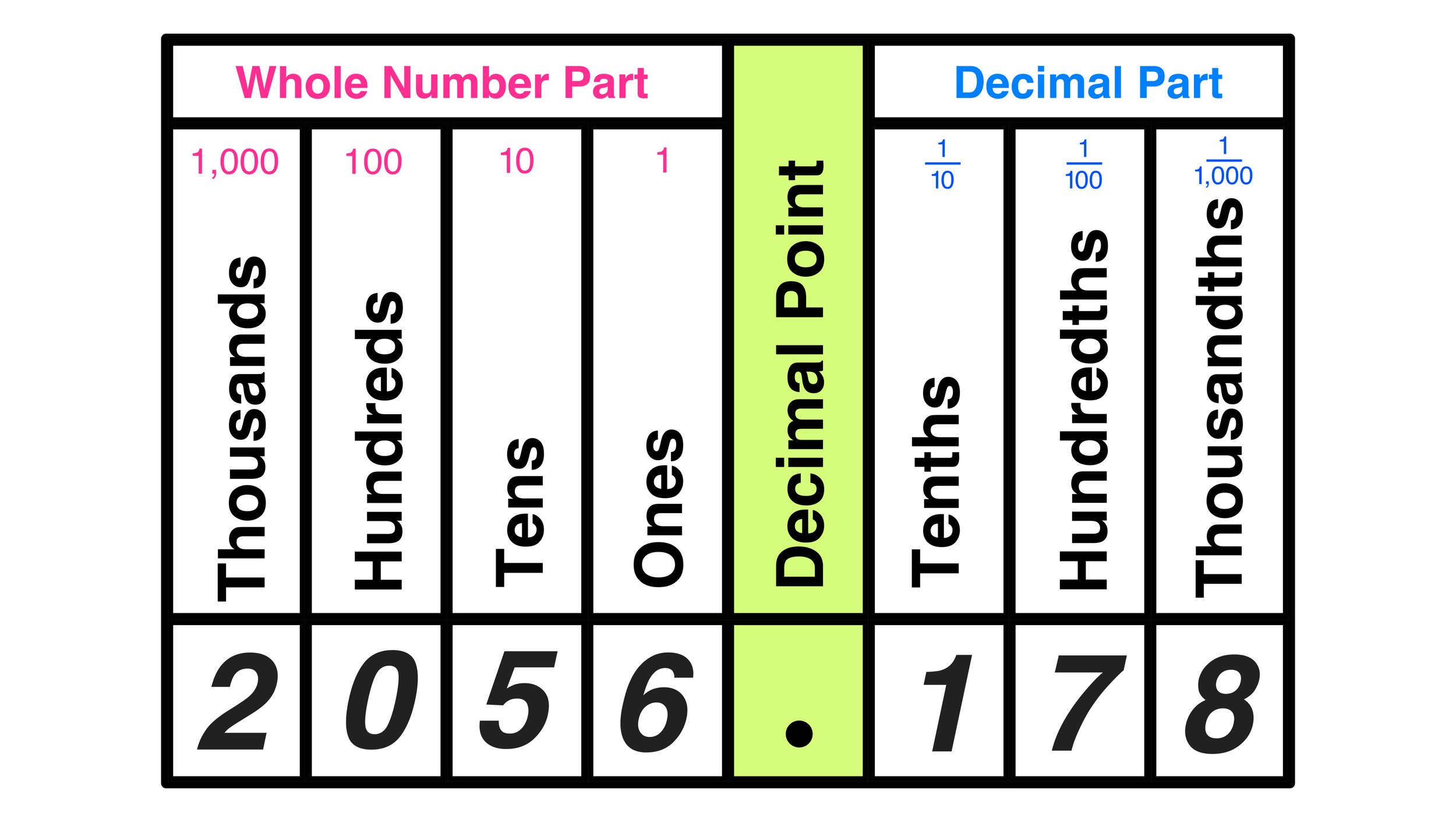
Example #3: Which digit is in the hundredths decimal place?

2,056.178

We can input this value into our chart as follows:

Using the chart, it is easy to see that the value in the hundredths place is 7.

2,056.178

Answer: 7

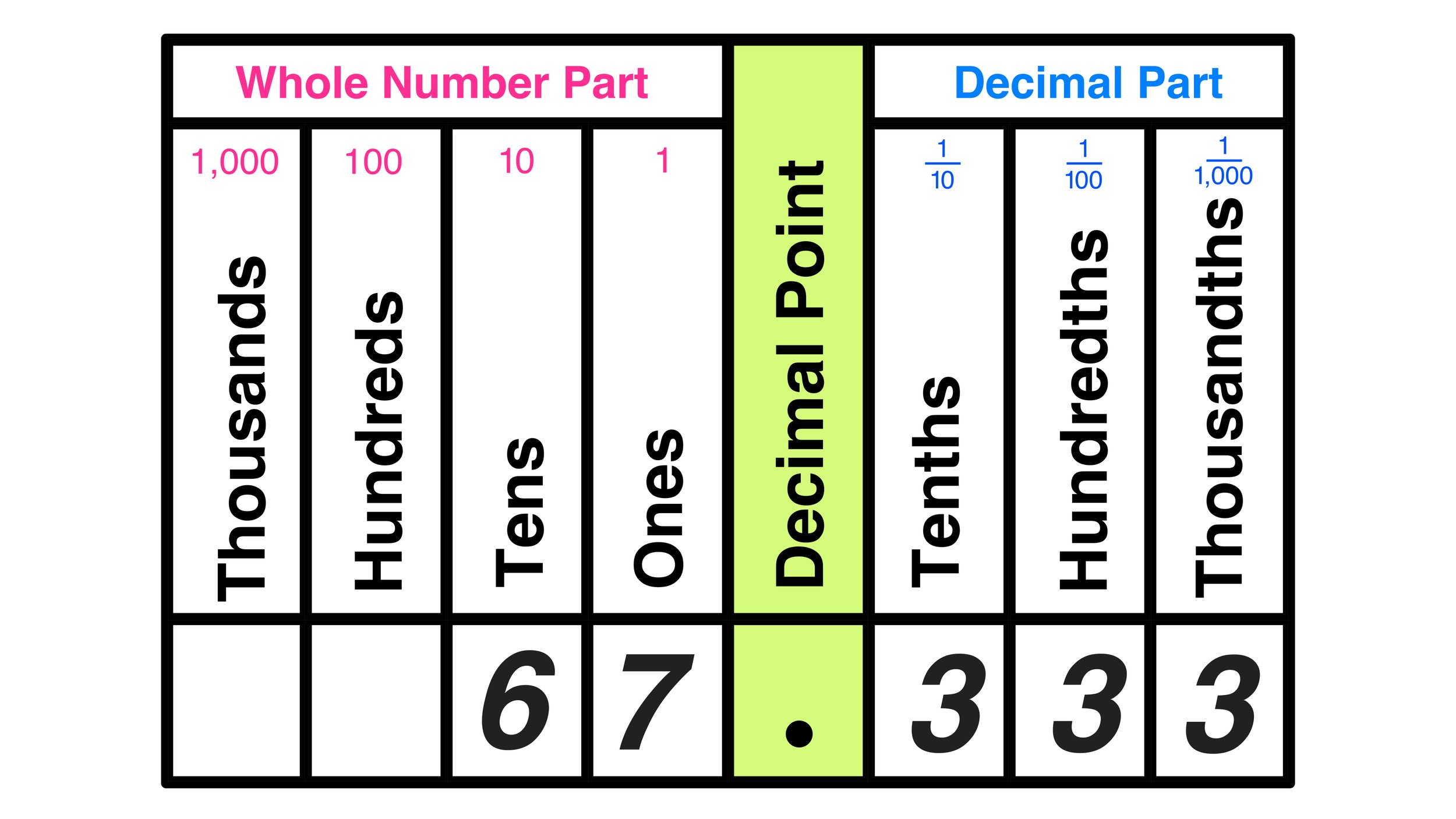
Example #4: Which digit is in the hundredths decimal place? 67.33333…

We can input this value into our chart as follows.

Using the chart, you can see that the hundredths place is 3.

Answer: 3

Example #5: Which digit is in the hundredths decimal place?

515.2

Notice that, at first glance, there is no value in the hundredths place.

However, 515.2 can also be expressed as 515.20

We can input this value into our chart as follows.

Using the chart, you can see that the hundredths place is 0.

Answer: 0

---

Extra Practice Problems

Which value is in the Hundredths Decimal Place?

By now, you should be more comfortable with identifying numbers occupying the hundredths decimal place.

Below, you will find 10 practice problems that will give you an opportunity to test your understanding of the hundredths place.

If you would like to use a chart to help you, click the link below to download a free blank place value chart!

▶ FREE DOWNLOAD: Decimal Place Value Chart (PDF File)

Practice Problems: Determine which number is in the hundredth place for each of the following:

 (Answer key to follow!)

1)   2.75

2)   56.333

3)   8.18

4)   403.212

5)   5,009.15

6)   0.04

7)   0.0004

8)   76.5333

9)   565.404

10)  10,214.133

---

Finished? Don’t scroll further until you are ready to see the answer key.

---

Answer Key

1)     2.75

2)     56.333

3)     8.18

4)     403.212

5)     5,009.15

6)     0.04

7)     0.0004

8)     76.5333

9)     565.404

10)10,214.133

Conclusion: Hundredths Decimal Place

In math, each digit position in any given number has its own unique place value “slot.” These positions or “slots” are referred to as place value.

While determining place value positions for integers can be relatively simple, the identification process becomes trickier when decimals values become involved.

Using a chart can be a helpful tool to help you to correctly identify place value for numbers that one, two, three, or more digits after a decimal point.

Namely, the hundredths decimal place refers to the second digit to the right of the decimal point.

---

Keep Learning: Free Math Guides

How to Solve Compound Inequalities (in 3 Easy Steps)

How to Solve Compound Inequalities in 3 Easy Steps

Being able to create, analyze, and solve a compound inequality using a compound inequality graph is an extremely important and helpful math skill that can be applied to many math concepts commonly found in pre-algebra, Algebra I, Algebra II, and even Pre-Calculus and Calculus. While many students may be intimidated by the concept of a compound inequality when they see unusual looking graphs containing circles and arrows, but working with compound inequalities is actually quite simple and straightforward.

 The following free How to Solve Compound Inequalities step-by-step lesson guide will teach you how to create, analyze, and understand compound inequalities using an easy and effective three-step method that can be applied to any math problem involving a compound inequality or a compound inequality graph. As a student, if you can follow the three steps described in this lesson guide, you will be able to easily and correctly solve math problems involving compound inequalities.

 Are you ready to get started? Before you learn about creating and reading compound inequalities, let’s review a few important vocabulary words and definitions related to inequalities.

What is an inequality?

Before we explore compound inequalities, we need to recap the exact definition of an inequality how they compare to equations.

What is an equation?

Definition: In math, an equation is a statement that shows that two mathematical expressions are equal to each other using an “=” sign.

For example, x=5 is an equation where the variable and x are equal to a value of 5 (and no other value).

It is important to note that equations are limited to only one possible solution, so, in this case, 5 is the only possible value that x can be equal to, and any other value would not apply.

 x=5

 The only solution: 5 

What is an inequality?

Definition: In math, an inequality is a relationship between two expressions or values makes a non-equal comparison.

For example, x>5 is an inequality that means “x is greater than 5,” where, unlike an equation that has only one solution, x can have infinitely many solutions, namely any value that is greater than 5.

We can visualize the simple inequality x>5 on the number line below as follows:

In comparison to equations, inequalities are not limited to only one possible solution. In fact, inequalities have infinitely many solutions.

 In this case, solutions to the inequality x>5 are any value that is greater than five (not including five).

 x>5

 Examples of solutions: 6, 7, 10, 105, 2,500 (all of these values satisfy the inequality because they are greater than 5)

 Examples of non-solutions: 5, 4, 0, -17, -1,001 (none of these values satisfy the inequality because they are not greater than 5)

What is the difference between an equation and an inequality?

Before we move onto exploring inequalities and compound inequalities, it’s important that you understand the key difference between an equation and an inequality.

 In essence, the key difference is between an equation and an inequality is:

• an equation has one and only one solution

• an inequality has multiple solutions

Graphing Inequalities on the number line

Now that you understand the difference between and equation and an inequality, you are ready to learn how solve compound inequalities and read compound inequality graphs.

But first, let’s quickly recap how to graph simple inequalities on the number line.

There are four types of inequality symbols:

• >: greater than

• <: less than

• ≥: greater than or equal to

• ≤: less than or equal to

It is important to understand the differences between these symbols, namely the significance of the line underneath a greater than or less than symbol and how it relates to the solution of an inequality and its graph on the number line.

For example, consider the following inequalities: x < 9 and x ≤ 9

The first inequality, x<9, has a solution of any value that is less than 9, but not including 9 (since 9 is not less than 9).

The second inequality x ≤ 9, has a solution of any value that is less than 9 AND the value 9 itself (since 9 is greater than or equal to 9).

On the number line, the difference between these two types of inequalities is denoted by using an open or closed (filled-in circle). The open circle means that the corresponding value is not included in the solution set, while the closed circle means that the corresponding value is included in the solution set.

Before moving forward, make sure that you fully understand the difference between the graphs of a < or > inequality and a ≥ or ≤ inequality. Understanding the difference in terms of the solution and the graph is crucial for being able to create compound inequality graphs and solving compound inequalities.

 For your reference, here are a few more examples of simple inequality graphs:

Again, an open circle means that the corresponding number line value is NOT included in the solution set. A filled-in circle means that it is included in the solution set.

---

What is a compound inequality? How to solve compound inequalities?

In the previous section of this guide, we reviewed how to graph simple inequalities on a number line and how these graphs represent the solution to one single inequality.

Definition: A compound inequality (sometimes referred to as a combined inequality) is two simple inequalities joined together.

Is it really that simple? Yes! A compound inequality is just two simple inequalities combined together and a compound inequality graph is just two simple inequalities graphed on the same number line.

There are two types of compound inequalities: or and and.

 Definition: An or compound inequality uses the word “or”  to combine two inequalities.

 Definition: An and compound inequality uses the word “and” to combine two inequalities.

To understand the difference between or and and inequalities, let take a look at a few examples apply the following 3-step process:

•  Step #1: Identify if the solving compound inequalities problem is or or and

•  Step #2: Graph both inequalities on the number line.

•  Step #3: Analyze  and determine the solution set.

---

How to Solve Compound Inequality Graphs Example #1: or

Example #1: Graph the compound inequality x<6  or  x>10

•  Step #1: Identify if the solving compound inequalities problem is or or and

 Step one is simple since every example will include the word or or and. In this first example, the word or is used, so make a note of that and move forward.

• Step #2: Graph both inequalities on the number line.

Next, graph both simple inequalities x<6 and x>10 on the number line to create the following compound inequality graph.

• Step #3: Analyze and determine the solution set.

Now that you have your graph, you can determine the solution set to the compound inequality and give examples of values that would work as solutions as well as examples of non-solutions.

For example, the values 4 and 14 are both solutions to this compound inequality, by the number 8 is not a solution.

Additionally, the values 6 and 10 are not solutions since they are included in the solution set since the circles are open.

The shaded area in the graph below represents the solution areas of the compound inequality graph.

---

How to Solve Compound Inequality Graphs Example #2: and

Example #2: Graph the compound inequality x>-2  and  x < 4

•  Step #1: Identify if the solving compound inequalities problem is or or and

Notice that this example uses the word and, so keep this in mind as it will affect how you analyze the solution to the compound inequality in step 3.

•  Step #2: Graph both inequalities on the number line.

Next, graph both simple inequalities x>-2 and x<4 on the number line to create the following compound inequality graph.

• Step #3: Analyze and determine the solution set.

This compound inequality has solutions for values that are both greater than -2 and less than 4.

So, for example:

• 0 is a solution because it satisfies both x>-2 and x<4.

• -4 is not a solution because it is only a solution for x<4 (a value must satisfy both inequalities in order to be a solution to this compound inequality)

• 8 is also not a solution since it does not satisfy both inequalities.

Note that this compound inequality can also be expressed as -2 < x < 4, which means that x is greater than -2 and less 4 (or that x is between -2 and positive 4).

---

How to Solve Compound Inequality Graphs: or vs. and

Based on the last two examples, did you notice the difference between or and and compound inequalities.

 Let’s compare the two graphs again:

The key difference here is that:

• The solution to or is examples are values that satisfy the first inequality or the second inequality. Notice that the compound inequality graphs never intersect (overlap).

• The solution to and examples are values that satisfy both the first inequality and the second inequality. Notice that the compound inequality graphs do indeed intersect (overlap).

Now, let’s take a look at three more examples that will more closely resemble the types of compound inequality problems you will see on tests and exams:

---

Solving Compound Inequalities Example #3:

 Solve for x: 2x+2 ≤ 14 or x-8 ≥  0

Don’t panic if this question looks tricky. You will still follow the exact same 3-step process used in examples 1 and 2, but you just have to do a little bit of algebra first.

In this case, before you use the three-step method, solve each inequality to isolate x as follows:

Now you are ready to apply the three-step method for x≤6 or x ≥ 8

• Step #1: Identify if the solving compound inequalities problem is or or and

You already know that this is an or compound inequality, so the graph will not have any overlap and any possible solutions only have to satisfy one of the two inequalities (not both).

• Step #2: Graph both inequalities on the number line.

Notice that greater than or equal to and less than or equal to symbols are used in this example, so your circles will be filled in as follows:

• Step #3: Analyze and determine the solution set.

Again, solving compound inequalities like this require you to determine the solution set, which we already figured out was x≤6 or x ≥ 8.

So, for example, here are a few examples of solutions and non-solutions:

•  10 is a solution because it satisfies one of the inequalities (x ≥ 8)

• 6 is a solution because it satisfied ones of the inequalities (x≤6)

• 7 is not a solution because it does not satisfy either inequality. This also applies to non-solutions such as 6.1 and 7.75.

---

Solving Compound Inequalities Example #4:

 Solve for x: 3x+1 ≥ 10 and 2x+7 >  7

 Just like the previous example, use your algebra skills to solve each inequality and isolate x as follows:

 Are you getting more comfortable with solving compound inequalities? Notice that the solution to this compound inequality is all values that satisfy x≥3 and x>0.

Now let’s go ahead and follow our three-step method:

• Step #1: Identify if the solving compound inequalities problem is or or and

Since this is an and compound inequality, we know that all solutions must satisfy both x≥3 and x>0

• Step #2: Graph both inequalities on the number line.

•  Step #3: Analyze and determine the solution set.

 Notice the intersection (or overlap area) of your compound inequality graph:

You can see that all of the solutions to this compound inequality will be in the region that satisfies x≥3 only, so you can simplify your final answer as:

 Solution: x≥3

 Additionally, here are a few examples of solutions and non-solutions:

•  5 is a solution because it satisfies both inequalities x x≥3 and x>0

• 3 is a solution because it satisfies both inequalities x x≥3 and x>0

• 2 is not a solution because it only satisfies one inequality

• 0 is not a solution because it only satisfies one inequality

• -1 is not a solution because it satisfies neither inequality

---

Solving Compound Inequalities Example #5:

 Solve for x: x+2 < 0 and 8x+1  ≥ -7

 Just as before, go ahead and solve each inequality as follows: 

After solving both inequalities, we are left with x<-2 and x≥-1

• Step #1: Identify if the solving compound inequalities problem is or or and

Note that his final example will demonstrate why step #1 is so important. Remember that solving this compound inequality requires you to find values that satisfy both x<-2 and x≥-1

•  Step #2: Graph both inequalities on the number line.

Again, this is an and problem, which means that you are looking for the intersection or overlap of the two lines on your compound inequality graph.

• Step #3: Analyze and determine the solution set.

Notice anything strange about this example? There is actually no area where the inequalities intersect!

Since we are looking for values that satisfy both inequalities,

We can conclude that there are no solutions because there is no value for x that is both less than -2 and greater than or equal to -1.

---

Conclusion: How to Solve Compound Inequalities Using Compound Inequality Graphs in 3 Easy Steps

You can solve any compound inequality problem by apply the following three-step method:

Step #1: Identify if the solving compound inequalities problem is or or and

•  Solutions to or compound inequality problems only have to satisfy one of the inequalities, not both.

• Solutions to and compound inequality problems must satisfy both of the inequalities.

• It is possible for compound inequalities to zero solutions.

 Step #2: Graph both inequalities on the number line.

 Step #3: Analyze and determine the solution set.

---

Keep Learning: Free Math Guides

Parent Functions and Parent Graphs Explained!

What are Parent Functions and Parent Function Graphs?

Learning about parent functions and parent graphs will give you better insight into the behaviors of a myriad of other functions that you will often come across in algebra and beyond. Your conceptual understanding of parent functions and their graphs is the key to working out transformations of equations and graphs.

The following free guide to Parent Functions and Their Graphs will explain what parent functions are, what their graphs look like, and why understanding their behavior is so important in math. In this post, we will explore the parent functions of the following commonly occurring functions:

• Absolute Value Parent Function

• Linear Parent Function

• Quadratic Parent Function

• Cubic Parent Function

• Exponential Parent Function

• Inverse Parent Function

• Square Root Parent Function

By the end of this guide, you will be able to identify the parent function of a function, use it to sketch graphs, and determine the function associated with a graph with ease!

Before you learn about parent functions and parent function graphs, let’s do a quick recap of some key vocabulary terms and definitions related to parent functions.

What is a parent function? What is a parent graph?

In math, a parent function is a function from a family of functions that is in its simplest form—meaning that it has not been transformed at all.

A parent graph is the graph of a parent function on the coordinate plane.

While these definitions may sound confusing at first glance, the concepts are actually pretty simple when you look at them visually.

For example, let’s consider the liner functions y=x and y=x+3.

In this case, the family of functions is the linear function (any function of the form y=mx+b) that represents a line of the coordinate plane.

So, in this case, y=x is the linear parent function, and y=x+3 is just a transformed version of the parent function (because it was shifted up three units from the original parent function’s position on the graph).

Again, notice that the function y=x is the linear parent function (the line y=x on the coordinate-plane is the parent graph) and that the function y=x+3 is a transformed version of the parent function (it was shifted 3 units upward).

All Parent Functions…

If you understand the linear parent function and what it represents, then you can understand all parent functions.

The animated GIF to the right further demonstrates what a linear parent function is and how it relates to all other linear functions.

The key takeaway right now is that every function family (linear, quadratic, cubic, square root, etc.) has a parent function which all other functions in that family can be derived from simply by transforming the basic parent function.

Parent Functions and Parent Graphs

What is a parent function and what are the parent function graphs?

Definition: A parent function is the most basic function from which a family of similar functions is derived. By performing various operations like addition, subtraction, multiplication, etc. on a parent function you obtain a function that belongs to the same family.

Parent function graphs are the graphs of the respective parent function. Any graph can be graphically represented by either translating, reflecting, enlarging, or applying a combination of these to its parent function graph.

Now, let’s find out in more detail about the parent functions and parent graphs of the following types of equations

1.     Linear

2.     Quadratic

3.     Cubic

4.     Exponential

5.     Inverse

6.     Square Root

7. Absolute Value

*Note that, in this guide, y= and f(x)= are used interchangeably and mean the same thing.

---

The Linear Parent Function

Linear Functions are one of the simplest types of functions you will learn. The general form of a single-variable linear function is f(x) = mx + b, where m, and b are constants, with a being non-zero.

Some examples of linear functions that are derived from the linear parent function are:

• f(x) = 2x +5

• f(x) = -3x +8

• f(x) = 5x + 10

The parent linear function is y = x, which is the simplest form from which members of the linear function’s family can be derived.

Linear Parent function : f(x) = x

The parent function graph of linear functions is a straight line with a slope of 1 and passes through the origin.

The graph of a function whose parent function is linear will always be a straight line. The features that uniquely identify each member in the family of linear functions are its slope and intercepts.

Examples of Linear Functions:

---

The Quadratic Parent Function

Quadratic functions are functions of the 2nd degree. The general form of a single-variable quadratic function is f(x) = a*x^2 + b*x + c, where a,b, and c are constants and a is non-zero.

Here are some examples of quadratic functions that are derived from the quadratic parent function:

• f(x) = x^2 - 6

• f(x) = x^2 + 3x

• f(x) = (-x+7)(x-2)

The quadratic parent function is f(x) = x^2

The parent function graph of quadratic functions is a parabola shape.

When we plot the graphs of the above-mentioned examples of quadratic functions, you can clearly see that they too have derived the characteristic parabola shape from their quadratic parent function.

Examples of Quadratic Functions:

---

The Cubic Parent Function

Cubic functions are third-degree functions. The general form of a single-variable cubic function is f(x) = a*x^3 + b*x^2 + c*x +d, where a,b,c, and d are arbitrary constants and a is non-zero.

A few examples of cubic functions that are derived from the cubic parent function include:

• f(x) = x^3 + 4

• f(x) = -x^3 + 3

• f(x) = 2x^3 - 3x^2 - 6x

 The cubic parent function is f(x) = x^3

If we take the third cubic function example, y = 2x^3 - 3x^2 - 6x, it will seem that the function is drastically different from the parent function yet visually the parent function graph, and the graph of the cubic function below aren’t far apart (see the graphs below for reference)

Examples of Cubic Functions:

As with visual similarity, functions also show behavioral similarity with their parent functions, which is why it is important to learn about them.

---

The Exponential Parent Function

Exponential functions are quite often used to mathematically represent the growth and decay of populations, investments, etc. The parent exponential function is f(x) = b^x, where b, commonly referred to as the base, is a positive non-zero number.

Examples of exponential functions that are derived from the exponential parent function include:

• f(x) = 1.5^x

• f(x) = e^(x - 10)

• f(x) = 0.4^x + 10

You can look for variables present in the exponents of a function to easily identify if a function’s parent function is exponential.

The parent exponential graph f(x) = e^x is shown below:

Note that in the parent exponential graph the graph tends towards y = 0 as x goes towards negative infinity. This is the horizontal asymptote of the function. You will come across horizontal asymptotes for functions whose parent function is exponential.

 Next, let’s see how the example exponential functions graphs look. See if you can determine their horizontal asymptotes.

Examples of Exponential Functions:

---

The Inverse Parent Function

Inverse functions also known as reciprocal functions have the variable (x) at the denominator of the function.

The parent inverse function is f(x) = 1/x.

Some examples of functions that fall under the family of inverse functions that are derived from the inverse parent function include:

• f(x) = 3/x

• f(x) = 1/(x+10)

• f(x) = 2/(2x+3)

The parent inverse function has a vertical asymptote at the y-axis (x = 0), which can be seen in the behavior of the graph as x tends to 0.

Hence the presence of vertical asymptotes in a graph may be an indication that the parent function is inverse. Do you recognize the vertical asymptotes in the graphs of the example inverse functions below?

Examples of Inverse Functions:

---

The Square Root Parent Function

The parent function of square root functions is f(x) = sqrt(x).

The following are examples of square root functions that are derived from the square root parent function:

• f(x) = sqrt(x+1)

• f(x) = sqrt(3x -9)

• f(x) = sqrt(-x)

The parent square root function has a range above 0 and a domain (possible values of x) of all positive real values. Therefore, the parent graph f(x) = sqrt(x) looks as shown below:

The graphs of the square root function examples also have their domains restricted.

Examples of Square Root Functions:

*Note: From the types of parent functions discussed in this blog, only functions derived from the square root and inverse parent functions inherit domain restrictions. You can use this pattern to distinctly identify functions from others.

---

The Absolute Value Parent Function

The final parent function covered in this guide is the absolute value parent function f(x) = | x |.

The following are examples of absolute value functions derived from the absolute value parent function:

• f(x) = | x+4 |

• f(x) = | 3x | - 4

• f(x) = - | x - 1 | + 8

The absolute value parent function is defined by its V-shape with a sharp and pointy vertex. Take a close look at the absolute value function examples below to see their relationship to the parent function.

Examples of Absolute Value Functions:

---

Conclusion: Parent Functions and Parent Graphs

There are infinitely many functions, yet all functions can be classified as a derivation of a particular parent function. Functions tend to inherit behaviors and characteristics such as domain restrictions, range, asymptotes, etc. from their respective parent function. Hence, understanding the patterns of parent functions and their graphs will make it easier for us to handle complicated functions.

Need More Help?

Check out our animated video lesson on the parent functions and their transformations:

Keep Learning:

The Vertical Line Test Explained in 3 Easy Steps

What is the Vertical Line Test in Math?

Key Question: What is the vertical line test function and how can it be used?

Learning how to identify whether or not a given relation is a function is an extremely important math skill (most notably in pre-algebra and algebra). Luckily, there is a simple and handy tool called the vertical line test that you can always use to see if a relation can be considered a function or not just by looking at its graph.

This free Vertical Line Test step-by-step guide will teach you how to figure out whether or not a relation is or is not a function by looking at its graph and using a simple mathematical tool called the vertical line test.

Before you learn how to use the vertical line test, we will do a quick review of some very important vocabulary and definitions related to functions and relations.

Are you ready to get started?

Vertical Line Test Definitions and Vocabulary

What is a relation?

Definition: A relation is how a set of inputs and outputs of a system are related to each other. Mappings and graphs are the most common ways of representing relations. The figures below show a graphic and map representation of the relation between a set of numbers and the square of those numbers.

Figure 01: Relation Mapping

Figure 02: The graph representing the relation in Figure 01.

What is a function?

Definition: A function is a relation between a set of inputs and outputs where, for every input, there is one (and only one) output. In other words, a function is a relation where every input has only one output.

If this is confusing, observe the mappings in Figure 03 and Figure 04 below for more insight.

Figure 03: The relation is a function.

Figure 04: The relation is NOT a function.

The relation mapping in Figure 03 represents a function because every input (or x-value) has only one unique output (or y-value).

The relation mapping in Figure 04 does not represent function because at least one of the inputs (in this case 6) has more than one output. If you look at the mapping, you will notice that 6 has two outputs: 1 and 3. Thus, the relation in Figure 04, by definition, is not function.

Keep this information in mind as we move on and extend your understanding of relations and functions to looking at graphs and learning how to apply the vertical line test.

What is the difference between a relation and a function?

Functions are a subset of relations. Simply put, all functions are relations, but not all relations are functions.

In other words, a relation represents the relationship between an input and an output, while a function—more specifically—is a type of relation where there is only one output for each input.

What is the Vertical Line Test Function?

Now that you understand how to determine whether or not a relation is a function by looking at a mapping, you are ready to learn to make this same determination just by looking at a relation’s graph and using a tool called the vertical line test.

The Vertical Line Test helps you to determine if a given relation is a function. Now, let's find out how the vertical line test works with realistic examples.

Again, for a relation to be a function, the relation must have exactly one output for a given input. Let's revisit the relations shown in Figure 03 and Figure 04, but this time we will represent them graphically:

Figure 05: The graph of the relation in Figure 03, which was, by definition, a function.

Figure 06: The graph of the relation in Figure 04, which was, by definition, not a function.

We already know that the graph in Figure 05 represents a function and that the graph in Figure 06 does not represent a function because we already applied the definition of a function to the corresponding mappings.

But what if we had to make this determination using only the graph without the mappings? This is where the vertical line test comes into play.

The Vertical Line Test Explained in 3 Easy Steps

The vertical line test is a simple and straightforward tool for determining whether not the graph of a relation represents a function or not.

Applying the vertical line test is as easy as following these 3 easy steps:

Step One: Observe the given graph and draw one or multiple vertical lines through the graph.

Step Two: Note how many times the vertical line(s) that you drew intersected the graph (either coordinate points or a line/curve).

Step Three: Based on the number of intersections, determine whether or not the relation is a function.

• If your vertical line intersects the graph only once, then the relation is a function.

• If your vertical line intersects the graph more than once at any point, the relation is not a function.

We can apply the vertical line test to the graphs from Figure 05 and Figure 06 below to confirm what we already knew (that one graph represents a function and the other does not).

Figure 07: The vertical line test confirms that the relation is a function because there is only one intersection point.

Figure 08: The vertical line test confirms that the relation is a not function because there are multiple intersection points.

Notice how the vertical line drawn on the graph in Figure 07 only has one intersection point. Furthermore, there are no other areas on the graph where you could draw a vertical line where there would be more than one intersection point. Therefore, the graph represents a function.

Notice how the vertical line drawn on the graph in Figure 08 has multiple intersection points (namely through (6,1) and (6,3)), therefore this graph does not represent a function.

Now that you understand how the vertical line test works, let’s apply it to three more examples…

Vertical Line Test Examples

Directions: Use the vertical line test to determine whether or not the graph of each relation is a function.

Example A: Is the relation a function?

We can determine whether or not this graph represents a function by drawing one (or multiple vertical lines) through the graph to see if there is any point where the line intersects the graph more than once (if it does, then the relation is not a function).

The vertical line test shows…

Here we can clearly see that the relation fails the vertical line test and that the graph does not represent a function because there are multiple intersection points.

Final Answer: The relation is not a function because it fails the vertical line test.

Example B: Is the relation a function?

Again, you can use the vertical line test to determine whether or not the graph above represents a function.

Here we can clearly see that the relation passes the vertical line test and that the graph represents a function because there is only one intersection point.

Final Answer: The relation is a function because it passes the vertical line test.

Example C: Is the relation a function?

Are you starting to get the hang of it? Go ahead and apply the vertical line test to see if the graph of the circle represents a function.

Here we can clearly see that the relation fails the vertical line test and that the graph does not represent a function.

Final Answer: The relation is not a function because it fails the vertical line test.

(This will always be the case with circles)

Example D: Is the relation a function?

Remember that the graph of a relation has to pass the vertical line test everywhere in order to confirm that the relation is a function.

For example, if you drew your vertical line at x=-10 as in Figure 09 below, you might incorrectly conclude that the graph passes the vertical line test (since there is only one intersection point).

But, if you draw multiple vertical lines, such as the one through x=2 in Figure 10 below, you will see that this graph actually fails the vertical line test.

Figure 09: Does the vertical line test pass everywhere?

Figure 10: If the vertical line test fails anywhere on the graph, then the relation is not a function.

Final Answer: The relation is not a function because it fails the vertical line test.

Conclusion/Recap:

The vertical line test is a simple, yet effective tool that can be used to determine whether or not the graph of any given relation represents a function (a specific type of relation where for every input there is one and only one output). To make this determination, simply draw a vertical line through the graph and see how many times the vertical line intersects with the graph of the function. If the vertical line only intersects with the graph one time at any given point, then the graph represents a function. However, if the vertical line intersects with the graph at any point more than once, then the graph does not represent a function.

Recap:

Search Tags: vertical line test, vertical line test function, vertical line test examples, the vertical line test, vertical line test definition math, vertical line test to determine function, vertical line test practice

Keep Learning:

10 Free Counting Worksheets for Kindergarten

10 Free Counting Worksheets for Kindergarten

A Post By: Anthony Persico

Are Your Kindergarten Students Ready for These Fun and Engaging Counting Worksheets (with answer keys)?

One of the most fundamental and important math skills is basic counting. This key skill is first introduced at the pre-school and kindergarten levels and forms as the foundation of all math topics that follow (counting beyond single digits, grouping, addition, subtraction, working with money, etc.).

While there are tons of free kindergarten math worksheets available online, they are not all created the same. Many free worksheets are simply bland and uninteresting, leaving much to be desired and often leading children to start their mathematics journey off on the wrong foot. After all, we never want our students to see mathematics as a dull or boring subject (when it is, in fact, quite the opposite).

However, if you are looking for free counting worksheets for kindergarten students that are actually fun and engaging, then you’re in the right place. In today’s post, you will find 10 Free Counting Worksheets that can be download as pdf files, which are easy to print or share digitally.

These colorful worksheets give students an opportunity to practice and apply their counting skills in the context of “find the fib” or “two truths and one lie,” where students are given three counting examples or diagrams (two of which are true and one of which is false) and must figure out which choice is a fib. Why are these kinds of worksheets so effective for helping students to improve their counting skills? Because they require students to think deeply and actually apply their concepts of numbers and counting in a way that allows them to think critically and mathematically (and have fun at the same time).

Ready to see the results for yourself? Go ahead and download and share a few of our free counting worksheets with your kindergartners and see how they react. If you find the worksheets useful and would like to gain access to all of our kindergarten math activity libraries, you can click here to learn more about our membership program and sign up for a 7-day free trial.

Are you ready to download your Free Counting Worksheets for Kindergarten Students?

• Use the links below to download and save each worksheet as a pdf file.

• Each worksheet includes a sample image so you can preview the worksheet before downloading.

• The second page of each worksheet includes an answer key.

• While working on these worksheets, we recommend that you encourage your students to explain why they chose a statement as being untrue. You can take it a step further by asking them how they should change the statement to make it true.

• Whenever you find an answer, ask the question “does this solution make sense?”

---

10 Free Counting Worksheets for Kindergarten

How to Download and Print:

Below you will find preview images and links to download all ten kindergarten math worksheets. There will also be a link denoted by a download symbol ⤓. Once you click on one of these links, the corresponding worksheet will download in a new window as a PDF file. Once the file is downloaded, you can save it to your personal device and or print the worksheet.

If you need a more detailed explanation of how to save and/or print any of these free pdf worksheets, please view our video tutorial by clicking this link.

*Note that you can click on any of the worksheet images to see an enlarged preview before you download.

---

Counting Worksheet #1:

Topic: Counting Numbers 1-5

Worksheet Download:

⤓ Click here to download your pdf worksheet

Answer: Choice B is a fib!

Suggested:

10 Free Kindergarten Math Worksheets for Ages 4+

View fullsize

---

Counting Worksheet #2:

Topic: Counting Numbers 6-10

Worksheet Download:

⤓ Click here to download your pdf worksheet

Answer: Choice B is a fib!

Suggested:

Do you want Free K-12 Math Resources, Lesson Plans, and Activities in your inbox every week?

View fullsize

---

Counting Worksheet #3:

Topic: Counting Numbers 1-10, Grouping

Worksheet Download:

⤓ Click here to download your pdf worksheet

Answer: Choice A is a fib!

Suggested:

11 Super Cute Math Jokes and Puns for Kids

View fullsize

---

Counting Worksheet #4:

Topic: Grouping, Identify More Than or Less Than

Worksheet Download:

⤓ Click here to download your pdf worksheet

Answer: Choice A is a fib!

Suggested:

Why You Should Be Using "Which One Doesn't Belong?" to Ignite Student Thinking in Math

View fullsize

---

Counting Worksheet #5:

Topic: Grouping, Identify More Than or Less Than

Worksheet Download:

⤓ Click here to download your pdf worksheet

Answer: Choice C is a fib!

Suggested:

Number Bonds Explained! (Free Worksheet Included)

View fullsize

---

Counting Worksheet #6:

Topic: Grouping, Counting Numbers 1-10

Worksheet Download:

⤓ Click here to download your pdf worksheet

Answer: Choice C is a fib!

Suggested:

Play with Math! 10 Fun Ideas for All Ages

View fullsize

---

Are you looking for more super fun Kindergarten Math Worksheets?

The best-selling workbook 101 Kindergarten Math Worksheets: Super Fun Math Activities for Ages 4-7 is now available as a PDF download. You can get yours today by clicking here.

---

Counting Worksheet #7:

Topic: Grouping, Counting Numbers 1-10

Worksheet Download:

⤓ Click here to download your pdf worksheet

Answer: Choice C is a fib!

Suggested:

Free Printable Fraction Chart for Kids

View fullsize

---

Counting Worksheet #8:

Topic: Grouping, Counting Numbers 10-15

Worksheet Download:

⤓ Click here to download your pdf worksheet

Answer: Choice B is a fib!

Suggested:

Bar Charts and Bar Graphs Explained!

---

Counting Worksheet #9:

Topic: Grouping, More/Less Than, Counting up to 20

Worksheet Download:

⤓ Click here to download your pdf worksheet

Answer: Choice A is a fib!

Suggested:

Free Printable Multiplication Chart (Times Table Practice for Kids)

View fullsize

---

Counting Worksheet #10:

Topic: Grouping, Comparing Numbers, Counting up to 20

Worksheet Download:

⤓ Click here to download your pdf worksheet

Answer: Choice B is a fib!

Suggested:

101 Kindergarten Math Worksheets Workbook for Ages 4-7

View fullsize

---

Thoughts? Share your questions and suggestions in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math and an advisor to Amazon Education's 'With Math I Can' Campaign. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

You Might Also Like…