Free Printable Math Puzzles for Middle School Students

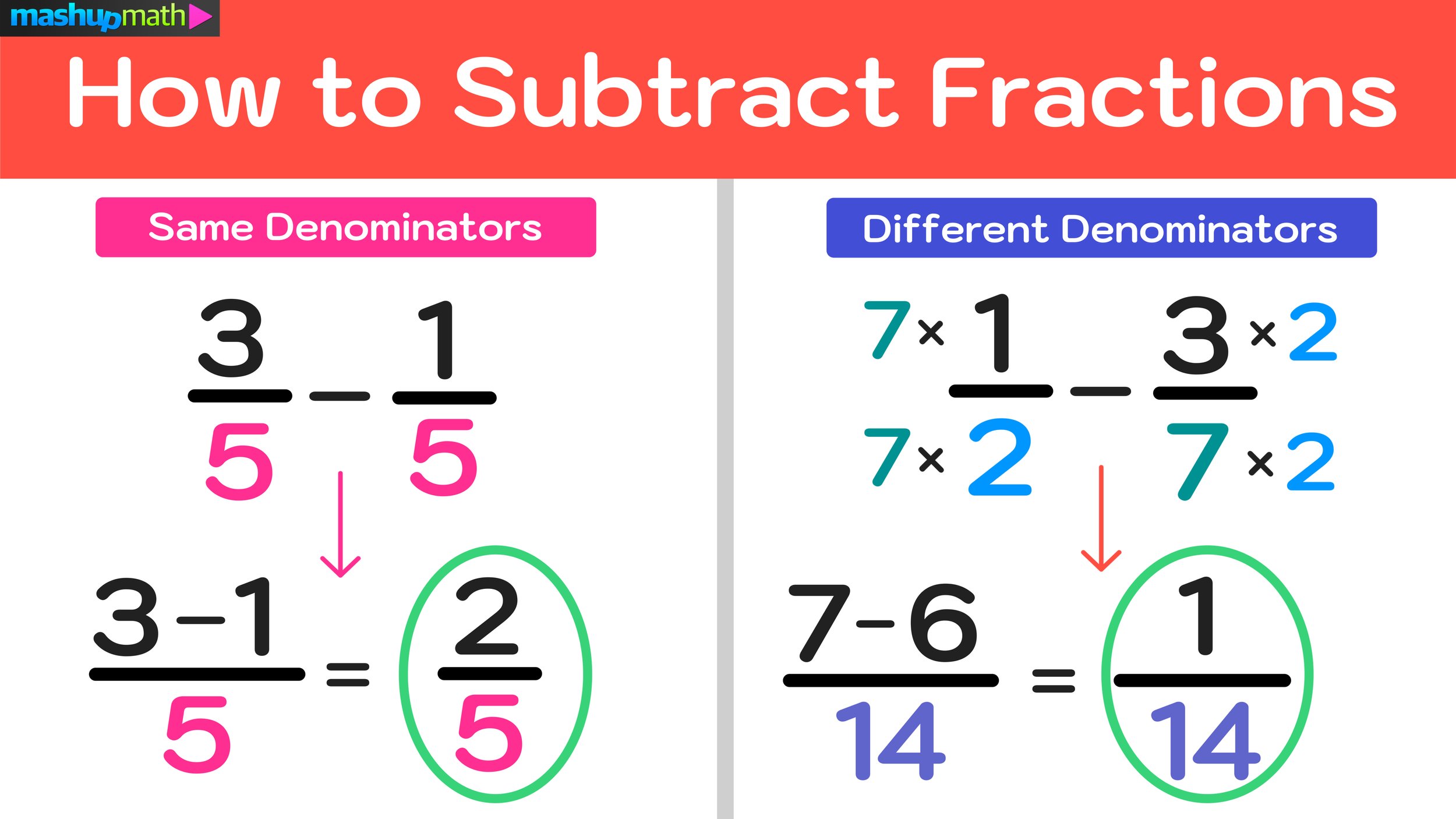
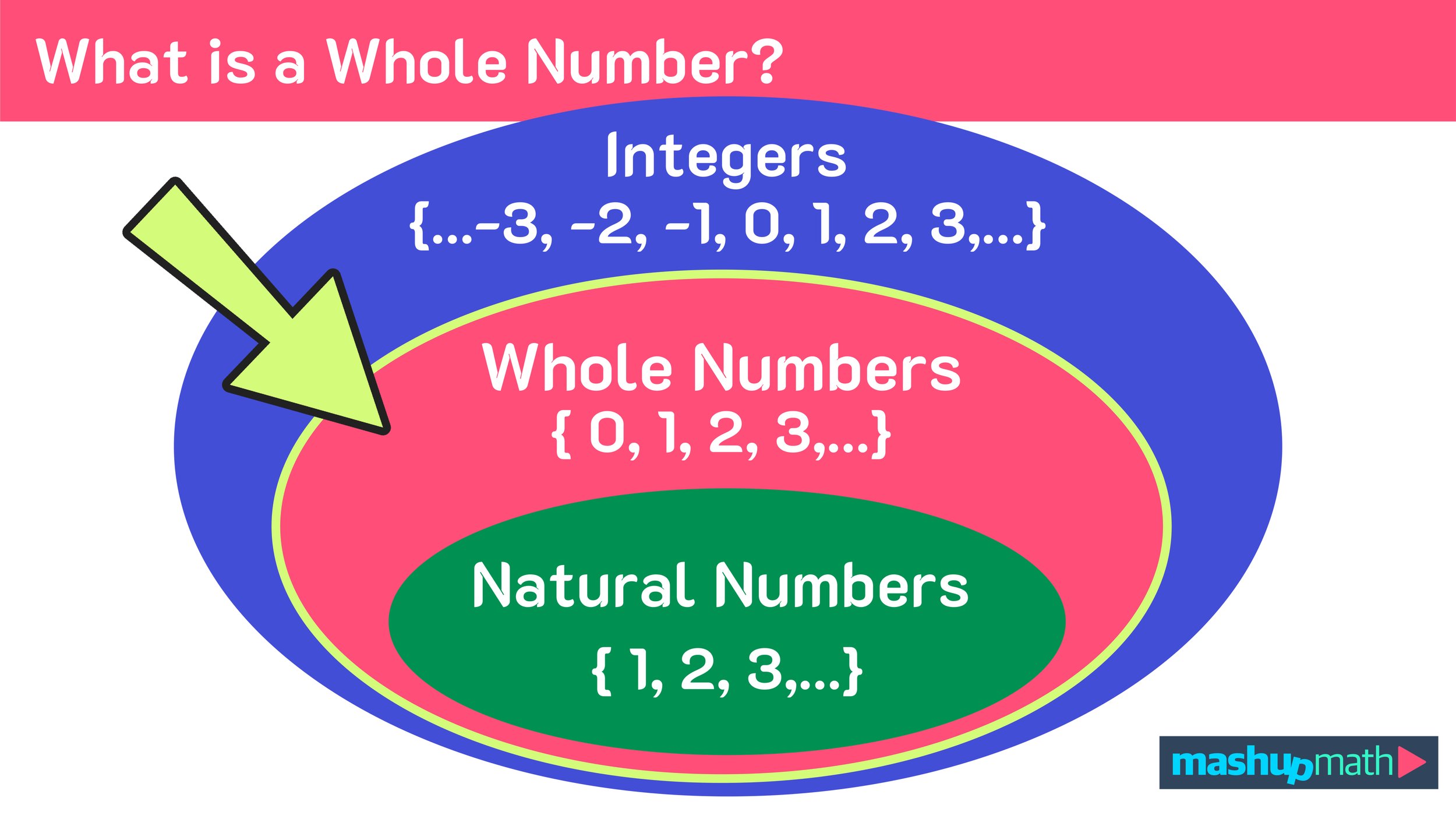
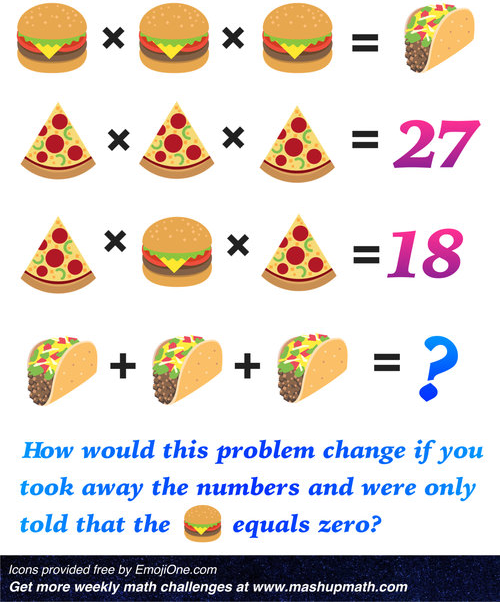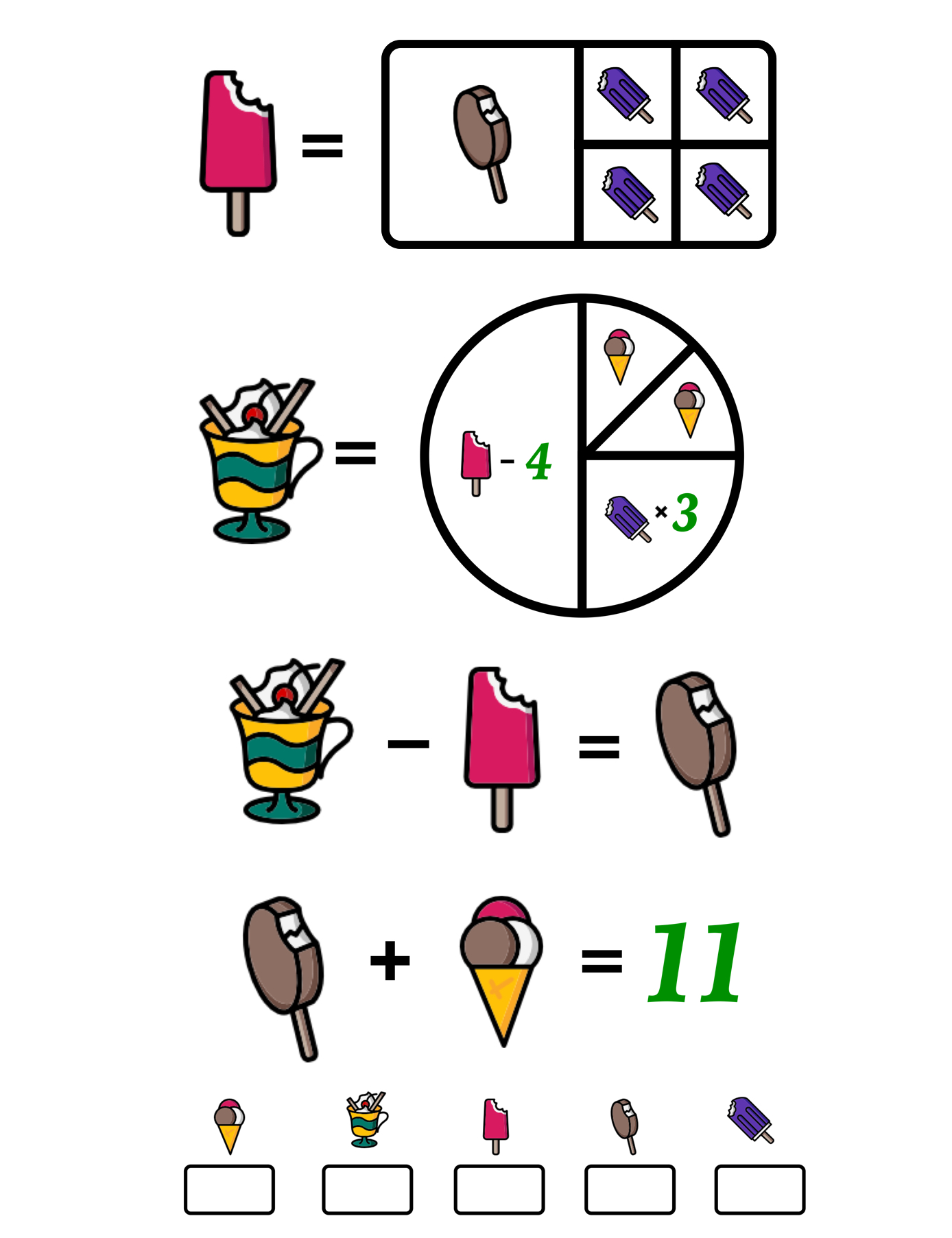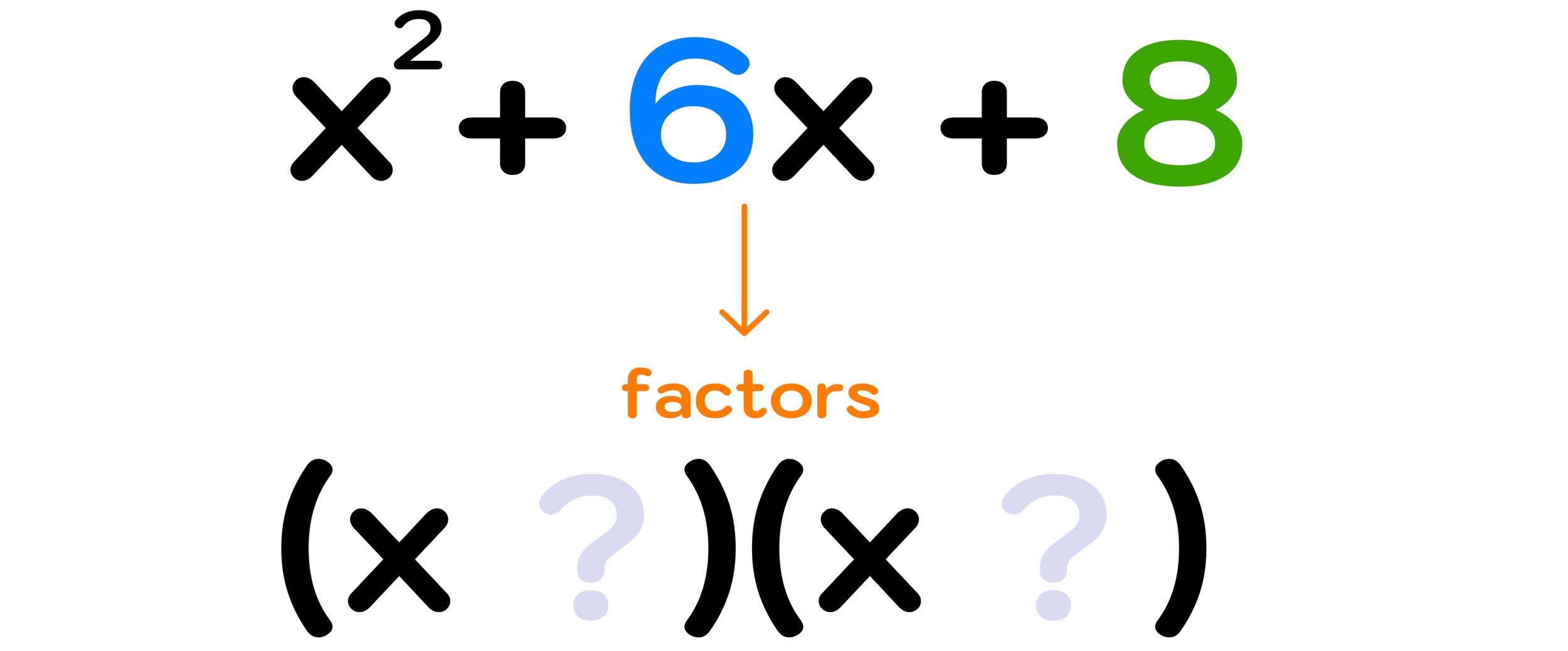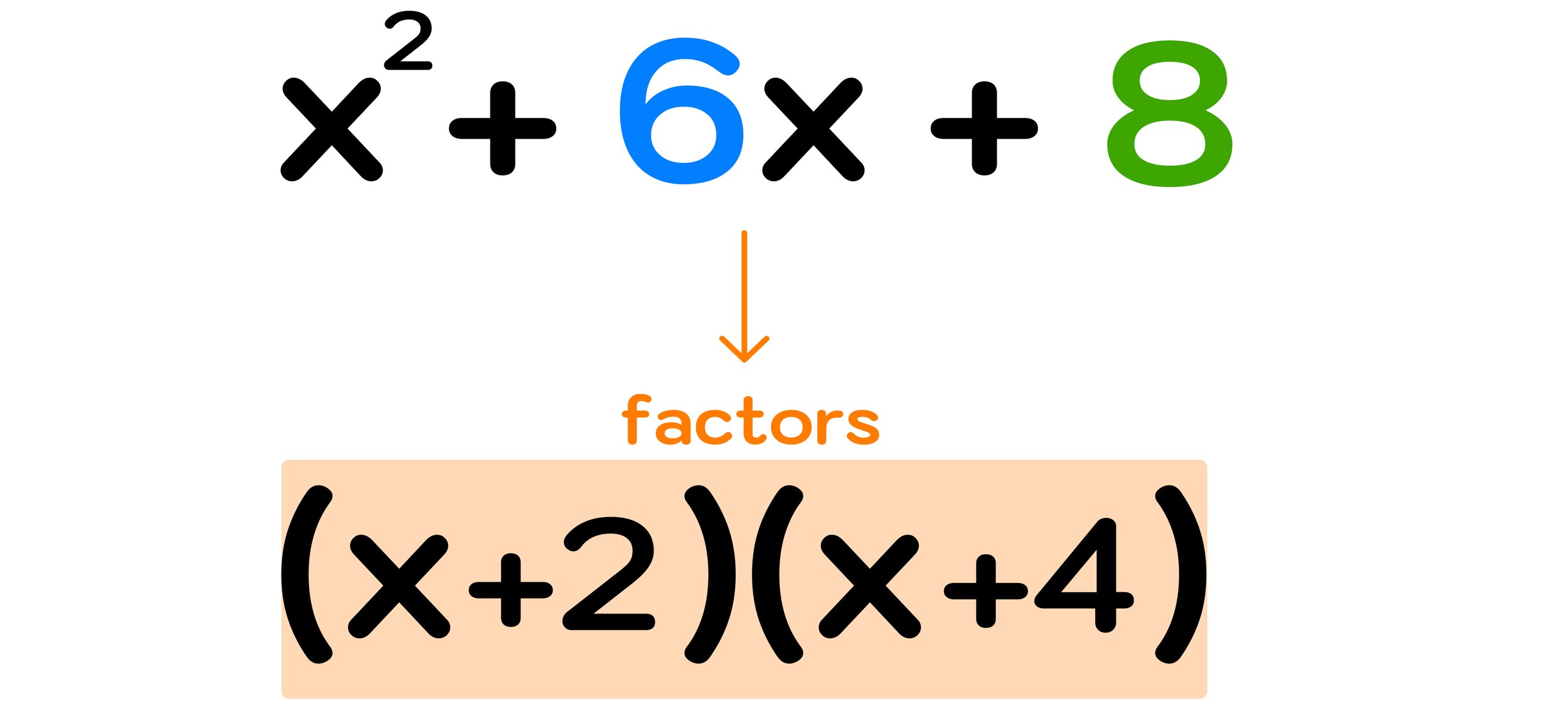Are you looking for some fun, printable math puzzles for middle school students?

These 5 math puzzles will engage your students and get them thinking creatively and visually about math topics including fractions, areas models, the order of operations, and even algebra!

So, can your middle schoolers solve these fun middle school math puzzles? Let’s get started and find out!

---

Math Puzzles for Middle School Students #1

This first math puzzle for middle school challenges students to use their knowledge of the order of operations to find the value of each symbol (the hamburger, the taco, and the pizza) and the ‘?’ in the puzzle below.

Solution: Pizza = 3, Hamburger = 2, Taco = 8

---

Math Puzzles for Middle School Students #2

The second math puzzle is a Multiplication Table activity where students have to use their knowledge of multiplication and multiplication facts to find the value of each symbol in the grid below.

Solution: Volcano = 1, Statue of Liberty = 3, Rocket = 6, Race Car = 2, Ferris Wheel = 18

---

Math Puzzles for Middle School Students #3

Our third math puzzle for middle school students is a math logic puzzle that challenges students to use their number sense to recognize numerical patterns to solve the puzzle.

Solution: Multiple solutions exist using each value only once.

---

Math Puzzles for Middle School Students #4

The next middle school math puzzle is an area model problem where students have to find the value of each symbol to complete the area model and determine which two numbers are being multiplied together.

Solution: Pretzel = 8, Mustard = 3, Chocolate-Covered = 50, Salt = 40, Sticks = 24

---

Math Puzzles for Middle School Students #5

The final math puzzle for middle school students is a fraction model puzzle where students are tasked with using their knowledge of fractions to find the value of each symbol.

Solution: Pink = 16, Chocolate = 8, Purple = 2, Ice Cream Cup = 24, Ice Cream Cone = 3

---

Are you looking for more daily math challenges and puzzles to share with your kids?

My best-selling workbook 101 Math Challenges for Engaging Your Students in Grades 3-8 is now available as a PDF download. You can get yours today by clicking here.

---

Read More Posts About What’s Trending in Math Education:

How to Factor Quadratic Equations—Step-by-Step Examples and Tutorial

How to Factor Quadratic Equations Explained

Step-by-Step Guide: How to Factor a Quadratic Equation, How to Solve Quadratic Equations by Factoring

Step-by-Step Guide: How to factor a quadratic equation explained.

In algebra, a quadratic equation is an equation of the form ax² + bx + c = 0 where a can not equal zero.

The word quad is Latin for four or fourth, which is why a quadratic equation has four terms (ax², bx, c, and 0). Being able to solve quadratic equations by factoring is an incredibly important algebra skill that every student will need to learn in order to be successful in Algebra I, Algebra II, and beyond. Learning how to factor a quadratic equation comes down to being able to recognize a quadratic equation, being able to factor it, and then finally being able to solve for x and check your answer for mistakes.

This free Step-by-Step Guide on How to Factor Quadratic Equations will cover the following topics:

• What is a Quadratic Equation?

• What are the Solutions of a Quadratic Equation?

• How to Factor Quadratic Equations when a=1

• How to Factor Quadratic Equations when a≠1?

Note that this guide is a follow-up to our free step-by-step guide How to How to Factor Polynomials, which reviews how to factor polynomials with 2 terms, 3 terms, and 4 terms. While we will review general factoring in this guide, we will be more focused on how to factor a quadratic equation.

However, before we learn how to factor quadratic equations and how to solve quadratic equations by factoring, let’s quickly review some important vocabulary terms related to quadratics and quadratic equations.

Figure 01: What is the difference between a trinomial expression and a quadratic equation.

What is a Trinomial Expression?

While the focus of this guide is on teaching you how to factor quadratic equations and how to solve quadratic equations by factoring, it is important that you first understand how the difference between a trinomial expression and a quadratic equation.

In algebra, a trinomial expression is a polynomial with 3 terms of the form ax² + bx + c. Note that, since it is an expression, a trinomial does not include an equal sign.

• ax² + bx + c

What is a Quadratic Equation?

In algebra, a quadratic equation is a trinomial of the form ax² + bx + c that is equal to zero. So, we can say that a quadratic equation is of the form:

• ax² + bx + c = 0

Figure 01 above illustrates this key difference between trinomial expressions and quadratic equations, which is namely that a quadratic equation is an equation and includes a fourth term (=0).

Why are we concerned with quadratic equations being equal to zero? You may already know that, when graphed, quadratic equations can be represented on the coordinate plane as a parabola (a U-shaped curved). When we solve quadratic equations by factoring, we are actually figuring out where the parabola crosses zero on the x-axis, as shown in Figure 02 below.

Figure 02: By setting a quadratic equation equal to zero, we are able to determine where the parabola crosses the x-axis. These x-values will be the solution(s) to a quadratic equation. This guide will teach you how to solve quadratic equations by factoring (not graphing).

Consider the example quadratic in Figure 02 above:

• x² +6x + 8 = 0

Notice that, for this quadratic equation, a=1, b=6, and c=8. When it comes time to learn how to factor a quadratic equation later on, it will be important that you are able to identify the values of a, b, and c for any given quadratic equation.

Now, here are two key pieces of information about the solutions to quadratic equations:

• The solution(s) to any quadratic equation are the points where the graph of the quadratic crosses the x-axis on a graph.

• Quadratic equations typically have two solutions, but they can also have one solution or zero solutions.

• You do not have to graph quadratic functions to solve them. You can solve quadratic equations by factoring.

Now that you understand what the solutions of a quadratic represent graphically, you are ready to learn how to factor equations and solve them algebraically.

Are you ready to get started?

---

How to Factor Quadratic Equations: Intro

Let’s start by factoring the example quadratic equation from Figure 02 above: x² +6x + 8 = 0

Example #1: Factor and Solve x² +6x + 8 = 0

From our graph, we already know that this quadratic equation will have two solutions: x=-4 and x=-2 (note that this can also be written as x={-4,-2}). So, let’s use factoring to find these answers algebraically.

To factor a quadratic equation, we can split it up into two parts:

• The left side of the equal sign

• The right side of the equal sign

On the left side of the equal sign, we must have a trinomial of the form ax² + bx + c to deal with and, on the right side, we must have a zero. If the quadratic equation in question is not in this form, we will have to use algebra to rearrange it. However, this first example is good to go so we don’t have to move any of the terms around. This first step is shown in Figure 03 below:

Figure 03: How to factor a quadratic equation.

From here, the next step is to factor the trinomial on the left side of the equal sign:

• x² +6x + 8

Note that, for this introductory example, the value of a (the leading coefficient) is 1. When this is the case, you can factor the trinomial on the left-side of the equation as follows:

Figure 04: How to solve quadratic equations by factoring.

Step One: Identify the values of b and c.

In this example, the values of b and c are: b=6 & c=8

Step Two: Find two numbers that both ADD to b and MULTIPLY to c.

Once you have identified the values of b and c (6 and 8 respectively in this example), you can use trial-and-error to find two numbers that both add to the b term (6) and multiply to the c term (8). Another way to say this is: find two numbers with a sum of 6 and a product of 8.

For example, let’s say that you chose the numbers 5 and 1. In this case, 5+1=6, but 5x1≠ 8, so these two numbers would not work.

• 5 + 1 =6 (the value of b) ✓

• 5 x 1 ≠ 8 (the value of c) ✘

However, if you chose the numbers 2 and 4:

• 2 + 4 =6 (the value of b) ✓

• 2 x 4 = 8 (the value of c) ✓

Since the sum of 2 and 4 is 6 and the product of 2 and 4 is 8, you can found out that the factors of the trinomial x² + 6x + 8 are (x+2) and (x+4)

Step Three: Use your numbers from step two to write out the factors

In this case, you can conclude that the factors of x² + 6x + 8 are (x+2) and (x+4).

Figure 05: x² + 6x + 8 = (x+2)(x+4).

How do you know if you result is correct? You can check your answer by performing double distribution as follows:

• (x+2)(x+4) = x² + 2x + 4x + 7 = x² + 6x + 8

If the result is the same trinomial that you started with, then you know that your factors are correct.

Figure 06: How to Solve a Quadratic Equation by Factoring

Now we have a new equation:

• (x+4)(x+2)=0

This is not our final answer. To solve this quadratic by factoring, we have to take each factor, set it equal to zero, and solve to find our solutions as follows:

• x+4 = 0 → x = -4

• x+2 = 0 → x = -2

Figure 07: The final step is to set each factor equal to zero and solve.

Final Answer: The quadratic equation x² + 6x + 8=0 has a solution of x={-4,-2}.

This solution should make sense since we already knew from the graphing the parabola that this particular quadratic would equal zero at x=-4 and x=-2.

Now that Example #1 is complete, you know exactly how to factor quadratic equations and how to solve quadratic equations by factoring. However, the way that you factor will vary by problem as not all trinomials are factored the same way.

Below, you will find examples for how to solve a quadratic equation by factoring for three different occasions:

• when the leading coefficient a=1 (this applies to Example #1)

• when the leading coefficient a≠1

For a more in-depth review of factoring trinomials, we highly recommend visiting our popular Step-by-Step Guide to Factoring Polynomials. Otherwise, let’s continue on to learning how to factor quadratic equations when a=1.

---

How to Factor Quadratic Equations When a=1

For this first section, we will focus on how to factor a quadratic equation with a leading coefficient of 1 (as opposed to any other number). Figure 08 highlights the difference between a quadratic equation where a=1 and a quadratic equation where a≠1.

Figure 08: Make sure that you can recognize when a quadratic has a leading coefficient of one or not.

Example #2: Factor and Solve x² -2x -15 = 0

First, note that this quadratic equation is in the form ax² + bx + c = 0 since the equation could be rewritten as:

• x² + (-2x) + (-15) =0

However, for the sake of simplicity, we will keep it as:

• x² -2x -15 =0

Since a=1 in this example, we can solve this quadratic equation the same way we solved Example #1.

First, we can split the quadratic into two parts: the left-side of the equal sign and the right-side of the equal sign. Then we can attempt to factor the trinomial x² -2x -15 on the left-side.

Figure 09: How to Factor Quadratic Equations: Start by isolating the trinomial on the left-side of the equal sign.

Now, we can find the factors of x² -2x -15 as follows:

Step One: Identify the values of b and c.

In this example, the values of b and c are: b=-2 & c=-15

Step Two: Find two numbers that both ADD to b and MULTIPLY to c.

Once you have identified the values of b and c (-2 and -15 respectively in this example), you can use trial-and-error to find two numbers that both add to the b term (-2) and multiply to the c term (-15). Another way to say this is: find two numbers with a sum of -2 and a product of -15.

In cases like this example, you need two number that will multiply to a -15. Since the product of two negatives is always positive and the product of two positives is also always positive, your factors will include one positive number and one negative number.

After some trial-and-error, you will find that 3 and -5 work because:

• 3 + -5 = -2 (the value of b) ✓

• 3 x -5 = -15 (the value of c) ✓

Since the sum of 3 and -5 is -2 and the product of 3 and -5 is -15, you have found out that the factors of the trinomial x² -2x -15 are (x+3) and (x-5)

Step Three: Use your numbers from step two to write out the factors

In this case, you can conclude that the factors of x² -2x -15 are (x+3) and (x-5).

Figure 10: Factor the trinomial on the left-side of the equal sign.

From here, we have a new equation to deal with:

• (x+3)(x-5)=0

To find the solution(s) to the original quadratic equation, we have to take each factor, set it equal to zero, and solve for x as follows:

• x+3 = 0 → x = -3

• x-5 = 0 → x = 5

Figure 11: How to Solve a Quadratic Equation by Factoring

Final Answer: The quadratic equation x² - 2x - 15 =0 has a solution of x={-3,5}.

Now, let’s look at one more example of how to factor quadratic equations when the leading coefficient is 1.

---

Example #3: Factor and Solve x² + 4x = 12

Do you notice anything different about this next example?

The equation is not a quadratic (i.e. it is not in ax² +bx + c = 0 form). To get this equation into ax² +bx + c = 0, we will have to rearrange it, namely by subtracting 12 from both sides so that there is a zero on the right side of the equals sign as follows:

• x² + 4x = 12

• x² + 4x -12 = 12 -12

• x² + 4x -12 = 0

By rearranging the terms in this way, our new equation is a quadratic that is now in ax² +bx + c = 0 form, meaning that we can solve it by factoring.

Figure 12: How to Factor a Quadratic Equation

Now, we can find the factors of x² +4x -12 as follows:

Step One: Identify the values of b and c.

In this example, the values of b and c are: b=4 & c=-12

Step Two: Find two numbers that both ADD to b and MULTIPLY to c.

Once you have identified the values of b and c (4 and -12 respectively in this example), you can use trial-and-error to find two numbers that both add to the b term (4) and multiply to the c term (-12). Another way to say this is: find two numbers with a sum of 4 and a product of -12.

After some trial-and-error, you will find that 6 and -2 work because:

• 6 + —2 = 4 (the value of b) ✓

• 6 x —2 = -12 (the value of c) ✓

Step Three: Use your numbers from step two to write out the factors

In this case, you can conclude that the factors of x² + 4x -12 are (x+6) and (x-2).

Finally, we can find our solutions by solving

• (x+6)(x-2)=0

To find the solution(s) to the original quadratic equation, we have to take each factor, set it equal to zero, and solve for x as follows:

• x+6 = 0 → x = -6

• x-2 = 0 → x = 2

Final Answer: The quadratic equation x² + 4x - 12 = 0 has a solution of x={-6,2}.

The entire step-by-step process for solving this example is illustrated in Figure 12 above. Now let’s move onto learning bow to factor a quadratic equation when the leading coefficient is not equal to one.

---

How to Factor Quadratic Equations When a≠1

Example #4: Factor and Solve 2x² - x - 6 = 0

For the first example, we have to find the solutions to the quadratic equation: 2x² - x - 6 = 0.

Notice that, in this case, the leading coefficient a≠1 (in this example a=2).

We can still solve this quadratic equation by separating the left and right-side of the equal sign where the trinomial is on the left side and the zero is on the right side as shown in Figure 13 below.

Figure 13: How to Factor a Quadratic Equation when a≠1

Now, we have to find the factors of the trinomial 2x² - x - 6 on the left-side of the equal sign as follows:

Figure 14: How to factor a trinomial a≠1

Factoring these types of trinomials is a bit more involved.

First, notice that you can not pull out a greatest common factor (GCF). When this is the case, you can use the AC method for factoring trinomials of the form ax² + bx + c when a≠1 as follows:

Step One: Identify the values of a and c and multiply them together

For this example, a=2 and c=-6…

• a x c = 2 x -6 = -12

Step Two: Factor and replace the middle term

Next, you have to take the resulting product from Step One (-12) and use it as a replacement for the middle term.

This means that you are replacing the middle term, -1x, with -12x, which we then have to factor as follows:

• -12 = -4 x 3; and

• -4 + 3 = -1

We chose -4 and 3 as factors because the sum of -4 and 3 equals negative 1, so we can rewrite the original trinomial as 2x² - 4x +3x - 6, as shown in Figure 15 below.

Figure 15: How to use the AC method to factor

Step Three: Split the new polynomial down the middle and take the GCF of each side

Our new polynomial is equivalent to the one that we started with, but now it has four terms: 2x² - 4x + 3x - 6

Now, you must split the polynomial down the middle to essentially create two separate binomials that you can simplify by dividing GCF’s out of as follows:

• First Binomial: 2x² - 4x = 2x(x-2)

• Second Binomial: 3x - 6 = 3(x-2)

This process of splitting the polynomial down the middle is illustrated in Figure 16 below.

Figure 16: Split the new polynomial down the middle and take the GCF of each side

Step Four: Identify the Factors

Lastly, you can now determine the factors.

The result from the previous step was 2x(x - 2) + 3(x -2). Within this expression you will find your two factors, (2x+3) and (x-2), as shown in Figure 17 below.

Figure 17: How to Factor Quadratic Equations

And now, you can conclude that the factors of 2x² - x - 6 are (2x+3) and (x-2).

Unfortunately, you still have to set these factors equal to zero and solve for x to find the solution to the original quadratic equation as follows:

• 2x + 3 = 0 → 2x = -3 → x = -3/2

• x-2 = 0 → x = 2

Final Answer: The quadratic equation 2x² - x - 6 = 0 has a solution of x={ -3/2 , 2 }.

The complete step-by-step process for solving this final example is illustrated in Figure 18 below.

Figure 18: How to Factorize Quadratic Equations

---

Conclusion: How to Solve Quadratic Equations by Factoring

Learning how to factor quadratic equations is a key algebra skill that can be learned with practice.

While many students will initially learn how to solve quadratic equations by graphing, the next step will be to learn how to solve quadratic equations by factoring, which means that you will have to know how to factor quadratic of the form ax² + bx + c = 0 when a=1 and when a≠1.

In this step-by-step guide to factoring quadratic equations, we covered both cases as we worked through several examples of factoring quadratics of the form ax² + bx + c = 0. Remember that not all questions will be directly in this form, but they can often be rearranged (i.e. they can be rewritten as an equivalent equation that is in the form ax² + bx + c = 0).

If you are still confused about how to factor quadratic equations, we highly recommend that you go back and work through all of the example problems above, carefully following each step. The more experience that you have working on these types of problems, the easier they will become.

Keep Learning:

How to Factor Polynomials (Free Step-by-Step Guide)

Learn how to factor binomials, trinomials, and cubic expressions.

---

How to Simplify Fractions in 3 Easy Steps

How to Simplify Fractions in 3 Easy Steps

Math Skills: How to simplify fractions, How to simplify a fraction by finding a greatest common factor

Learn How to Simplify Fractions in 3 Easy Steps

One of the most important math skills related to fractions is understanding how to simplify fractions.

While simplifying fractions can seem tricky at first, it is a math skill that most math students can master with a good amount of practice combined with a strong conceptual and procedural understanding of fractions.

This free Step-by-Step Guide on How to Simplify Fractions will teach you everything you need to know about simplifying fractions, including proper fractions, improper fractions, and mixed fractions. Together, we will use a simple 3-step process for simplifying fractions that you can use to solve any problem where you have to simplify a fraction!

You can use the quick-links below to jump to any section of this guide, or you can continue on and follow it step-by-step:

• Fraction Review and Key Vocabulary

• What Does it Mean to Simplify a Fraction?

• How to Simplify Fractions in 3 Easy Steps

Before we start working on any practice problems, let’s do a quick review of some important math vocabulary terms related to fractions that you will need to understand well to make the most out of this guide.

Fractions Review: Definitions and Vocabulary

Before you learn how to simplify fractions, it’s important that you have a strong foundational understanding of what fractions are in general.

For starters, let’s review the difference between the numerator of a fraction and the denominator of a fraction. The numerator of a fraction is the top number and the denominator of a fraction is the bottom number. For example, the fraction 3/5 has a numerator of 3 and a denominator of 5.

In this guide, whenever we reference the numerator of a fraction, we are talking about the top number. Conversely, whenever we reference the denominator of a fraction, we are talking about the bottom number.

Figure 01: The fraction 3/5 has a numerator of 3 and a denominator of 5

Next, let’s recap the difference between the three types of fractions:

• Proper Fractions

• Improper Fractions

• Mixed Fractions

Proper Fractions

Definition: A proper fraction is a fraction with a numerator that is smaller than the denominator. For example, 3/8 is a proper fraction because 3 < 8. The value of a proper fraction is always less than one whole.

• Examples: 3/8, 1/2, 7/9

Improper Fractions

Definition: An improper fraction is a fraction with a numerator that is greater than the denominator. For example, 7/5 is a proper fraction because 7 > 5. The value of an improper fraction is always greater than one whole.

• Examples: 5/2, 12/11, 9/4

Mixed Fractions

Definition: A mixed fraction is a fraction that is a combination, or sum, of a whole number and a proper fraction. For example, 4 1/2 is a mixed fraction that represents the sum of 4 and 1/2.

• Examples: 3 1/3, 7 5/8, 2 3/4

Figure 02 below illustrates examples of these three types of fractions.

Figure 02: What is the difference between a proper fraction, an improper fraction, and a mixed fraction?

Note that this guide will only focus on teaching you how to simplify a fraction that is proper.

---

What Does it Mean to Simplify a Fraction?

When we refer to simplifying fractions, we are talking about taking a fraction and reducing it down to its simplest form.

Note that not all fractions can be simplified. If the numerator and the denominator of a fraction have no common factors other than 1, then the fraction is already in simplest form and, thus, can’t be simplified. Whenever we have to simplify a fraction, you are trying to reduce it down to the point where it can no longer be simplified.

The act of simplifying a given fraction down to its most reduced form the is main objective of this guide. Whenever we simplify a fraction, we are not changing the value of the fraction. Rather, we are rewriting a new equivalent fraction that is in its simplest form (i.e. he numerator and the denominator of a fraction have no common factors other than 1).

Does this sound confusing? If so, a simple example may help. Let’s consider the fractions 1/2 and 3/6.

Figure 03: The fractions 3/6 and 1/2 are equivalent.

Figure 03 above compares the fractions 1/2 (one-half) and 3/6 (three-sixths).

We should already know that 1/2 and 3/6 are equivalent since each represent one half (i.e. one is half of two and three is half of six).

Simplifying fractions means reducing the fraction to its most reduced form whenever possible.

We can say that a fraction is in its simplest form if both the numerator and the denominator have no common factors other than 1. This is the case for 1/2, since 1 and 2 do not have any common factors other than 1, meaning that 1/2 is in its lowest possible form and it’s the simplest way of expressing one half.

But what about 3/6? Let’s consider the factors of the numerator 3 and the denominator 6:

• Factors of 3: 1, 3

• Factors of 6: 1, 2, 3, 6

Both 3 and 6 share a common factor of 3. So, if we can divide both the numerator and the denominator by 3 to find a new equivalent fraction that is in simplified form (which we already know should be 1/2). Let’s go ahead and do the math to see if our result checks out:

• 3/6 → (3 ÷ 3) / (6 ÷ 3) = 1/2

As expected, our result is 1/2. This way of mathematically proving that 3/6 and 1/2 are equivalent fractions and that 1/2 is the most simplified form of 3/6 is illustrated in Figure 04 below. The strategy that we used will serve as the basis for the 3-step method for simplifying fractions that you will learn in the next section.

Figure 04: The simplest form of a fraction is equivalent to the original fraction.

Before moving on, the key takeaway here is that any fraction in simplest form will be equivalent to whatever fraction you started with. However, this new simplified fraction is in its lowest form and can not be simplified further. For example, 3/5 is in simplest form because 3 and 5 do not share a greatest common factor other than 1.

Now let’s move onto working through some sample problems using a simple 3-step process for how to simplify fractions.

---

How to Simplify Fractions (Proper Fractions)

Example #1: Simplify: 8/32

To solve this first example as well as any problem where you have to simplify a fraction, we will use the following 3-step method for simplifying fractions:

1. Step One: List the factors of both the numerator and the denominator

2. Step Two: Determine the value of the greatest common factor shared by both the numerator and the denominator

3. Step Three: Divide both the numerator and the denominator by the greatest common factor to find a new equivalent fraction that is in simplest form.

Let’s go ahead and apply these three steps to the fraction 8/32 as follows:

Step One: List the factors of both the numerator and the denominator.

For this first step, we will list out all of the factors of 8 (the numerator) and 32 (the denominator) as follows:

• Factors of 8: 1, 2, 4, 8

• Factors of 32: 1, 2, 4, 8, 16, 32

Step Two: Determine the value of the greatest common factor shared by both the numerator and the denominator

Notice that 8 and 32 have three shared common factors: 2, 4, and 8. However, the greatest common factor shared by 8 and 32 is 8.

• The greatest common factor shared by 8 and 32 is 8.

Figure 05: 8 and 32 share a greatest common factor of 8

Step Three: Divide both the numerator and the denominator by the greatest common factor to find a new equivalent fraction that is in simplest form.

For the final step, we have to divide both the numerator and the denominator by 8 as follows:

• 8/32 → (8 ÷ 8) / (32 ÷ 8) = 1/4

Our result, 1/4 is in simplest form because both 1 and 4 do not share any factors other than 1, so we can conclude that:

Final Answer: The fraction 8/32 can be simplified to 1/4.

That’s all there is to it! Go ahead and review the Example #1 recap shown in Figure 06 below before moving onto the next example.

Figure 06: How to Simplify Fractions in 3 Easy Steps.

---

How to Simplify a Fraction Example #2: Simplify: 18/27

Just like the previous example, we will again use our 3-step method to simplify the fraction 18/27 as follows:

Step One: List the factors of both the numerator and the denominator.

First, let’s list all of the factors of 18 and 27:

• Factors of 18: 1, 2, 3, 6, 9, 18

• Factors of 27: 1, 3, 9, 27

Step Two: Determine the value of the greatest common factor shared by both the numerator and the denominator

In this case, 18 and 27 share a greatest common factor of 9.

Figure 07: How to Simplify a Fraction: Start by finding the greatest common factor shared by the numerator and the denominator.

Step Three: Divide both the numerator and the denominator by the greatest common factor to find a new equivalent fraction that is in simplest form.

Finally, the last step is to divide both the numerator and the denominator by 9:

• 18/27 → (18 ÷ 9) / (27 ÷ 9) = 2/3

The resulting fraction, 2/3, is in simplest form because both 2 and 3 do not share any factors other than 1.

Final Answer: The fraction 18/27 can be simplified to 2/3.

Our entire approach to solving Example #2 is recapped in Figure 08 below.

Figure 08: How to Simplify a Fraction

Now, let’s work through one more example of how to simplify a fraction that is proper.

---

How to Simplify Fractions Example #3: Simplify: 66/93

We can simplify 66/93 using our 3-step process as follows:

Step One: List the factors of both the numerator and the denominator.

Start by listing all of the factors of 66 and 93:

• Factors of 66: 1, 2, 3, 6, 11, 22, 33, 66

• Factors of 93: 1, 3, 31, 93

Step Two: Determine the value of the greatest common factor shared by both the numerator and the denominator

Now that all of the factors are listed, we can see that 66 and 93 share a greatest common factor of 3.

Figure 09: 66 and 93 share a greatest common factor of 3.

Step Three: Divide both the numerator and the denominator by the greatest common factor to find a new equivalent fraction that is in simplest form.

For the final step, we have to divide both the numerator and the denominator by 3:

• 66/93 → (66 ÷ 3) / (93 ÷ 3) = 22/31

The result, 22/31, is in simplest form because both 22 and 31 do not share any factors other than 1.

Final Answer: The fraction 66/93 can be simplified to 22/31.

Figure 10: How to simplify a fraction by finding a greatest common factor.

---

Conclusion: How to Simplify Fractions

Whenever you have to simplify a fraction, you have to reduce the fraction down to its simplest form, meaning that the new fraction’s numerator and denominator have no common factors besides 1.

When you simplify a fraction, you are finding a new reduced form fraction that is equivalent to the original fraction. For example, 3/6 can be simplified as 1/2 and both are equivalent to “one half".”

You can solve any problem where you have to simplify a fraction by following this easy 3-step method:

How to Simplify Fractions in 3 Easy Steps

1. Step One: List the factors of both the numerator and the denominator

2. Step Two: Determine the value of the greatest common factor shared by both the numerator and the denominator

3. Step Three: Divide both the numerator and the denominator by the greatest common factor to find a new equivalent fraction that is in simplest form.

To gain some more practice using these steps, we recommend that you go back and work through the practice problems in this guide on your own a second time or to work on some of the free Simplifying Fractions Worksheets available on our math worksheet libraries page.

Keep Learning:

How to Subtract Fractions in 3 Easy Steps (free Step-by-Step Guide for Students)

---

Search Tags: how to add fractions, how to add fractions with different denominators, how to add fraction , how to add fractions with unlike denominators, how to. add fractions, how to add fractions with, how to add a fraction

11 Inspiring Growth Mindset Quotes for All Ages

11 Inspiring Growth Mindset Quotes for All Ages

The Best Quotes About Growth Mindset of All Time

Looking for inspirational growth mindset quotes? (Image: Mashup Math MJ)

Are you looking for a collection of the top 11 quotes about growth mindset?

If so, you’re in the right place. This post shares 11 of the most inspiring growth mindset quotes of all time, many of which you will inspire you to take on new challenges and to learn new things.

With a growth mindset for learning you view mistakes as learning opportunities, persevere through challenges, and value personal growth over end results. But nurturing a growth mindset takes time and consuming the right types of messages on a consistent basis is a great strategy for keeping you on the right path.

View fullsize

Click here to learn more about the difference between a growth mindset and a fixed mindset for learning.

One great way to keep yourself motivated along your journey of developing a growth mindset is to have access to inspirational growth mindset quotes from successful individuals whom you admire. These role models can help you to see the power of developing a growth mindset for learning and how long-term success often depends on one’s ability to learn from their mistakes and embrace challenges head-on.

Below you will find 10 of our favorite quotes about growth mindset. This collection of growth mindset quotes features men and women from a variety of backgrounds and careers, so you will surely find a few that will be inspirational and motivational.

11 Inspirational Growth Mindset Quotes

Quotes about Growth Mindset #1: Carol Dweck

The passion for stretching yourself and sticking to it, even (or especially) when it’s not going well, is the hallmark of the growth mindset.

-Carol Dweck

The first entry on our list of growth mindset quotes comes Stanford professor and growth mindset pioneer Carol Dweck. (Image: Mashup Math MJ)

---

Quotes about Growth Mindset #2: Albert Einstein

It’s not that I’m so smart, it’s just that I stay with problems longer.

-Albert Einstein

The second entry on our list of growth mindset quotes comes from the great Albert Einstein. (Image: Mashup Math MJ)

---

Quotes about Growth Mindset #3: Oprah Winfrey

I’ve come to believe that each of us has a personal calling that’s as unique as a fingerprint, and that the best way to succeed is to discover what you love and then find a way to offer it to others in the form of service, working hard, and also allowing the energy of the universe to lead you.

-Oprah Winfrey

Our third inspirational growth mindset quote comes from Oprah Winfrey. (Image: Mashup Math MJ)

---

Quotes about Growth Mindset #4: Michael Jordan

I can accept failure, everyone fails at something. But I can’t accept not trying.

-Michael Jordan

This growth mindset quote from Michael Jordan is one of the best of all time! (Image: Mashup Math MJ)

---

Quotes about Growth Mindset #5: Steve Jobs

Sometimes when you innovate, you make mistakes. It is best to admit them quickly, and get on with improving your other innovations.

-Steve Jobs

Our next growth mindset quote comes from Apple Cofounder Steve Jobs. (Image: Mashup Math MJ)

---

Quotes about Growth Mindset #6: Bruce Lee

Persistence, persistence, and persistence. The Power can be created and maintained through daily practice—continuous effort.

-Bruce Lee

Our sixth inspirational growth mindset quote comes from martial artist Bruce Lee. (Image: Mashup Math MJ)

---

Quotes about Growth Mindset #7: Thomas Edison

Many of life’s failures are people who did not realize how close they were to success when they gave up.

– Thomas Edison

This inspirational growth mindset quote is by inventor Thomas Edison. (Image: Mashup Math MJ)

---

Looking for inspirational Growth Mindset Quotes to share with your kids?

Access over one hundred printable Growth Mindset quote posters for your classroom in our brand new PDF eBook!

---

Quotes about Growth Mindset #8: Ariana Grande

Learn from your mistakes. Take responsibility and forgive yourself.

-Ariana Grande

(Image: Mashup Math MJ)

---

Quotes about Growth Mindset #9: Pele

Success is no accident. It is hard work, perseverance, learning, studying, sacrifice, and most of all, love of what you are doing or learning to do.

–Pele

One of the best quotes about growth mindset comes from the great Pele. (Image: Mashup Math MJ)

---

Quotes about Growth Mindset #10: Lebron James

You can't be afraid to fail. It's the only way you succeed. You're not gonna' succeed all the time and I know that.

-Lebron James

One of our top growth mindset quotes comes from Lebron James. (Image: Mashup Math MJ)

---

Quotes about Growth Mindset #11: Mark Twain

 Twenty years from now you will be more disappointed by the things you did not do than by the ones you did. So… sail away from the safe harbor. Explore. Dream. Discover.

– Mark Twain

Our final growth mindset quote comes from famous American author Mark Twain. (Image: Mashup Math MJ)

---

Conclusion: Growth Mindset Quotes

Now that you have seen all 11 of our favorite inspirational growth mindset quotes, it should be clear that the art of learning from one’s mistakes, practicing persistence, and viewing personal growth as a lifelong journey is both a timeless and ageless pursuit. Each growth mindset quote serves as a strong reminder that your potential for growth has no limitations. As long as you are willing to give effort and not get discouraged by your mistakes, you will be able to learn and to grow.

In your everyday life, you can use these insights to supply you with inspiration and motivation as you take on new challenges and continue to develop your own growth mindset for learning. In doing so, you are making a commitment to becoming ever persistent, resilient, and a true lifelong learner.

If you would like to learn more about a growth mindset for learning and its incredible benefits, check out our in-depth article on Defining a Growth Mindset for Learning (and Why it Matters).

Is 0 a Whole Number? (Instant Answer)

Is 0 a Whole Number? Yes or No?

What is the definition of a whole number and is 0 a whole number?

Is 0 a Whole Number? (Image: Mashup Math MJ)

When learning about the different categories of numbers (natural numbers, whole numbers, integers, etc.), zero can sometimes get lost in the shuffle. Many students often wonder: “Is 0 a whole number?” If you are asking this question yourself, you can click here for an instant answer or you can read through this short guide for a complete explanation, which includes definitions to some important math vocabulary terms related to numbers.

Before we determine whether or not 0 is a whole number, let’s do a quick review of the difference between natural numbers and whole number in math.

Natural Numbers

In math, a natural number is a number that can be used for counting or ordering values or amounts. The set of natural numbers starts at 1 and continues as follows: { 1, 2, 3, 4, 5, 6, 7, …}

Notice that 0 is not included in this set and, thus, 0 is not a natural number.

Whole Numbers

In math, a whole number is any number that does not include fractions, decimals, or negatives. Another way to think about the set of whole numbers is a set that includes all of the positive integers as well as zero. The set of whole numbers starts at 0 and continues as follows: { 0, 1, 2, 3, 4, 5, 6, 7, …}

Notice that 0 is indeed included in this set and, thus, we can conclude that…

Figure 01: The Universe of Number: Is 0 a Whole Number?

Is 0 a Whole Number?

Instant Answer: Zero is a Whole Number

Yes, zero is a whole number.

Why? By definition, 0 is not included in the set of natural numbers (i.e. zero is not a natural number), but it is included in the set of whole numbers (i.e. zero is a whole number).

Additionally, 0 is the first whole number and is followed by 1, 2, 3, 4, 5, etc.

The graphic in Figure 02 below shows how zero is included in the set of whole numbers but not in the set of natural numbers.

Figure 02: The Universe of Number: Is 0 a Whole Number?

Zero's Important Place in the Number System

Why is zero such an important number when it comes to the universe of numbers? We have already established that, by definition, zero is a whole number. As far as values go, zero is unique because it represents the absence of value or a null quantity (i.e. zero represents nothing, which is why it is neither positive nor negative)

So, why is 0 a whole number? Because the concept of counting whole values relies on 0 to serve as a starting point (i.e. the point where you have nothing). Without this starting point, all non-zero whole numbers would lose their context.

If this explanation is hard to understand, we can think about zero’s role as a whole number from a practical standpoint. For example, if you were measuring the number of days that you visited the gym last year, you would rely on 0 to represent the instance where you never attended at all. Then, the remaining whole numbers could be used to determine how many times you actually attended. And since you can’t visit the gym negative times or a fraction/decimal of a time, the set of whole numbers would be used for this particular scenario.

Is 0 a Whole Number? Yes! (Image: Mashup Math FP)

More Key Facts About Zero

If you were surprised to find out that 0 is a whole number, then you may also be surprised by some other interesting and fundamental facts about zero.

Here are a few examples of some surprising facts about zero,

Zero is a whole number.

Is 0 a whole number? As previously stated, zero is, by definition, a whole number, meaning that it is included in the set of whole numbers {0, 1, 2, 3, 4, 5, …}

Zero is an integer.

Is 0 an integer? Since the set of integers includes all of the whole numbers and their negative counterparts, we can also say that zero is an integer as well.

Zero is neither negative nor positive.

Is 0 positive or negative? The set of integers includes every non-zero whole number and its negative counterpart as well as zero. This definition is worded this way because zero is the only integer that is neither negative nor positive. Zero is important in this sense because it is the “neutral value” that separates all of the positive numbers from the negative numbers.

Zero is an even number.

Is 0 even or odd? While you can’t divide a number by zero, you can divide zero by a number. By definition, a number is even if it can be divided by 2 without any remainder. Since 0/2 = 0, we can say that, by definition, zero is an even number (and that zero is not an odd number).

Conclusion: Is 0 a Whole Number?

If you find yourself wondering “Is 0 a Whole Number?”, then it’s important that you understand the mathematical definition of a whole number in the first place.

In math, a whole number is any number that does not include fractions, decimals, or negatives. And, since 0 does not include fractions or decimals and is not negative, we know that 0 is included in the set of whole number {0, 1, 2, 3, 4, 5, 6, 7, …}.

In short, the answer to the question “Is 0 a Whole Number?” is yes! By definition, zero is included in the set of whole numbers and it plays the important role of the absence of value or a null quantity. All of the non-zero whole numbers have a value that is determined based on its distance from zero on the number line. Pretty cool, right?

Additionally, while zero is not a natural number, it is all of the following:

• zero is a whole number

• zero is an integer

• zero is neither positive nor negative

• zero is an even number

Whether you came to this page looking for a simple yes or no answer or a deep exploration of the properties of 0, we hope that you leave here with a greater appreciation of 0 and its status in the universe of real numbers. As you continue to learn zero’s place in the number system, you will continue to gain a deeper understanding of mathematics and numbers in general.

---

More Free Resources You Will Love:

Image: Mashup Math MJ

Why Am I So Bad at Math? (And How to Get Better)

If you are wondering, why am I so bad at math? The fault is likely due to you having a fixed mindset for learning, which is often a product of being negatively affected by harmful misconceptions about your ability to learn math.

---