How to Find the Area of a Semicircle
Math Skills: How to Find the Area of a Semicircle Using 3 Simple Steps
Free Math Guide: How to find the area of a semicircle.
In math, it is important to understand how to find the areas of geometric shapes including triangles, rectangles, and circles. Once you understand how to find the area of the basic figures, you can extend that understanding to dealing with more complex figures such as parallelograms, trapezoids, and—the focus of this guide—semicircles.
What is a semicircle?
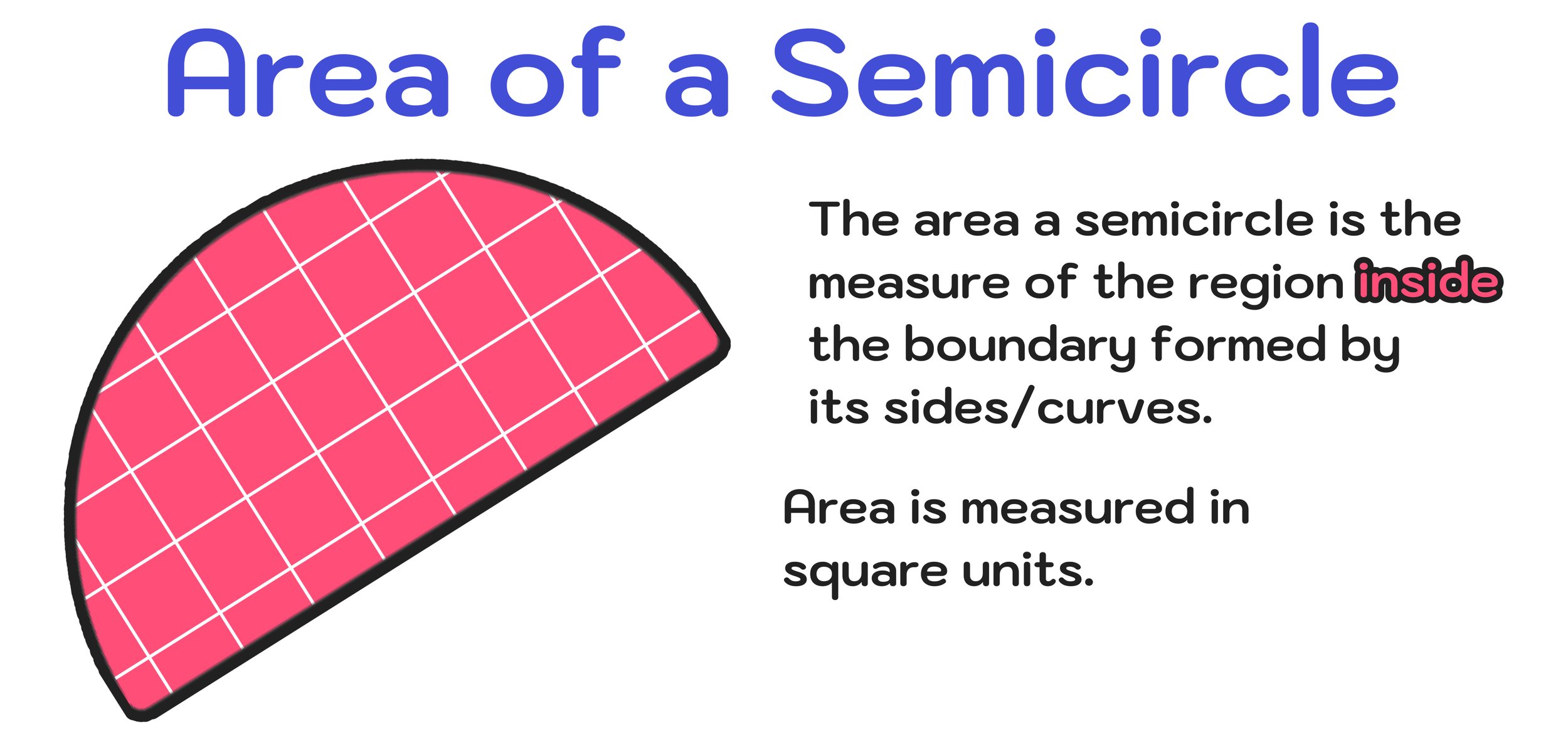
By definition, a semicircle is half of a circle. The area of a semicircle is the measure of the space contained within the semicircle, which is always expressed using square units.
(Are you looking for a free Area of a Semicircle Calculator? Click here to access our Area of a Semicircle Calculator)
This step-by-step guide on how to find the area of a parallelogram covers the following topics:
What is the Area of a Semicircle?
Figure 01: What is the area of a semicircle?
What exactly is the area of a semicircle? As previously stated, the area of a semicircle is just the measure of the region inside the boundary formed by its sides/curves. Additionally, the area of a semicircle (or any other two-dimensional geometric figure) is always measured in square units such as square inches, square yards, square miles, etc.
If you can find the area of a full circle, then you can easily find the area of a semicircle by applying one extra step (more on that in the next section).
To calculate the area of a semicircle, you only need to know the length of its radius in order to solve a problem. Once you know the length of the radius of a semicircle, you can use the area formula of a semicircle to calculate its area.
In the next section of our guide, we will learn how the formula for the area of a semicircle works and then we will move onto solving problems using a simple and easy three step process.
Let’s get started!
What is the Formula of a Semicircle Area?
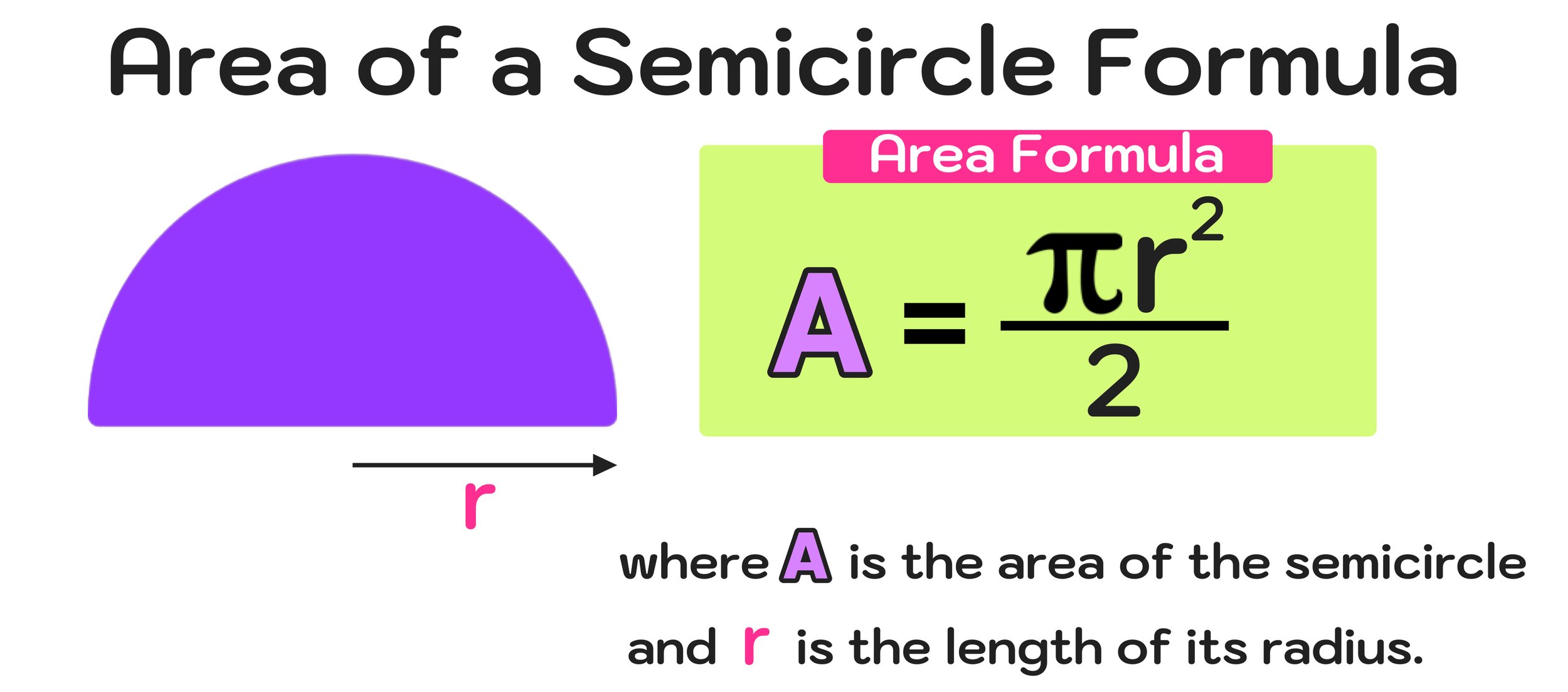
Figure 02: What is the area formula of a semicircle? The formula for the area of a semicircle is A=(𝝅r^2)/2
You can find the area of a semicircle, A, with a radius length of r by using the area of a semicircle formula: A=(𝝅r^2)/2
Remember that a semicircle is half of a circle. You probably already know that the formula for finding the area of a circle is A=𝝅r^2. So, it should make sense that the area of a semicircle formula is the just the circle area formula divided by two (or cut in half), since a semicircle will have half of the area of a full circle!
Area of a Circle: A=𝝅r^2
Area of a Semicircle: A=𝝅r^2 ÷ 2
How to Find the Area of a Semicircle in 3 Steps
Understanding how to calculate the area of a semicircle is a practical and useful geometry skill that you can perform easily just by knowing the formula of a semicircle area and how to use the following 3 step method for finding the area of any semicircle.
How to Find the Area of a Semicircle in 3 Steps:
Step One: Identify the length of the radius, r, of the semicircle.
Step Two: Substitute the value of r into the area formula of a semicircle, A = (𝝅r^2)/2 and solve for A
Step Three: Express your final answer in terms of square units
Next, let’s work through a simple example of how to find the area of a semicircle by following these three steps.
In this example, the semicircle that you have to find the area of has a radius of 8cm (as shown in the diagram in Figure 03 below).
Figure 03: How do you find the area of a semicircle with a radius of 8cm?
Step One: Identify the length of the radius, r, of the semicircle.
In order to find use the area formula of a semicircle in the second step, you need to know the value of r (the length of the semicircle’s radius). This problem told you that the semicircle has a radius of 8cm, so you can conclude that r=8 and move onto the next step.
Step Two: Substitute the value of r into the area formula of a semicircle, A = (𝝅r^2)/2, and solve for A
Next, substitute r=8 into the formula for the area of a semicircle, A=(𝝅r^2)/2
A = (𝝅r^2)/2 → A = (𝝅 x 8^2)/2 → A = 64𝝅/2 → A = 32𝝅 → A ≈ 100.5
Step Three: Express your final answer in terms of square units
The last step is to make a conclusion, or final answer, about the area of the semicircle question using appropriate units.
Final Answer: The area of a semicircle with a radius of 8cm is approximately 100.5 square centimeters.
Figure 04: How to find the area of a semicircle
Once you are able to follow the three steps for finding the area of a semicircle (just as we did in the previous example), you will be able to apply the method to solving any math problem that requires you to calculate the area of a semicircle (as long as you know the length of its radius).
To give you some more experience with applying the three steps for finding the area of a semicircle (and using the formula of a semicircle area), let’s move onto solving two more examples.
How to Find the Area of a Semicircle Examples
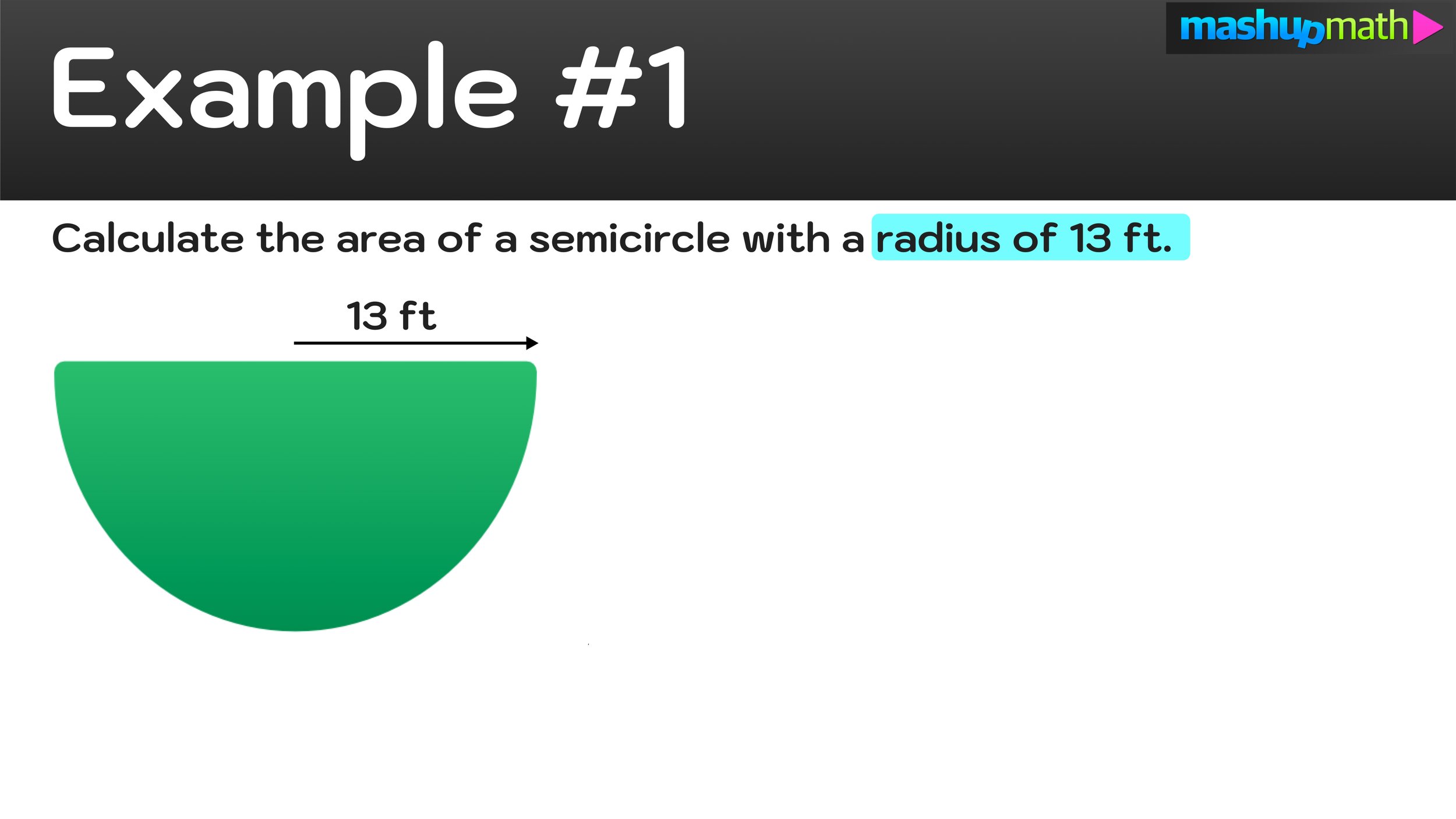
Example #1: Find the area of a semicircle with a radius of 13ft.
Example #1: Find the area of a semicircle with a radius of 13ft.
Calculating the area of a semicircle with a known radius length can be done easily by following the three step method that you learned about earlier:
Step One: Identify the length of the radius, r, of the semicircle.
In this first example, you know that the circle has a radius of 13 feet, so it’s easy to say that r=13
Step Two: Substitute the value of r into the area formula of a semicircle, A = (𝝅r^2)/2, and solve for A
Next, you can input r=13 into the area of a semicircle formula, A=(𝝅r^2)/2
A = (𝝅r^2)/2 → A = (𝝅 x 13^2)/2 → A = 169𝝅/2 → A ≈ 265.5
Step Three: Express your final answer in terms of square units
The third and final step is to determine your final answer in terms of square units
Final Answer: The area of a semicircle with a radius of 13ft is approximately 265.5 square feet (or 265.5 ft^2)
Example #1 Solved: Calculate the area of a semicircle with a radius of 13 feet
Example #2: Calculate the area of a semicircle with a diameter of 31 meters.
Example #2: Calculate the area of a semicircle with a diameter of 31 meters.
To solve Example #2 (or any other math problem that requires you to calculate the area of a semicircle), you can follow the same three steps as Example #1 as shown below:
Step One: Identify the length of the radius, r, of the semicircle.
Unlike Example #1, this problem does not directly tell you the length of the semicircle’s radius. Instead, the problem tells you that the semicircle has a diameter of 31 meters.
Remember that the radius of a circle is equal to half the measure of its diameter. So, to find the length of the radius of this circle, you simply have to divide it’s diameter by two as follows:
r = d/2 → r = 31/2 → r = 15.5
Since 31÷2=15.5, you can conclude that r=15.5 and then move onto the next step…
Step Two: Substitute the value of r into the formula for the area of a semicircle, A = (𝝅r^2)/2, and solve for A
For the next step, substitute r=15.5 into the area of a semicircle formula, A=(𝝅r^2)/2
A = (𝝅r^2)/2 → A = (𝝅 x 15.5^2)/2 → A = 240.25𝝅/2 → A ≈ 377.4
Step Three: Express your final answer in terms of square units
Finally, you can state your final answer using appropriate units as follows:
Final Answer: The area of a semicircle with a diameter of 15.5m is approximately 377.4 m^2
Example #2 Solved: The area of a semicircle with a diameter of 15.5m is approximately 377.4 square meters
Area of a Semicircle Calculator
Use our Free Area of a Semicircle Calculator to Make Instant Calculations
Are you in search of a tool that you can use to instantly calculate the area of any semicircle? If so, you can use our free Area of a Semicircle Calculator to solve problems and check answers.
To use our area of a semicircle calculator, just input the value of r (the radius of the semicircle) and press ENTER or DONE to get an instant answer—it’s that easy!
Click here to access our free Area of a Semicircle Calculator.
Conclusion: How to Find the Area of a Semicircle
You can calculate the area of any semicircle (half of a regular circle) with a known radius length, r, by using the area formula of a semicircle, A=(𝝅r^2)/2.
Calculating the area of a semicircle with a radius length or r can be done using a semicircle area calculator or manually, by following these three steps:
Step One: Identify the length of the radius, r, of the semicircle.
Step Two: Substitute the value of r into the area formula of a semicircle, A = (𝝅r^2)/2 and solve for A
Step Three: Express your final answer in terms of square units
More Math Resources You Will Love:
Search Tags: area of a parallelogram, how to find the area of a parallelogram, area of a parallelogram formula, how to find area of a parallelogram, area of a parallelogram calculator, find the area of a parallelogram, what is the area of a parallelogram, how do you find the area of a parallelogram, what is a area of a parallelogram, formula for area of a parallelogram, finding the area of a parallelogram, formula for the area of a parallelogram