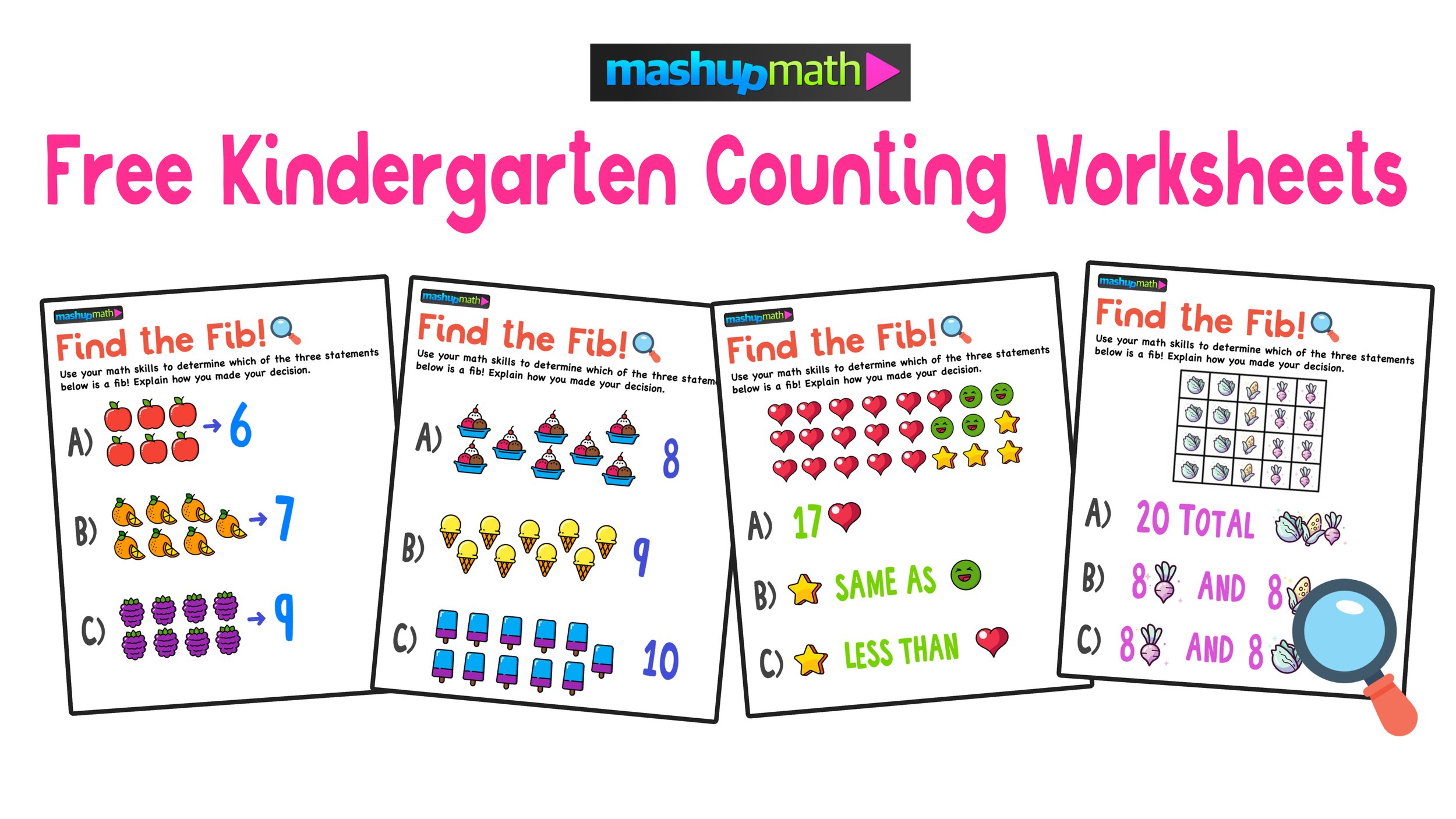
Hard Math Problems for 6th Graders: Pumpkins and Watermelons

Hard Math Problems for 6th Graders

Can Your 6th Graders Solve the Pumpkins and Watermelons Problem?

Hard Math Problems for 6th Graders: The Pumpkin and Watermelon Problem

Looking for more fun math riddles and brain teasers to share with your 6th graders? If so, then you will love today’s hard math problem, which is quite the brain bender.

Here is the problem, which involves figuring out the weights of pumpkins and watermelons:

Three pumpkins and two watermelons weigh 27.5 pounds. Four pumpkins and three watermelons weigh 37.5 pounds. Each pumpkin weighs the same as the other pumpkins. Each watermelon weighs the same as the other watermelons. How much does each pumpkin weigh? How much does each watermelon weigh?

Before we dive into solving this math problem, let’s talk about why these types of multi-step problems are considered hard math problems for 6th graders in the first place.

This math problem is not the typical type of problem that a 6th grade student will encounter, as the answer cannot be found in a direct or linear way. Also, the problem requires students to work with two different variables—pumpkins and watermelons, which is a much more challenging algebraic task than they may be used to.

However, this problem is appropriately challenging for 6th graders and they have the prerequisite skills to solve this problem using a variety of possible strategies. Once your 6th graders have found the relationship and the difference between the quantities, they can choose a strategy that they are comfortable with to determine the individual weight of a pumpkin and of a watermelon.

If you want to try to solve the problem for yourself, now would be the time to pause and try and solve it on your before continuing on to the answer.

Solution: How Much Does Each Item Weigh?

While there are many ways to solve this problem, we will offer one possible solution, which utilizes tape diagrams to help students visualize a very key piece of information—that the difference between the two statements:

• Three pumpkins and two watermelons weigh 27.5 pounds; and

• Four pumpkins and three watermelons weigh 37.5 pounds

—is that the combination of one pumpkin and one watermelon is equal to 10 pounds.

Once students figure this out, they can use this fact to isolate P in the 27.5 lb group and determine that the weight of one pumpkin is 7.5 pounds. They can then repeat this process again using the 27.5 lb group to determine that the weight of one watermelon is 2.5 pounds, as shown in the figure below.

View fullsize

Hard Math Problems for 6th Graders

Final Answer…

One pumpkin weighs 7.5 pounds and one watermelon weighs 2.5 pounds.

How did you and your students do with this problem? It surely was not easy, and it required your 6th graders to make sense of a complex problem that required multiple steps and some creative problem-solving techniques to get through.

Are you looking for more fun and challenging math activities, puzzles, and brain teasers to share with your 6th grade students? Check out our free math worksheet and activity libraries.

---

Do YOU Want More Fun Math Riddles, Puzzles, and Brain Teasers?

Wasn’t that fun? If you want to take on more brain-bending math puzzles to sharpen your mind and improve your problem-solving skills, check out the links below:

We Spent All Morning Working on This Rectangle Math Puzzle. Can You Solve It?

The controversial real answer is finally revealed. Can you solve it?

A Post By Anthony Persico

It’s no secret that we are obsessed with math riddles, puzzles, and brain teasers here at Mashup Math. Why? Because there are not many better feelings in life than finally reaching an aha moment after mulling over a brain-bending math brain teaser for a while (sometimes hours!) and figuring out the correct answer.

Like most math fans, we love problem-solving, and, like most math fans, we can be rather hardheaded when it comes to believing that our answer is correct and that any other answer is obviously wrong.

So, it was no surprise that a seemingly simple yet controversial math puzzle forced us to drop everything we were doing and spend an entire morning arguing about who had found the elusive right answer.

We have been sharing the rectangle math riddle with math fans for a while—well, sort of. The original math puzzle was nearly identical, except that it asks How Many Squares? (Not How Many Rectangles). This problem, shown below, is not too difficult to solve and it is appropriate for students at the elementary levels and above.

The Original Problem: How Many Squares?

When squares are involved, most people can figure out that the answer is 14 total squares.

(Hint: if you are unsure of how to solve the Squares Problem, remember that some of the squares are overlapping).

View fullsize

14 Total Squares

But What If I asked How Many Rectangles?

The How Many Squares Problem? is relatively simple and easy to solve. So, why does replacing Squares with Rectangles cause so much controversy?

This craziness all started when I received a text from a friend asking me if I had a quick math puzzle that I could send her to share with her son, a 4th-grade student, to try and solve before bed. With the How Many Squares? puzzle in mind, I quickly sketched the puzzle on a piece of lined paper using a Sharpie, took a picture with my phone, and sent it over to her. And, since I already had the picture, I also tweeted it out to all of our followers and went on with my evening.

This was the Tweet that launched a thousand different answers:

Got a number? pic.twitter.com/zTWl9WjOjW

— Mashup Math (@mashupmath) January 7, 2021

It wasn’t until the next morning that I saw that the tweet had over 200 replies and that I had accidentally asked How Many Rectangles? instead of How Many Squares?

And so, the controversy began.

Dozens of different solutions were being shared and several arguments breaking out.

I could have spent my entire day reading Twitter replies, but instead, I shared the puzzle with some friends who happen to be self-proclaimed Geometry wizards to see if there was a consensus solution. And I myself was on a quest to figure out why such a seemingly simple math puzzle had caused so much controversy.

Want to try the problem on your own? If so, don’t go any further. Stop here and try to solve the puzzle and come on back when you’re finished.

Gee, that was pretty quick! Are you ready to see the solution?

Unlike many popular math riddles and brain teasers that are purposely ambiguous and can have multiple answers, this math puzzle has one single, undeniable answer, and it’s 36 total rectangles.

Before we look at why 36 is the solution, let’s take a look at some of the most common responses on Twitter:

View fullsize

As you can see, there is a wide variety of answers and only a small percentage of people found the correct answer.

Some people even went as far as to claim that there are actually zero rectangles and blamed my inability to draw straight lines freehand…

I'll be sure to use a ruler next time.

Anyways, here is one more notable Tweet that will launch our discussion into why the actual answer is 36 rectangles:

How to Solve the Rectangles Math Riddle

Miri’s tweet is notable because she draws attention to a very important math fact that many people are forgetting or unaware of—that a square is a rectangle.

What!?

It’s true. By definition, a rectangle is a plane figure with four straight sides and four right angles, especially one with unequal adjacent sides.

And a square certainly fits this definition. In fact, a square a special kind of rectangle (check out the Is a Square a Rectangle? video below for a more in-depth explanation.

Now that we know that a square is a rectangle, we can use the same approach to How Many Squares? problem to solve the Rectangle Math Puzzle.

Here’s a handy diagram of how to find each possible rectangle:

Rectangle Math Puzzle Solution Breakdown

Start by counting all of the squares, in which there are 14 in total (shaded in pink). Did you remember to count the large perimeter square?

Squares: 14

Then move onto counting ALL of the rectangles:

1x3 Rectangles (Blue): 6

2x3 Rectangles (Green): 4

1x2 Rectangles (Orange): 12

Finally, find the sum of all of the rectangles:

14 + 6 + 4 + 12 = 36 Total Rectangles

---

Do YOU Want More Fun Math Riddles, Puzzles, and Brain Teasers?

Wasn’t that fun? If you want to take on more brain-bending math puzzles to sharpen your mind and improve your problem-solving skills, check out the links below:

The PEMDAS Rule Explained! (Examples Included)

The PEMDAS Rule Explained!

What is the PEMDAS Rule and how does it apply to the math order of operations?

A Post By Anthony Persico

What is the PEMDAS rule for math order of operations and solving problems? When studying math, you learn about a process called the order of operations. This process is a rule that must be followed when solving math problems that have multiple operations such as subtraction, addition, multiplication, division, groupings, and/or exponents.

There are many memory tricks for remembering the math order of operations in the correct order, but the most popular is the PEMDAS rule.

The PEMDAS Rule is a mnemonic that stands for:

View fullsize

P: Parenthesis

E: Exponents

M: Multiplying

D: Dividing

A: Adding

S=Subtracting

The operations included in the PEMDAS rule are performed left to right.

Additionally, the PEMDAS rule for recalling the math order of operations has a few important sub-rules that must also be followed if you want to use PEMDAS correctly (and get the correct answers to math problems). These important sub-rules relate to the relationships between multiplying/dividing and adding/subtracting.

These important PEMDAS rule sub-rules are explained in detail in the next section:

PEMDAS Rule: Key Points

The PEMDAS rule has been around for decades as a tool for helping students to remember the math order of operations. Many prefer to simply remember the mnemonic PEMDAS (pronounced PEM-DAHS), while others choose to remember the phrase Please Excuse My Dear Aunt Sally.

However, you choose to remember the PEMDAS rule is not as important as remembering the previously mentioned sub-rules? Why are the sub-rules to the PEMDAS rule so important? Because the sub-rules often make the difference between getting a correct or incorrect answer to a math problem.

The PEMDAS rule may not be perfect, but if you can remember the sub-rules, it can be a useful tool for helping you to correctly apply the math order of operations and getting correct answers on both simple and complex math problems provided that you know the important sub-rules.

Important Sub-Rules to the PEMDAS Rule:

1.) P: Perform operations inside of parenthesis or groups before you do anything else (if there are no groups or parentheses, you can skip this step).

2.) E: Next, after performing operations inside of parenthesis and groupings (if there are any), apply any exponents (if there are no exponents, you can skip this step).

3.) M/D: Next, after the parentheses and groups and the exponents, perform multiplying/dividing from left to right based on whichever operation is first).

★ Just because M comes before D in the PEMDAS rule doesn’t mean that you will always perform multiplication before division.

4.) A/S: Finally, after multiplying and/or dividing, perform adding/subtracting from left to right based on whichever operation is first).

★ Just because A comes before S in the PEMDAS rule doesn’t mean that you will always perform addition before subtraction

★ = Extremely Important

PEMDAS Rule Examples

Now that you know what the PEMDAS rule for remembering the math order of operations stands for, it’s time to learn how to use the rule to solve math problems and get correct answers.

Why? Because there is zero educational value in remembering what the PEMDAS rule stands for if you have no clue how to apply it to math order of operations.

Remember that the PEMDAS rule is only useful if you also remember the key sub-rules that were displayed in the last section.

With the sub-rules in mind, the next section will work through several examples of how to correctly apply the PEMDAS rule when it comes to math order of operations and problem-solving.

PEMDAS Rule Ex. 1: (3+1) x 4

First, solve whatever is in the groupings (parentheses):

3+1=4

Next, multiply: 4 x 4 = 16

Final Answer: 16

PEMDAS Rule Ex. 2: 27 ÷ (8-5)^2

 Again, perform operation inside of the groupings first.

Inside parentheses: 8-5 = 3.

The next step to evaluate the exponents: 3^2=9

The last step is to divide: 27÷9 = 3

Final Answer: 3

PPEMDAS Rule Ex. 3: 10 x 6 + 1

Notice that this example does not include groupings or any exponents. Therefore, you can skip the P and E in the PEMDAS rule and start with M/D.

Since multiplying/dividing comes before adding/subtracting, you can solve this problem by moving from left to right as follows:

 10x6 = 60

60 + 1 = 61

Final Answer: 61

PEMDAS Rule Ex. 4: 75 - 10 x 5

According to the PEMDAS rule, multiplying/dividing comes before adding/subtracting so you can NOT solve this problem by moving from left to right.

The PEMDAS rule requires you to multiply first and then perform subtraction second as follows:

10 x 5 = 50

75 – 50 = 25

Final Answer: 25

---

PEMDAS Rule Ex. 5: 8 x 8 ÷ 16

Are you ready to apply the important sub-rules?

Notice that there are only two operations in this math example: multiplication and division.

Before we move forward, let’s revisit sub-rule #3:

3.) M/D: Next, after the parentheses and groups and the exponents, perform multiplying/dividing from left to right based on whichever operation is first).

★ Just because M comes before D in the PEMDAS rule doesn’t mean that you will always perform multiplication before division.

In this problem, you can solve by performing multiplication fist (the left-most operation) and then division second as follows:

8 x 8 = 64.

64 ÷ 16 = 4

Final Answer: 4

Note: If you followed the PEMDAS rule strictly and solved from left to right, you could still have ended up with 4 as the correct answer. However, this will not always be the case as we will in the next example.

PEMDAS Rule Ex. 6: 42 ÷ 7 x 3

Let’s start by saying that many people will get this simple problem wrong because they forget the key sub-rules to the PEMDAS rule. They will make the mistake of strictly following the PEMDAS rule and performing multiplication before division (since M comes before D in PEMDAS).

Don’t make this mistake!

Remember that ★ Just because M comes before D in the PEMDAS rule doesn’t mean that you will always perform multiplication before division.

In this case, the only operations are multiplying and dividing. This time, division comes first, which is ok. You still solve the problem by moving from left to right as follows:

42÷7=6

6x3=18

Final Answer: 18

Why is 2 not the final answer? If you failed to apply the PEMDAS rule correctly, you may have made the mistake of performing multiplication before division as follows:

7 x 3 = 21

42 / 21 = 2 (THIS ANSWER IS WRONG!)

(Pro Tip: If this was a multiple-choice question, both 18 and 2 would both be choices. So, be careful!)

---

PEMDAS Rule: Why Is It Good to Know

It’s impossible to consistently solve math problems (both simple and complex) correctly without understanding how to apply the math order of operations and PEMDAS is an effective tool for recalling them in the right sequence—provided that you also remember the important sub-rules described above.

 The PEMDAS rule and the math order of operations have gained tons of attention in recent years because of viral social media posts sharing seemingly simple math problems that garner thousands of responses (and incorrect answers) due to the fact that many adults can remember “PEMDAS” but not how to apply the actual PEMDAS rule (and corresponding sub-rules).

Since many people can’t figure out the right answer to these simple problems, they are inclined to leave comments and tag friends, which only makes the most more popular on social media.

PEMDAS Rule for Math Order of Operations: Conclusion

The PEMDAS rule is a popular memory tool for recalling the math order of operations. The rule stands for P: Parenthesis, E: Exponents, M: Multiplying, D: Dividing, A: Adding, S=Subtracting.

In general, operations are performed from left to right, but there are very important key sub-rules, namely (1) perform multiplying/dividing from left to right based on whichever operation is first), and perform adding/subtracting from left to right based on whichever operation is first).

Without understanding these sub-rules, the PEMDAS rule becomes extremely unreliable and can lead you to get the wrong answers to simple math problems (see PEMDAS Rule Ex. 6 above).

PEMDAS may not be the best way to remember how to correctly apply the math order of operations, but it can be a reliable tool if and only if you also remember the key sub-rules as well.

---

The PEMDAS Rule is Good, but the GEMS Rule is Better!

Why is GEMS the Best Way to Teach Order of Operations?

View fullsize

---

More Free Math Resources for Grades K-8: