Converting CM to M: Everything You Need to Know
Are you looking to learn how to convert centimeters to meters (cm to m)?
Before you learn the absolute easiest way to convert cm into m (with and without a calculator), let’s do a quick review of some very important vocabulary terms (trust me, this will come in handy very soon):
Centimeter (cm) is a metric unit of length that equals one-hundredth of a meter.
Meter (m) is the fundamental unit of length in the metric system. Note that a meter is approximately 39.37 inches or 3 feet and 3 inches in the imperial system)
Note that the abbreviations for centimeters (cm) and meters (m) are meant to be expressed as lower-case letters.
The key takeaway from these definitions is that a meter is the standard unit of length in the metric system and that a centimeter is equal to one-hundredth of one meter (which means that there are one hundred centimeters in one meter). Centimeters are very small compared to meters, and:
One hundred centimeters make up one meter.
One meter is made up of one hundred centimeters.
Are you starting to see a relationship between centimeters and meters?
Figure 1: Centimeters Compared to Inches (image via Mashup Math FP)
Remember that meters and centimeters are metric system units of measurement (not imperial).
For reference, some things that measure approximately 1 meter are the width of a large refrigerator, the depth of the shallow end of a swimming pool, and the height of a typical kitchen countertop.
Figure 2: cm to m Relationship (image via Mashup Math FP)
If you can understand the relationship between cm and m (and m and cm) displayed in Figure 2, then you will be able to convert cm into m using the easy two-step method shown below!
Converting cm to m Examples
You can convert centimeters to meters by following these two easy steps.
(Note: First, you will learn how to convert cm into m by hand and then later on using a calculator).
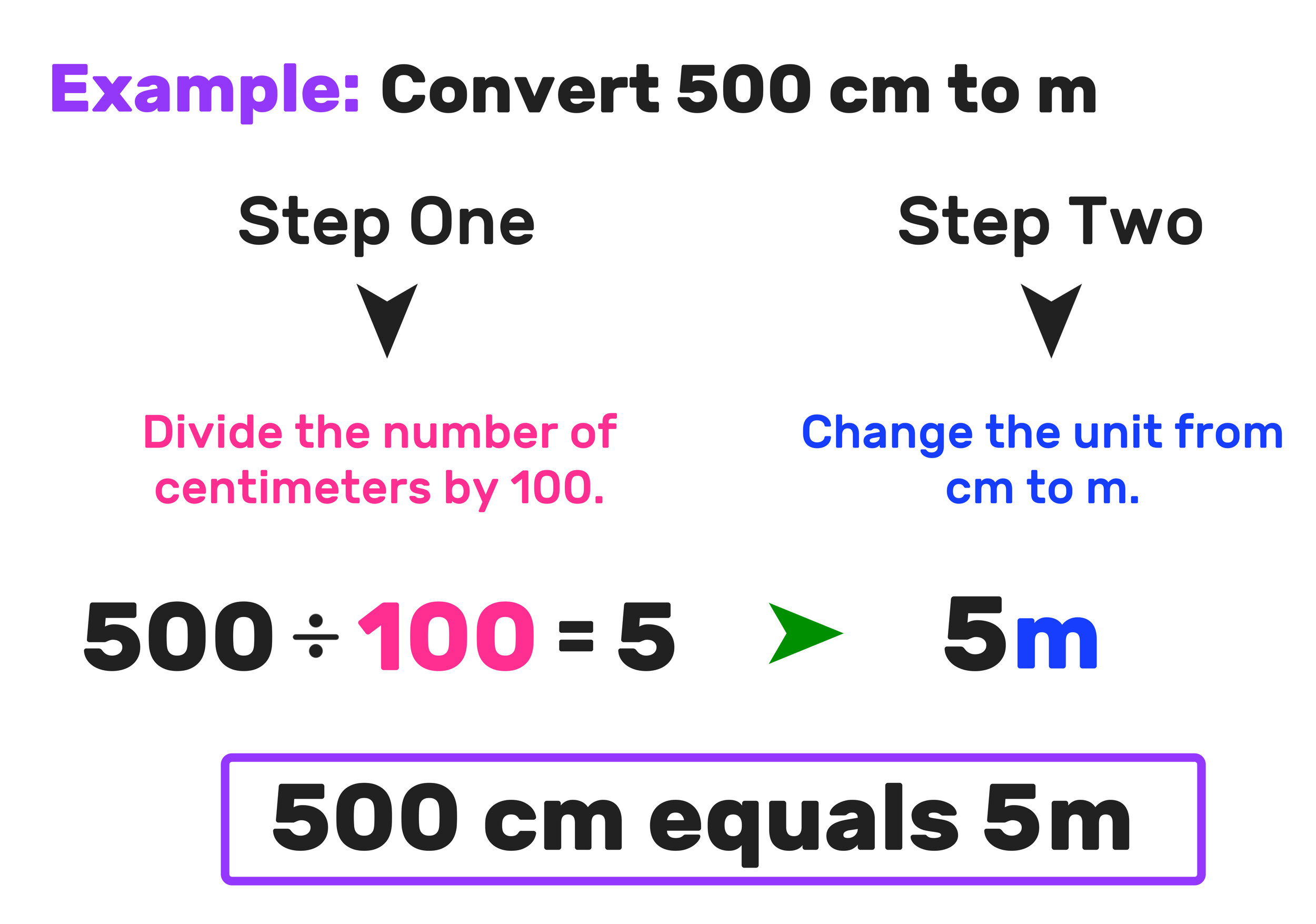
cm to m Example 01: Convert 500 cm to meters
Let’s start with a relatively simple example, where you have to convert 500 centimeters into meters.
Step One: Divide the Number of Centimeters by 100, as follows:
500 ÷ 100 = 5
Step Two: Change the Units to Meters
500 cm = 5 m
That’s it! (see Figure 3 for a more detailed explanation)
Final Answer: 500 centimeters equals 5 meters
Figure 3
By following the two simple steps above, you can always convert cm to m even if you don’t have a calculator. Now, let’s take a look at another example.
Here is another example of how to convert cm to m:
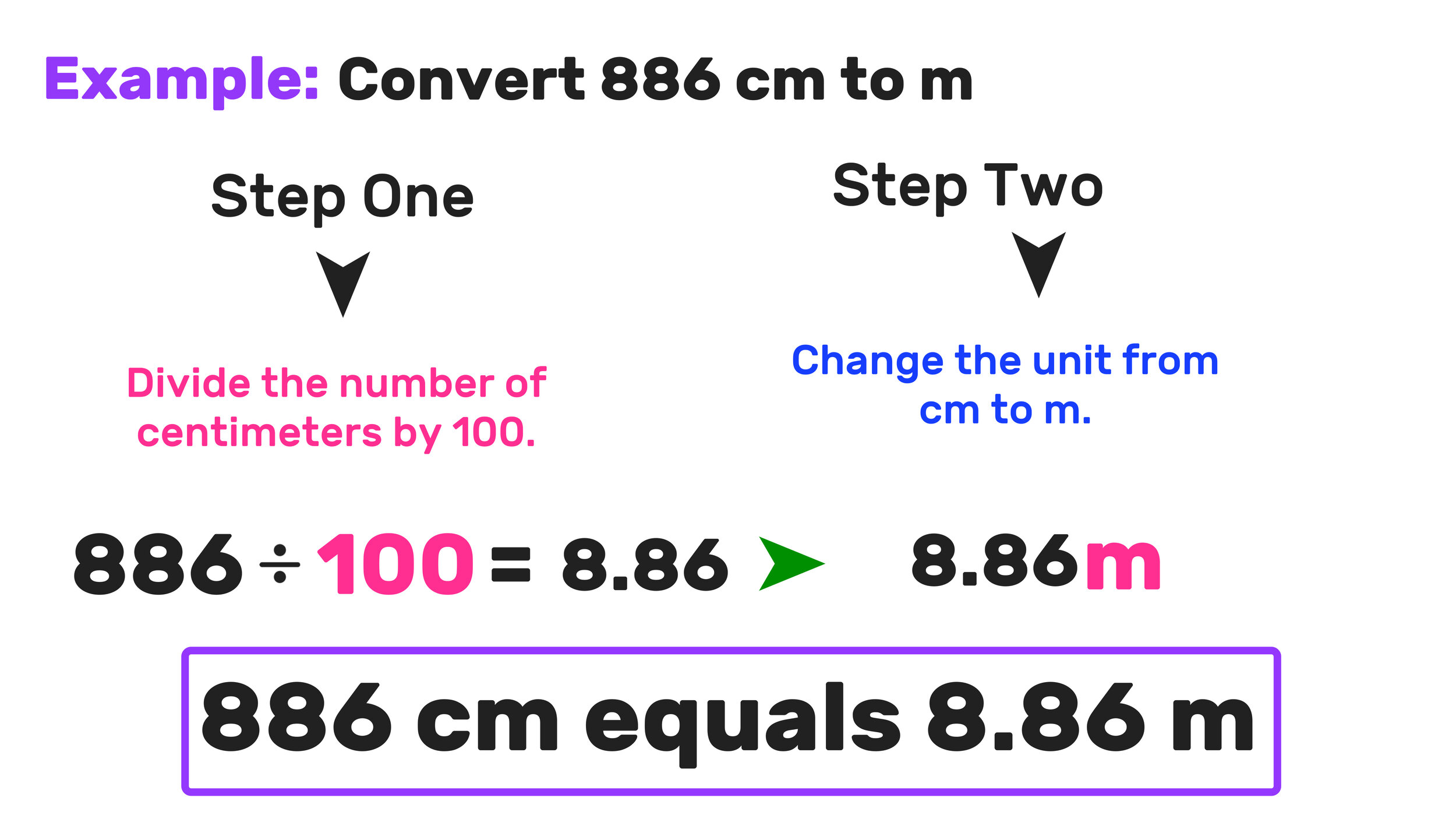
cm to m Example 02: Convert 886 centimeters into meters
In this example, you can convert cm to m using the same two-step method used in the previous example:
Step One: Divide the Number of Centimeters by 100, as follows:
886 ÷ 100 = 8.86
Step Two: Change the Units to Meters
886 cm = 8.86 m
Final Answer: 886 centimeters equals 8.86 meters
Figure 4. Notice that the answer to this example is a decimal, which is totally fine.
What if you flip cm to m?
Before you move onto learning about the cm to m calculator and trying some free practice problems, let’s take a super quick look at the relationship between the reverse of cm to m: converting meters into centimeters.
As you may have predicted, the conversions between cm and m are reversible. When going form cm to m, you divide by 100. When going in reverse, from m to cm, you multiply by 100.
Fun Fact: If you start with meters and convert to centimeters and then convert back to meters, or vice versa, you will end up with the same number that you started with (some students like to perform these calculations to check that their work is correct).
Example 03: Convert 8.86 meters into centimeters
Notice that this example is the reverse of Example 02 and you have to convert to m into cm. If the fun fact is true, then the final answer has to be 886 centimeters. Let’s see if it works out:
Step One: Multiply the Number of Meters by 100, as follows:
8.86 x 100 = 886
Step Two: Change the Units to centimeters
886 cm = 8.86 m
Final Answer: 8.86 meters equals 886 centimeters
Pretty cool, right?
Figure 5
cm to m Calculator
Screenshot from calculatorsoup.com
If you need a fast and easy way to convert between different units of measurement, including centimeters to meters (cm to m), then you can take advantage of the many free online centimeters to meters conversion calculators that are available.
This free distance conversion calculator from www.calculatorsoup.com will quickly make conversions from cm into m and vice versa, but it will not show you any of the work or the previously mentioned two-step process. While this cm to m calculator is a handy tool, it will not help you understand the process behind making distance conversions or the relationship between centimeters and meters.
To use the cm to m calculator, simply input the number of centimeters in the Value to Convert box and choose to convert from centimeters to meters. If you do not input the numbers correctly, you will not get a correct cm to m conversion.
Converting cm to m Practice Problems
Looking for some extra practice converting cm into m (and m into cm)?
The following centimeters to meters practice problems will give you plenty of opportunities to apply the two-step process to converting cm to m or to use a cm to m calculator to make conversions. There is also an answer key at the bottom of this post.
1.) Convert 1,000 cm to m
2.) Convert 2,100 cm to m
3.) Convert 55 m to cm
4.) Convert 3.75 m to cm
5.) Convert 10,222 cm to m
6.) Convert 0.5 m to cm
7.) Convert 1 Million cm to m
8.) Convert 0.01 m to cm
9.) Convert 774 cm to m
10.) Convert 6 Billion cm to m
And if you are looking for some real-world practice problems involving measurement conversions, including converting cm to m, check out this free measurement conversion video lesson:
Answer Key:
1.) 10m
2.) 21 m
3.) 5,500 cm
4.) 375 cm
5.) 102.22 m
6.) 50 cm
7.) 10,000 m
8.) 1 m
9.) 7.74 m
10.) 10 million m
More Free Decimals and Fractions Resources:
Keep Learning:
Share your ideas, questions, and comments below!
(Never miss a Mashup Math blog--click here to get our weekly newsletter!)
By Anthony Persico
Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.