Free Fraction Chart (Printable PDF)

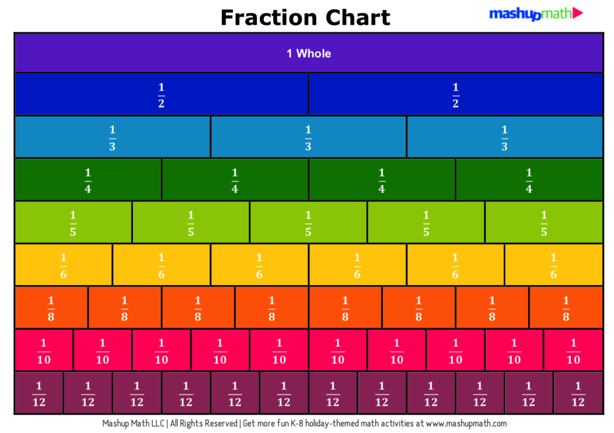
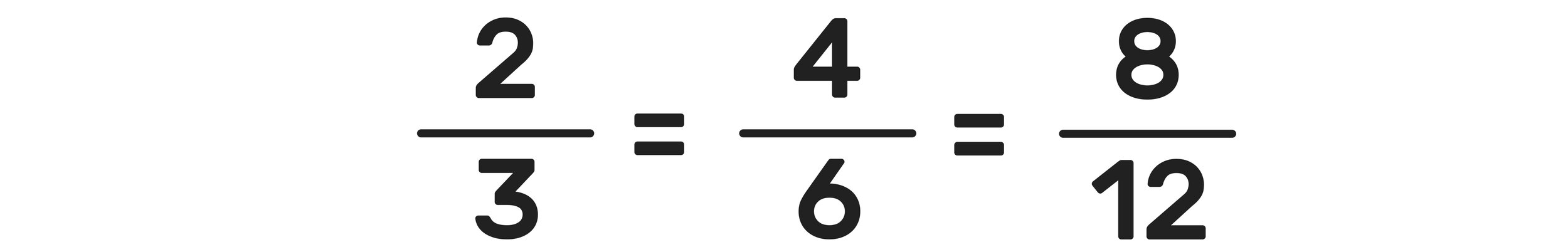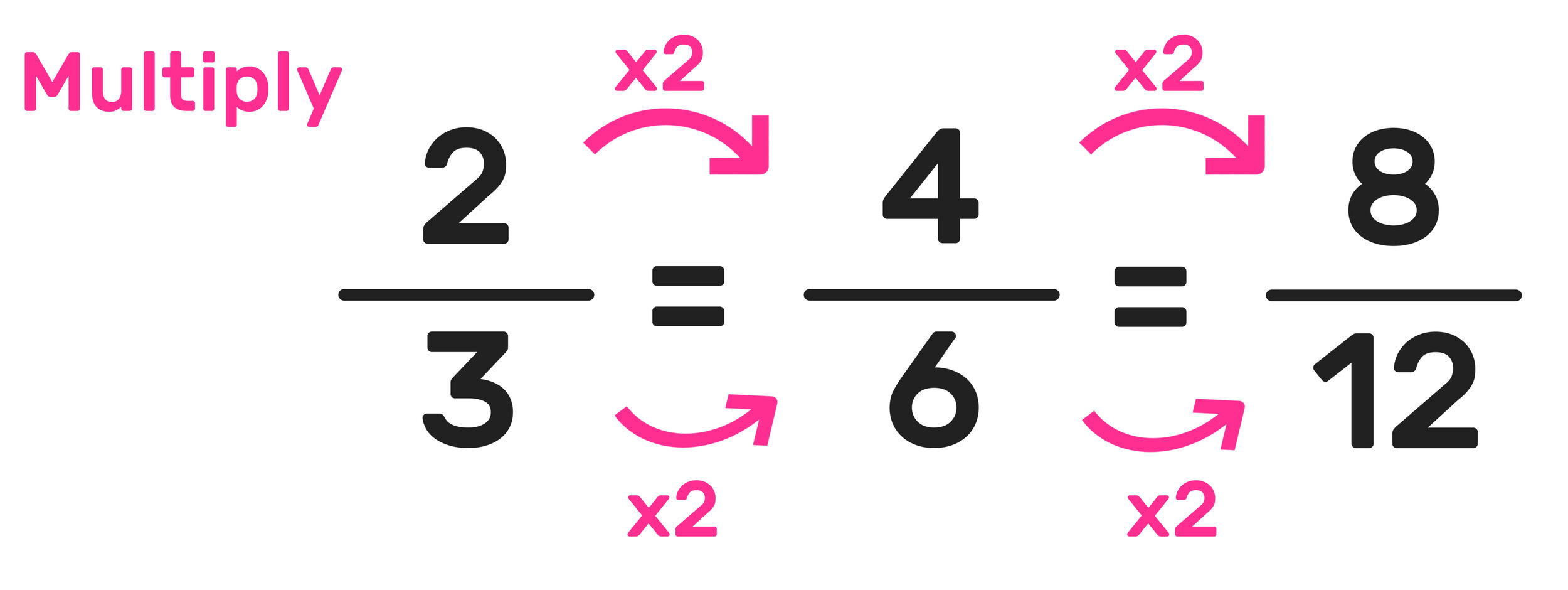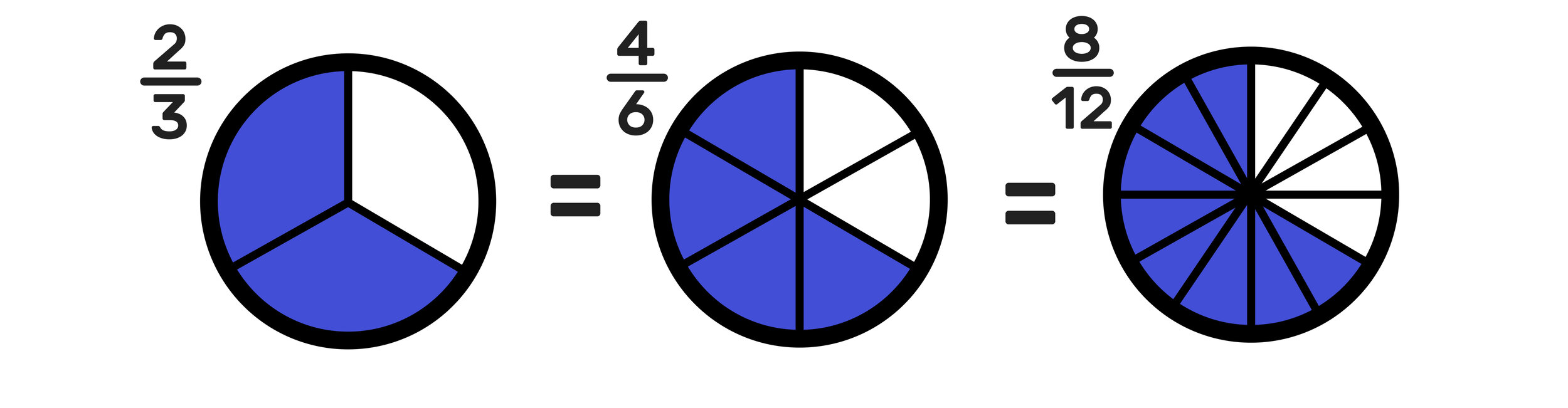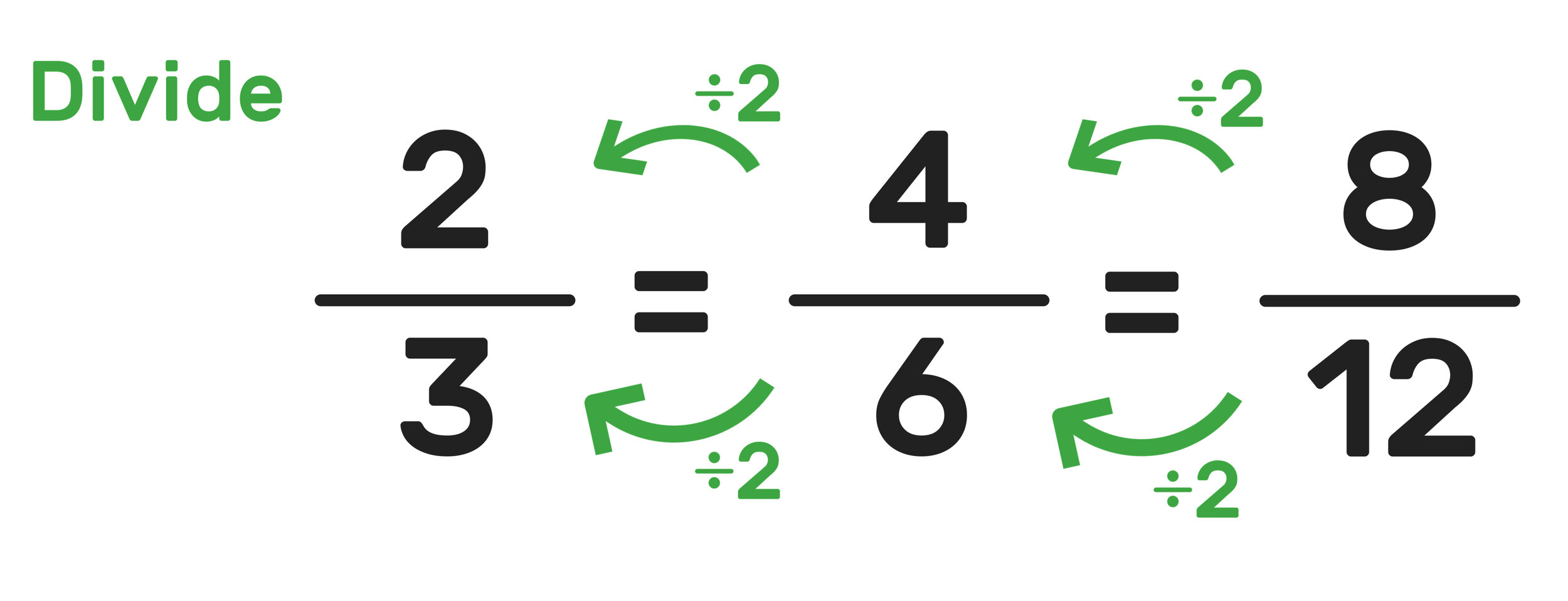Free PDF Fraction Chart (Equivalent Fractions)

Are you looking for a useful reference chart for comparing and identify equivalent fractions?

If so, click the link below to download your free fraction chart as an easy to share and print pdf file.

Need extra practice or help working with Equivalent Fractions? Check out this free Equivalent Fractions Explained! lesson guide.

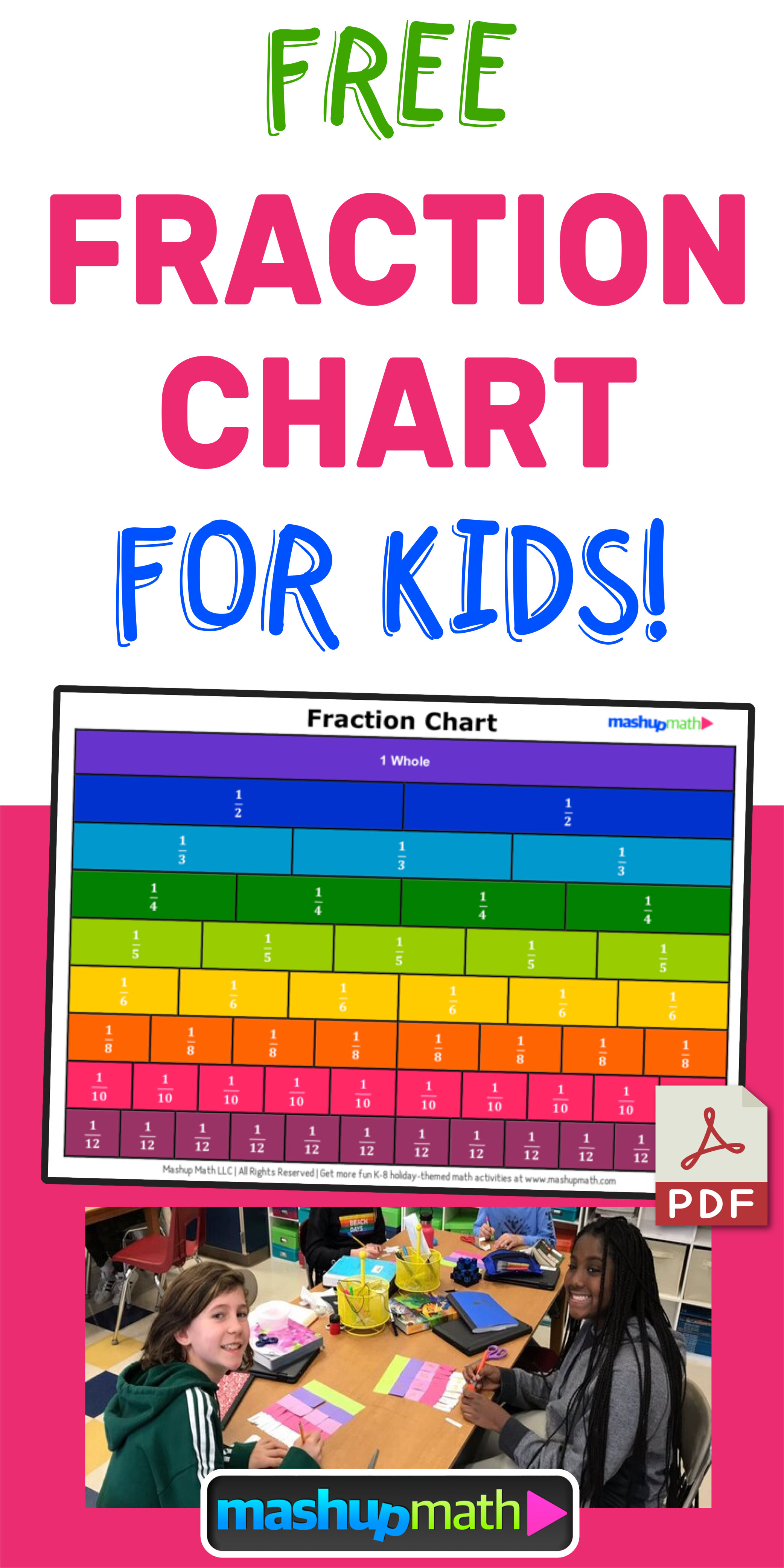
Free PDF Fraction Chart!

⤓ Download Your Free Fraction Chart PDF

---

Activity Idea: Fraction Kits

Are you looking for strategies to help your kids understand equivalent fractions this school year?

Creating fraction kits is a great way to get your kids exploring equivalent fractions and acquiring a deep, conceptual understanding of the topic.

Click here to learn more about this activity and to see a video tutorial!

---

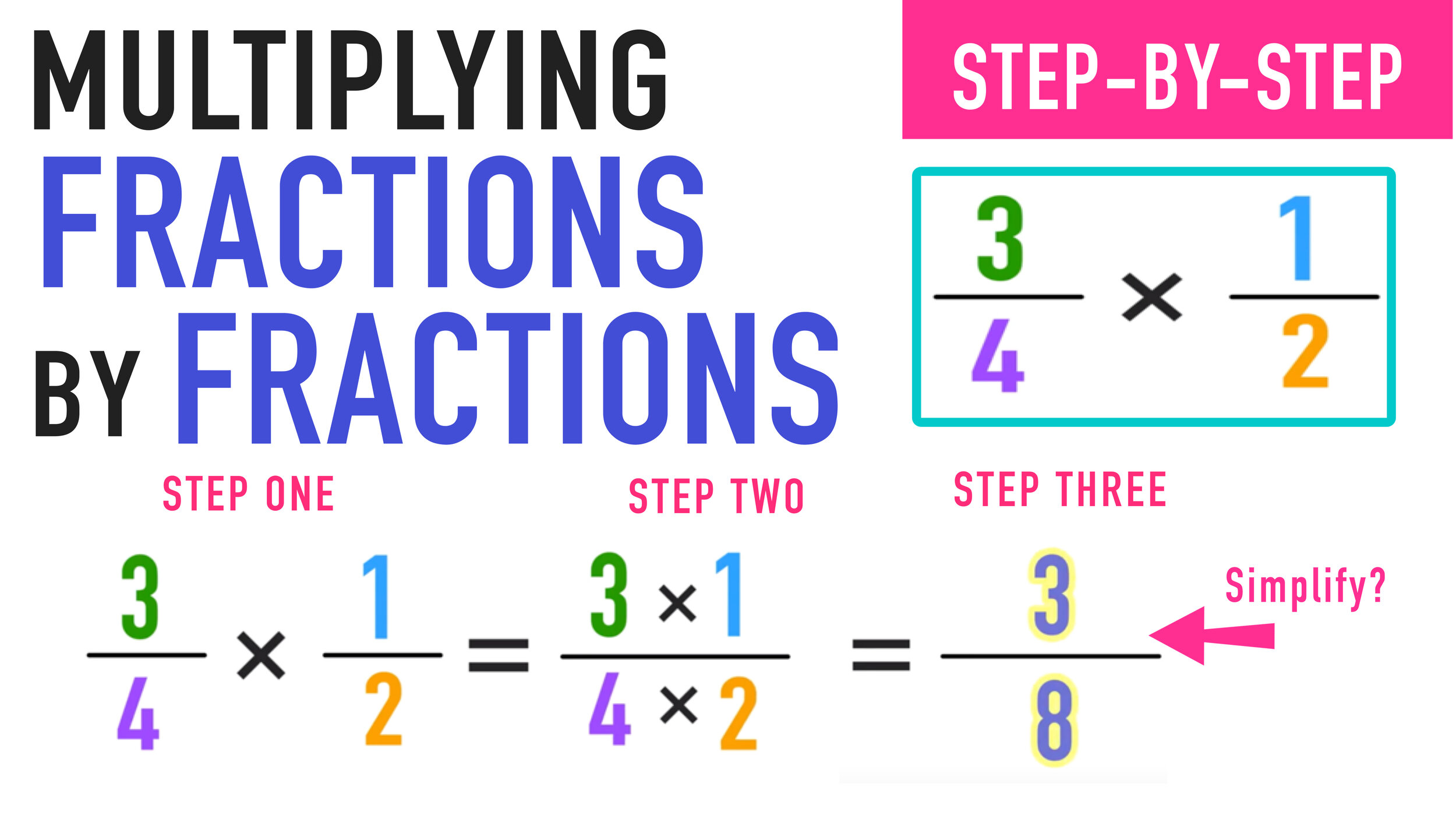
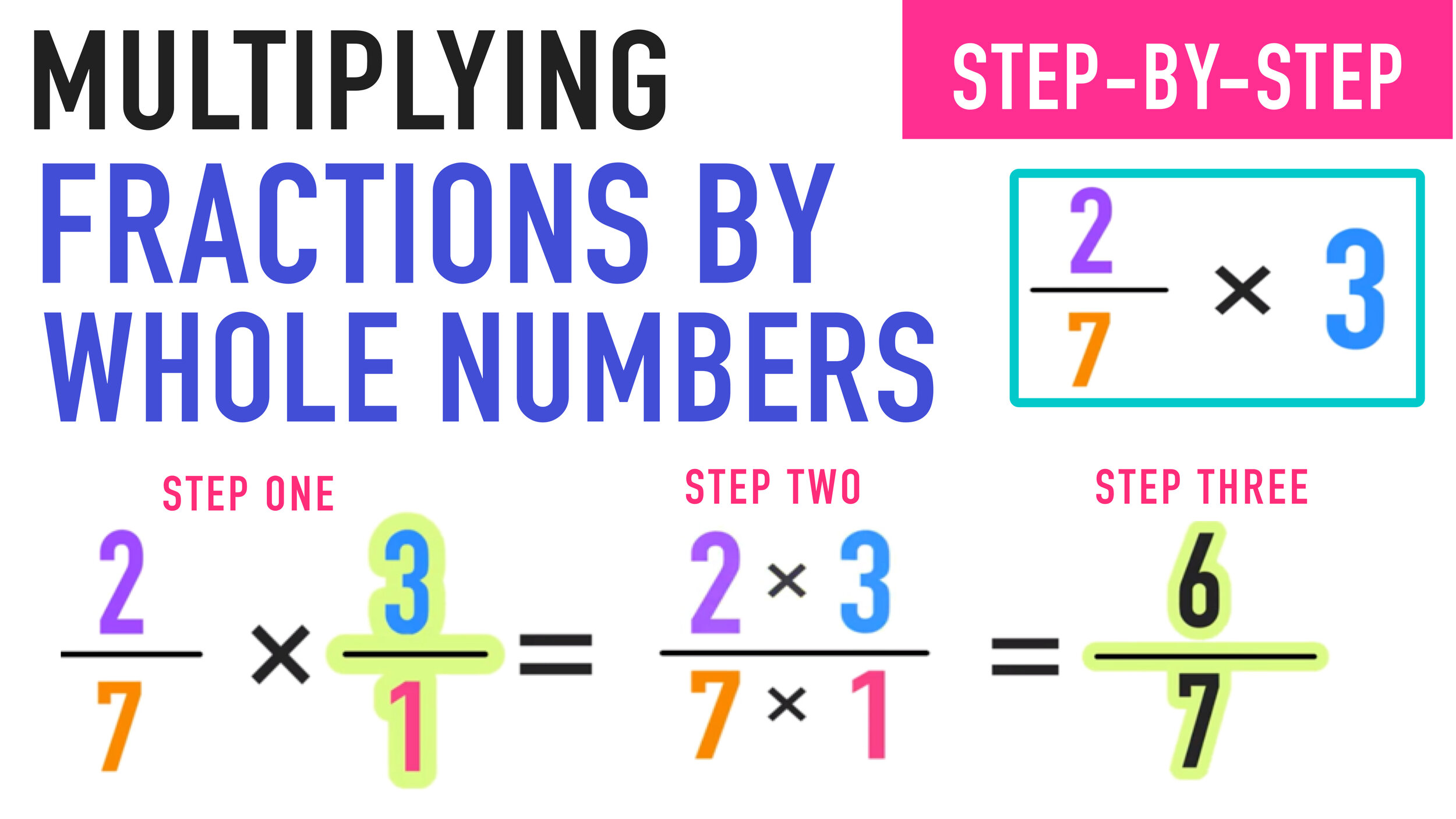
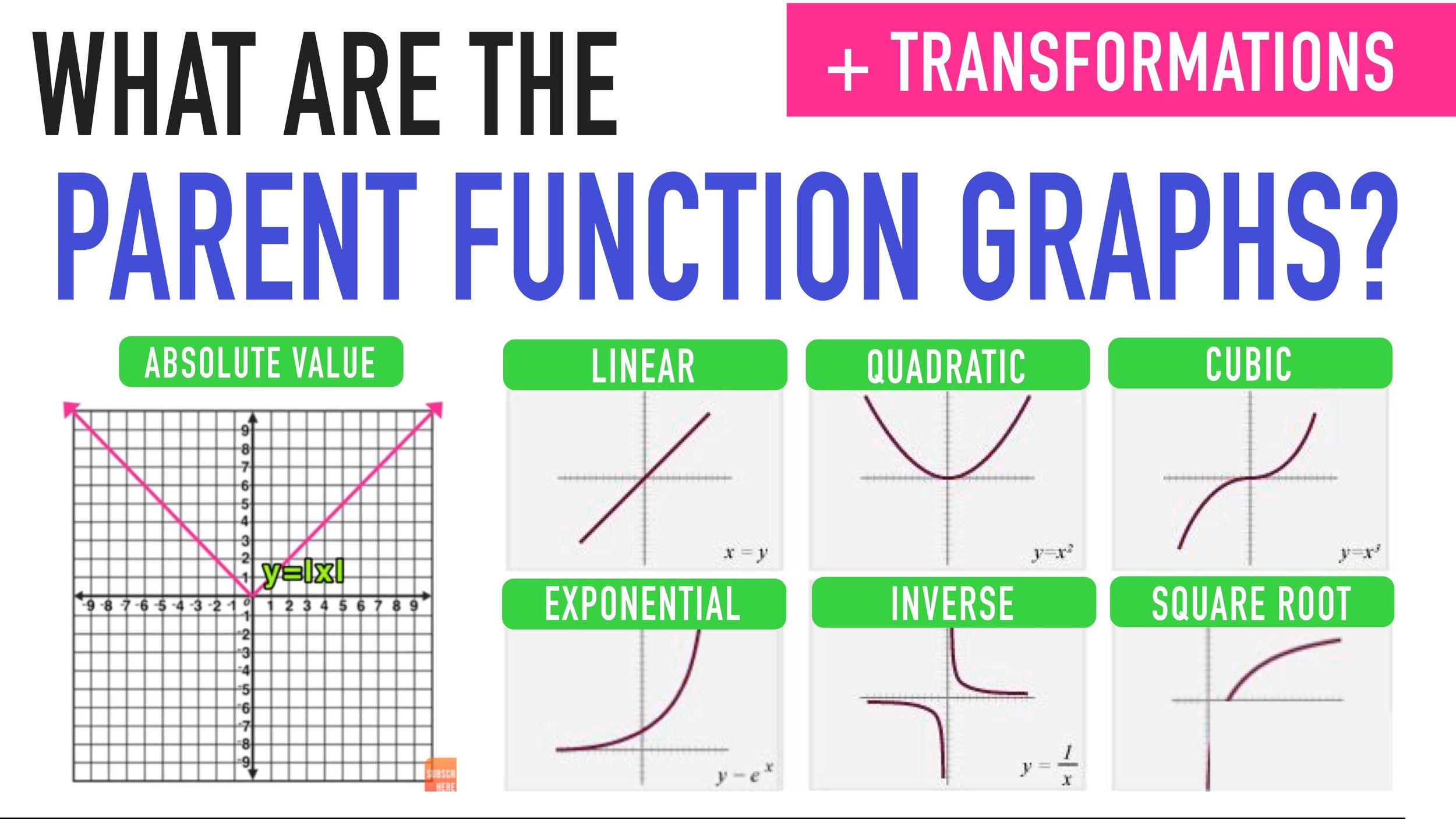
Fraction Chart Uses

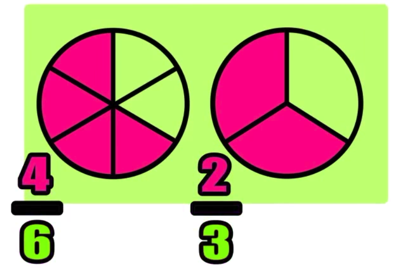
You can use the above fraction chart as a quick reference for comparing fractions and identifying equivalent fractions.

You can also use the chart to help you with adding and subtracting fractions!

We recommend printing out the chart (preferably in color and having it close by whenever you are learning about or working on problems involving fractions.

More Free Fractions Resources and Lessons:

---

Share your ideas, questions, and comments below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Equivalent Fractions Explained—Definitions, Examples, Worksheets

Equivalent Fractions Explained!

What are equivalent fractions in math?

Image Source: Mashup Math FP

Fractions are one of the most important foundational topics in math and students need to understand how to perform operations on fractions like adding and subtracting fractions and multiplying fractions. But, before students can understand fractions at an advanced level, it is critical that they have a strong grasp of equivalent fractions.

In real life, we often deal different values that can be considered equivalent or equal to each other. For example, we know that 60 minutes is equivalent to 1 hour and we also know that 16 ounces are equivalent to one pound. In each case, we are expressing the same amount of time or weight in two different ways that are interchangeable.

This idea of expressing two equal values in different ways is similar in math when it comes to equivalent fractions.

This complete guide to equivalent fractions will provide a step-by-step tutorial on how to understand equivalent fractions and how to find them.

First, let’s start with the equivalent fractions definition:

Math Definition: Equivalent Fractions

Equivalent fractions are fractions that have the same value but do not look the same.

For example, 4/6 and 2/3 are equivalent fractions because they both represent “two thirds.”

Let’s take a look at this example a little closer:

Why are 2/3 and 4/6 equivalent fractions?

Notice that there are three different fractions above: 2/3, 4/6, and 8/12

All three fractions are equivalent fractions. But why?

The reason why they are equivalent fractions is because when you either (A) MULTIPLY or (B) divide both the numerator (top) and denominator (bottom) of each fraction by the same number, the fraction doesn’t change. (If this idea is hard to understand, the images below will help!).

Visual Representation:

---

You can also use a fraction chart as a visual aid to help you to understand and identify equivalent fractions.

⤓ Download Your Free Fraction Chart PDF

---

What about Dividing?

To find equivalent fractions by dividing, take the same steps as multiplying, but mind the following key points:

• Divide both the numerator (top) and denominator (bottom) of each fraction by the same number

• Make sure that whatever number you choose to divide by results in only whole numbers (no decimals)

• Continue dividing until you can not go any further without getting a decimal. At this point, you will have reduced the fraction as much as possible.

Again, you can see that 2/4, 4/6. and 8/12 are equivalent fractions.

How to Test if Two Fractions are Equivalent Using Cross Products:

If you are unsure of whether or not two fractions are equivalent, there is an easy shortcut involving multiplication that you can use as a test.

Rule: Two fractions are equivalent if their cross products are equal.

To find the cross products of two fractions, multiply the top of the first fraction by the bottom of the second fraction AND the bottom of the first fraction by the top of the second fraction.

Equivalent Fractions Example 01: 4/5 and 12/15

To see whether or not 4/5 and 12/15 are equivalent to each other, you have to start by finding the cross products.

Again, multiply the top of the first fraction by the bottom of the second fraction AND the bottom of the first fraction by the top of the second fraction as follows:

4 x 15 = 60

5 x 12 = 60

Notice that both of the cross products equals 60.

Therefore, we can conclude that 4/5 and 12/15 are equivalent fractions because their cross products are the same.

Equivalent Fractions Example 02: 4/7 and 6/12

Just like the last example, you can test to see if the two fractions are equivalent by finding the cross products as follows:

4 x 12 = 48

7 x 6 = 42

Notice that the cross products are not equal: 48 ≠ 42

Therefore, we can conclude that 4/7 and 6/12 are NOT equivalent fractions because their cross products are NOT the same.

---

Conclusion:

• Equivalent fractions are fractions that have the same value but do not look the same or have the same numbers.

• You can create or test equivalent fractions by either multiplying or dividing both the numerator or the denominator by the same number.

• When dividing, you can only work with results that are whole numbers (no decimals!).

• To test whether or not two fractions are equivalent, find the cross products. If the cross products are equal, then the fractions are equivalent.

Need Extra Practice?

Free Worksheet:

⤓ Download Your Free Equivalent Fractions Practice Worksheet and Answer Key

---

Exploring Equivalent Fractions: Video Tutorials

Still confused? Check out the animated video lessons below:

Check out the video lesson below to learn more about equivalent fractions and ratios and for more free practice problems:

---

More Free Fractions Lessons:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Your Kids Will Love These Valentine's Day Math Puzzles

Are you looking for some fun, free, and printable Valentine's Day Math Activities to share with your kids this month?

(We just launched a brand new collection of free Valentine’s Day Math Worksheets for grades K-8! Click here to get your free pdf downloads).

Holiday-themed math puzzles give your kids an opportunity to think critically and deeply about mathematics, develop problem-solving strategies, and work through challenging problems.

And when math problems can channel your students' excitement for Valentine's Day into meaningful learning experiences, engagement will skyrocket!

So, go ahead and try these challenges and puzzles with your kids this month. These free and printable Valentine's Day Math activities are perfect for warm-up and/or cool-down activities and are great for sparking mathematical discussions in your home or classroom. The puzzles are perfect for students in grades 1 through 8.

How to Download: You can download any of the puzzles by right-clicking on the image and saving it to your computer or by dragging-and-dropping it to your desktop.

1.) Find the value of the '?'

Use your math skills to find the value of each icon.

Love = 4

Heart Box = 5

Teddy Bear = 9

Love Birds = 3

? = 7

Hint: 8 minus what value is that same value?

---

2.) Multiplication tables work like a Bingo board, where the value of each box represents the product of its corresponding row and column.

Card = 1

Rose = 2

Heart = 3

Cupid = 6

Chocolates = 18

Looking for more free math challenges like these? click here

---

3.) Which One Doesn't Belong? (simple)

Remember that WODB? activities are meant to spark mathematical thinking and discussion and do not have a single correct answer.

Want to learn more about how to use WOBD? math activities with your kids? click here

---

4.) Multiplication Area Model

Using area model challenge questions is a great strategy for getting kids to think visually about multiplication, which is the approach that Mathematical Mindsets author Jo Boaler recommends most for improving math understanding.

Hint: The area model represents the product of 13 and 9.

Heart = 10

Love Potion = 5

Teddy Bear = 15

Cupid = 12

---

Are you looking for more Valentine’s Day Math Worksheets for students in grades K-8?

Check out our brand new Valentine’s Day Math Worksheet Library to download free holiday-themed pdf worksheets with answer keys.

Click here to get your free pdf worksheets

---

5.) Bonus Geometry Puzzle

Can your kids use their knowledge of area, perimeter, and composite figures to solve this puzzle?

Hint: Two half-circles make one full circle.

Area: approximately 178.5 square cm

Perimeter: approximately 51.4 cm

Do you want to get free math puzzles like this in your inbox every week? Click here to sign up for our free mailing list (includes a free eBook!).

How will you use these math puzzles with your kids? Share your thoughts and suggestions in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math and an advisor to Amazon Education's 'With Math I Can' Campaign. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.

Can You Solve This Famous Math Riddle? (for Ages 10+)

Most People Can’t Figure Out This Simple Math Riddle. Can You?

The Bridge of Destiny Math Riddle is a twist on the famous bridge and torch problem. This math riddle is seemingly simple and a fan favorite for ages 10 and up, yet many people can’t seem to get the correct answer.

If you love math riddles, brain challenges, and epic quests, then give this one a try and see if you have what it takes to find the answer!

Bridge of Destiny Math Riddle:

• Four travelers on a quest must cross a fragile bridge to continue their journey.

•  No individuals can cross the bridge without the Destiny Gem close by, which, fortunately, they have in their possession.

•  If at any time, more than two individuals walk on the bridge, it will collapse.

•  Each traveler moves at a different pace, and it will take each traveler the following amount of time to cross the bridge:

• Sorceress: 1 minute, Archer: 2 minutes, Warrior: 5 minutes, Wizard: 8 minutes

• When two travelers cross the bridge together, they must move at the slower person's pace.

  What is the shortest time needed for all four travelers to safely cross the bridge?

View fullsize

Remember…

•  No more than two individuals can cross the bridge at the same time (otherwise, it will collapse)

•  Individuals must stay together when crossing the bridge and be in possession of the Destiny Gem

•  All four travelers must get safely across

•  No tricks spells, or throwing the Destiny Gem allowed!

---

Ready to Give This Math Riddle a Try?

Chart Example

Go ahead and try and solve the Destiny Bridge Math Riddle on your own before scrolling any further. Come back when you’re ready to see the answer.

(Hint: Using a chart can be very helpful!)

---

Bridge Riddle Answer

View fullsize

Click to enlarge.

Many people conclude that the shortest amount of time for all four travelers to cross the bridge is 17 minutes, but this is incorrect!

***The actual answer is 15 minutes.

To find the correct answer to the riddle, you must realize that having the two slowest individuals cross the bridge individually wastes valuable time which can be saved if they both cross together.

Detailed Explanation:

Check out our animated Destiny Bridge Riddle Video for a detailed explanation of why the answer is 15 minutes AND for a super fun bonus riddle!

---

Ready for a Bonus Riddle?

Wait! Our travelers need your help yet again. Can you solve the bonus riddle?

The River and The Torch

•  Further along their journey, the four travelers must cross a river at night.

•  Crossing the river after dark is only possible with a torch, so the travelers have traded the Destiny Gem for a Torch that will provide light for 17 minutes after it is lit.

•  Only two travelers can cross the river at one time, and they must have the torch in their possession in order to see where they are going.

•  Each traveler takes the following amount of time to cross the river

•  Wizard: 10 Minutes, Sorceress: 5 Minutes, Archer: 2 Minutes, Warrior: 1 Minute

 How can all four travelers cross the river before the torch burns out?

---

Go ahead and try and solve the River and Torch Math Riddle on your own before scrolling any further. Come back when you’re ready to see the answer.

We'll be here waiting for you when you’re done :)

(Hint: Again, using a chart can be very helpful!)

---

View fullsize

River Riddle Answer

***The answer is 17 minutes.

Just like the bridge riddle, to find the correct answer, you have to save time by having the two slowest individuals (in this case, the wizard and the sorceress) cross the bridge together.

Did you get the correct answer?

---

Looking for a pdf worksheet version of the Destiny Bridge riddle?

Click the link below to get your download (answer key included)

Free Destiny Bridge Riddle PDF Worksheet

---

Today’s math riddle is a sample from our best-selling workbook: 101 Math Riddles, Puzzles, and Kids Ages 10+!

Here are some samples from the book:

Guaca-Math

The Gummy Bear Pyramid

In Between

Friday the 13th

101 Math Riddles, Puzzles, and Brain Teasers for Kids Ages 10+! is now available as a PDF download. You can get yours today by clicking here.

Click here to get 100 more math riddles, brain teasers, and puzzles for kids!

---

More Fun Math Riddles and Brain Teasers You Will Love:

Solving Systems of Equations Explained!

This free step-by-step guide will teach you everything you need to know about solving systems of equations in math.

Solving Systems of Equations: Everything You Need to Know

Solving systems of equations can seem intimidating, especially when you see more than one equation shown on a graph. However, if you know how to graph a function on the coordinate plane or on a graphing calculator, then you can become a master of solving systems of equations.

This guide also includes a very handy system of equations solver that you can use to check your work and graph linear systems on your computer.

But first…

If you need some refreshers on the foundational skills required to understand how to solve systems of equations, you may find these free algebra resources to be helpful:

• Intro to Slope and y=mx+b form (video)

• How to graph a line in slope-intercept form (video)

• Quick Guide to Slope: Parallel and Perpendicular Lines

You’ll also notice that the graphics in this lesson rely on using different colors to differentiate between different functions (this strategy is very helpful for keeping your thoughts organized and preventing confusion). If you are following along using graph paper, then it is highly recommended that you use colored highlighters or markers. However, this is only a suggestion, and you can still learn to solve systems of equations using a pen or pencil.

 Are you ready to get started?

System of Equations Definition

A system of equations is when there are two or more equations that share the same variables.

 For example, here is a system of equations for two linear functions:

y = x + 1 & y=-2x + 1

 Notice that both of these equations are shown on the graph in Figure 1. 

(Again, if you need a refresher on how to graph lines in y=mx+b form, watch this quick video tutorial)

Figure 1 (graph courtesy of desmos.com/calculator)

The solution to a system of equations is the point (or points) where the lines intersect.

 So, in this example, the solution to the system of equations is the point (0,1), since this is where the two lines intersect. 

Figure 2: What do lightsaber fights and linear systems have in common? (Image: Mashup Math MJ)

Types of Solutions to Systems of Equations

Does every system of equations have a solution?

There are actually three kinds of solutions to a system of equations:

• One Solution (as seen in Figure 1)

• No Solution

• Infinitely Many Solutions

Figure 3

Key Takeaways:

One Solution: The systems intersect at only one point.

No Solution: The lines are parallel and do (and never will) intersect

Infinitely Many Solutions: Two or more identical and overlapping graphs that intersect everywhere!

Confused? That’s ok. Just keep the three solution types in mind as we work through an example of each type of solution that will help you to better understand how to solve systems of linear equations.

Systems of Linear Equations Examples

Example 01: One Solution

Find the solution to the following system of equations:

The first step to finding the solution to this system of equations is to graph both lines as follows:

Notice that the ONLY intersection point for this system of equations is at (2,5).

Remember that (2,5) is an (x,y) coordinate where x=2 and y=5. To confirm that you answer is correct, you can substitute x=2 and y=5 into both equations to see if your answer checks out as follows.

Note that, since this system of equations has only one solution, (2,5) is the only point that will work. You can try substituting x and y values for any other coordinate and you will never find another one that works out.

Final Answer: The solution is (2,5)

---

Example 02: No Solution

Find the solution to the following system of equations:

Just like the last example, graph both equations on the coordinate plane as follows:

Notice that both equations have the same slope (+5/4). Since parallel lines have the same slope, it makes sense that the lines are the graph are parallel to each other. And, since parallel lines never intersect, these two lines will never intersect, and therefore there is no solution to this system of equations.

Final Answer: No Solution (because the lines are parallel)

---

Example 03: Infinitely Many Solutions

Find the solution to the following system of equations:

Notice that the second equation is not in y=mx+b form, so you will have to rearrange it to isolate the y before you can graph:

Isolate the y by subtracting 3 from both sides.

What do you notice?

Now we have two equations in our system: y=-4x-3 and… y=-4x-3. After rearranging the second equation, we can see that both equations are identical.

What does this mean for the graph and the solution to our linear system? Let’s find out by graphing the first equation (Figure 5) and then the second equation (Figure 6)

Figure 5

Figure 6

Since the equations are identical, the lines are graphed right on top of each other and they intersect everywhere at every point that both lines pass through.

Therefore, every point on the line is a solution—and since lines have an infinite number of points, this system has an infinite number of solutions.

Final Answer: Infinitely Many Solutions

---

Systems of Equations Solver

When you initially learn how to solve systems of equations, we recommend using graph paper and a straight-edge to graph your equations and find your solution (and use substitution to check your work as we did in example 01).

However, after you become more comfortable working with systems of equations, you may benefit from using systems of equations solver tool like a graphing calculator to graph lines and find intersection points rapidly.

If you don’t have a graphing calculator, there is an awesome FREE system of equations solver calculator available via www.desmos.com/calculator.

*Note that you have to input the equations in y= form in order for the Desmos systems of equations solver to work.

For example, you can use the Desmos Systems of Equations Solver to find the solution to the system:

y=(3/5)x-8 & y=(-8/5)x+3

1.) Type each equation into the left-hand column

2.) Locate the intersection point (you may need to zoom out)

3.) Click on the intersection point to find the coordinates.

The solution is (5,-5)

Screenshot of Desmos.com/calculator

---

Systems of Equations Video Lesson

If you are a visual learner and would like to review this step-by-step guide to solving systems of equations as a video tutorial, check out these free tutorials:

---

---

Keep Learning with These Free Math Guides:

---

Share your ideas, questions, and comments below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math . You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.