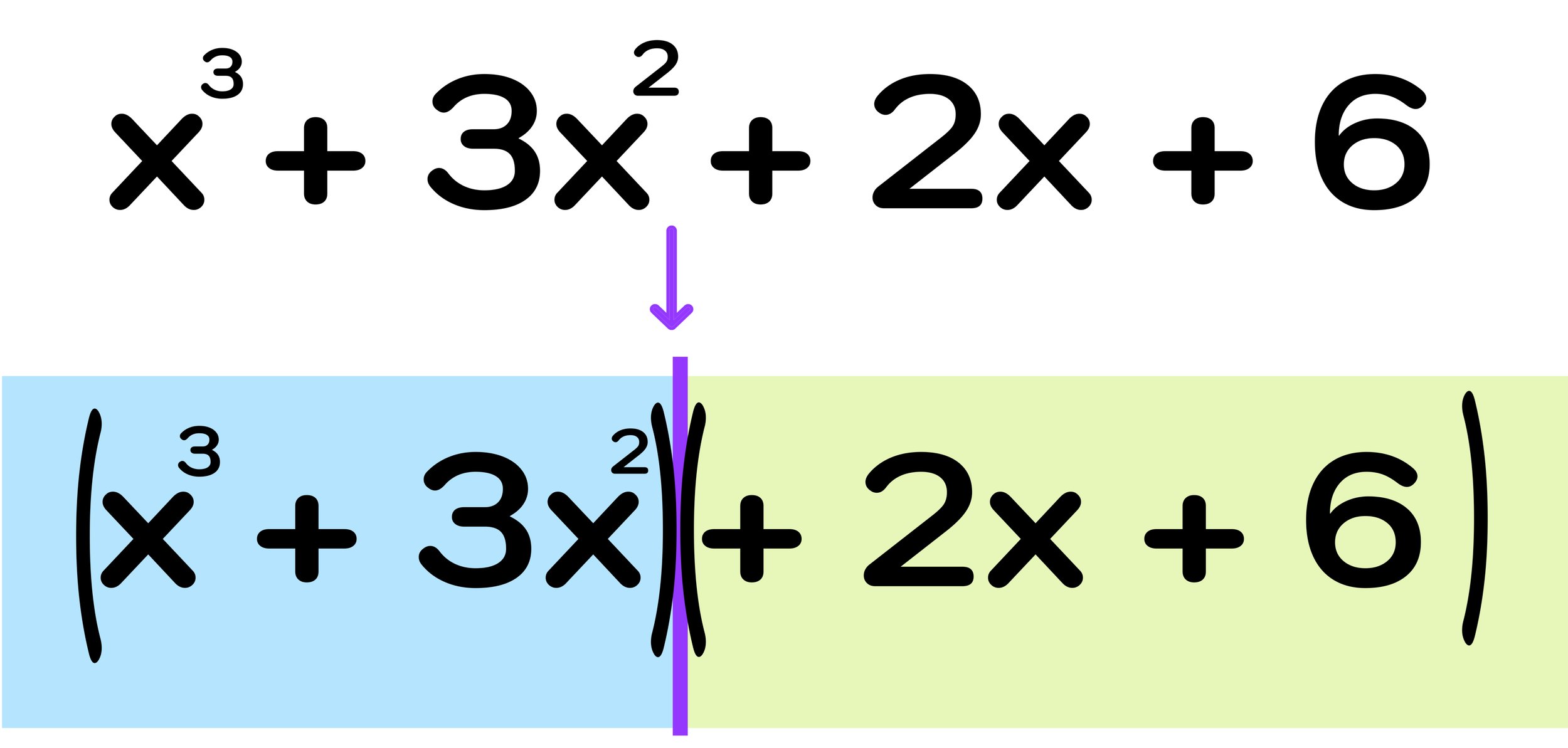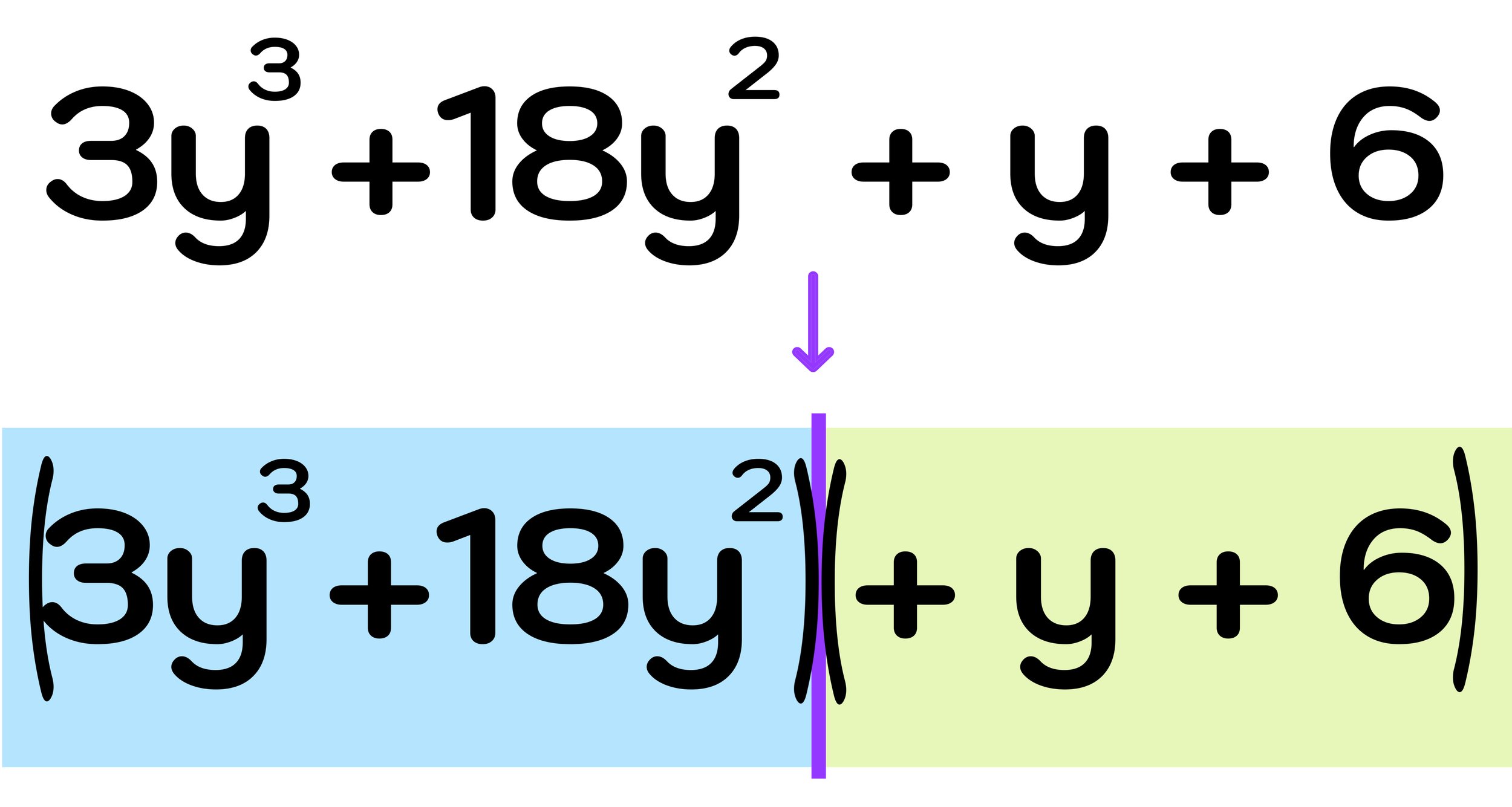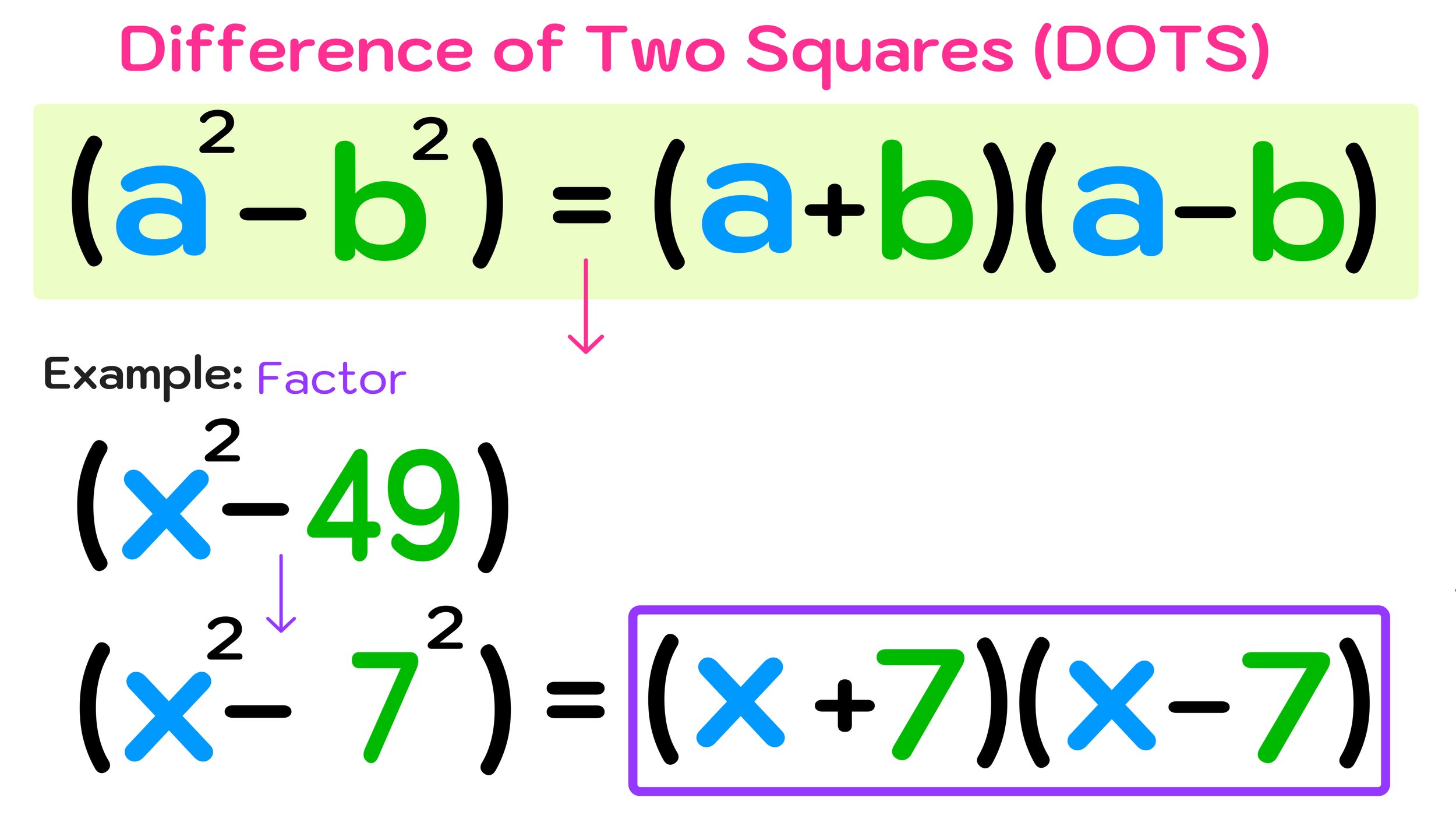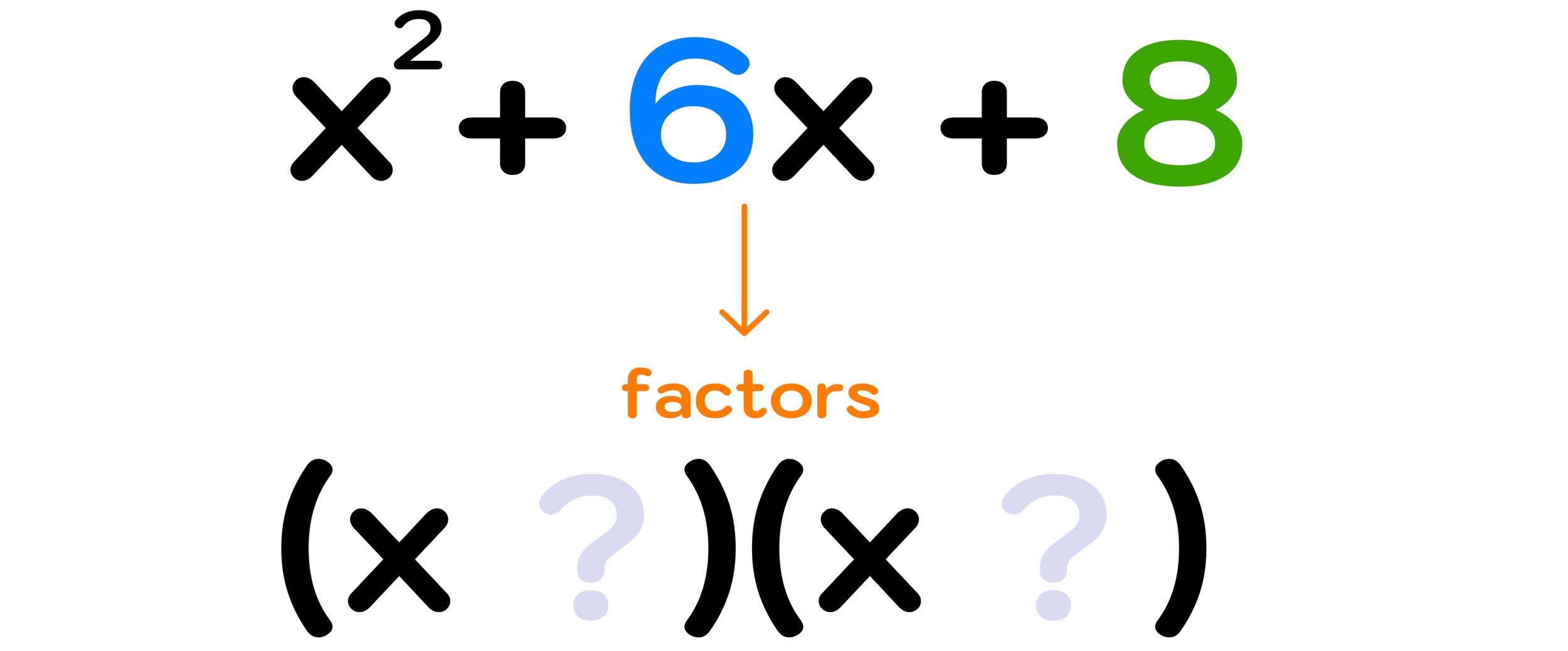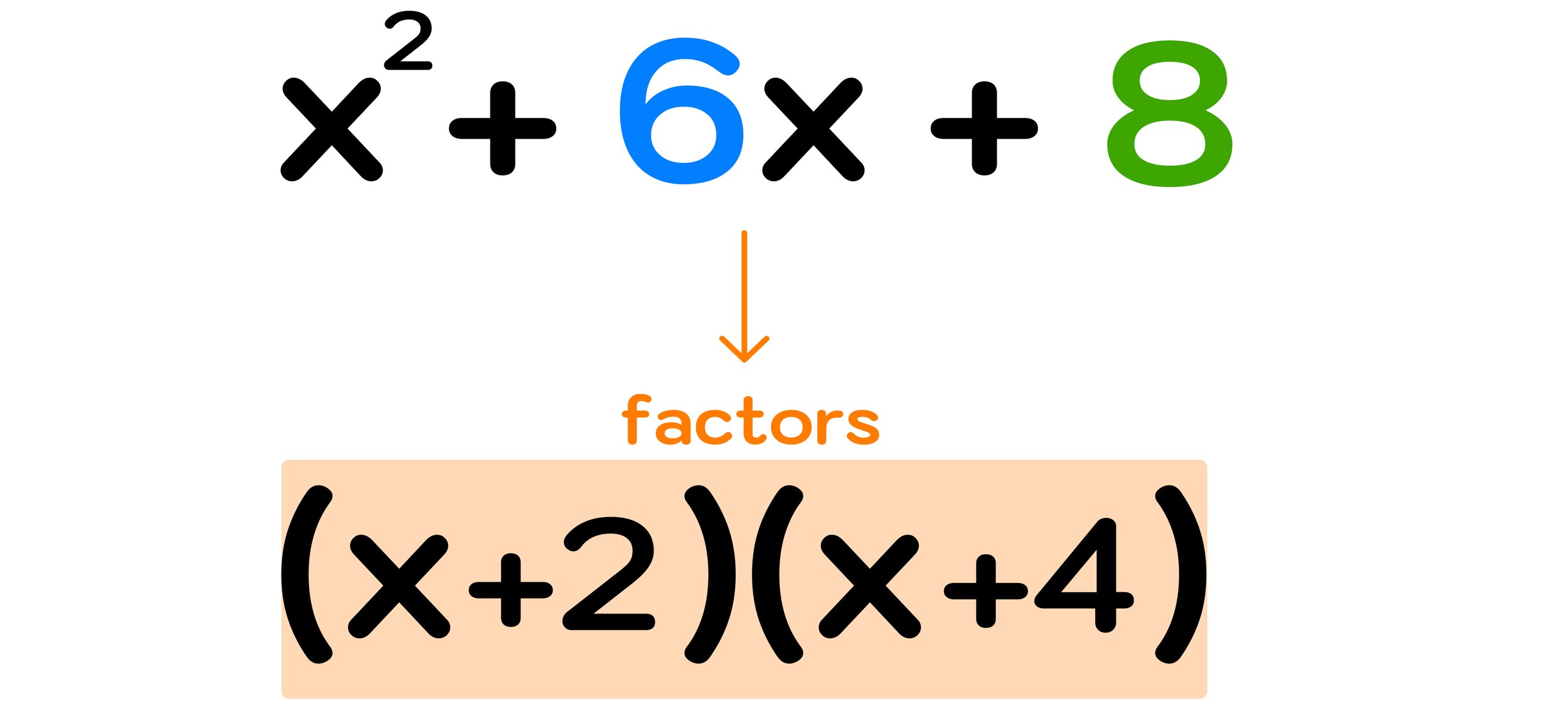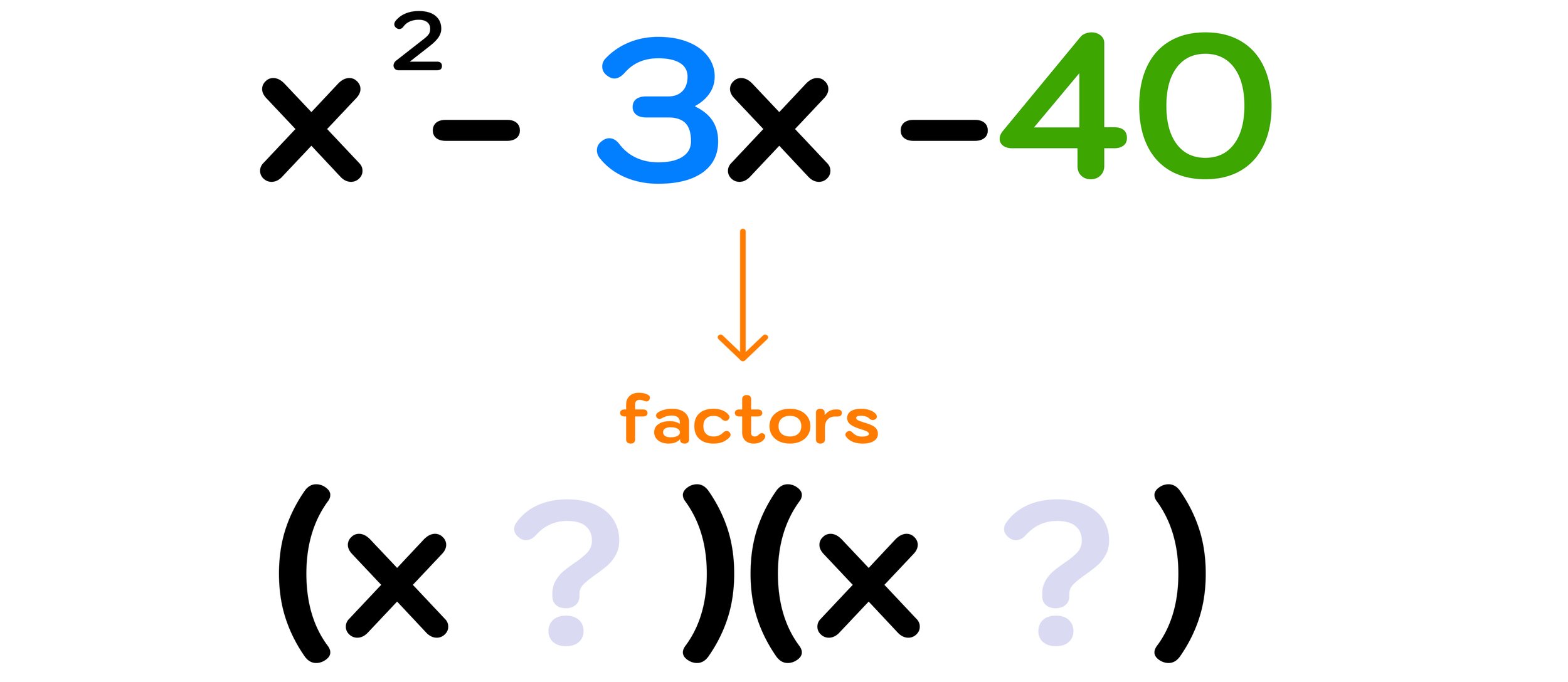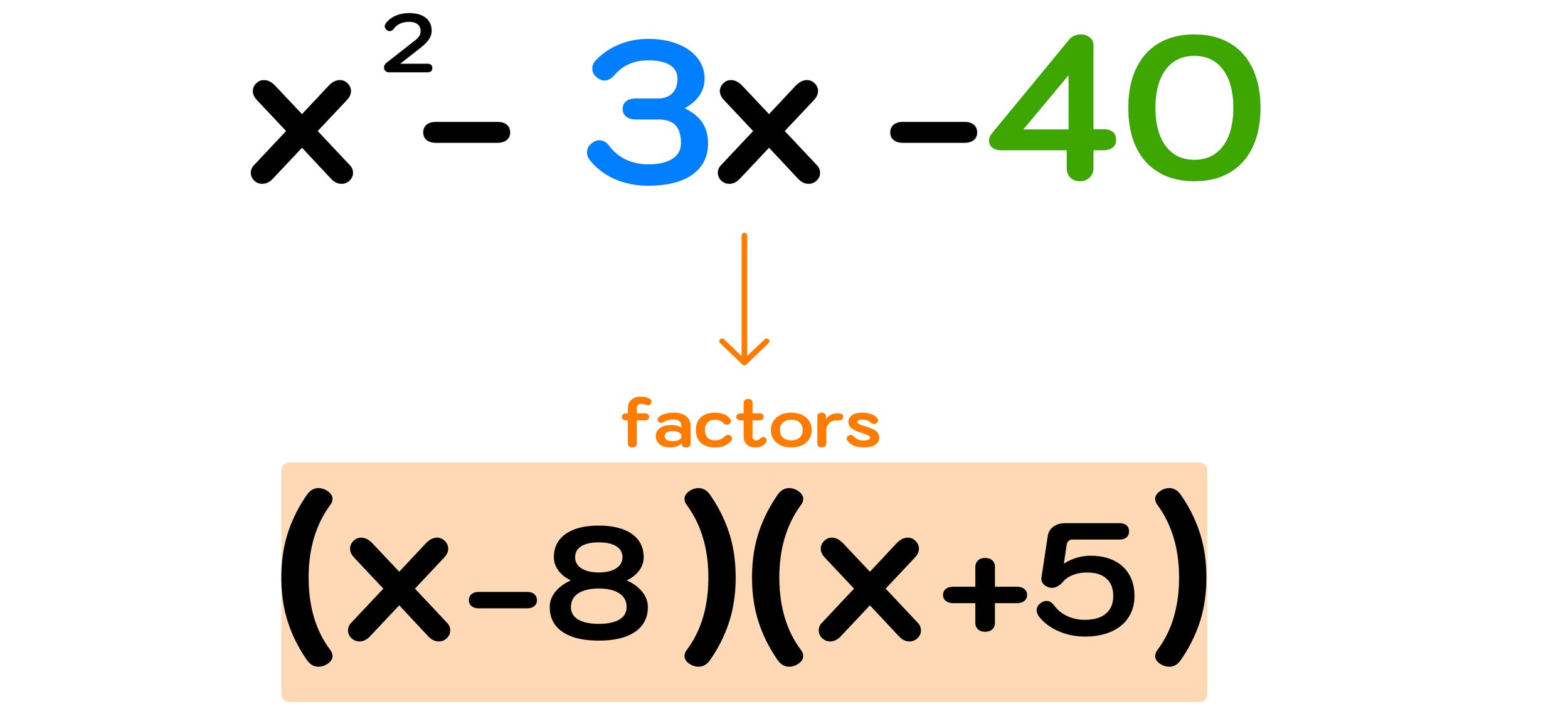Where is the Bermuda Triangle?—Bermuda Triangle Map

Where is the Bermuda Triangle?—Bermuda Triangle Map

Bermuda Triangle Map—Where is the Bermuda Triangle?

Where is the Bermuda Triangle? New Detailed Bermuda Triangle Map Defines its Exact Location Using Google Maps

 

Where is the Bermuda Triangle located on Google Maps? (click to enlarge)

 

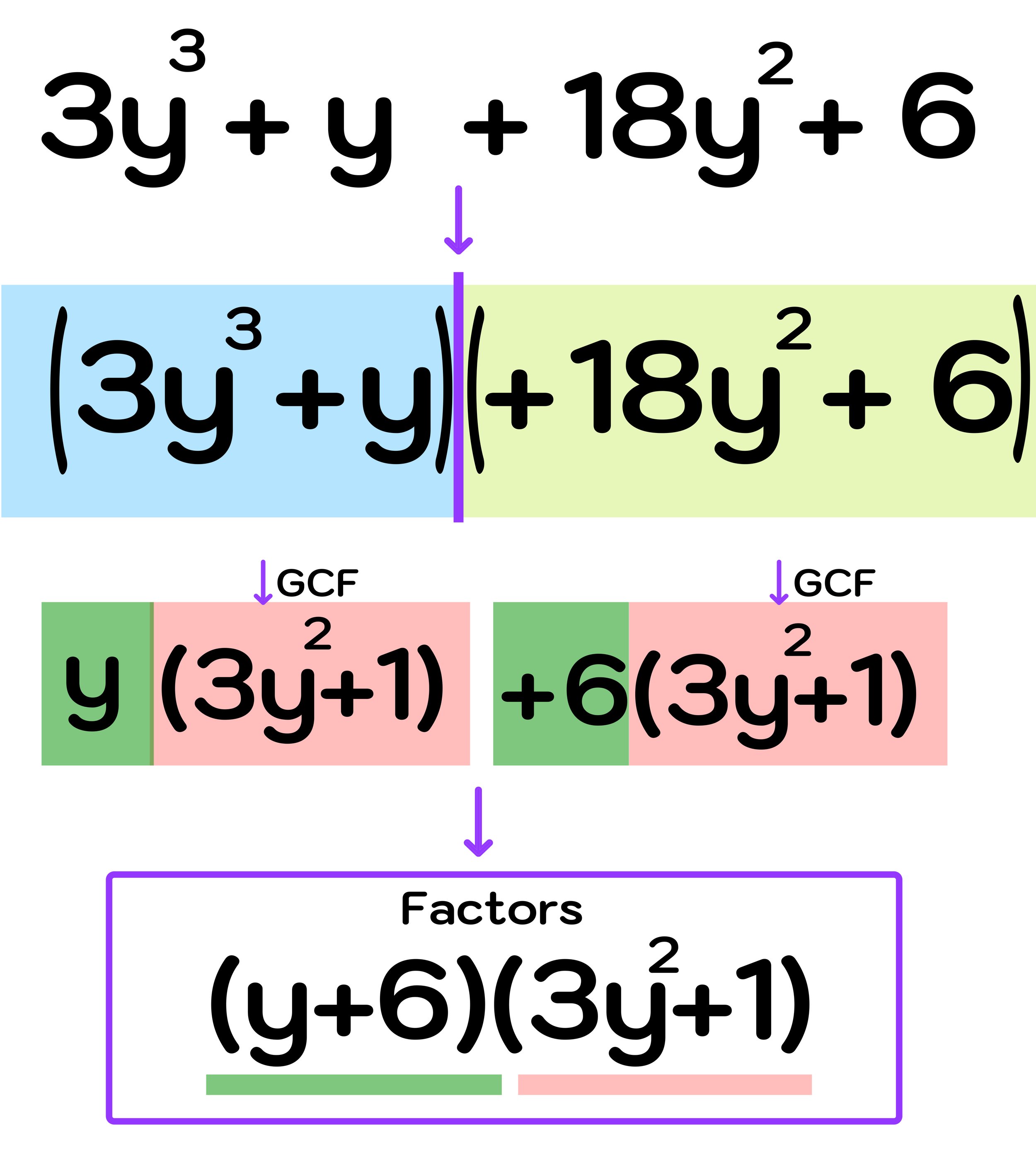
The Bermuda Triangle, also known as the Devil's Triangle, is a geographic region in the western part of the North Atlantic Ocean where many planes and ships have disappeared under mysterious circumstances.

Creating an accurate Bermuda Triangle map can be difficult because there are actually no fixed coordinates for the vertices of the Bermuda Triangle, since the region itself is not an officially recognized area, and its boundaries are not particularly well-defined.

Where is the Bermuda Triangle located on Google Maps? While the Bermuda Triangle is not an officially recognized area, it is possible to display the Bermuda Triangle on a map since its boundaries are generally considered to be between Miami, Bermuda, and Puerto Rico (each location being one of the three points of the triangle)

While the Bermuda Triangle map above (and the alternate version below) is generally considered the most accurate representation of a map of Bermuda Triangle, some sources actually consider the Triangle to extend as far north as Massachusetts and as far south as the Caribbean. However, these sources are in the minority, as the majority of accounts of ships or planes mysteriously going missing are within the boundaries of the Bermuda Triangle contained by Miami, Puerto Rico, and the island of Bermuda.

 

Bermuda Triangle Map: The boundaries of the Bermuda Triangle are generally considered to be between Miami, Bermuda, and Puerto Rico.

 

How Much Area is Occupied by the Bermuda Triangle on a Map?

Since the region that makes up the Bermuda Triangle is not well-defined, its geographic area can only be estimated. Generally speaking, it is said to cover an area of approximately 500,000 to 1.5 million square miles (or about 1.3 to 3.9 million square kilometers) of open ocean.

Despite the many claims of ships and planes mysteriously going missing within this triangular region, the scientific evidence supporting the idea that the Bermuda Triangle is supremely dangerous is lacking. In fact, most evidence suggests that the Triangle is really no more dangerous than any other part of the ocean. But the idea that the Bermuda Triangle is a relatively safe region for sea and air travel has not always been a popular belief, which is why the modern day map of the Bermuda Triangle is a product of several iterations made over the past several decades.

 

If there is no scientific evidence to suggest that the Triangle is dangerous compared to other areas of the ocean, then why have governments and militaries been so interested in accurately showing the Bermuda Triangle on a map?

 

Bermuda Triangle on a Map: History

If you were to search for the Bermuda Triangle on a map today, you would find that it is roughly bounded by Miami, Bermuda, and Puerto Rico. On a map, you can draw three lines connecting these three points to form the “Bermuda Triangle.” Within this triangular region is where the majority of incidents of missing ships and planes have been reported. However, the region known as the Bermuda Triangle is actually not officially recognized by any science, government, or military organization, and there is zero evidence to supporting the idea that the region is supernaturally dangerous.

Still, the Bermuda Triangle continues to be an area of interest and many maps of the region have been created over the years, each containing its own unique features. For example, some maps of the Bermuda Triangle plot the locations of any reported disappearances of ships or planes. Other maps try to highlight potential explanations for the phenomenon, such as atmospheric anomalies and unusual weather patterns.

One of the most famous maps of the Bermuda Triangle was created by Charles Berlitz in his 1974 book The Bermuda Triangle. Like the modern map, Berlitz’ version also has the vertices of the Bermuda Triangle at Puerto Rico, Bermuda, and Miami, Florida. His version includes red dots scatted around the region—each one representing a reported disappearance of a ship or airplane. However, from a modern lens, Berlitz’s map is not entirely accurate and it may include disappearances that are not actually verified or ones that did occur, but not inside of the Bermuda Triangle.

 

The 1974 book The Bermuda Triangle by Charles Berlitz.

 

The U.S. Navy also created a Bermuda Triangle map in 1968. The Navy's depiction of the Bermuda Triangle is a region that is much smaller than typical maps, but with similar boundaries (the Navy also has the vertices of the Triangle being at Bermuda, Puerto Rico, and the southern tip of Florida). Interestingly, the Navy's Bermuda Triangle map includes a note saying that "the area is one of the most heavily traveled shipping lanes in the world, and commercial and pleasure craft routinely navigate through it without incident." This military version of the map stresses that the Bermuda Triangle is not an official region and or an area that is particularly dangerous.

There are also maps of the Bermuda Triangle that present potential explanations for the reported disappearances. One theory is that methane gas hydrates located beneath the ocean floor could be causing ships to sink by reducing the buoyancy of the water. Another theory suggests that unusual weather patterns or ocean currents in the area could be responsible for the incidents.

 

The US Navy began mapping the Bermuda Triangle in 1968.

 

Whether the explanation as to why so many ships and planes have gone missing in the region known as the Bermuda Triangle is scientific or supernatural, the jury is still out. Either way, the region itself will always be a point of interest and fascination for many, which is why establishing the boundaries of the region on a Bermuda Triangle map is so important.

More Free Resources You Will Love:

Free Winning Percentage Calculator—All Sports

Use this free Winning Percentage Calculator to find the WP% of any team or individual athlete in any sport.

Search Tags: where is the bermuda triangle, bermuda triangle map, bermuda triangle on a map, map of bermuda triangle, bermuda triangle on map, map bermuda triangle, map of the bermuda triangle, where is the bermuda triangle located on google maps, bermuda triangle location on map

How to Factorize a Cubic Polynomial

1 Comment

How to Factorize a Cubic Polynomial

How to Factorize a Cubic Polynomial

Step-by-Step Guide: How to Factor a Cubic Polynomial in 3 Easy Steps

 

Free Step-by-Step Guide: How to factor a polynomial with a specific number of terms

 

In algebra, a cubic polynomial is an expression made up of four terms that is of the form:

  • ax³ + bx² + cx + d

Where a, b, c, and d are constants, and x is a variable. Polynomials in this form are called cubic because the highest power of x in the function is 3 (or x cubed).

Unlike factoring trinomials, learning how to factorize a cubic polynomial can be particularly tricky because using any type of guess-and-check method is extremely difficult. However, you can easily learn how to factor a cubic polynomial by using the grouping method described in this guide.

This free Step-by-Step Guide on How to Factorize a Cubic Polynomial will cover the following key topics:

While learning how to factor cubic polynomials can be challenging at first, you can develop your skills pretty quickly just by working through practice problems step-by-step until you become more comfortable with factoring cubic polynomials. So, this guide was designed to teach you everything you need to know about how to factor a cubic polynomial. We recommend that you read through this guide from start to finish and work through each example by following along step-by-step. By the end, you will be able to quickly and accurately factorize a cubic polynomial.

 

Figure 01: How to Factorize a Cubic Polynomial

 

What is a cubic polynomial?

As previously mentioned, a cubic polynomial is a math expression that is of the form ax³ + bx² + cx + d, where a, b, c, and d are all constants and x is a variable, and typically has four terms. Note that x is not the only letter that can be used as a variable in a cubic polynomial. Also, the number in front of any variable is referred to as a coefficient.

Additionally, the terms of a cubic polynomial are the individual “pieces” of the expression, separated by an addition or subtraction sign.

For example, the cubic polynomial in Figure 01 above, x³ + 3x² + 2x + 6 has four terms:

  • 1st Term: x³

  • 2nd Term: 3x²

  • 3rd Term: 2x

  • 4th term: 6

Before you can learn how to factor a cubic polynomial, it is extremely important that you know how to recognize that given polynomial is cubic, so make sure that you deeply understand what a cubic polynomial is before moving forward in this guide.

 

Figure 02: Factoring a Cubic Polynomial

 

What does it mean to factorize a cubic polynomial?

In math, the factors of any polynomial represent components or “building blocks” of the polynomial. Whenever you factor a polynomial (cubic or otherwise), you are finding simpler polynomials whose product equals the original polynomial. Each of these simpler polynomials is considered a factor of the original polynomial.

For example, the binomial x² - 100 has two factors (x + 10) and (x-10).

Why? Lets take a look at what happens when we find the product of the factors by double distributing:

  • (x+10)(x-10) = x² + 10x - 10x - 100 = x² + 0 - 100 = x² - 100

Notice that the result was the original polynomial, x² - 100.

Since cubic polynomials (four terms) are more complex than binomials (two terms), their factors will also be a little more complex, but the idea is still the same—factoring a cubic polynomial involves finding simpler polynomials or “building blocks” whose product is the original cubic polynomial.

And, to factorize a cubic polynomial, we will be using a strategy called grouping that will allow you to factor any cubic polynomial (assuming that it is factorable at all) using 3 easy steps. So, lets go ahead and work three practice problems to give you some experience with factoring cubic polynomials by grouping.

Now that you understand the key terms and the difference between a polynomial with 2 terms, 3 terms, and 4 terms.

For factoring each type of polynomial, we will look at two methods: GCF, direct factoring, and, sometimes, a combination of the two.

Let’s get started!

How to a Factorize a Cubic Polynomial Examples

Now, you will learn how to use the follow three steps to factor a cubic polynomial by grouping:

Step One: Split the cubic polynomial into two groups of binomials.

Step Two: Factor each binomial by pulling out a GCF

Step Three: Identify the factors

As long as you follow these three steps, you can easily factor a given polynomial, though note that not all cubic polynomials are factorable."

We will start by factoring the cubic polynomial shown in Figure 01: x³ + 3x² + 2x + 6

Example #1: Factor x³ + 3x² + 2x + 6

 

Figure 03: We have to find the factors of x³ + 3x² + 2x + 6

 

To factorize this cubic polynomial, we will be applying the previously mentioned 3-step method as follows:

Step One: Split the cubic polynomial into groups of two binomials.

To factor this cubic polynomial, we will be using the grouping method, where the first step is to split the cubic polynomial in half into two groups.

 

Figure 04: The first step to factoring a cubic polynomial is to split it into groups of two binomials.

 

For Example #1, at the end of the first step, you have split the cubic binomial down the middle to form two groups of binomials:

  • (x³ + 3x²)

  • (2x + 6)

Why are you splitting the cubic polynomial like this? Notice that it is not possible to pull a Greatest Common Factor (GCF) out of the original cubic polynomial x³ + 3x² + 2x + 6. The goal of the first step is to create two separate binomials, each with a GCF that can be “pulled out.”

 

Figure 05: Make sure that each individual binomial has a GCF before moving onto the next step.

 

Step Two: Factor each binomial by pulling out a GCF

Again, the purpose of the first step is to split the cubic polynomial into two binomials, each with a GCF. Before moving forward, ensure that each individual binomial has a GCF; otherwise, you may need to swap the positions of the middle terms (3x² and 2x). Swapping these middle terms is not required for this first example; however, we will work through an example later on where this is required.

Now, for step two, you can divide the GCF out of each grouping as follows:

  • (x³ + 3x²)→ x²(x +3)

  • (2x + 6) → 2(x + 3)

This process of pulling the GCF out of each binomial is illustrated in Figure 05 below.

 

Figure 06: To factorize a cubic function, split it into two groups and then pull a GCF out of each group.

 

Step Three: Identify the factors

After completing the second step, you are left with:

  • x²(x +3) + 2(x+3)

Notice that both groups share a common term, which, in this case, is (x+3). This result is expected and is a signal that you are factoring the cubic polynomial correctly. If the groups do not share a common terms, then it is likely that the cubic polynomial is not factorable or that you made a mistake pulling out the GCF.

However, since you factored each group and ended up with a common factor of (x+3), you can move on to determining the factors of the cubic polynomial.

The illustration in Figure 06 above color-codes how you use the results from step two to determine the factors of the cubic polynomial.

You already know that one of the factors is (x+3). To find the other factor, you can simply take the two “outside” terms, in this case, x² and +2.

  • x²(x +3) + 2(x+3) → (x²+2)(x+3)

Final Answer: The factors of x³ + 3x² + 2x + 6 are (x²+2) and (x+3)

The entire 3-step method that we just used to factor a cubic polynomial by grouping is shown in Figure 07 below:

 

Figure 07: How to factorize a cubic polynomials step-by-step

 

How can you check if your factors are actually correct? You can perform double distribution to multiply the binomials together to see if the result is indeed the cubic polynomial that you started with. If it is, then you know that you have factorized correctly.

You can see in Figure 08 below that multiplying the factors together does indeed result in the original cubic polynomial, so you know that your factors are correct:

  • (x²+2)(x+3) = x³ + 3x² + 2x + 6

 

Figure 08: Check your answer using double distribution

 

Now, lets go ahead and work through another example of how to factor a cubic polynomial.

Example #2: Factor 2x³ - 3x² + 18x - 27

Just like in the first example problem, you can use the 3-steps for factoring a cubic polynomial by grouping as follows:

 

Figure 09: Find the factors of the cubic polynomial 2x³ - 3x² + 18x - 27

 


Step One: Split the cubic polynomial into groups of two binomials.

After splitting this cubic polynomial, you end up with these two groups: (2x³ - 3x²) and (18x-27)

 

Figure 10: Step One: Split the cubic polynomial into two groups

 

Step Two: Factor each binomial by pulling out a GCF

Next, divide a GCF out of each group (if possible) as follows:

  • (2x³ - 3x²) → x²(2x - 3)

  • (18x - 27) → 9(2x - 3)

This process of pulling a GCF out of each group is illustrated in Figure 11 below:

 

Figure 11: Factorize a cubic polynomial

 

Step Three: Identify the factors

Since both factors have a common term, (2x-3), you know that you have likely factored correctly and you can move onto identifying the factors.

Final Answer: (x²+9) and (2x-3) are the factors of the cubic polynomial 2x³ - 3x² + 18x - 27.

All of the steps for solving Example #2 are illustrated in Figure 12 below.

 

Figure 12: The factors are (x²+9) and (2x-3)

 

Just like the last example, you can check to see if your final answer is correct by multiplying the factors together and seeing if the result equals the original cubic polynomial.

Example #3: Factor 3y³ + 18y² + y + 6

Finally, lets work through one more example where you have to factorize a cubic polynomial.

Step One: Split the cubic polynomial into groups of two binomials.

Again, the first step is to split the cubic polynomial down the middle into two binomials as shown in Figure 13 below.

 

Figure 13: Factoring a cubic polynomial by grouping.

 

As shown in Figure 13 above, splitting the polynomial down the middle leaves you with these two groups: (3y³ +18y²) and (y+6)

Remember that the whole point of splitting the cubic polynomial is to create two binomials that each have a GCF. But notice that the second binomial, (y+6), is not factorable because there is no GCF between +y and +6.

But, as previously mentioned, this doesn’t mean that you can not solve this problem further. In fact, the commutative property of addition allows you to swap the positions of the two middle terms (18y² and +y).

This extra step of swapping the two middle terms is illustrated in Figure 14 below.

 

Figure 14: Sometimes you have to swap the positions of the middle terms in order to factorize a cubic polynomial.

 

After swapping the positions of the middle terms, you can now apply the 3-step method to factoring the equivalent polynomial: 3y³ + y + 18y² + 6 (this new cubic polynomial is equivalent to the original because the commutative property of addition allows you to rearrange the terms without changing the value of the expression).

Now, you actually can split the new cubic polynomial into groups that can be factoring by dividing out a GCF: (3y³ + y) and (18y² + 6)

 

Figure 15: After swapping the positions of the middle terms, you can continue on with factoring the cubic polynomial.

 

Step Two: Factor each binomial by pulling out a GCF

As shown in Figure 15 above, you can factor each group by pulling out a GCF as follows:

  • (3y³ + y) → y(3y² + 1)

  • (18y² + 6) → 6(3y² + 1)

Step Three: Identify the factors

Finally, you can conclude that:

Final Answer: The factors are (y+6) and (3y² + 1)

The step-by-step process to solving this 3rd example are shown in Figure 16 below. Again, you can make sure that your final answer is correct by multiplying the factors together and verifying that their product is equivalent to the original cubic polynomial.

 

Figure 16: How to factorize a cubic polynomial when you have to swap the middle terms.

 

How to Factorize a Cubic Polynomial: Conclusion

It is beneficial to understand how to factorize a cubic polynomial because the skill will allow you to simplify and understand the behavior of cubic functions as you continue onto higher levels of algebra and begin to explore topics like finding roots, analyzing graphs, and solving cubic equations.

Factoring cubic functions can be challenging, but you can always use the following 3-step grouping method described in this guide to successfully factor a cubic polynomial (assuming that it is factorable in the first place):

Step One: Split the cubic polynomial into groups of two binomials.

Step Two: Factor each binomial by pulling out a GCF

Step Three: Identify the factors

Keep Learning:

1 Comment

How to Factor Polynomials—Step-by-Step Examples and Tutorial

How to Factor Polynomials—Step-by-Step Examples and Tutorial

How to Factor Polynomials Explained

Step-by-Step Guide: How to Factor Polynomials with 2 Terms, How to Factor Polynomials with 3 Terms, How to Factor Cubic Polynomials

 

Free Step-by-Step Guide: How to factor a polynomial with a specific number of terms

 

In algebra, a polynomial is an expression made up of variables and coefficients separated by the operations of addition and/or subtraction.

Polynomials are a fundamental math topic and understanding how to work with them (including factoring) is essential to being successful in algebra and beyond. Learning how to factor polynomials with 2, 3, or 4 terms involves understanding how to break down a given polynomial into simpler factors.

This free Step-by-Step Guide on How to Factor Polynomials will cover the following topics:

While learning how to factor polynomials can be challenging, it is a learnable skill that can be acquired through practice. The goal of this free guide on how to factor polynomials is to give you plenty of step-by-step practice with factoring polynomials—including polynomials with 4 terms (cubic polynomials)—so that can become more comfortable with factoring all kinds of polynomials.

Before we cover everything you need to know about how to factor a polynomial, let’s quickly recap some key algebra vocabulary terms and phrases that you will need to be familiar with in order to use this guide.

 

Figure 01: How to Factor Polynomials: What is a Polynomial?

 

What is a polynomial?

As previously stated, a polynomial is a math expression comprised of variables, coefficients, and/or constants separated by the operations of addition or subtraction.

The terms of polynomials are individual parts, or monomials, separated by addition or subtraction signs.

For example,

  • 3x² is a monomial

  • 3x² + 6x is a polynomial with 2 terms (3x² and 6x)

  • 3x² + 6x - 15 is a polynomial with 3 terms (3x², 6x, and -15)

  • 9x³ + 3x² + 6x - 15 is a polynomial with 4 terms (9x³, 3x², 6x, and -15)

Figure 01 above illustrates the difference between a monomial and a polynomial.

For an expression to be considered a polynomial, it must have at least two terms, but there is no limit on how many terms a polynomial can have.

When it comes to factoring polynomials, you will most commonly be dealing with polynomials that have 2 terms, 3 terms, or 4 terms:

  • A polynomial with 2 terms is called a binomial

  • A polynomial with 3 terms is called a trinomial

  • A polynomial with 4 terms is called a quadrinomial (also known as a cubic polynomial)

Examples of a polynomial with 2 terms, 3 terms, and 4 terms are shown in Figure 02 below.

 

Figure 02: How to factor polynomials with 4 terms or less.

 

Now that you understand the key terms and the difference between a polynomial with 2 terms, 3 terms, and 4 terms.

For factoring each type of polynomial, we will look at two methods: GCF, direct factoring, and a combination of the two.

Let’s get started!

How to Factor Polynomials with 2 Terms

We will start by learning how to factor polynomials with 2 terms (binomials).

Whenever you are factoring a polynomial with any number of terms, it is always best to start by looking to see if there is a GCF—or greatest common factor—that all of the terms have in common.

For example, consider the following example:

Example #1: Factor 8x + 4

For this example, you should notice that both terms, 8x and 4 are divisible by 4, hence they share a GCF of 4.

Therefore, you can divide out the GCF of 4 from both terms as follows:

  • 8x + 4 → 4 (2x + 1)

So, the factors of 8x + 4 are: 4 and (2x+1).

What we just did was essentially the reverse of the distributive property, as shown in Figure 03 below.

 

Figure 03: How to factor a polynomial with 2 terms using the GCF method.

 

Note that many binomials can be factored using the GCF method, so let’s gain a little more practice with one more example (understanding how to simplify and/or factor a polynomial using the GCF method will come in handy when you start factoring 3 and 4 term polynomials later on).

Example #2: Factor 6x² + 12x

Just like the first example, there is a GCF for both terms. But, in this case, the GCF includes a variable. Why? Because both terms have coefficients that are divisible by 6 and both terms have at least one x variable, so the GCF, in this case, is 6x.

Therefore, you can divide out 6x from both terms as follows:

  • 6x² + 12x → 6x(x + 2)

So, the factors of 6x² + 12x are: 6x and (x+2).

Again, this method of factoring is just the reverse of the distributive property and is illustrated in Figure 04 below.

 

Figure 04: How to factor a polynomial with 2 terms using the GCF method.

 

Next, we will look at a special case of factoring a binomial—when the binomial is a difference of two squares (this is sometimes referred to as DOTS).

Whenever you have a binomial of the form a²-b², the factors will be of the form (a+b)(a-b).

Example #3: Factor x² - 49

For example, if you wanted to factor the binomial: x² - 49, you would notice that both x² and 49 are squares:

  • x² = (x)(x)

  • 49=(7)(7)

So, another way to write (x²- 49) is (x²- 7²)

Therefore, you can use the DOTS method for factoring binomials. In this case, a = x and b = 7, so:

  • (a²-b²) = (a+b)(a-b) → (x²- 7²) = (x-7)(x+7)

You can now conclude that the factors of x²- 49 are (x-7) and (x+7) using the DOTS method.

This process is illustrated in Figure 05 below:

 

Figure 05: How to factor a polynomial that is the difference of two squares.

 

If you want to learn more about the DOTS method for factoring polynomials that are the difference of two squares, check out this free video tutorial on YouTube for more practice.

Otherwise, let’s continue onto the next section where you will learn how to factor polynomials with 3 terms.

How to Factor Polynomials with 3 Terms

Moving on, we will now look at polynomials with 3 terms, typically referred to as trinomials

Learning how to factor polynomials with 3 terms involves a more involved factoring process that we will explore in this section.

The trinomials that we will cover will be of the form ax² + bx + c (where c is a constant). The strategies that we will use will depend on whether a (the leading coefficient) equals one or not. Therefore, the first two examples in this section will be factoring trinomials when a=1 and the second two examples will be when a≠1.

How to Factor Polynomials with 3 Terms when a=1

Example #1: Factor x² + 6x + 8

For the first example, we have to factor the trinomial: x² + 6x + 8

 

Figure 06: How to factor polynomials with 3 terms (when a=1)

 

Again, the leading coefficient, a, is equal to 1 in this example. This is important to note because the following method for factoring a trinomial only works when a=1.

Now we are ready to factor this trinomial in 3 easy steps:

Step One: Identify the values of b and c.

In this example, the values of b and c in the trinomial are: b=6 and c=8

Step Two: Figure out two numbers that both ADD to b and MULTIPLY to c.

The second step often involves some of trial-and-error as you pick numbers and see if they meet both conditions (the two numbers have to add together to make b and multiply together to make c).

  • 5 + 1 =6 (the value of b) ✓

  • 5 x 1 ≠ 8 (the value of c) ✘

For example, lets say that you chose the numbers 5 and 1. While 5+1=6 is true (satisfying the first condition), 5x1=5 (not 8), therefore, they do not satisfy the second condition. So, 5 and 1 do not work.

But, if you picked the numbers 2 and 4, you can see that:

  • 2 + 4 =6 (the value of b) ✓

  • 2 x 4 = 8 (the value of c) ✓

Since 2 and 4 satisfy both conditions, you can stop searching and move onto the third step.

Step Three: Use your numbers from step two to write out the factors

In this case, you can conclude that the factors of x² + 6x + 8 are (x+2) and (x+4).

 

Figure 07: The factors of x² + 6x + 8 are (x+2) and (x+4).

 

You can verify that these are the correct factors by performing double distribution as follows:

  • (x+2)(x+4) = x² + 2x + 4x + 7 = x² + 6x + 8

Notice that you ended up with the trinomial that you started with! Now, lets work through one more example of how to factor polynomials with 3 terms when a=1.

Example #2: Factor x² - 3x - 40

For this next example, we have to factor the trinomial: x² - 3x - 40

 

Figure 08: How to factor 3rd degree polynomials

 

Notice that, in this case, the trinomial includes subtraction signs, which will affect how you perform step two below.

Step One: Identify the values of b and c.

For this trinomial, b= -3 and c= -40

Step Two: Figure out two numbers that both ADD to b and MULTIPLY to c.

Again, you have to find two numbers that add to make -3 and that multiply together to make -40.

This part can be tricky when both of the values for b and c are negative (like in this example). You have to recall that a negative number times another negative number will lead to a positive result, so you can’t have two negatives (since you need to find two numbers that multiply together to make -40).

Eventually, after some trial-and-error, you should find that -8 and +5 satisfy both conditions:

  • -8 + 5 =-3 (the value of b) ✓

  • -8 x 5 = -40 (the value of c) ✓

Step Three: Use your numbers from step two to write out the factors

Finally, you can conclude that the factors of x² - 3x -40 are (x-8) and (x+5).

(You make sure that this answer is correct, you can perform double distribution on (x-8)(x+5) to make sure that the result is equal to the original trinomial).

 

Figure 09: The factors of x² - 3x -40 are (x-8) and (x+5).

 

If you want more practice factoring trinomials when a=1, check out our free step-by-step guide on how to factor trinomials to gain some more practice.

Otherwise, you can continue on to learn how to factor polynomials with 3 terms when a≠1.

How to Factor Polynomials with 3 Terms when a≠1

Example #1: Factor 2x² - x - 6

For the first example, we have to factor the trinomial: 2x² - x - 6

 

Figure 10: How to factor polynomials with 3 terms when a≠1

 

For starters, notice that you can not pull out a GCF.

So, to solve trinomials of the form ax² + bx + c when a≠1, you can use the AC method as follows:

Step One: Identify the values of a and c and multiply them together

In this case, a=2 and c=-6, so

  • a x c = 2 x -6 = -12

Step Two: Factor and replace the middle term

The second step requires you to use the result from step one to factor and replace the middle term.

The middle term is currently -1x and note that:

  • -12 = -4 x 3; and

  • -4 + 3 = -1

We chose -4 and 3 as factors because the sum of -4 and 3 equals negative 1, so we can rewrite the original trinomial as 2x² - 4x +3x - 6

 

Figure 11: Factor and replace the middle term

 

Step Three: Split the new polynomial down the middle and take the GCF of each side

Note that we are now working with a polynomial that actually has four terms: 2x² - 4x + 3x - 6

In this third step, you have to split the polynomial down the middle to essentially create two separate binomials that you can simplify by dividing GCF’s out of as follows:

  • First Half: 2x² - 4x = 2x(x-2)

  • Second Half: 3x - 6 = 3(x-2)

This third step is illustrated in Figure 12 below:

 

Figure 12: Split the new polynomial down the middle and take the GCF of each side

 

Step Four: Identify the Factors

Finally, you are ready to identify the factors.

The result from the previous step was 2x(x - 2) + 3(x -2). Hidden within this expression are your two factors, which you can see by looking at Figure 13 below.

 

Figure 13: The final step is to identify the factors

 

Finally, you can conclude that the factors of 2x² - x - 6 are (2x+3) and (x-2).

Clearly, factoring a trinomial when a≠1 can be a tricky and there are several steps along the way, but, the more that you practice this process, the better you will become at factoring polynomials with 3 terms like the one in this past example. To give you a little more practice, lets work through one more example before we move on to learning how to factor cubic polynomials.

Example #2: Factor 4x² - 15x + 9

 

Figure 14: Factor the trinomial where a=4, b=-15, and c=9

 

Step One: Identify the values of a and c and multiply them together

In this example, a=4 and c=9, so

  • a x c = 4 x 9 = 36

Step Two: Factor and replace the middle term

For the next step, note that the middle term is -15x, so you will need to find two numbers that multiply to 36 and add to -15:

  • 36 = -12 x -3; and

  • -12 + -3 = -15

Now, we can rewrite the original trinomial as 4x² -12x -3x +9

Step Three: Split the new polynomial down the middle and take the GCF of each side

For step three, you have to split the polynomial into two separate binomials and divide a GCF out of each one as follows:

  • First Half: 4x² -12x = 4x(x-3)

  • Second Half: -3x+9 -3(x-3)

Step Four: Identify the Factors

The last step is to identify the factors as shown in Figure 15 below.

 

Figure 15: The factors are (4x-3)(x-3)

 

Now, you can conclude that the factors of 4x² - 15x + 9 are (4x-3) and (x-3).

You can again use double distribution on (4x-3)(x-3) to verify that your solution is correct.

If you need more step-by-step help with how to factor polynomials with 3 terms when a does not equal 1, check out our free YouTube video tutorial.

Otherwise, continue on to the final section where you will learn how to factor polynomials with 4 terms.

How to Factor Polynomials with 4 Terms

The last section of this guide will cover how to factor polynomials with 4 terms and how to factor cubic polynomials.

In this section, we are going to apply a grouping method for how to factor a cubic polynomial that is very similar to the way that you factored trinomials when the leading coefficient, a, did not equal one in the last section. So, you may want to review that section before moving onto the 4 term polynomial factoring examples, however, it is not completely necessary, as we will be taking a step-by-step approach to solving two examples of factoring cubic polynomials.

Now, lets go ahead and work through our first example on how to factor cubic polynomials.

 

Figure 16: Polynomials with 4 terms are referred to as cubic polynomials.

 

Example #1: Factor 2x³ - 3x² + 18x - 27

For the first example, we have to factor the cubic polynomial: 2x³ - 3x² + 18x - 27

Step One: Split the cubic polynomial into groups of two binomials.

To factor this 4 term polynomial, we are going to apply what is called the grouping method, which requires you to split the polynomial into two groups (two separate binomials) with the goal of factoring a GCF out of each one.

 

Figure 17: How to Factor Cubic Polynomials by Grouping: The first step is to split the polynomial into two groups of binomials.

 

Remember that the goal is to create two separate binomials that have a GCF. If there is no apparent GCF, you have the option of swapping the positions of the middle terms (- 3x² and 18x), but that is not necessary for factoring this 4 term polynomial.

In this example, by the end of step one, you now have two groups to factor:

  • (2x³ - 3x²)

  • (18x - 27)

Step Two: Factor each binomial by pulling out a GCF

Now, go ahead and divide a GCF out of each binomial as follows:

  • (2x³ - 3x²) → x²(2x - 3)

  • (18x - 27) → 9(2x - 3)

This step is illustrated in Figure 18 below.

 

Figure 18: How to factor a cubic polynomial by grouping.

 

Step Three: Identify the factors

Notice that both results have a (2x-3) term. This is important and expected. If both results do not share a same term, then you either made a mistake or the polynomial with 4 terms is not factorable.

But, since we were able to factor each group by pulling out a GCF that resulted in both groups sharing a common factor of (2x-3), we know that we can factor out the other terms (x² and +9), so now have our factors: (x²+9) and (2x-3)

Final Answer: The factors of 2x³ - 3x² + 18x - 27 are (x²+9) and (2x-3)

The entire process of how to factor polynomials by 4 terms by grouping is illustrated in Figure 19 below.

 

Figure 19: The factors of 2x³ - 3x² + 18x - 27 are (x²+9) and (2x-3)

 

Example #2: Factor 3y³ + 18y² + y + 6

Let’s gain some more practice with how to factor a cubic polynomial by grouping by solving one more example problem.

In this case, we have to factor the cubic polynomial 3y³ + 18y² + y + 6 using the same grouping method as the previous example.

Step One: Split the cubic polynomial into groups of two binomials.

Start by splitting the cubic polynomial into two groups (two separate binomials).

 

Figure 20: Split the cubic polynomial into two groups of binomials and check to see if they can both be factored by pulling out a GCF.

 

As shown in Figure 20 above, by completing step one, you are left with these two groups

  • (3y³ +18y²)

  • (y+6)

Hold on! Before moving onto the next step, you should notice that the second group (y+6) cannot be factored by pulling out a GCF (because there is no greatest common factor between 1y and 6).

However, notice that we can swap the middle terms of the cubic polynomial (18y² and +y) as shown in Figure 21 below.

Now, we can factor a new 4 term polynomial 3y³ + y + 18y² + 6 that is equivalent to the original 4 term polynomial since the commutative property of addition allows you to rearrange the terms.

 

Figure 21: The commutative property of addition allows you to rearrange the middle terms when you are unable to group and GCF the original cubic polynomial.

 

Notice that you can split this new polynomial into two binomials that can be factored by pulling out a GCF:

  • (3y³ + y)

  • (18y² + 6)

 

Figure 22: After rearranging the original cubic polynomial, you can split it into two binomial groups that can be factoring by pulling out a GCF.

 

Step Two: Factor each binomial by pulling out a GCF

As illustrated in Figure 22 above, after rearranging the original cubic polynomial, you can split it into two binomial groups that can be factoring by pulling out a GCF as follows:

  • (3y³ + y) → y(3y² + 1)

  • (18y² + 6) → 6(3y² + 1)

Step Three: Identify the factors

Now, you can see that both factors have a (3y² + 1) term, which means that you have factored correctly.

Final Answer: The factors of 3y³ + 18y² + y + 6 are (y+6) and (3y² + 1)

The entire process of how to factor polynomials a cubic polynomial like the one in this example is illustrated in Figure 23 below.

 

Figure 23: How to factor cubic polynomials by grouping (step-by-step).

 

How to Factor Polynomials: Conclusion

Learning how to factor a polynomial is an important algebra skill that every math student must learn at some point.

While factoring polynomials can be tricky, there are several useful and effective strategies that you can use to factor polynomials. The strategy that you choose will depend on how many terms a polynomial has (as you will often be dealing with factoring polynomials with 2, 3, or 4 terms).

The best way to get better at factoring polynomials (especially cubic polynomials that have 4 terms) is by working through practice problems step-by-step. If you feel like you need more practice, we highly recommend working through the examples in this guide several times to gain more experience.

Keep Learning:

March Madness Perfect Bracket Odds—What are the Chances?

1 Comment

March Madness Perfect Bracket Odds—What are the Chances?

What are the March Madness Perfect Bracket Odds?

The Chances of a Perfect March Madness Bracket are Crazier Than You Might Think

 

Is this possible? What are the March Madness perfect bracket odds?

 

The annual NCAA College Basketball Tournament—known as March Madness—is one of the most exciting times of the year for college basketball fans. Every year, millions of fans across the United States fill out their tournament brackets, hoping to predict the winners of all 63 games. But what are the chances of filling out a perfect March Madness bracket? Is it even possible?

Let’s explore the math behind why a predicting a perfect March Madness bracket is essentially impossible by diving into the answers to the following questions:

 

Every year, millions of fans fill out a tournament bracket. What what are the chances of a perfect March Madness bracket?

 

What are the March Madness Perfect Bracket Odds?

Filling out a perfect March Madness bracket means correctly predicting the winner of all 63 NCAA basketball tournament games. Having a perfect bracket means that must be 100% correct in all of your picks, including all of the inevitable upsets (when a lower ranked team defeats a higher ranked team) that occur every year.

The mathematical probability of a perfect March Madness bracket are:

1 : 9,200,000,000,000,000,00.

You read that correctly. The chances of correctly predicting a perfect March Madness bracket are astronomically low. In fact, some mathematical models estimate the odds of having a perfect March Madness bracket at one in 9.2 quintillion.

To put it another way, you are more likely to win the lottery multiple times in a row or get struck by lightening twice on the same day than to fill out a perfect bracket.

 

Given the low odds of a perfect March Madness bracket, is it even possible?

 

Is a March Madness perfect bracket even possible?

The short answer is no, it is not possible to fill out a perfect March Madness bracket given the insanely high odds of correctly predicting the winner of all 63 games.

The reason for saying that a March Madness perfect bracket is impossible is simple—there are just too many variables at play in every game that make predicting winners incredibly difficult.

Even the most talented and experienced basketball analysts and sports statistics experts can not predict with complete accuracy how a given tournament game will play out. Factors such as injuries to key players, momentum swings, and elements of chance can all play a role in the outcome of a basketball game. And when you consider that there are 63 games in the tournament, the chances of getting correctly predicting the winner of every single game is virtually zero.

Of course, the fact that a perfect March Madness bracket is essentially impossible should not discourage you from filling out a bracket and attempting to correctly predict the outcome of as many games as possible. Why? Because filling out a bracket and chasing this impossible dream is what makes March Madness such a fun time of year for die-hard and casual basketball fans alike.

Even if you don't have a perfect bracket, you can still compete with your friends and colleagues to see who can get the most games right. And who knows? You might just run into some luck and make some accurate predictions that others did not.

 

Has there ever been a perfect March Madness bracket?

 

Has There Ever Been a Perfect March Madness Bracket?

Millions of basketball fans have been filling out March Madness brackets since the tournament’s inception in 1939, but has anyone ever had a perfect March Madness bracket?

The answer is no.

Remember that the odds of predicting the winners of all 63 tournament games are astronomically low, with some estimates placing the odds of a perfect bracket at around 1 in 9.2 quintillion.

Even with the rise of advanced analytics and machine learning algorithms, no one person has ever been able to achieve a perfect March Madness bracket, and they likely never will.

How Can You Use Math to Improve Your Bracket Predictions?

Mathematically speaking, filling out a perfect bracket is virtually impossible. But, what are your chances of getting a certain number of games right?

Let’s take a look at some statistics that will shed some light on this question.

According to the NCAA, the chances of correctly predicting the outcome of the first round (the 32 games played during the first two days of the tournament) are about 1 in 4.3 billion. While those odds are not very much in your favor, they are still way better than the odds of predicting a perfect March Madness bracket. In fact, there have been several occasions where someone correctly predicted the winners of all 32 first-round games.

 

The chances of predicting the winner of any NCAA tournament game depend on many factors including matchups, injuries, and past performance.

 

But, as the tournament continues on into the later rounds, the odds of correctly predicting every winner become exponentially smaller. By the time you get to the third round (known as the Sweet 16), the chances of predicting all the games correctly are about 1 in 75.6 million.

As for the point in the tournament when only four teams remain (known as the Final Four), the odds of predicting all games correctly drop to about 1 in 2.4 million.

These odds are only estimates, and the actual chances of getting each game right can vary depending on many factors. The point is that, while the chances of a perfect March Madness bracket are essentially zero, it is still possible to correctly predict winners and have fun competing with others.

In fact, if you were to simply guess the winner of every March Madness game at random, without any knowledge or analysis of college basketball, you would be mathematically expected to correctly predict around half of the total games (about 31.5 out of the 63 games).

So, what should you keep in mind when filling out your March Madness bracket? The best advice we can give is to focus more on making educated based on information such as a teams’ record, matchups, current injuries, and recent performance. You can also take advice from trusted sports analysts and experts that can offer valuable insights that will help you make decisions when filling out your bracket.

 

Given that the March Madness perfect bracket odds are pretty much impossible, you can let yourself off the hook and simply have fun filling out your bracket

 

Another thing to keep in mind about filling out your bracket is the occurrence of upsets—when a lower ranked team wins against a higher ranked team. Upsets are incredibly common in the NCAA tournament and they are one of the most fun and exciting aspects of March Madness.

With this in mind, don't be afraid to pick a few lower-seeded teams to defeat a higher-seeded opponent, especially during the first two rounds.

On a final note, given that the March Madness perfect bracket odds are impossible, you can let yourself off the hook and simply have fun filling out your bracket, knowing that it will likely get busted during the first round.

The unpredictability of the tournament is what contributes to the 'Madness'—so have fun and good luck!

More Free Resources You Will Love:

Free Winning Percentage Calculator—All Sports

Use this free Winning Percentage Calculator to find the WP% of any team or individual athlete in any sport.

Search Tags: march madness perfect bracket odds, chances of a perfect march madness bracket, perfect march madness bracket, odds of having a perfect march madness bracket, march madness perfect bracket, perfect march madness bracket odds, has there been a perfect march madness bracket, has anyone ever had a perfect march madness bracket, odds of a perfect march madness bracket, perfect bracket march madness

1 Comment

Exploring Positive and Negative Numbers: Elevation Activity

4 Comments

Exploring Positive and Negative Numbers: Elevation Activity

How to Use Positive and Negative Numbers to Represent Quantities in the Real-World

Exploring Elevation Above/Below Sea Level is Great Way to Explore Positive and Negative Numbers

 
 

Are you looking for a fun way to teach your students about the relationship between positive and negative numbers in a real-world context?

On its own, a mathematical topic such as how positive and negative numbers can be used together to describe opposite directions or values can be confusing and uninteresting to kids who often struggle to see how a topic applies to their world.

Relating mathematics to the real world helps students to understand the practical everyday applications of math, which makes learning math fun, engaging, and, most importantly, meaningful. Plus, understanding the connections between mathematics and real life can spark student interest in math and allow them to see how useful the subject truly is.

In this post, you will learn about a fun activity that explores the relationship between positive and negative numbers in the context of their elevation above or below sea level in comparison to other geographical locations.

(Do you want free K-8 math resources and activities in your inbox every week? Click here to sign up for our free math education email newsletter)

 

Positive and Negative Numbers Activity: What is My Current Elevation?

 

What is My Current Elevation?

Math Activity: What is My Current Elevation Above/Below Sea Level Compared to Other Locations?

Grade Level(s): 5th Grade, 6th Grade, 7th Grade

Learning Standard(s): Understand that positive and negative numbers are used together to describe quantities having opposite directions or values (e.g., temperature above/below zero, elevation above/below sea level, credits/debits, positive/negative electric charge); use positive and negative numbers to represent quantities in real-world contexts, explaining the meaning of 0 in each situation.

This activity helps students understand the concept of elevation, especially in the context of U.S. cities like New Orleans and Miami, which are at or below sea level, and Denver, known for being thousands of feet above sea level.

 

Click the link below to download the free pdf guide that accompanies this lesson.

 

The following activity lets students take a deeper look into finding the elevation of geographic locations with sea level as a reference point. In this case, the measurement tool will be a vertical number line where sea level is at zero. All locations above sea level will have positive elevation values and all locations below sea level will have negative elevation values.

To find the difference in elevation between two locations, students will have to add positive and negative numbers.

For example, to find the difference in elevation between Denver, Colorado (5,690 feet elevation) and New Orleans, Louisiana (-3 feet elevation), students would have to perform the following calculation:

  • 5,690 - (-3) = 5,690 + 3 = 5,693 foot difference in elevation

Why is Denver, Colorado called the Mile High City?

Why is New Orleans at such high risk of flooding?

The lesson is interactive and calls on kids to use Google Maps to research their own elevation and figure out how many feet higher or lower they are than my location in Rocky Mountain National Park in Colorado, which is where the video that corresponds with this lesson was filmed!

The lesson also has real world extension questions related to science, geology, and climate change.

Click the video link below to watch the free What is Your Elevation video guide for students and click here to download the free pdf student guide that accompanies the video lesson.

 
 
 
 

4 Comments