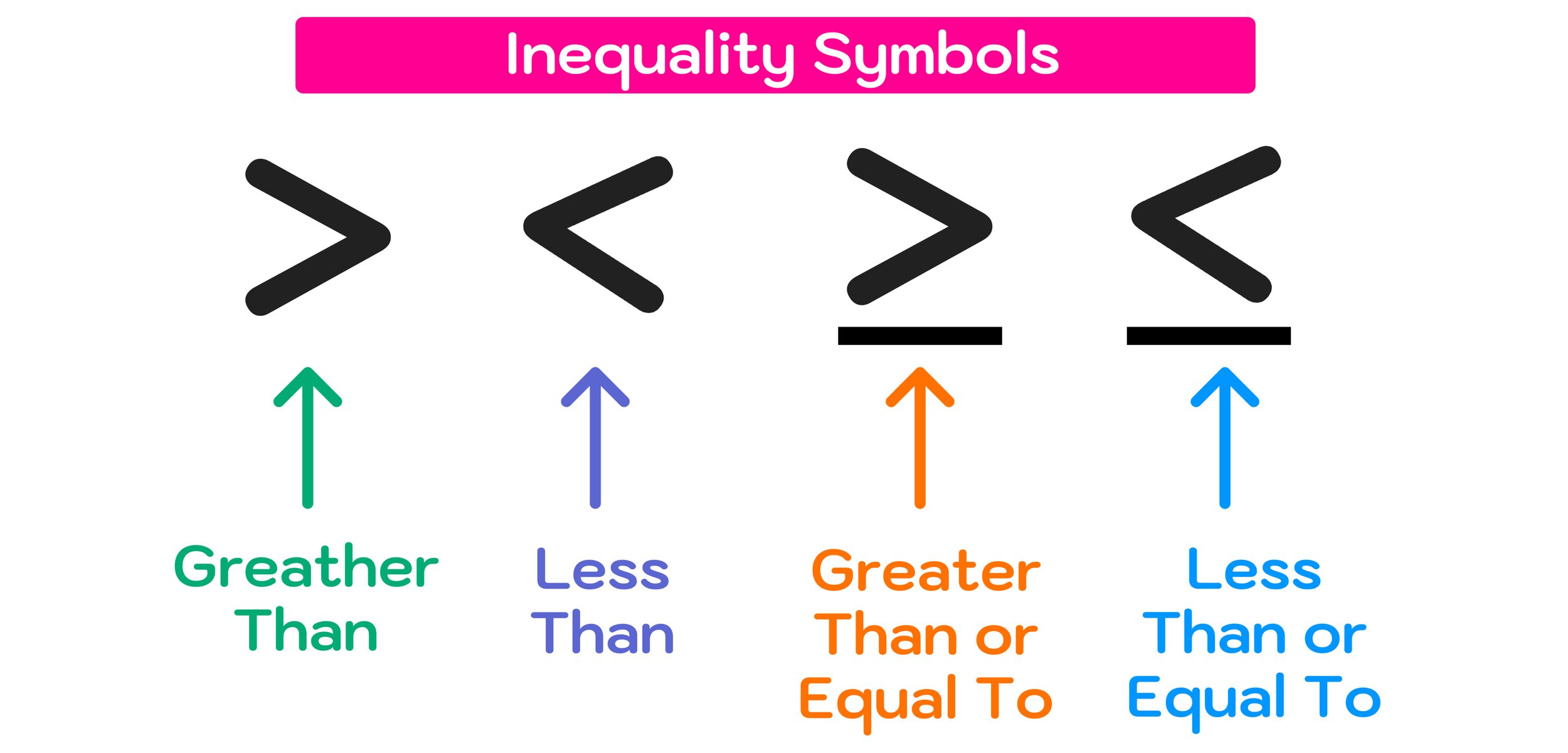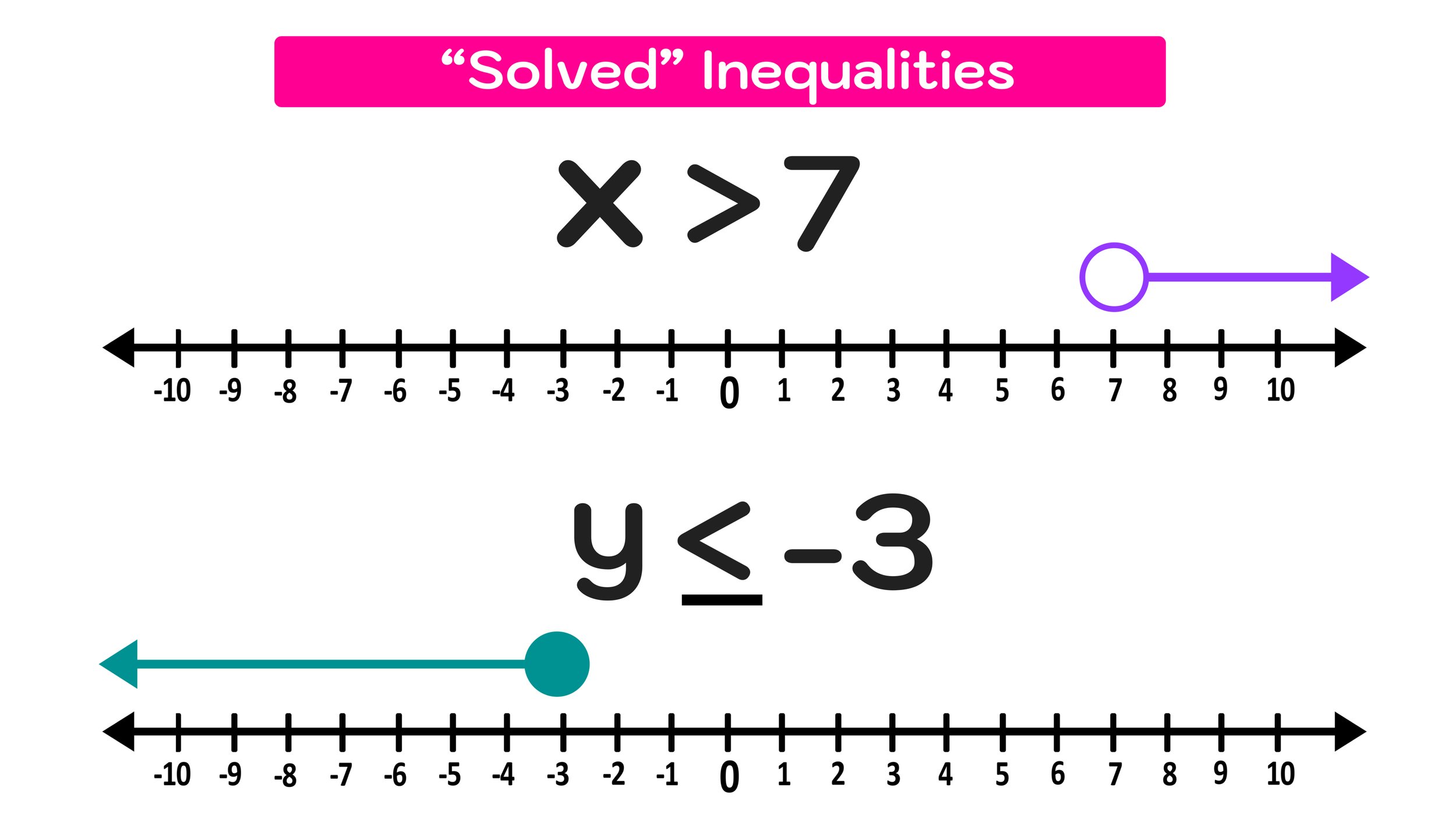What Color is Math?

What Color is Math?

What Color is Math?

A Deep Dive into the Colorful Subject that is Mathematics

 

What Color is Math?

 

It’s interesting to wonder “what color is math?” After all, mathematics is about digits, equations, shapes and figures, and logical thinking—not colors. In fact, most students would probably say that math is not related to colors at all and maybe even that math has no color. But would saying that math has no color be true? This post will take an open-minded exploration into mathematics and its often overlooked color palette.

We will start by looking into the relationship between mathematics and color as seen in history, everyday life, education, nature, and our emotions related to learning mathematics.

Finally, we will give a definitive answer to “what color is math?” as well as colors that best represent several fields of mathematics including algebra, geometry, and calculus.

The History of Math

Did you know that the earliest cultures that practiced mathematics actually associated colors with numbers and important math concepts? For example, the ancient Mayans used a color-coded system for their mathematical calendar cycles. Also, Chinese culture has attributed colors to numbers, which play a significant role in the field of numerology—especially for ancient Chinese culture, which believed that numbers could influence your fate and personal fortune in life. Given that the idea of mathematics having color has been present for so long, it makes exploring the questions, what color is math?, worthwhile.

 

Ancient Chinese mathematicians believed that numbers could influence your fate and personal fortune. (Image: Mashup Math MJ)

The ancient Mayans used a color-coded system for their mathematical calendar cycles. ( (Image: Mashup Math MJ)

 

Math in Every Day Life

In modern day life, we use colors to represent mathematical quantities and to categorize things all the time. For example, when it comes to driving, the color green means go and the color red means stop.

And when it comes to data, tables and figures are used to represent statistics and they rely on color to differentiate between quantities, categories, and events. A pie chart with each section being the same color would be useless, which is why colors are used to detail each different section.

Since colors help us to visualize and differentiate things, providing specificity, clarity, and comparison, they are an amazing tool that can be used in mathematics to help you to identify patterns, differentiate quantities, and display data in a way that is easy to analyze and understand.

 

What Color is Math? Data tables and charts rely on color to differentiate quantities and categories. (Image: Mashup Math FP)

 

Colors for Teaching Math

Math teachers often use colors to help their students to understand math in a variety of ways. For example, young students often use colorful hands-on resources such as fraction strips to develop deep conceptual understanding of a topic or skill.

The use of colors helps students to differentiate between values, compare and contrast them, and make conclusions. It is colors that allow students to engage with mathematics in a visual and tactile way, which fosters the development of math skills and connections.

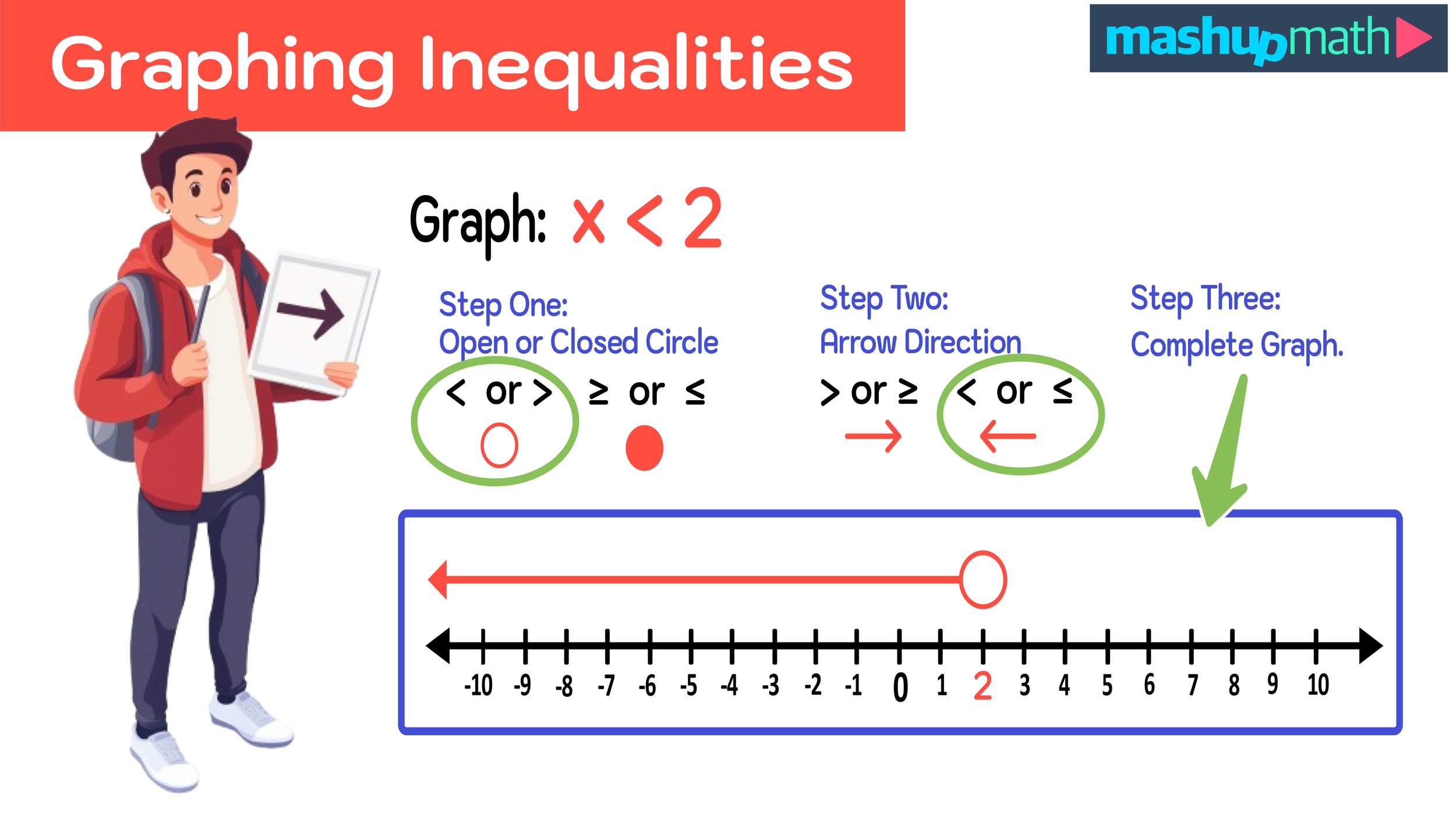
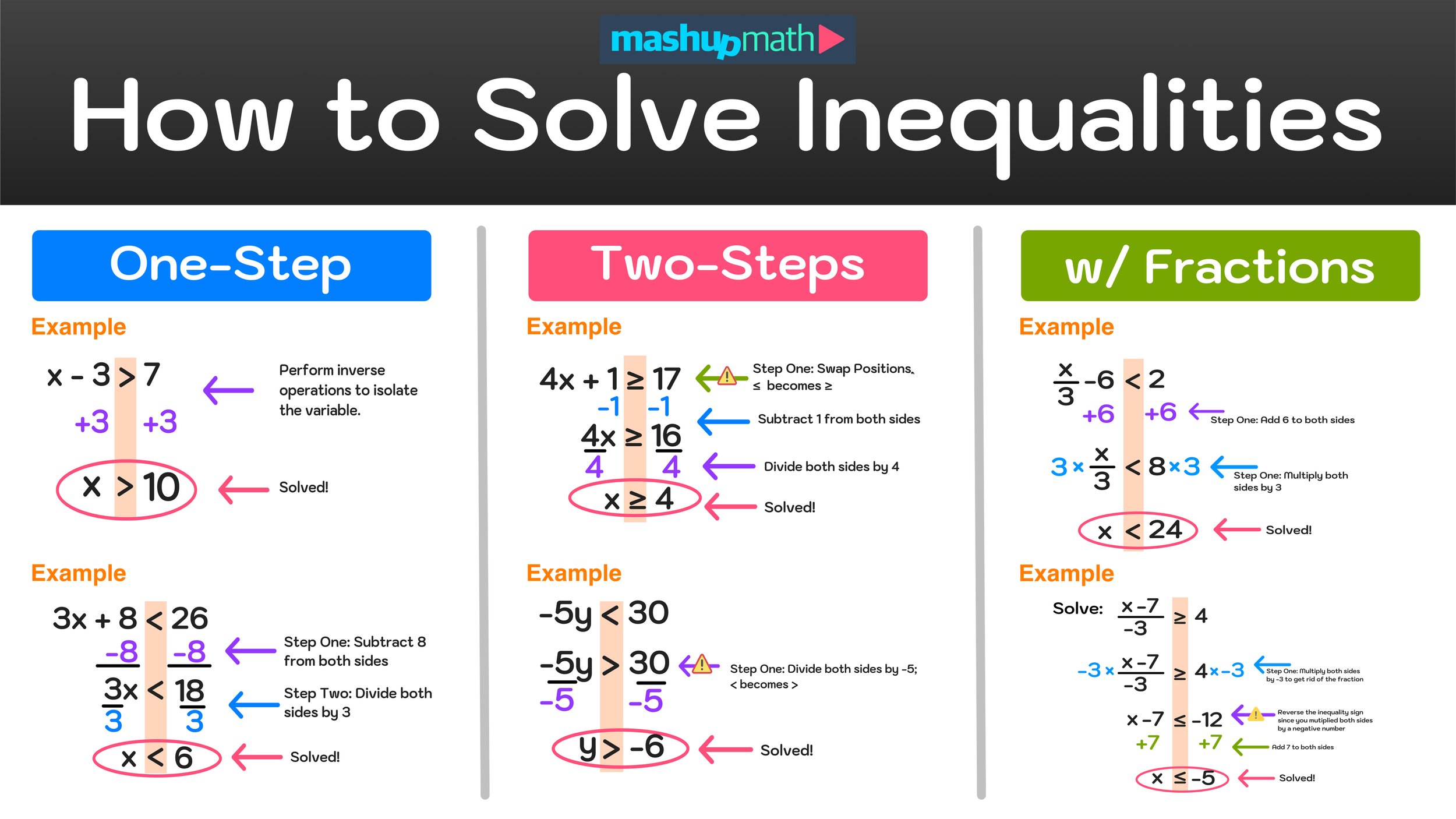
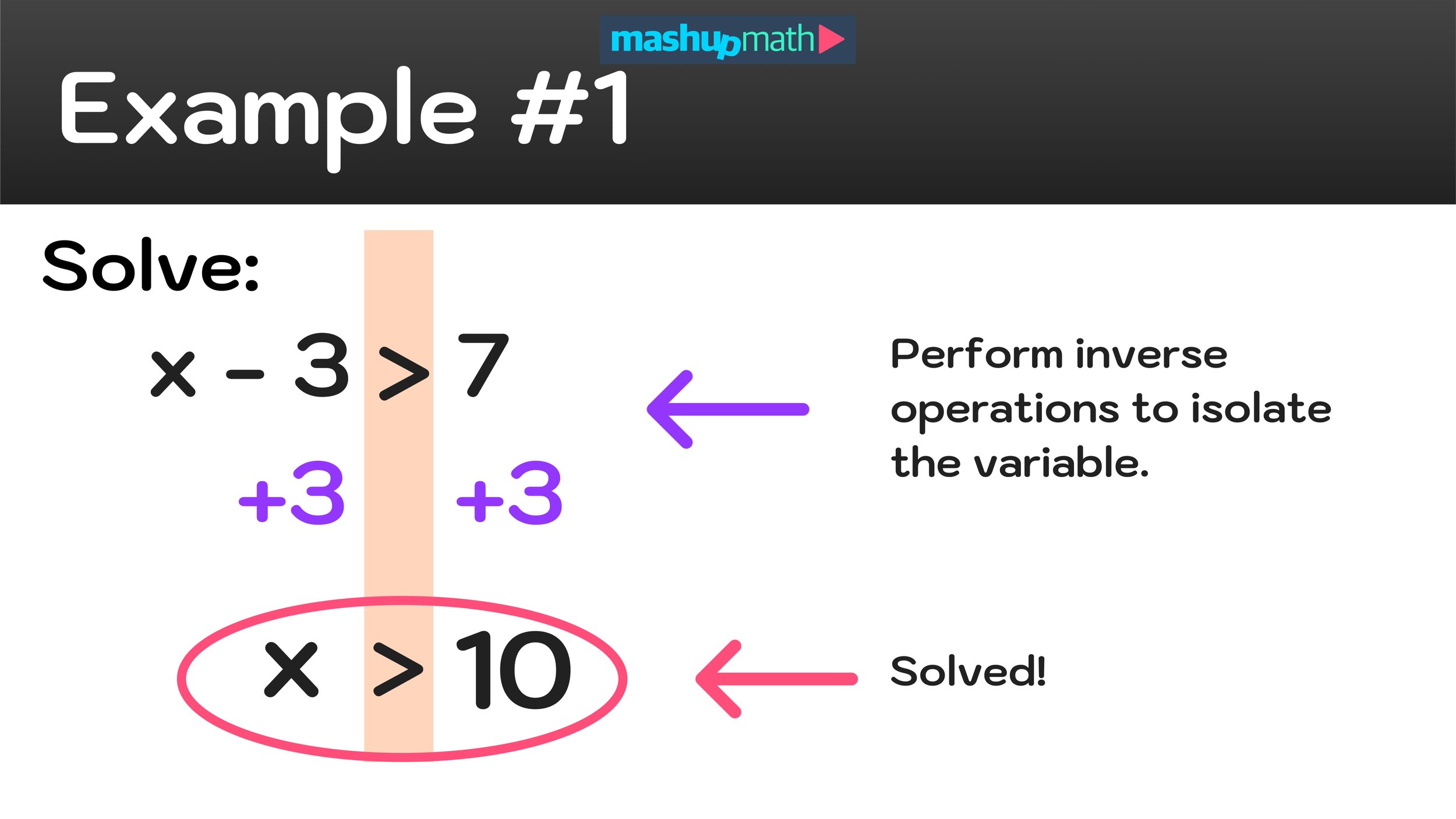
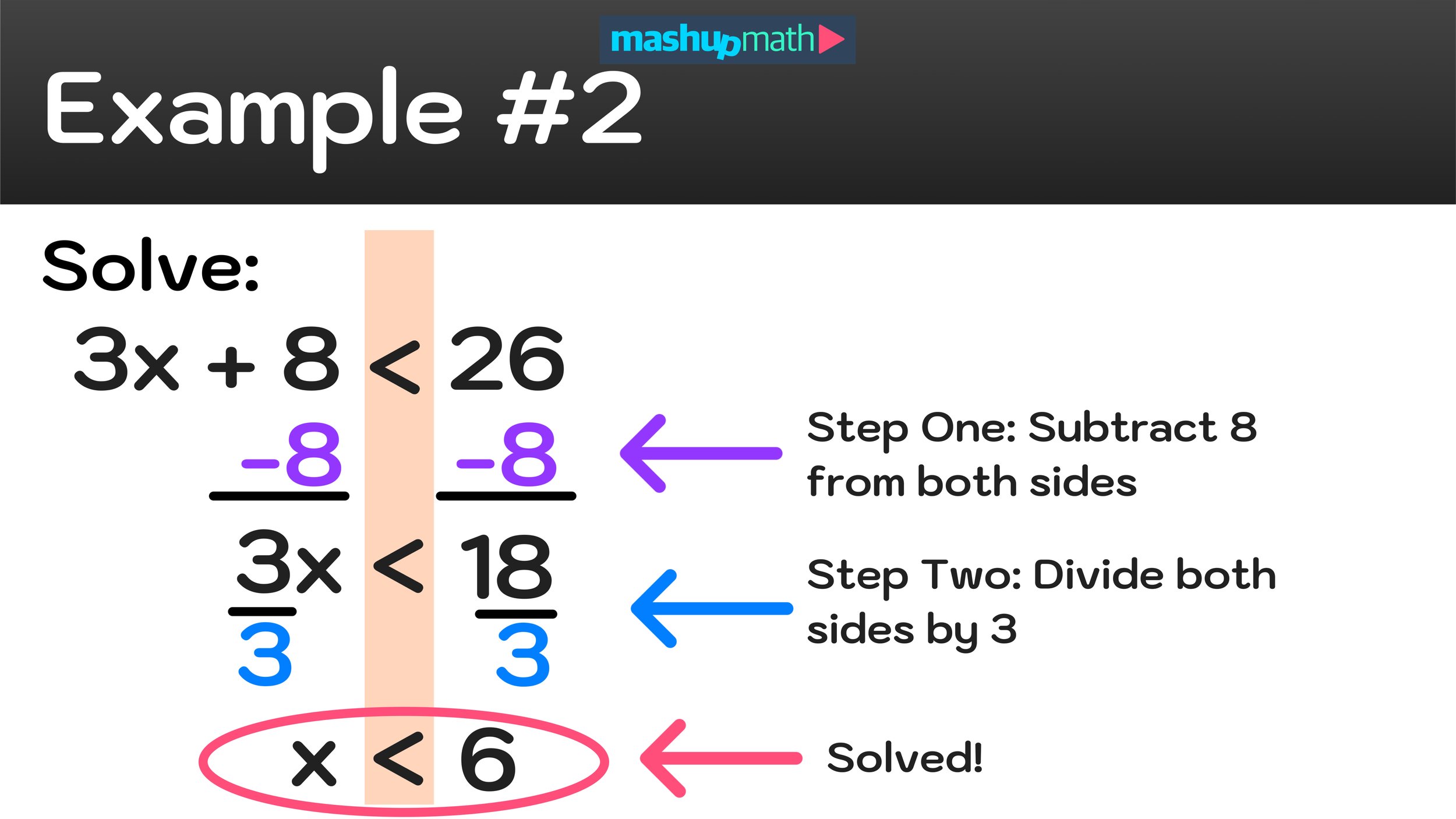
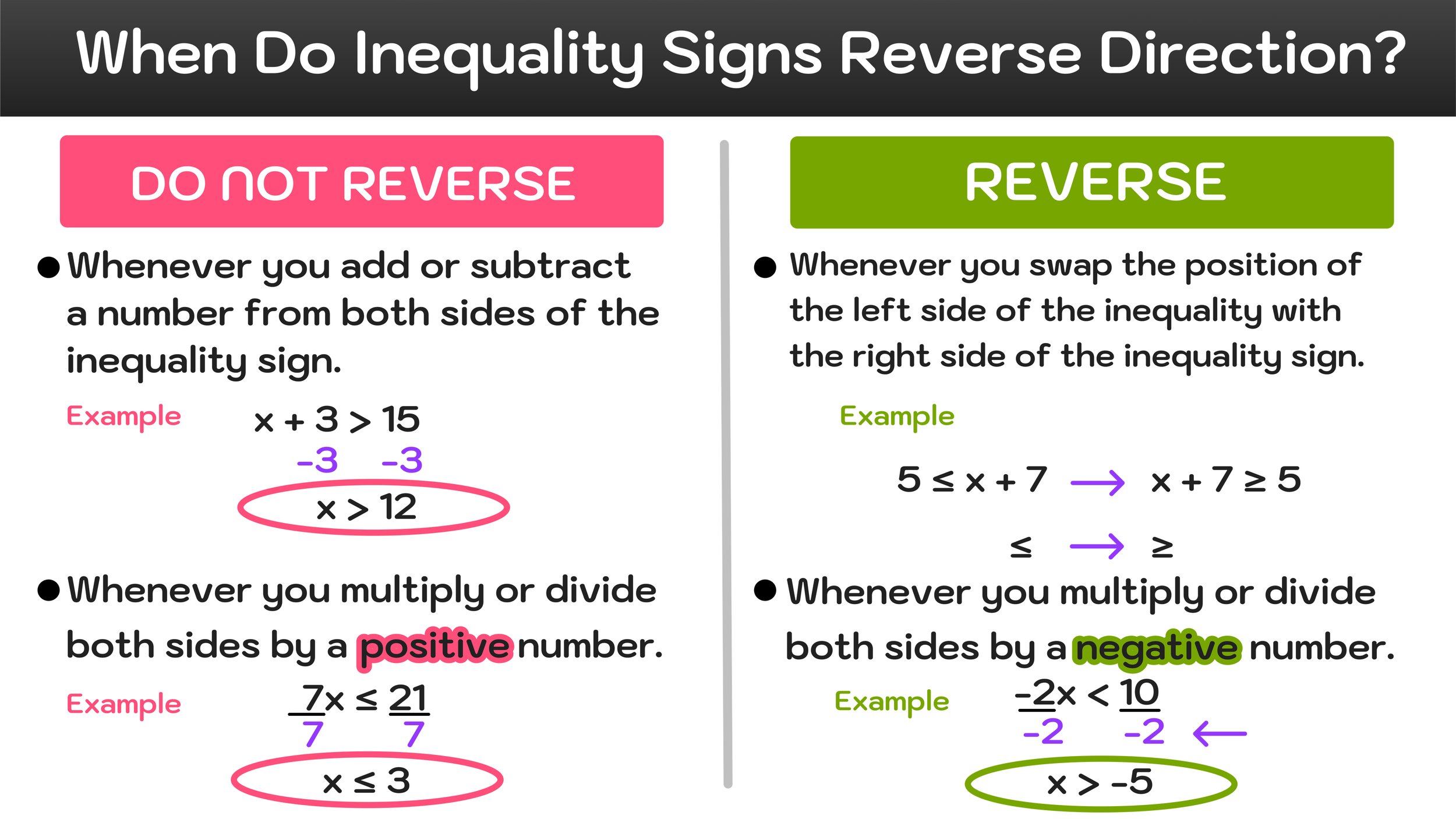
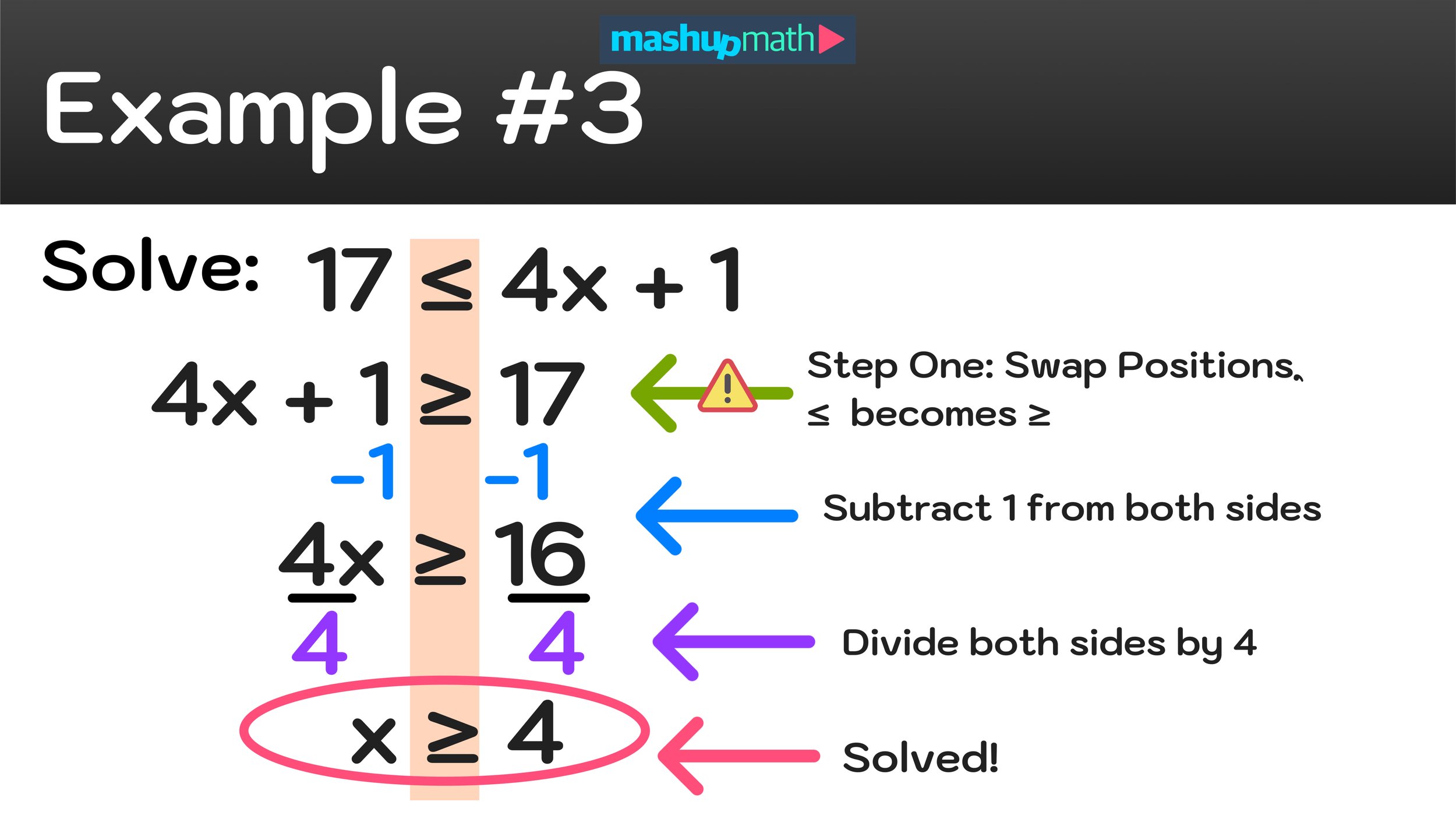
At higher levels of math, students can use colors to navigate multi-step problems such as performing proofs in Geometry, where complex diagrams can easily become impossible to read without the use of colors to differentiate each step. By looking at completed color-coordinated geometry proof, one could easily answer the questions “What color is math?” by saying that the subject in fact encompasses the entire rainbow.

Fraction Strips

Geometry Proofs

Math in Nature

What color is math? If we seek the answer to this question in nature, we will see a wide range of mathematical concepts naturally displayed in vivid color.

For example, the famous Fibonacci sequence—a series of numbers where every number is the sum of the two numbers preceding it, can be seen in the spirals or buds of Romanesco Broccoli. In this case, the answer to the question “What color is math?” is green! When it comes to observing the Fibonacci sequence in the heads of sunflowers, you could say that math is vibrant yellow or golden orange. And in the case of pinecones, you could say that math is a deep woody brown.

These types of fractals are amazing displays of mathematics in nature and their associated colors are more than just something pretty to look at—the colors themselves are expressions of mathematics and they help us to understand the nature of mathematical series and sequences in our world.

Romanesco Broccoli

Photo by VENUS MAJOR on Unsplash

Sunflowers

Photo by Paul Green on Unsplash

Pinecones

Photo by Vishwasa Navada K on Unsplash

Math and Emotions

Now that you are more familiar with the relationship between mathematics and color in history, everyday life, teaching, and nature, it’s time to think about the role that colors play in thoughts, feelings, and emotions when we interact with math.

Mathematics is, after all, a subject that is practiced by humans who are emotional creatures. By exploring the question “What color is math?” we are actually expanding our understanding of it because we are thinking about the subject in a more creative way.

Of course there is no one correct answer, but it would be a fruitful exercise to consider the colors of your emotions when you perform mathematical tasks such as:

  • Vibrant Gold: When you finally solve that challenging problem

  • Deep Blue: When you are learning something new, thinking deeply, and concentrating

  • Bright Red: When you are struggling with a concept and feeling frustrated and/or anxious.

Because math learners will experience all of these emotions as well as everything in between, we can say that the color of math is truly the full spectrum of colors.

Frustration

(Image: Mashup Math MJ)

Concentration

(Image: Mashup Math MJ)

Success

(Image: Mashup Math MJ)

Answer: What Color is Math? 🟨

Here we will do our best to give a definitive answer to the question “What color is math?”

Mathematics as a subject does not inherently have a designated color, but we can assign it one given its attributes.

Based on our subjective interpretation of mathematics, if we had to assign it to one color, vibrant gold would be extremely fitting. Since the color gold represents timeless beauty, value, and universality, you could say that mathematics is a universal and golden tool that helps us to explain the universe. Gold has been a standard of value for millions of years, just as math remains the cornerstone of science and progress.

If we had to assign it to one color, vibrant gold would be extremely fitting. Since the color gold represents timeless beauty, value, and universality.

With the same subjective approach in mind, we can also state the colors of six key branches of mathematics:

  • 🔵 Algebra is Blue: Since the color blue is associated with logical thinking and clarity, it fits well with the analytical and logical processes associated with algebraic problem solving.

  • 🟢 Geometry is Green: Since geometry is the study of shapes and their positions in space and relationships between figures and objects, green is fitting because it is associated with balance, harmony, nature and growth.

  • 🟠 Trigonometry is Orange: Trigonometry is the study of waves and cyclic relationships, where there is inherent energy and rhythm. Since orange is a blend of red (symbolizing intensity) and yellow (symbolizing brightness and forward progress), orange is a fitting color.

  • ⬜ Calculus is Gray: The color gray does not mean boring in this case. In an elegant way, gray balances the properties of both black and white, just as the field of calculus balances quantities that are both infinitely small and infinitely large. Calculus also deals with the continuous spectrum of numbers and values and includes instances of infinity and absolute nothingness, just as black is the absence of color and white is the sum of all colors.

  • 🟡 Number Sense is Yellow: Yellow often represents energy, insight, and discovery. This elementary math topic is focused on developing a sense for numbers and their relationship to each other. Number sense is foundational and grasping it will light the way for young students to take on more challenging and complex math concepts in the future.

  • 💠Statistics and Probability are Teal: Since statistics and probability are a blend of two topics:

    data analysis and predicting the likelihood of future events, the blend of blue and green that is teal is a solid fit. The blue aspect represents logic and systemic problem solving while the green aspect represents unpredictability and variability in a logic vs. nature dynamic.

 

What color is math?

 

Conclusion

If you were looking for a single answer, then you may be disappointed. While math and color go hand-in-hand, it is impossible to say that mathematics is any one color.

In fact, it would be more appropriate to say that math is every color. At times, math is colored red for passion and persistence. At others, math is colored blue for deep thinking and concentration. Sometimes math glows in golden yellow for discovery and enlightenment and at others a deep forest green for nature and wisdom. And when math is not those colors, it is a kaleidoscope of all of the shades and hues that exist between them.

In conclusion, mathematics is a beautiful subject that can change and morph between the full spectrum of colors, which is why it continues to captivate us and allow us to better understand our universe.

More Free Resources You Will Love:

Why Am I So Bad at Math? (And How to Get Better)

If you are wondering, why am I so bad at math? The fault is likely due to you having a fixed mindset for learning, which is often a product of being negatively affected by harmful misconceptions about your ability to learn math.

How to Solve Inequalities—Step-by-Step Examples and Tutorial

3 Comments

How to Solve Inequalities—Step-by-Step Examples and Tutorial

How to Solve Inequalities Explained

Step-by-Step Guide: How to Solve an Inequality Equation

 

Free Step-by-Step Guide: How to solve inequalities and inequality equations

 

In math, an inequality is a symbol that is used to represent the relationship between two values or expressions that are not necessarily equal to each other. There are four types of inequality symbols:

  • > : greater than

  • < : less than

  • ≥ : greater than or equal to

  • ≤ : less than or equal to

Understanding how to solve inequalities is an important math skill that all students will need to be successful in algebra and beyond. To acquire this skill, you will have to build upon your knowledge of solving equations and extend that understanding to solving inequalities.

This free Step-by-Step Guide on How to Solve Inequalities covers the following:

While learning how to solve an inequality is a little trickier than learning how to solve an equation, you can easily learn how to solve inequalities by working through this guide. By working through the step-by-step practice problems below, you will gain plenty of helpful practice with solving inequalities, which will put you on the path of being able to solve any inequality with ease.

While you are probably eager to dive into a few practice problems, let’s start off with a quick review of a few key vocabulary terms that you should deeply understand before you begin learning how to solve an inequality.

 

Figure 01: There are four types of inequality symbols: > : greater than, < : less than, ≥ : greater than or equal to, and ≤ : less than or equal to.

 

What is an inequality?

As said earlier, in math, an inequality is a relationship between two values or expressions that are not equal to each other. Because the values or expressions are not equal to each other, we have to use an inequality sign instead of an equals (=) sign.

You already know that there are four types of inequalities: > : greater than, < : less than, ≥ : greater than or equal to, and ≤ : less than or equal to (these four types of inequalities are illustrated in Figure 01 above).

Basic inequalities do not need to be solved since the variable is already by itself.

For example, consider the inequalities x>7 and y≤-3.

These inequalities can be thought of as solved because the variables are already on their own. These “solved” inequalities are illustrated in Figure 02 below.

 

Figure 02: How to solve inequalities. What do solved inequalities look like?

 

But, what if we had an inequality that looked like this: x - 3 > 7

Since the variable, x, is not by itself, this inequality still needs to be solved, and the remainder of this guide will show you exactly how to do that.

Now that you are familiar with the key vocabulary terms, it’s time to look at a few examples.

How to Solve Inequalities Example #1

Example: x - 3 > 7

Just as you would solve an equation, to solve an inequality, you must use inverse operations to isolate the variable, which, in this example, is x.

You can isolate x easily by adding 3 to both sides of the inequality sign as follows:

  • x - 3 > 7

  • x -3 + 3 > 7 +3

  • x > 10

Now the inequality is solved! The answer is x>10. The step-by-step procedure to solving this first example is illustrated in Figure 03 below.

 

Figure 03: How to solve an inequality: x-3>7

 

This first example of how to solve inequalities was relatively simple and only took one step to solve. Now, let’s move onto solving a slightly more difficult inequality.

How to Solve Inequalities Example #2

Example: 3x + 8 < 26

Again, to solve the inequality you have to isolate the variable x by performing inverse operations as follows:

  • 3x + 8 < 26

  • 3x - 8 < 26 - 8

  • 3x < 18

  • 3x/3 < 18/3

  • x < 6

Solving this example required two steps (step one: subtract 8 from both sides; step two: divide both sides by 3). The result is the solved inequality x<6.

The step-by-step procedure to solving example #2 is illustrated in Figure 04 below.

 

Figure 04: How to solve an inequality: 3x+8<26

 

When Do Inequality Signs Reverse Directions?

The first two examples of solving inequalities are considered basic and they can both be solved in two steps or less.

However, more complex inequalities can include instances when the inequality sign will reverse direction in one of the following ways:

  • > becomes <

  • < becomes >

  • ≥ becomes ≤

  • ≤ becomes ≥

So, when do you have to worry about reversing the direction of an inequality sign?

Let’s start by listing all of the instances when you are safe and do not have to change the direction of the inequality sign.

  • Whenever you add or subtract a number from both sides of the inequality

  • Whenever you multiply or divide both sides of the inequality by a positive number

Both of these cases occurred in examples #1 and #2, which is why we did not have to change the direction of the inequality sign.

However, you do have to change the direction of the inequality sign under these instances:

  • 🔄 Whenever you swap the position of the left side of the inequality with the right side of the inequality

  • 🔄 Whenever you multiply or divide both sides of the inequality by a negative number

These rules are illustrated in Figure 05 below.

 

Figure 05: When do inequality signs reverse direction?

 

Now, let’s take a look at a few examples of solving inequalities where you will have to reverse the direction of the inequality sign.

How to Solve Inequalities Example #3

Example: 17 ≤ 4x + 1

This example is a bit different because the variable, x, is on the right side of the equal sign and we typically express solved inequalities with the variable on the left.

You can still solve this problem the same way that you solved example #2, but first you must swap the left side of the inequality with the right side. However, remember that swapping the position of the left side and the right side requires you to also reverse the direction of the inequality as follows:

  • 17 ≤ 4x + 1 ➙ 4x + 1 ≥ 17

⚠️ Notice that the ≤ reversed position to become ≥!

Now, you can solve 4x + 1 ≥ 17 as follows:

  • 4x + 1 ≥ 17

  • 4x + 1 -1 ≥ 17 -1

  • 4x ≥ 16

  • 4x/4 ≥ 16/4

  • x ≥ 4

The inequality has been solved and the final result is x ≥ 4.

The steps for solving example #3 are detailed in Figure 06 below.

 

Figure 06: How to solve an inequality when the variable is on the right.

 

Now that we have covered the first instance of when you have to reverse the direction of an inequality sign, let’s see an example of the second instance—Whenever you multiply or divide both sides of the inequality by a negative number.

How to Solve Inequalities Example #4

Example: -5y < 30

Solving this inequality will require only step to isolate the variable, y, on the left side of the inequality. However, since that one step involves multiplying or dividing by a negative number, you must also reverse the direction of the inequality sign as follows:

  • -5y < 30

  • -5y/-5 > 30/-5 (⚠️ since you divided by a negative, < becomes >)

  • y > -6

The inequality has been solved and the final result is y > -6.

The steps for solving example #4 are detailed in Figure 07 below.

 

Figure 07: How to solve an inequality when you have to multiply or divide both sides by a negative number.

 

How to Solve Inequalities with Fractions

Now that you have some more experience with solving inequalities and you know when you have to reverse the direction of the inequality sign, let’s take a look at two more complex examples that involve fractions.

How to Solve Inequalities with Fractions Example #5

Example: x/3 - 6 < 2

When it comes to solving inequalities with fractions, the same strategy as the previous examples will apply. To solve, you have to use inverse operations to isolate the variable on the left side of the equation.

And, if you have to swap the positions of the left and right sides of the inequality or if you multiply or divide both sides by a negative number, then you will have to reverse the direction of the inequality sign.

You can solve this inequality as follows:

  • x/3 - 6 < 2

  • x/3 -6 +6 < 2 + 6

  • x/3 < 8

  • 3 x (x/3) < 3 x (8)

  • x < 24

The inequality has been solved and the final result is x < 24.

*Note that this example did not require you to reverse the direction of the inequality sign since you did not have to swap positions or multiply/divide by a negative number.

The step-by-step process for solving example #5 is shown in Figure 08 below.

 

Figure 08: Solving Inequalities with Fractions Example #5

 

How to Solve Inequalities with Fractions Example #6

Example: (x-7)/-3 ≥ 4

This next example is the most complex one we have seen so far, but our strategy of using inverse operations to isolate the variable remains the same.

You can solve this inequality as follows:

  • (x-7)/-3 ≥ 4

  • (x-7)/-3 x -3 ≥ 4 x -3 (multiply both sides by -3 to get rid of the fraction)

  • x-7 ≤ -12 (⚠️ because you multiplied both sides by a negative, ≥ becomes ≤)

  • x-7 +6 ≤ -12 +7

  • x ≤ -5

The inequality has been solved and the final result is x ≤ -5.

⚠️ Note that we did have to reverse the inequality sign from ≥ to ≤ because we multiplied both sides by negative 3.

The step-by-step process for solving example #5 is shown in Figure 09 below.

 

Figure 09: Figure 08: Solving Inequalities with Fractions Example #6

 

As we enter the last section of this step-by-step guide to solving inequalities, let’s take a look at two more multi-step examples. If you can solve these next two problems using the previously discussed strategies, then you will be able to solve almost any problem related to solving inequalities.

How to Solve Inequalities with Fractions Example #7

Example: -6 > (7y-5)/9

This example will require a few steps in order to isolate the variable x, but we can still used inverse operations to solve as follows:

  • -6 > (7y-5)/9 ➙ (7y-5)/9 < -6

⚠️ Notice that the variable, y, is on the right side of the inequality sign, so we will start by reversing the positions of the left side and the right side, which also means that we have to reverse the direction of the inequality sign.

  • (7y-5)/9 < -6

  • (7y-5)/9 x 9 < -6 x 9

  • 7y-5 < -54

  • 7y -5 +5 < -54 + 5

  • 7y < -49

  • 7y ÷ 7 < -49 ÷ 7

  • y < -7

The inequality has been solved and the final result is y < -7.

Note that we did not have to reverse the inequality sign because the number that we multiplied both sides of the equation by was a positive 9.

The step-by-step process for solving example #7 is shown in Figure 10 below.

 

Figure 10: Solving Inequalities with Fractions Example #7

 

How to Solve Inequalities with Fractions Example #8

Are you ready for one final example of how how to solve inequalities with fractions? This one is a little tricky, but you have all of the tools that you need to solve it as long as you take it step-by-step.

Example: -5x - 6 ≤ (x+17)/-2

The first thing that you are probably noticing is that there are x’s on both sides of the inequality sign. Since the goal is to isolate x on the left side of the inequality, you will have to use inverse operations to get x by itself.

Let’s start by getting rid of the fraction on the right side of the inequality by multiplying both sides by -2.

  • -2(-5x - 6) ≤ (x+17)/-2(-2)

To solve the right side of the inequality, you will have to use the distributive property to multiply both terms (-5x-6) by -2.

  • 10x + 12 ≥ x+17 ⚠️

⚠️ And because we just multiplied both sides by a negative number, we had to reverse the direction of the inequality sign, so ≤ became ≥

Now we can continue solving this inequality by using inverse operations:

  • 10x + 12 ≥ x+17

  • 10x + 12 -12 ≥ x +17 -12 (move the constants to the right side)

  • 10x ≥ x + 5

  • 10x -x ≥ x -x +5 (move the variables to the left side)

  • 9x ≥ 5

  • 9x ÷ 9 ≥ 5 ÷ 9 (isolate x)

  • x ≥ 5/9

The inequality has been solved and the final result is x ≥ 5/9.

Note that it’s totally fine for our final result to be a fraction.

The step-by-step process for solving example #8 is shown in Figure 11 below.

 

Figure 10: Solving Inequalities with Fractions Example #8

 

Free Solving Inequalities Worksheet (w/ Answers)

Are you looking for some extra independent practice on how to solve inequalities and how to solve inequalities with fractions?

You can use the link below to download a free solving inequalities worksheet pdf file that includes a complete answer key. We recommend that you work through each problem on your own keeping this guide close by as a reference.

▶ Download your free Solving Inequalities Worksheet (One-Step) PDF

▶ Download your free Solving Inequalities Worksheet (Two-Steps) PDF

 

Preview: Solving Inequalities Worksheet PDF

 

While you work through the practice problems, keep the lesson summary main points below in mind.

Conclusion: How to Solve Inequalities

  • Like equations, inequalities can be solved by using inverse operations to isolate a variable on the left side of the inequality.

  • Solving an inequality by adding/subtracting numbers on both sides of the inequality or by multiplying/dividing both sides by a positive number does not result in a reversal of the inequality sign.

  • ⚠️ On the other hand, swapping the positions of the left and right sides of an inequality or multiplying/dividing both sides by a negative number requires you to reverse the position of the inequality sign such that: > becomes <, < becomes >, ≥ becomes ≤, and ≤ becomes ≥

  • When solving inequalities with fractions or inequalities with variables on both sides, the process of using inverse operations to isolate the variable and solve remains the same, albeit with a few more steps involved.

Keep Learning:

3 Comments

21 Silly Back to School Jokes for Kids!

Comment

21 Silly Back to School Jokes for Kids!

21 Silly Back to School Jokes for Kids

Are you ready for 21 side-splitting back to school jokes!?

 

Image: Mashup Math FP

 

Summer vacation is coming to an end, and that means that back to school season is officially upon us.

And while back to school season comes with the stress of preparing for a new school year, buying new clothes and supplies, and major schedule changes for students, parents, and teachers alike, this time of year doesn’t have to be all bad.

If you’re looking to share some fun and cheer this back to school season, then you’ll love our collection of the 21 funniest and silliest back to school jokes for kids.

(Did you hear the one about how bees get to school?…they take the school buzz! ;)

So, whenever you and your kids are ready to laugh and have some fun celebrating the end of summer and the start of a brand new school year, continue reading to see some of the funniest back to school jokes that you will find anywhere on the internet.

Back to school season only lasts a few short weeks and this is your best opportunity of the year to share some school-themed jokes and puns (including a few epic back to school dad jokes as well). No matter your age or your kids', this collection of back to school jokes offers something for everyone. We promise that you won’t be able to get through this collection of jokes without laughing out loud at least a few times.

Our collection of back to school jokes below includes each joke expressed in written form (the opening line is emboldened and the punch line is shown in italics) and several of the jokes include a corresponding image graphic that includes a cartoon-style representation of the joke that you can share in your classroom or on social media.

Without further delay, it’s time to chuckle. To enjoy all of our back to school jokes for kids, simply scroll down and let the back to school fun begin!

21 Silly Back to School Jokes

1.) Why did the math book look so sad?

Because it had too many problems!

Back to School Jokes for Kids (Image: Mashup Math)

2.) What is a snake’s favorite subject in school?

Hisssss-tory!

3.) Why did the student bring a ladder to class?

So he could make it to High School!

4.) What did the one pencil say to the other?

Don’t we look sharp today!

back to school jokes for kids

Back to School Jokes for Kids (Image: Mashup Math)

5.) What did the calculator say to the worried student?

Don’t worry, you can always count on me!

6.) Why did the student eat her assignment?

Because her teacher said it was a piece of cake!

7.) What is the king of all school supplies?

The Ruler!

Back to School Jokes for Kids (Image: Mashup Math)

8.) Why did the teacher wear sunglasses to school every day?

Because her students were too bright!

9) Why did the teacher take away a student’s scisccors?

So he couldn’t cut class!

10.) How do bees get to school?

They take the school buzz!

Back to School Jokes for Kids (Image: Mashup Math)

11.) How does a math teacher mow their lawn?

With a pro-tractor!

12.) What did the paper say to the pencil?

Write-on, Bro!

13.) How do you get straight A's?

By using a ruler!

14.) Why did the vocabulary book look so confused?

Because it lost its words!

15.) Are all monsters bad at math?

Not unless you Count Dracula!

Back to School Jokes for Kids (Image: Mashup Math)

16.) Why was the school cafeteria’s clock always behind?

Because it was taking too many lunch breaks.

17.) What did the paper say to the eraser?

I feel wiped out when I spend time with you!

18.) What is a history teacher's favorite fruit?

Dates!

19.) Why was the cyclops such a good teacher?

He only had one pupil!

Back to School Jokes for Kids (Image: Mashup Math)

20.) What did the eraser say after the first day of school?

I don’t think I’m going to make it to graduation!

21.) Why was the chalk so excited on the first day of school?

Because it was ready to make its mark!

How to Use These Back to School Jokes with Your Students

Now that you’ve had a chuckle or three, it’s time to plan how you will use some of the above back to school jokes with your students during the first week of school.

The first days of a new school year are filled with excitement, anxiety, and anticipation for teachers and students alike. With so much going on, a great strategy for taking the edge off and making your students feel more welcome and at ease is to include some humor in your first week of school lesson plans. And including a few of our back to school jokes and puns is a great way to get your students laughing and feeling positive about being a member of your class.

For ideas on how to incorporate back to school jokes into your upcoming lessons, here are a few suggestions:

  • Start the day off with a joke. One easy way to inject some humor into your classes is to choose your five favorite back to school jokes for kids from the list above and share one with your class to start the day every day for the entire first week of school. This is a simple way to get students to look forward to your class, fostering a positive outlook for the remainder of the school year.

  • Break the ice. If your students happen to be quiet and reserved at the start of the school year, sharing a few silly or corny back to school jokes is a great way to break the ice during the first week of the school year.

  • Add jokes into your lessons. If applicable, you can add some humor to your lesson plans by incorporating on-topic jokes related to whatever topic or subject you are teaching that day.

  • Create a joke bulletin board. Looking for classroom decoration ideas? If you have space in your classroom, consider posting a joke bulletin board where you can print and share your favorite back to school jokes. You can also allow students the opportunity to present their own school-themed jokes that you can post as well.

  • Add humor to your digital communication. Do you have a teacher website or an email newsletter? Silly back to school jokes can be shared outside of the classroom with fellow teachers and parents by including them in your digital communications. If you have a teacher website or an email newsletter, you can easily add your favorite joke as a way of incorporating some light humor into your communications.

  • Friday reflection. The first week of school can sometimes feel like it lasts an entire month. When the craziness settles and the first Friday arrives, students will be eager to reflect and share their feelings and experiences related to the first week of school. One great way to get that conversation started is to have students share which joke was their favorite and how humor helped them feel more at ease during the chaotic first week of school. This simple activity gives students an opportunity to express their feelings and lets them know that your classroom is a safe and open environment for sharing ones thoughts and opinions.

In conclusion, including a few fun back to school jokes during the first week of school this year is a fun and useful strategy for easing your students into a new school year and showing them that your classroom is a fun and engaging environment for interaction and learning. By incorporating humor when appropriate, teachers can show their students that school is an enjoyable place and one that they should look forward to returning to day in and day out.

Want More Funny Math Jokes?

Then you’ll love this ultimate collection of the funniest, zaniest, wackiest, and silliest math jokes and puns for all ages! Click here to get your math jokes today!

More Posts You Will Enjoy:

Did we miss your favorite back to school joke or pun? Share your thoughts and suggestions in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

Comment

5 Cause and Effect Examples and Explanations

5 Cause and Effect Examples and Explanations

Cause and Effect Examples and Explanations

5 Examples of Cause and Effect in Life, Nature, Math, and Literature

What are examples of cause and effect relationships? (Image: Mashup Math via Getty)

Whether you realize it or not, the continuous flow of events that make up everyday life are all driven by cause and effect relationships.

Whenever one specific action or event leads to another, cause and effect is at play. This relationship between an action and/or event and the directly resulting consequence or outcome is the foundation of the concept of cause and effect.

In this post, we will analyze 5 unique cause and effect examples to help you to better understand cause and effect relationships and how they work.

What is Cause and Effect?

Before we take an in-depth look at a few cause and effect examples, it’s important that you first understand the exact definition of a cause and effect relationship.

So, what is cause and effect?

Definition: A cause and effect relationship is the interaction between actions or events where one action or event (the cause) is the trigger that results in another action or event (the effect). In a cause and effect relationship, the effect is the result of the cause.

 

Definition: What is cause and effect?

 

This A➔B relationship is fundamental to understanding and explaining our world and how all things are connected. Cause and effect not only applies to mathematics, but to nature, life, and beyond.

While these definitions may seem very broad and philosophical, they are actually extremely simple and understanding what is cause and effect is a part of the human experience for every person.

If you are still a bit confused, looking at a few examples will make understanding cause and effect much easier for you. So, let’s go ahead and look at a simple example of a cause and effect relationship.

 

Photo by Alex Dukhanov on Unsplash

 

Example of Cause and Effect

Let’s start with a simple cause and effect example: after a rain storm, there are puddles on the street. In this example, we can consider the rain storm as a cause and the puddles as the effect.

In this case, the puddles forming were a result of the rain storm. If the rain storm never occurred, then the puddles would have never formed.

Examples like this should help you to understand that cause and effect relationships are extremely logical and they apply any situation or field of study concerned with patterns and outcomes.

Furthermore, cause and effect relationships help us to make sense of our world and make safe predictions about future events.

In the next section, we will take a deeper look at 5 unique cause and effect examples related to mathematics, history, nature, and daily life.

5 Cause and Effect Examples & Explanations

#1: Cause and Effect Examples: Learning How to Surf

The saying practice makes perfect is an application of a cause and effect relationship.

Whenever you are attempting to learn a new skill (how to surf in this example), the more time that you spend practicing, the better you become at the skill. This rule is true for learning any new skill, whether it be playing an instrument, speaking a new language, or riding a bike.

In the case of surfing, the amount of time a person spends practicing surfing is the cause and actually being able to surf is the effect. Without the cause (practicing), there would be no effect (knowing how to surf).

Another way of looking at this example is if someone who did not know how to surf hired an instructor and took a surfing classes. After several classes, the person learned how to surf. In this case, taking a surfing class would be the cause and being able to surf would be the effect.

Cause and Effect Example #1

A➔B: Taking surf lessons ➔ Being able to surf

Photo by Marvin Meyer on Unsplash

#2: Cause and Effect Examples: Weight Gain

According to the FDA, eating more calories than you burn leads to weight gain.

Whenever a person over-consumes calories without engaging in corresponding rigorous exercise, they can expect the result to be gaining body fat and an increase in body weight.

In this example, eating more calories than you burn is the cause and weight gain is the effect.

#3: Cause and Effect Examples: Deforestation and Climate Change

Cause and effect relationships also apply to nature and civilization.

For example, trees reduce the amount of greenhouse gases in our atmosphere.

Whenever forests are cut down (deforestation), greenhouse gases increase, which causes global warming and climate change.

So, in this example, the act of deforestation is the cause and global warming and climate change is the effect.

Cause and Effect Example #3

A➔B: Deforestation ➔ Global Warming

Photo by roya ann miller on Unsplash

#4: Cause and Effect Examples: Literature and Relationships

In this example, let’s take a look at how cause and effect plays a role in human relationships by examining Shakespeare’s Romeo and Juliet.

In the case of the classic tragedy, the ongoing feud between the Montague and Capulet families is the cause and the tragic deaths of Romeo and Juliet is the effect.

Why? Because the rivalry between the families is what led Romeo and Juliet to believe that they could never be together, thus spurring their decision to take their own lives.

#5: Cause and Effect Examples: Economics

In the case of economics, governments often argue for lowering taxes on businesses in an effort to boost economic growth and employment.

For example, a government may say that cutting taxes placed on businesses (the cause) will result in those businesses having more money on hand for investing. As a result, the government would expect a boost in employment and a spark in economic growth (effect).

Cause and Effect Example #5

A➔B: Lowering Taxes ➔ Economic Growth

Photo by Guilherme Cunha on Unsplash

Conclusion: Examples of Cause and Effect

No matter your current field of study, understanding cause and effect relationships is an extremely simple, yet powerful logic tool that will help you to make sense of basic and advanced concepts and ideas alike. By gaining a deep understanding of cause and effect relationships (which you can do by examining the cause and effect examples in this post), you will be better able to predict outcomes, think logically, solve complex problems, and make informed decisions.

In essence, every action has a reaction and there are consequences to our actions. And so, every action or event that is a cause has its corresponding action or event that is its effect. These simple concepts form the foundation of logical thinking and they will apply to all aspects of life.

Keep Learning

Who Invented Math? A Quick Explanation for Students

The history of math runs deep and spans across a variety of ancient cultures and civilizations, which leads many to wonder who invented math?

Let’s explore who gets the credit and why!

How Long Does It Take to Count to a Million?—Explained

How Long Does It Take to Count to a Million?—Explained

How Long Does It Take to Count to a Million?—Explained

How long would it take to count to a million and can it be done?

 

How long does it take to count to a million? (Image: Mashup Math via Getty)

 

So, you’re wondering how long would it take to count to a million. From a mathematical standpoint, the question itself seems simple enough. After all, you’re only interested in how much time it would take for the average person to actually count from one to one million. The answer must be some amount of time expressed in hours, days, or possibly even weeks or months.

And so our journey begins. To figure out how long it takes to count to a million, we will have to explore the number one million itself and perform a few calculations to see just how long it would take the average person to count to a million in both theoretical and practical scenarios.

This post explores two scenarios:

Are you ready to get started?

The Number One Million Explained

Before you learn just how long it takes to count to a million, it’s important that you have a solid understanding of the actual number and how relatively large it actually is. One of the best ways to grasp the magnitude of the number one million is to think of it as one thousand thousands.

In numeric form, this means that:

  • 1,000,000 = 1,000 x 1,000

So, counting to one million is the same thing as counting to 1,000 a thousand times! With this new perspective of a million in mind, it’s obvious that counting to a million is a pretty challenging task that would require a ton of time, effort, patience, and sheer will and dedication.

Now that you have a better understanding of how large a million actually is, you are ready to learn just how long it would take to reach this counting milestone.

 

How Long Does It Take to Count to a Million? To count to a million, you would have to count to a thousand a thousand times!

 

Theory : How Long to Count to a Million?

It’s finally time to perform some calculations to figure out how long it would theoretically take a person to count to a million.

We can start by considering the rate at which an average person can count and the total amount of numbers that will need to be counted (one million in this case).

Everyone counts numbers at different rates, but, for the sake of simplicity, let’s just assume that the average person can count one number per second. At this rate, it would take the person 1,000,000 seconds to count to a million.

But how long is 1,000,000 seconds? Well, to put this into perspective, one million seconds is approximately equivalent to 11 days, 13 hours, 46 minutes, and 40 seconds.

This means that, theoretically speaking, if a person were to count numbers at a rate of one number per second, it would require them to count for about 11.5 days straight without sleeping or taking any breaks!

Theoretically speaking, if a person were to count numbers at a rate of one number per second, it would require them to count for about 11.5 days straight without sleeping or taking any breaks!

While this answer to the question How Long Does It Take to Count to a Million? is true in theory, it is unrealistic in practice since it would be nearly impossible for a person to count non-stop all day and all night for nearly 12 consecutive days.

And it should be no surprise that a person has never counted from one to a million without stopping. But has a person ever counted to a million under more realistic conditions?

How long would it take to count to a million without stopping?

Reality : How Long to Count to a Million?

You now know that it would take nearly 12 days of non-stop counting to get from one to a million, which is a feat that is practically impossible for a human being to achieve.

In reality, a person can not count at a constant rate for days at a time since human beings, unlike computers, are subject to becoming tired, hungry, and fatigued.

However, this does not mean that a human being is not capable of counting to a million. It only means that getting there would take longer than 12 days since a human needs to take breaks from counting to eat, sleep, rest, etc.

While it is unknown how many people have counted to a million in their lifetimes, we do know of at least one person who has accomplished the feat—an American man named Jeremy Harper who holds the Guinness World Record for counting to a million.

Harper started counting on June 18, 2007 and reached a million on September 14, 2007. To achieve the milestone, Harper spent 16 hours per day counting and it took him a total of 89 days to complete the task! That means that the world record for counting to a million is nearly 3 months!

The feat was live-streamed daily from Harper’s home in Alabama. During his count, he never left his house or even shaved his face. His efforts raised over $10,000 USD for charity.

The world record for counting to a million is held by Jeremy Harper, who counted for 89 consecutive days for 16 hours a day.

 
 

Conclusion: How Long Does It Take to Count to a Million?

At this point, you should have a better appreciation for the magnitude of the number one million and the fact that counting to a million would take you at least 3 months to accomplish.

For the vast majority of people, counting to a million is probably not worth the time or energy, but exploring the question itself has hopefully been a fun and engaging experience.

And, if you ever again come across the question How long does it take to count to a million?, you will be equipped with a response that most will find surprising—the answer is that counting to a million would take you so long that it simply would not be worth attempting!

More Free Resources You Will Love:

Who Invented Math? A Quick Explanation for Students

The history of math runs deep and spans across a variety of ancient cultures and civilizations, which leads many to wonder who invented math?

Lets explore who gets the credit and why!