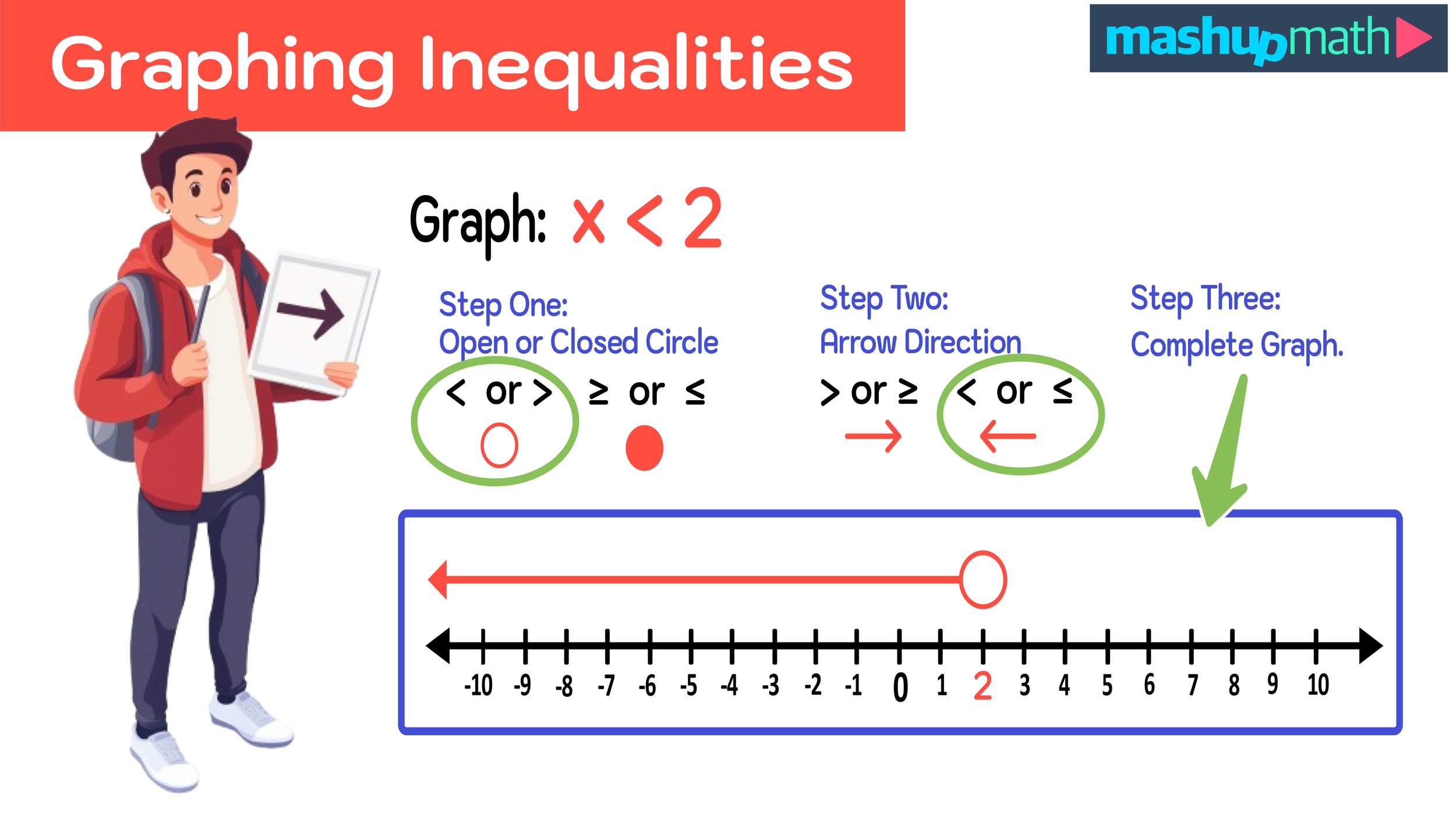
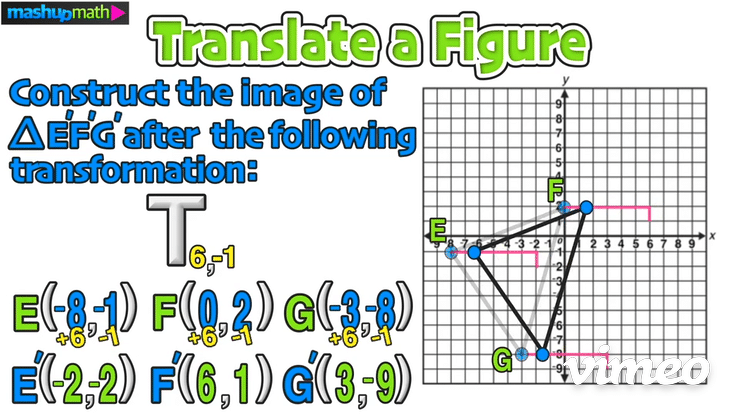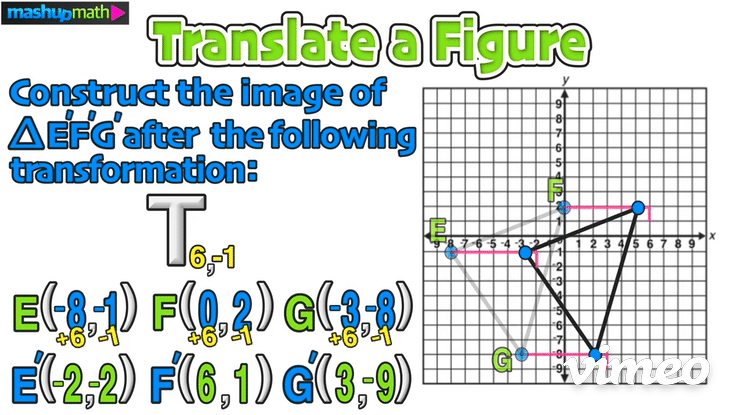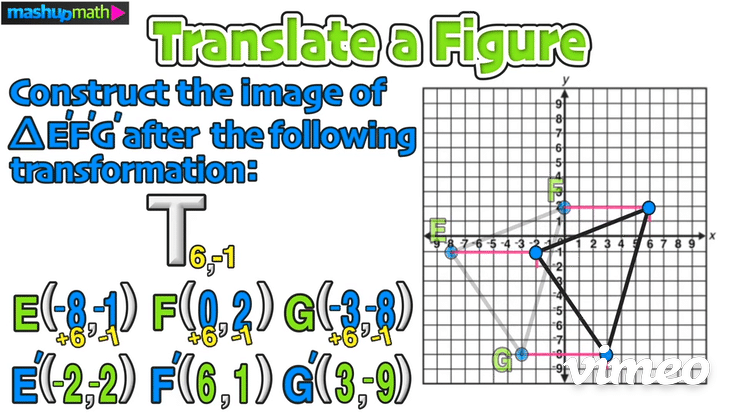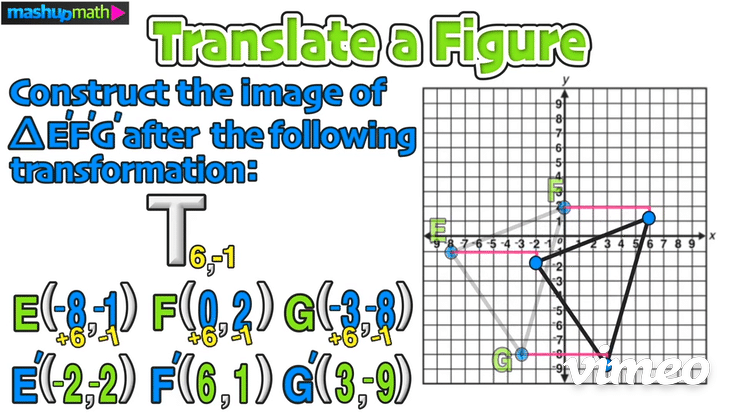
10 National Pi Day Fun Facts
March 14th is National Pi Day—a time to celebrate the mathematical π Symbol, which represents the value 3.1415926535897932384626433832…, but is often approximated to 3.14, which is why 3/14 is the date of National Pi Day every year.
You can celebrate at home and in the classroom by learning some awesome Pi Day fun facts that everyone should know!
Source: Mashup Math FP
Pi (π) represents the ratio of the circumference of any circle to its diameter. This groundbreaking mathematical fact is learned by all math students and is a fundamental math fact related to circles and cyclic relationships.
(Note that Pi Day should not be confused with Pi Approximation Day, which is celebrated on July 22nd since the fraction 22/7 is commonly used to approximate π since 22/7 = 3.142857143…)
There are many ways to celebrate National Pi Day, including snacking on circular-shaped foods like pizza and cookies, solving fun pi-themed math puzzles like the Which is More Pizza? brain teaser, and by learning some new fun facts about Pi and Pi Day.
For example, did you know that Albert Einstein’s birthday is on National Pi Day?
And if you want to learn more fun facts about Pi Day, check out our list of the 10 Most Interesting National Pi Day Fun Facts.
(Note that the following Pi Day Fun Facts are also featured on our 10 Pi Day Fun Facts YouTube video.
The Best National Pi Day Fun Facts
1.) The History of Pi Day
When was the first Pi Day?
The first National Pi Day was observed in 1988 by the American artist and physicist Larry Shaw in San Francisco by marching in circles with colleagues and snacking on different kinds of pie.
In 2009, the United States House of Representatives officially designated March 14th as National Pi Day and identified Shaw as the founder of the famous mathematical holiday.
Pi Day was first celebrated in San Francisco in 1988. (Photo by Daniel J. Schwarz on Unsplash)
2) What is π?
Pi (π) is the ratio of any circle’s circumference to its diameter.
The value of this ratio is approximately 3.14 and, yes, this relationship applies to any circle big or small.
3.) Where did the Pi Symbol (π) come from?
The π symbol that we use in math to represent pi was first used by the Swiss mathematician, physicist, and astronomer Leonard Euler in the year 1737.
Before Euler popularized using the Greek symbol π to represent the ratio of a circle’s circumference to its diameter, the value was known as Archimedes' constant.
Image: Creative Commons
Looking for more Pi Day activities?
Check out our super-popular Pi Day Fun Facts video on YouTube!
4.) How Long is Pi?
The value 3.14 is used as an approximation for Pi since it is an irrational number that continues on and on forever, hence the “…”
π =3.1415926535897932384626433832795028841971693…
The current world record for memorizing the digits of pi is 67,890 consecutive digits set by Lu Chao in 2005.
Mathematicians estimate that it would take 133 years for a person to recite the 6.4 billion known digits of Pi without stopping!
5.) What is the earliest reference to Pi?
Even though the Greek symbol π wasn’t adopted until the 1700s, the earliest references to the constant ratio between any circle’s circumference and diameter occurred in Ancient Egypt around 1650 BCE.
Pretty cool, right?
Pi dates back to Ancient Egypt! (Photo by Kévin et Laurianne Langlais on Unsplash)
6.) What is the most commonly occurring number in the first 100,000 decimal places of Pi?
The most common number in the first 100,000 decimal places of pi is the number 1, which occurs over 10,000 times!
Looking for more Pi Day activities?
Get your free Pi Day Fun Facts infographic!
(Perfect to share with students on March 14th!)
7.) Are there any famous Pi Day birthdays?
There are several famous people born on March 14th, Pi Day, including Albert Einstein, NBA All-Star Steph Curry, Actors Billy Crystal and Michael Caine, and Olympic Gold Medalist Simone Biles.
Image: Creative Commons
Image: Creative Commons
Image: Creative Commons
Source: Mashup Math MJ
8.) Who discovered the greatest number of digits of Pi?
Mathematician and computer scientist Fabrice Bellard calculated 2.7 trillion decimal places of pi using just a typical desktop computer in 2010.
That’s a lot of digits!
Looking for more Pi Day activities?
9.) How long is Pi?
As mentioned earlier, Pi is an irrational number and is thus infinite. In fact, it would take 12 billion digits of pi typed out using a normal-sized font to connect New York City and Kansas City.
And since pi goes on forever, it has enough digits to wrap around the entire world an infinite number of times!
Source: Mashup Math FP
10.) Is Pi present in nature?
You bet!
Pi can be used to measure circular natural events ranging from water ripples that emanate from a single point to finding the spherical volume of the entire universe (which can be done using only the first 39 digits of pi!)
Photo by Omar Gattis on Unsplash
11.) Bonus! What about Pie Day?
Even though Pi Day is a mathematical holiday, it’s hard to ignore the homophone that is PIE DAY.
Many people celebrate Pi Day by eating pie and other circular-shaped foods.
In fact, many pizzerias and bakeries offer special Pi Day deals and discounts on March 14th each year.
And as for pies, Apple Pie is considered the most preferred flavor of pie amongst Americans, with Pumpkin Pie coming in second, and Pecan Pie in third.
Photo by Hugo Aitken on Unsplash
(Never miss a Mashup Math blog--click here to get our weekly newsletter!)
By Anthony Persico