Kid Safe YouTube: A Safer Online Experience for Students

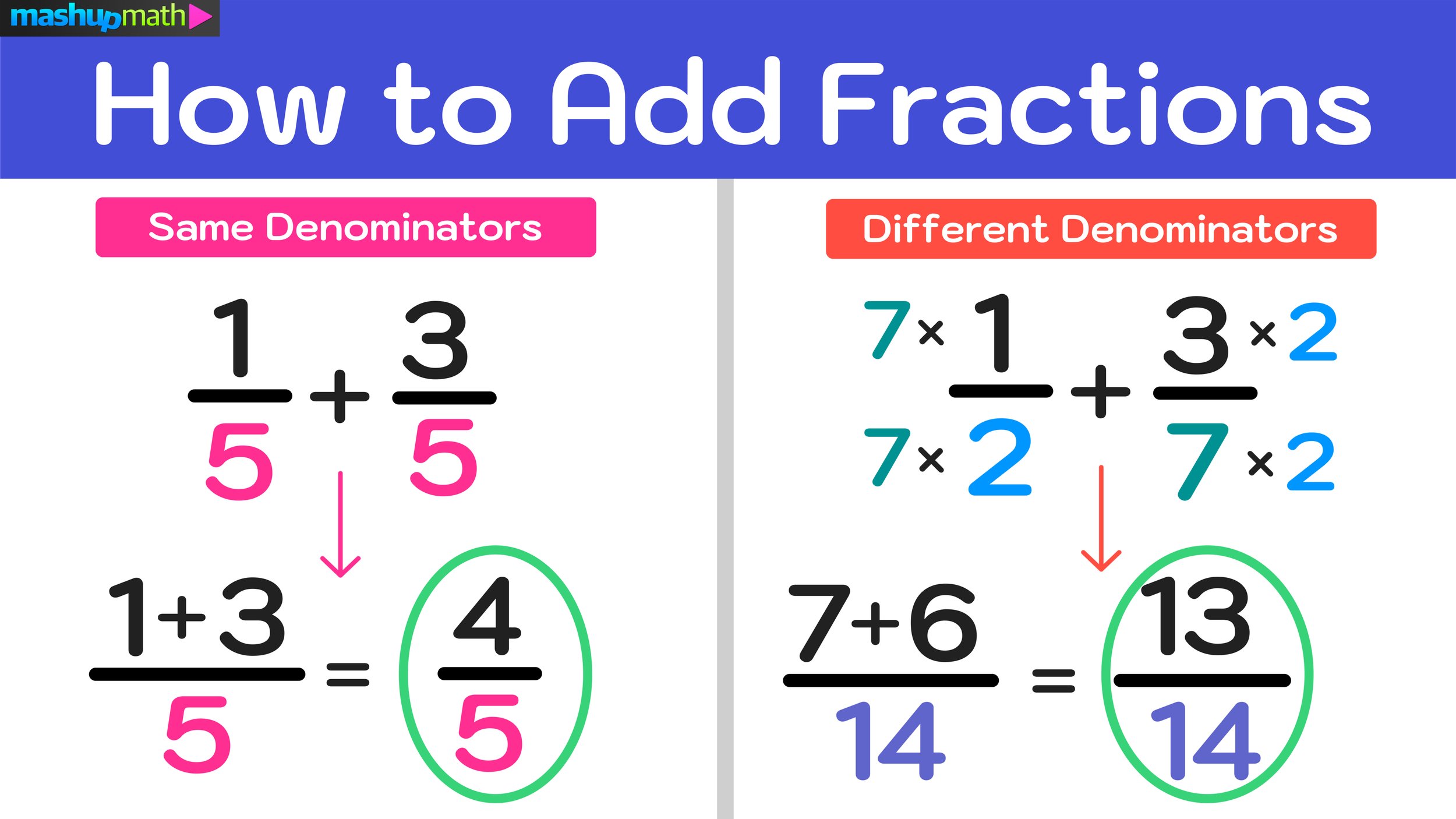
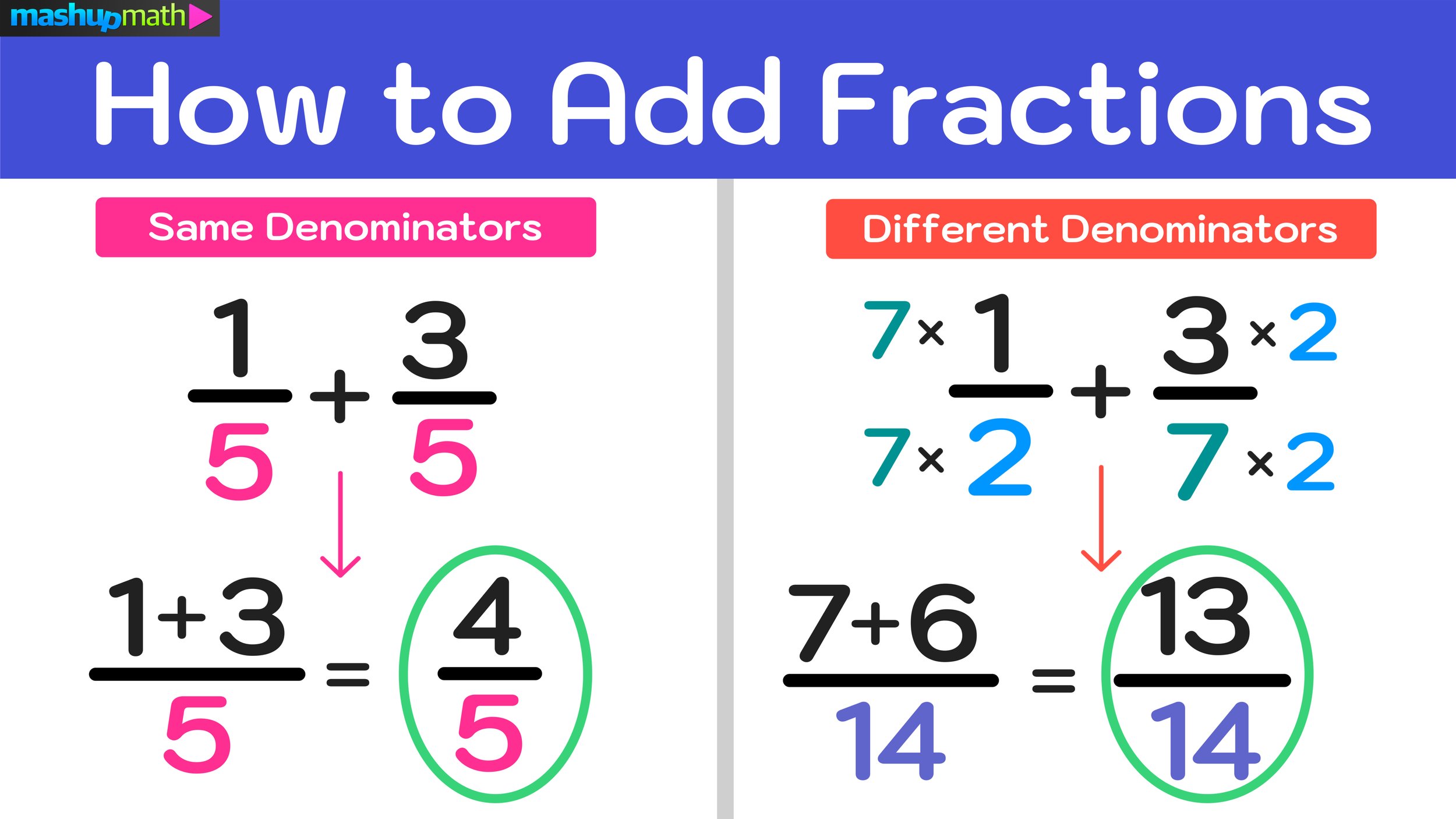
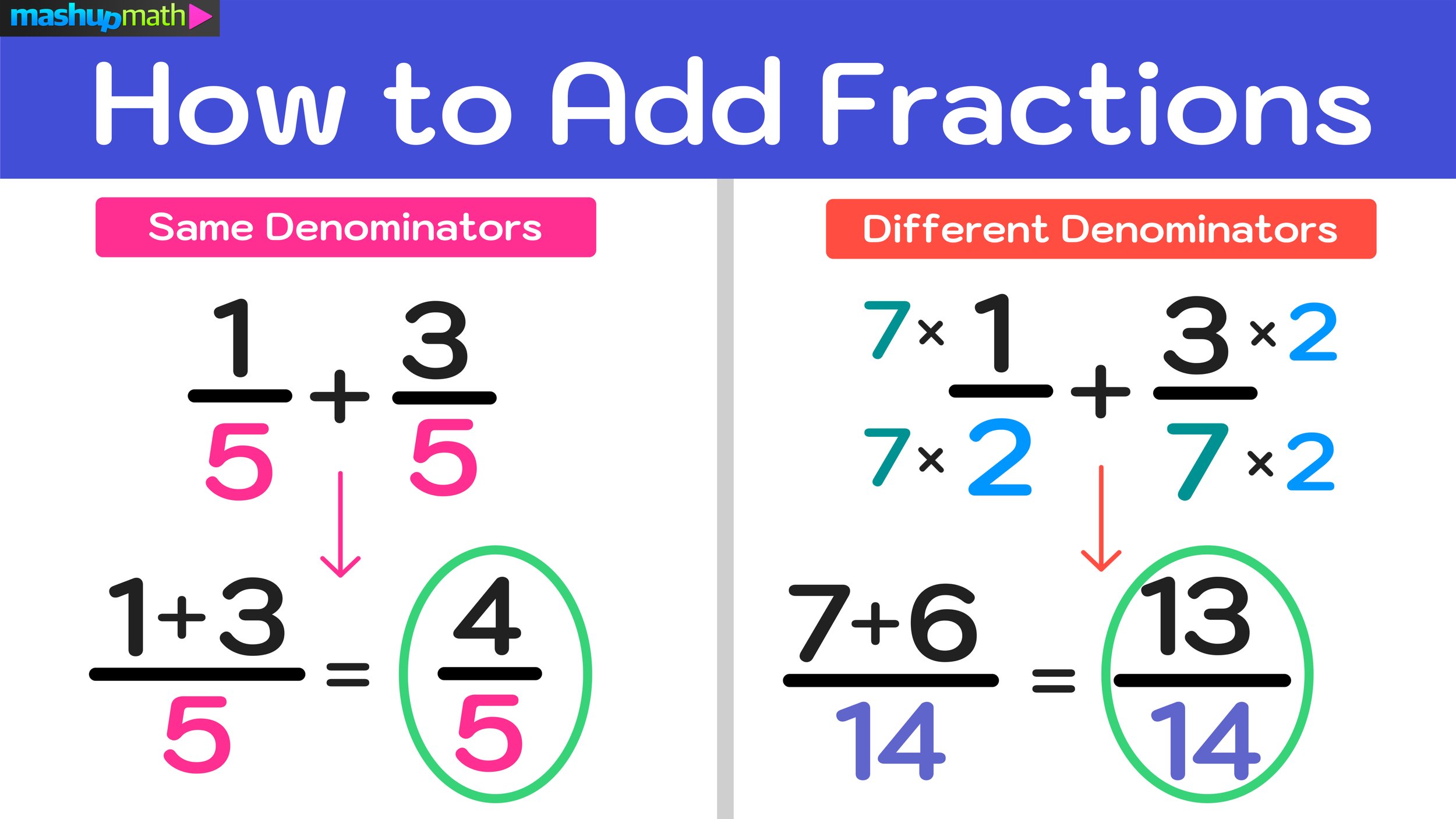
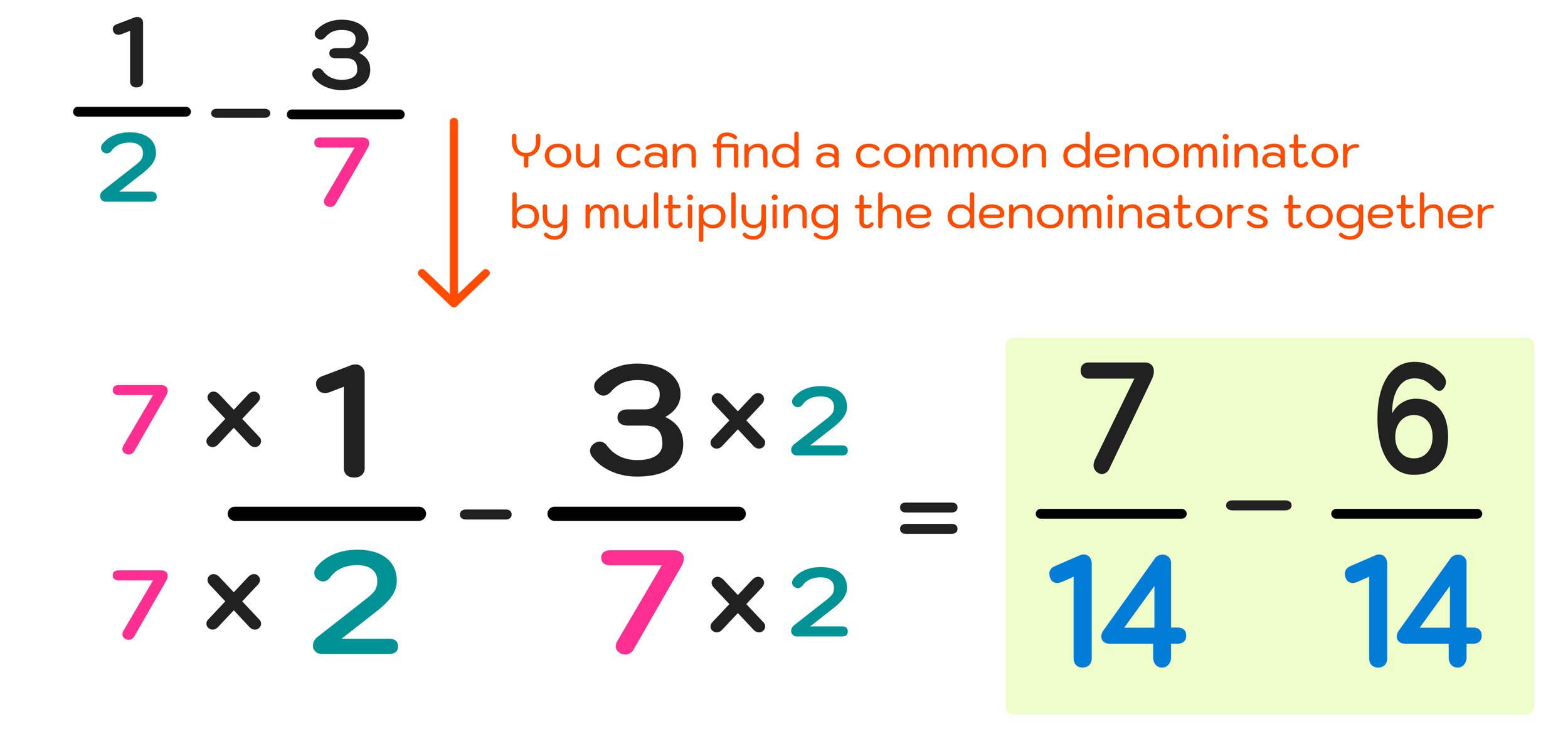How to Implement Kid Safe YouTube at Home and In Your Classroom

YouTube’s Kids Feature is a Safer and Simpler Version of the Platform that Allows Kids to Explore Their Interests by Watching Online Videos

Kid Safe YouTube is a specialized version of the YouTube platform that aims to provide a safe browsing and viewing experience for children. (Image: Mashup Math via Getty)

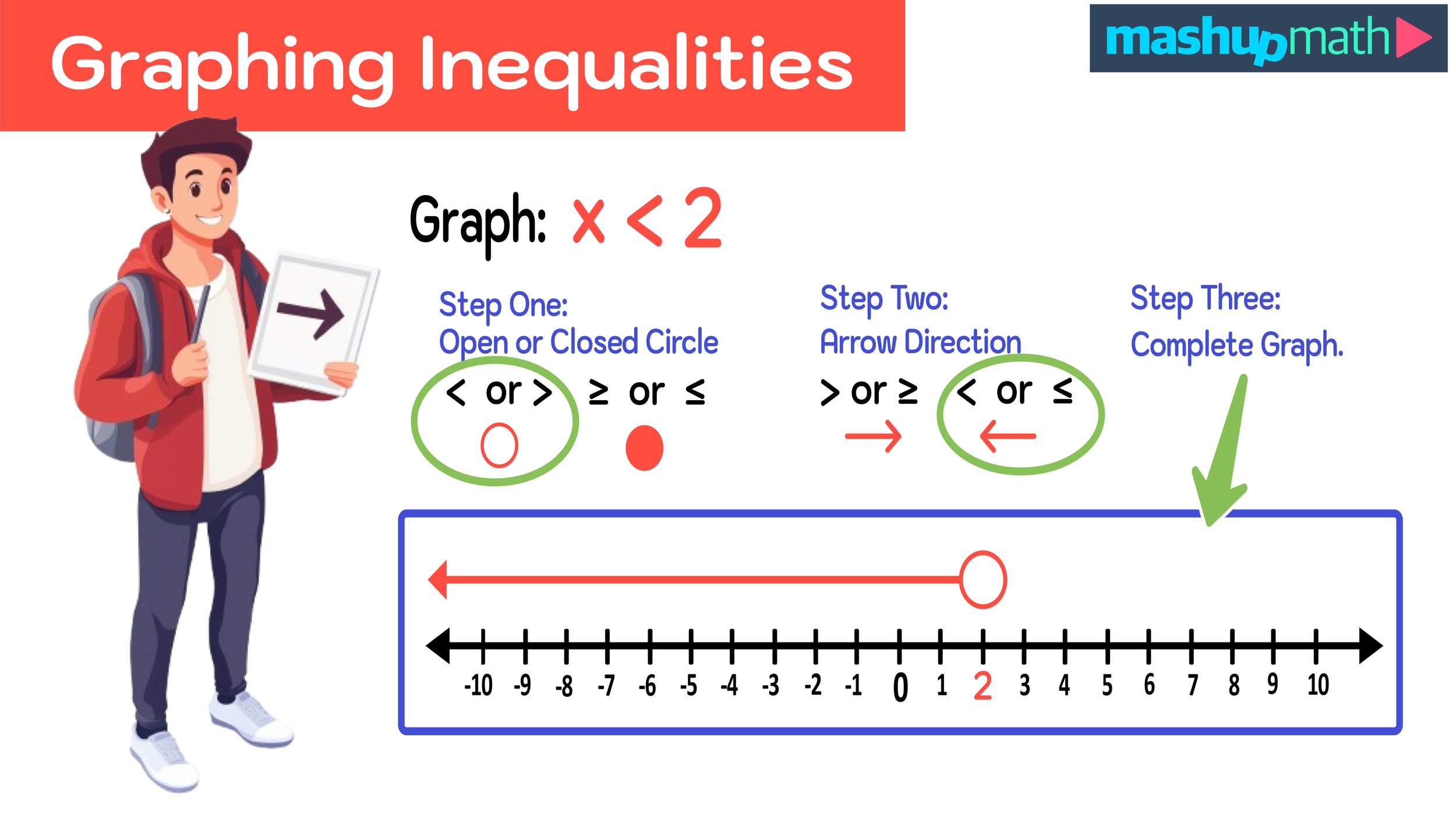
YouTube may be the single most powerful educational tool available to parents and teachers. The Google-owned search engine hosts a limitless collection of kid-friendly educational video content from respected outlets including Google Education, NASA, TED, and PBS.

But despite YouTube being host to the internet’s greatest collection of educational video content, many parents and school administrations are fearful of giving kids access to the platform given negative aspects including inappropriate content, advertisements, misinformation, cyberbullying, algorithm bias, and possibly dangerous interactions in the comment sections.

In fact, many school districts block student access to YouTube altogether, which prevents teachers from using YouTube videos or clips to supplement their lessons.

However, Google has recently unveiled a new specialized Kid Safe version of YouTube that removes the negative aspects of the platform and allows for a much safer online environment for children. In this post, we will dive into the following features of YouTube for Kids:

• What is Kid Safe YouTube?

• Is YouTube Kids safe?

• How can I get YouTube unblocked for school use?

• How can teachers use YouTube Kids in their classroom?

View fullsize

A screenshot of the YouTube Kids website. (Source: YouTube Kids)

Did You Know That There is a Kid-Safe YouTube?

While it is easy to understand why many teachers and parents do not want their kids to have access to YouTube given its negative aspects and potential for exposing kids to inappropriate content.

But, before you or your school gives up on the platform, you should know that Google has recently released a special Kid Safe YouTube version called YouTube Kids.

Kid Safe YouTube is a specialized version of the traditional YouTube platform that was designed to provide a safe browsing and viewing experience for kids by preventing their exposure to inappropriate or unsuitable content.

Some of the features of Kid Friendly YouTube that differentiate it from traditional YouTube include:

• All Kid Friendly YouTube videos must adhere to content policies and quality principles to ensure that they are appropriate and beneficial for kids.

• The Kid Friendly YouTube app has as a full suite of parental controls that will allow you to customize your child’s experience however you see fit.

• The App features a built-in timer feature that allows you to limit screen time.

• While the app does include limited paid advertisements, all ads must friendly and be in strict compliance with YouTube Kids' policies.

• The videos do not allow viewers to leave comments, so there is no comment section.

• Enhanced content filters and privacy settings.

YouTube Kids shares a free tutorial for setting up profiles for your kids so that you have control over things like screen time and what content they can access. (Source: YouTube Kids)

These range of features on Kid Safe YouTube are designed to protect children and allow them to experience and learn from YouTube content in a safe way.

By allowing parents and teachers to set filters and controls to limit the types of videos that kids can access on YouTube, the negative aspects of the platform can be removed, and students can gain the educational benefits of all the excellent learning content YouTube has to offer.

My School Blocks YouTube. How Can I Convince Them Not To?

Does your school block YouTube as a safety precaution?

If so, your district likely does not know about Kid Safe YouTube. By making this version of YouTube accessible to students, you can enjoy the pros of YouTube in your classroom without any of the cons.

This simple fix will open your classroom to hundreds of thousands of hours of amazing educational video content.

To learn more about YouTube Kids’ safety and security features, access FAQs, and learn how to setup the app in your home or school, click here to visit the YouTube Kids website.

Is YouTube Kids Safe? Yes! The app was designed to give kids a safer and more contained opportunity to explore video content. (Source: YouTube Kids)

Looking to Have YouTube Unblocked for School Use?

Is YouTube Kids Safe and is it Worth Implementing in Your Home or School?

Yes. Here are a few reasons to help convince you or your school’s administration that implementing Kid Safe YouTube is a great idea that will highly benefit students:

• YouTube is easily the most powerful online education tool available today—and it's free!

• Students are more engaged by video content than by verbal explanations alone.

• Students can create and share videos on YouTube to demonstrate their understanding of a topic.

• Any lesson can be supplemented with the inclusion of high-quality video content.

• Teachers can access a large library of Professional Development content.

• YouTube for schools is safe for the classroom and free and easy to implement.

Photo by charlesdeluvio on Unsplash

How Can Teachers Use Kid Safe YouTube in Their Classroom?

If you are a teacher or homeschool parent looking for ways to use YouTube videos in your classroom, here are a few examples:

• Educational Video Content: YouTube shares a massive selection of high-quality educational videos on all subjects and topics that teachers can use to supplement/enhance their instruction.

• Bring Concepts to Life: YouTube videos can be excellent for animated difficult concepts in fields such geometry, biology, and astronomy.

• Flipped Classroom: YouTube is a great platform for creating and sharing instructional videos that students can watch at home, which is a key component of the Flipped Classroom Model.

• Audio Features: YouTube is also an extremely useful tool for accessing audio content that can help students with things like learning a new language or studying the history of music.

• Projects: Teachers can also give their students opportunities to create and upload their own videos to complete a project or presentation—which allows them to be creative and learn digital skills such as video editing and graphic design.

While the traditional YouTube platform has tons of amazing educational content, its negative features led many parents and teachers to avoid using the platform, which is why Google has recently implemented YouTube Kids, which was designed to provide a safe and enjoyable environment for children to explore and learn about the world around them, without exposing them to any harmful or inappropriate content. So, if you want to reap all of the benefits of YouTube without any of the negative aspects of the traditional platform, then give YouTube kids a try today.

More Teaching Insights You Will Love:

Search Tags: YouTube Kids, kids youtube, youtube for kids, youtube kids app, kid youtube, youtube videos for kids, kid safe youtube, is youtube kids safe, kid-safe youtube, safe youtube for kids, how to make youtube safe for kids, is youtube safe for kids, youtube unblocked for school

Why Virtual Reality in Education Will Change Everything

Virtual Reality in Education

How Can VR Technology Transform the Way Students Learn?

Virtual Reality in Education (Image: Mashup Math via Getty)

The future is now.

Are you ready to take look into the role of virtual reality in education? In this post, we will dive into the exciting possibilities that VR technology can bring to your classroom.

Virtual Reality (VR) is a three-dimensional simulated experience that can be similar to or completely different from the real world. VR can be used to create and share an environment that is both immersive, interactive, and highly realistic.

As VR technology continues to become more mainstream, more and more students will be able to access new and exciting digital educational content.

What are the benefits of VR in education?

One of the most prominent benefits of virtual reality in education is that it can make learning more engaging, accessible, and interactive. By using VR technology, teachers can create a learning environment that is not only dynamic and interactive, but incredibly captivating and interesting.

And the applications of VR in education apply to all STEAM fields.

One of the most exciting applications of virtual reality in education is in science. In a virtual setting, students can explore complex scientific environments and concepts in a way that was previously impossible. For example, students can explore the inner workings of the human body, travel through the solar system, or even dive into the depths of the ocean to study marine life without ever having to leave the classroom.

For example, the free YouTube video below by Crash Course allows students to take a 360-degree tour of our universe and learn about each planet while floating in outer space.

Virtual Reality can also be incredibly useful for learning mathematics. VR can give students opportunities to visualize and interact with abstract concepts in ways that had previously not been possible. For example, students can explore geometrical shapes and figures in 3-dimensions, visualize and solve complex math equations, and even explore the behavior of mathematical functions in a way that is both interactive and engaging.

For example, the free YouTube video below by Mashup Math allows elementary math students to solve an order of operations math puzzle by finding clues within a 360-degree VR environment.

What’s Exciting About Virtual Reality Education?

One of the most exciting applications of VR in education is that the technology allows students to learn at their own pace. Using VR technology as a learning aide, students can explore and experiment with new concepts without the fear of failure. They can be experimental, take risks, and learn from their mistakes—all of which are desirable attributes of learning with a growth mindset.

Additionally, Virtual Reality can help students develop their critical thinking and problem-solving skills in a variety of ways. When using VR as a learning tool, students can explore complex scenarios and analyze the consequences of different actions. In the virtual environment, students are free to experiment with different approaches and see the results in real-time, allowing them to develop their analytical skills and think critically about complex problems.

There are tons of exciting applications for virtual reality in education.

Another exciting application of VR in education is that the technology can help students develop empathy and cultural understanding. Students can explore different cultures and perspectives using VR in a way that is both immersive and interactive. For example, they can explore different historical events, experience different lifestyles, and learn about different cultures in a way that is both engaging and informative.

Finally, VR can also be incredibly useful for students with disabilities or learning difficulties. With VR, students can access new learning opportunities that may be difficult or impossible to access in traditional classroom settings. For example, students with physical disabilities can explore and interact with virtual environments in a way that is not possible in the real world.

For example, this free YouTube video from VisitJapan allows students to explore Japanese architecture, cuisine, and cultural traditions.

VR in Education: Conclusion

Virtual Reality technology has the potential to revolutionize education and the way that students learn. By using VR to create and/or share immersive and interactive learning environments with their students, teachers can provide unique and truly engaging opportunities for developing critical thinking and problem-solving skills. Whether it's exploring complex scientific ideas or concepts, visualizing geometrical shapes, or experiencing a new geographic location or culture, VR has the potential to positively enhance education for learners of all ages and ability levels. While the role of VR in education is still in its infancy, the future is extremely exciting!

Keep Learning:

Nurturing a Growth Mindset for learning—where mistakes are celebrated as learning opportunities—is a key component of the STEAM Education movement. To learn more about how you can nurture a growth mindset in your classroom, check out our free Growth Mindset guide for teachers and parents.

---

More Education Resources You Will Love:

Search Tags: virtual reality in education, virtual reality education, virtual reality for education, benefits of virtual reality in education, virtual reality and education, vr in education, benefits of vr in education, education in VR

How to Subtract Fractions in 3 Easy Steps

How to Subtract Fractions in 3 Easy Steps

Math Skills: How do you subtract fractions with the same denominator and how to subtract fractions with different denominators

Free Step-by-Step Guide: How do you subtract fractions?

Having the knowledge of how to subtract fractions is a crucial and fundamental math skill that every student must learn, as it serves as a foundational element for comprehending more advanced math ideas that you may come across in the future.

(Looking to learn how to add fractions? Click here to access our free guide)

Fortunately, subtracting fractions, regardless of whether the denominators are the same (like) or different (unlike) can be done using a straightforward and uncomplicated three-step process.

This free Step-by-Step Guide on How to Subtract Fractions will walk you through the process of subtracting fractions with like and unlike denominators, including detailed examples for each scenario.

This step-by-step guide will focus on teaching you the following math skills:

• How to subtract fractions with the same denominator?

• Subtracting Fractions with Unlike Denominators: How to subtract fractions with different denominators?

Before we cover how to subtract fractions and work through a few examples, let’s do a fast recap of some key characteristics and vocabulary terms related to subtracting fractions.

Let’s get started!

Subtracting Fractions: Definitions and Vocabulary

Before you can learn how to subtract fractions, it’s important for you to know two key vocabulary terms (and the difference between them):

Definition: The top number of a fraction is called a numerator. For example, the fraction 5/6 has a numerator of 5.

Definition: The bottom number of a fraction is called a denominator. For example, the fraction 5/6 has a denominator of 6.

Again, the numerator is the top number of a fraction, and the denominator is the bottom number. These terms are further illustrated in Figure 01 below. While these two math vocabulary terms are simple, it is crucial that you are able to understand and correctly identify the numerator and denominator of fractions in order to master the skill of subtracting fractions.

Figure 01: Fraction Subtraction Key Terms: The numerator of a fraction is the top number, and the denominator is the bottom number.

Moving on, you are ready to take the next step towards mastering fraction subtraction. Next, you will need to be able to determine when a fraction subtraction problem falls into one of the following two categories:

• Subtracting Fractions with Like Denominator (the denominators equal the same number)

• Subtracting Fractions with Unlike Denominator (the denominators are different)

Fractions that have like denominators have bottom numbers that equal the same value.

• Example: 3/5 - 1/5 → This would be a case of subtracting fractions with like denominators since both fractions have a denominator of 5.

Alternatively, fractions that have unlike denominators have bottom numbers that do not equal the same value.

• Example: 1/2 - 3/7 →This would be a case of subtracting fractions with unlike denominators since both fractions have different bottom numbers (one has a denominator of 2 and the other has a denominator of 7).

Both examples (one with like denominators and one with unlike denominators) are illustrated in Figure 02 below.

Figure 02: How do you subtract fractions? The first step is being able to identify whether the fractions in question have like denominators or unlike denominators.

This concept may seem uncomplicated, but it is essential to refresh your understanding since you must be able to recognize if a problem involving subtracting fractions has like or unlike denominators in order to find a correct solution.

Now that you have the important foundation skills, you are ready to work through a few fraction subtraction problems.

---

How to Subtract Fractions with Like Denominators

How to Subtract Fractions with Like Denominators: Example #1

Example #1: 3/5 - 2/5

The first fraction subtraction example is pretty easy and straightforward, which is why it is a good place to start using our simple 3-step process for subtracting fractions. If you can learn to apply these three steps to easy examples, then you will be able to use the same process to solve more complex problems in the future (since the process works for any fraction subtraction problem).

How Do You Subtract Fractions in 3 Easy Steps?

• Step One: Identify whether the denominators are the same (like) or different (unlike).

• Step Two: If the example involves like denominators, move onto Step Three. If they are unlike denominators, find a common denominator.

• Step Three: Subtract the numerators and find the difference.

Now that you know the steps, let’s apply them to solving this first example:

• 3/5 - 1/5 = ?

Step One: Identify whether the denominators are the same (like) or different (unlike).

The fractions in this example have like denominators. They are both 5.

Step Two: If the example involves like denominators, move onto Step Three. If they are unlike denominators, find a common denominator.

Since the denominators are the same, you can skip ahead to the next step.

Step Three: Subtract the numerators and find the difference.

To complete this fraction subtraction problem, simply subtract the numerators and express the result as follows:

• 3/5 - 1/5 = (3-1)/5 = 2/5

Since 1/5 can not be reduced, you can conclude…

Final Answer: 2/5

Figure 03 below illustrates how you came to this conclusion.

Figure 03: How to Subtract Fractions with Like Denominators: Subtract the numerators and keep the denominator.

The first example shows you that subtracting fractions with like denominators is pretty easy.

To subtract fractions with the same denominator, subtract the numerators and keep the same denominator.

Now, let’s move onto one more example of subtracting fractions with like denominators before moving onto examples of how to subtract fractions with different denominators.

---

How to Subtract Fractions with Like Denominators: Example #2

Example #2: 8/9 - 5/9

For the next example, you will be applying the same 3-step method that you used in Example #1 as follows:

Step One: Identify whether the denominators are the same (like) or different (unlike).

In this example, the fractions have like denominators. They are both 9.

Step Two: If the example involves like denominators, move onto Step Three. If they are unlike denominators, find a common denominator.

Again, since the denominators are the same, you can skip ahead to Step Three.

Step Three: Subtract the numerators and find the difference.

To complete this fraction subtraction problem, subtract the numerators as follows:

• 8/9 - 5/9 = (8-5)/9 = 3/9

In this case, 3/9 is the correct answer, but this fraction can be simplified. Since both 3 and 9 are divisible by 3, 3/9 can be simplified as 1/3.

Final Answer: 1/3

Figure 04 below illustrates how you just solved Example #2.

Figure 04: Subtracting Fractions: 3/9 can be simplified to 1/3

Now, let’s move onto learning how to subtract fractions with different denominators.

---

How to Subtract Fractions with Different Denominators

How to Subtract Fractions with Different Denominators: Example #1

Example #1: 1/2 - 3/7

Step One: Identify whether the denominators are the same (like) or different (unlike).

In this example, the fractions have unlike denominators (they are different). The first fraction’s denominator is 2 and the other’s is 7.

Step Two: If the example involves like denominators, move onto Step Three. If they are unlike denominators, find a common denominator.

Since the fractions have unlike denominators, you can not skip ahead.

Before you can move onto Step Three, you have to find a number that both denominators can divide into evenly. This is called a common denominator.

A very easy and effective way to find a common denominator between two fractions is by multiplying the denominators together (i.e. multiplying the denominator of the first fraction by the second fraction and multiplying the denominator of the second fraction by the first fraction.

• 1/2 - 3/7 (1x7)/(2x7) - (3x2)/(7x2) = 7/14 - 6/14

This fraction subtraction process is illustrated in Figure 05 below.

Figure 05: How to Subtract Fractions with Different Denominators: Find a common denominator by multiplying the denominators together.

(Looking for some extra help with multiplying fractions, click here to access our free student guide).

Now that Step Two is complete, you can see that the original question has been transformed and you are now working with equivalent fractions that have common denominators, which means that the heavy lifting has been done and you can now solve the problem by subtracting the numerators and keep the same denominator:

• 7/14 - 6/14 = (7-6)/14 = 1/14

Since 1/14 can not be reduced further, you have solved the problem…

Final Answer: 1/14

Figure 06: Once you have common denominators, simply subtract the numerators keep the same denominator.

Are you ready for one more practice problem for how to subtract fractions with unlike denominators?

---

How to Subtract Fractions with Different Denominators: Example #2

Example #1: 2/3 - 8/15

For this final example of subtracting fractions, you will again be using the 3-step method as follows:

Step One: Identify whether the denominators are the same (like) or different (unlike).

The fractions have unlike denominators (one is 3 and the other is 5).

Step Two: If the example involves like denominators, move onto Step Three. If they are unlike denominators, find a common denominator.

Just like last example, you will have to find a common denominator since the fractions have unlike denominators. You can find a common denominator by multiplying the denominators together as follows:

• (2x15)/(3x15) - (8x3)/(15x3) = 30/45 - 24/45

This process is shown in Figure 07 below.

Figure 07: How to Subtract Fractions with Different Denominators

Now that the fractions share a common denominator, you can solve the fraction subtraction problem as follows:

• 30/45 - 24/45 = (30-24)/45 = 6/45

Since both 6 and 45 are divisible by 3, you can simplify this fraction as…

Final Answer: 2/15

Figure 08: Subtracting Fractions with Unlike Denominators

Conclusion: How to Subtract Fractions

Subtracting fractions with like denominators involves simply finding the difference of the numerators (top values) and not changing the denominator (bottom value).

Subtracting fractions with unlike denominators requires you to find a common denominator, which is a value that both denominators divide evenly into.

How do you subtract fractions? You can solve any fraction subtraction problem by applying the following three step method:

• Step One: Identify whether the denominators are the same (like) or different (unlike).

• Step Two: If the example involves like denominators, move onto Step Three. If they are unlike denominators, find a common denominator.

• Step Three: Subtract the numerators and find the difference.

Keep Learning:

How to Add Fractions in 3 Easy Steps

---

Search Tags: how to subtract fractions, subtracting fractions, how to subtract fractions with different denominators, fraction subtraction, subtracting fractions with unlike denominators, how do you subtract fractions?

How to Add Fractions in 3 Easy Steps

How to Add Fractions in 3 Easy Steps

Math Skills: How to add fractions with the same denominator and how to add fractions with different denominators

Knowing how to add fractions is an important and fundamental math skill.

Since fractions are a critically important math topic, understanding how to add fractions is a fundamental building block for mastering more complex math concepts that you will encounter in the future.

(Looking to learn how to subtract fractions? Click here to access our free guide)

Luckily, learning how to add fractions with like and unlike (different) denominators is a relatively simple process. The free How to Add Fractions Step-by-Step Guide will teach you how to add fractions when the denominators are the same and how to add fractions with different denominators using a simple and easy 3-step process.

This guide will teach you the following skills (examples included):

• What is the difference between the numerator and denominator of a fraction?

• How to add fractions with the same denominator?

• How to add fractions with different denominators?

But, before you learn how to add fractions, let’s do a quick review of some key characteristics and vocabulary terms related to fractions before we move onto a few step-by-step examples of how to add fractions.

Are you ready to get started?

How to Add Fractions: Definitions and Vocabulary

In order to learn how to add fractions, it is imperative that you understand the difference between a numerator and a denominator.

Definition: The numerator of a fraction is the top number in the fraction. For example, in the fraction 3/4, the numerator is 3.

Definition: The denominator of a fraction is the bottom number in the fraction. For example, in the fraction 3/4, the denominator is 4.

Pretty simple, right? These terms are visually represented in Figure 01 below. Make sure that you understand the difference between the numerator and the denominator of a fraction before moving forward in this guide. If you mix them up, you will not learn how to add fractions correctly.

Figure 01: The numerator is the top number of a fraction, and the denominator is the bottom number of a fraction.

Now that you know the difference between the numerator and the denominator of a fraction, you are ready to learn how to identify whether or not a given problem involving adding fractions falls into which of the following categories:

• Like Denominators (the denominators are the same)

• Unlike Denominators (the denominators are different)

Fractions with like denominators have bottom numbers that equal the same value. For example, in the case of 1/5 + 3/5, you would be adding fractions with like denominators since both fractions have a bottom number of 5.

Conversely, fractions with different (or unlike) denominators have bottom numbers that do not equal the same value. For example, in the case of 1/2 + 3/7, you would be adding fractions with different denominators since the fractions do not share a common denominator (one has a denominator of 2 and the other has a denominator of 7).

These examples are featured in Figure 02 below.

Figure 02: In order to learn how to add fractions, you must be able to identify when the fractions have denominators that are the same and when they have different denominators.

Again, this concept should be simple, but a quick review was required because you will need to be able to identify whether or not a fractions addition problem involves like or unlike denominators in order to solve it correctly.

Now, let’s move onto a few examples.

---

How to Add Fractions with Like Denominators

How to Add Fractions with Like Denominators: Example #1

Example #1: 1/4 + 2/4

Our first example is rather simple, but it is perfect for learning how to use our easy 3-step process, which you can use to solve any problem that involves adding fractions:

• Step One: Identify whether the denominators are the same or different.

• Step Two: If they are the same, move onto Step Three. If they are different, find a common denominator.

• Step Three: Add the numerators and find the sum.

Okay, let’s take our first attempt at using these steps to solve the first example: 1/4 + 2/4 = ?

Step One: Identify whether the denominators are the same or different.

Clearly, the denominators are the same since they both equal 4.

Step Two: If they are the same, move onto Step Three. If they are different, find a common denominator.

Since the denominators are the same, you can move onto Step Three.

Step Three: Add the numerators and find the sum.

To complete this first example, simply add the numerators together and express the result as one single fraction with the same denominator as follows:

• 1/4 + 2/4 = (1+2)/4 = 3/4

Since 3/4 can not be simplified further, you can conclude that…

Final Answer: 3/4

This process is summarized in Figure 03 below.

Figure 03: How to Add Fractions: The process is relatively simple when the denominators are the same.

As you can see from this first example, learning how to add fractions when the denominators are the same is very simple.

To add fractions with the same denominator, simply add the numerators and keep the same denominator.

Let’s take a look at one more example of adding fractions when the denominators are the same before you learn how to add fractions with different denominators.

---

How to Add Fractions with Like Denominators: Example #2

Example #2: 2/9 + 4/9

To solve this second example, let’s apply the 3-step process like we did in the previous example as follows:

Step One: Identify whether the denominators are the same or different.

The denominators in this example are the same since they both equal 9.

Step Two: If they are the same, move onto Step Three. If they are different, find a common denominator.

Again, you can skip the second step because the denominators are the same.

Step Three: Add the numerators and find the sum.

The final step is to add the numerators and keep the denominator the same:

• 2/9 + 4/9 = (2+4)/9 = 6/9

In this case, 6/9 is the correct answer, but this fraction can actually be reduced. Since both 6 and 9 are divisible by 3, 6/9 can be reduced to 2/3.

Final Answer: 2/3

This process is summarized in Figure 04 below.

Figure 04: How to Add Fractions: 6/9 can be reduced to 2/3

Next, let’s learn how to add fractions with different denominators.

---

How to Add Fractions with Different Denominators

How to Add Fractions with Different Denominators: Example #1

Example #1: 1/3 + 1/4

Step One: Identify whether the denominators are the same or different.

In this case, the denominators are different (one is 3 and the other is 4)

Step Two: If they are the same, move onto Step Three. If they are different, find a common denominator.

For this example, you can not skip the second step. Before you can continue on, you will need to find a common denominator—a number that both denominators can divide into evenly.

The easier way to do this is to multiply the denominator of the first fraction by the second fraction and the denominator of the second fraction by the first fraction (i.e. multiply the denominators together).

• 1/3 + 1/4 (4x1)/(4x3) + (3x1)/(3x4) = 4/12 + 3/12

This process is shown in Figure 05 below.

Figure 05: How to Add Fractions with Different Denominators: Get a common denominator by multiplying the denominators together.

(If you need some help with multiplying fractions, click here to access our free guide).

Now, we have transformed the original question into a scenario involving adding two fractions that do have common denominators, which means that the hard work is over and we can solve by adding the numerators and keep the same denominator:

• 4/12 + 3/12 = (4+3)/12 = 7/12

Since 7/12 can not be simplified further, you can conclude that…

Final Answer: 7/12

Figure 06: Once you have common denominators, you can simply add the numerators together and keep the same denominator.

Now, let’s work through one final example of adding fractions with unlike denominators.

---

How to Add Fractions with Different Denominators: Example #2

Example #1: 3/5 + 4/11

For this last example, let’s again apply the 3-step process:

Step One: Identify whether the denominators are the same or different.

The denominators are clearly different (one is 5 and the other is 11)

Step Two: If they are the same, move onto Step Three. If they are different, find a common denominator.

Just like the last example, the second step is to find a common denominator by multiplying the denominators together as follows:

• 3/5 + 4/11 (11x3)/(11x5) + (5x4)/(5x11) = 33/55 + 20/55 = 53/55

This process is shown in Figure 07 below.

Figure 07: How to Add Fractions with Different Denominators: Get a common denominator by multiplying the denominators together.

Finally, now that you have common denominators, you can solve the problem as follows:

• 33/55 + 20/55 = (33+20)/55 = 53/55

Since there is no value that divides evenly into both 53 and 55, you can not simplify the fraction further.

Final Answer: 53/55

Figure 08: How to Add Fractions with Different Denominators: 53/55 can not be simplified further.

Conclusion: How to Add Fractions

To add fractions with the same denominator, simply add the numerators (top values) and keep the same denominator (bottom value).

To add fractions with different denominators, you need to find a common denominator. A common denominator is a number that both denominators can divide into evenly.

You can solve problems involving adding fractions for either scenario by applying the following 3-step process:

• Step One: Identify whether the denominators are the same or different.

• Step Two: If they are the same, move onto Step Three. If they are different, find a common denominator.

• Step Three: Add the numerators and find the sum.

Keep Learning:

How to Subtract Fractions in 3 Easy Steps

---

Search Tags: how to add fractions, how to add fractions with different denominators, how to add fraction , how to add fractions with unlike denominators, how to. add fractions, how to add fractions with, how to add a fraction

Who Invented Math?—Explanation for Students

Who Invented Math?

A Quick Explanation of the History of Math for Students

Who invented math? Not Pythagoras, but his contributions to the field of mathematics are alive and well today.

The history of math runs deep and spans across a variety of ancient cultures and civilizations, which leads many to wonder who invented math?

Some people might think that mathematics just magically appeared out of thin air as if it were discovered in a dream, and many do believe that mathematics was somehow discovered rather than invented.

Either way, mathematics has not always been as broad and well understood as it is today. In fact, the field of mathematics has been evolving and growing over thousands of years, with contributions from various cultures and individuals.

Let's start our exploration of the question “who invented math?” with the ancient Babylonians, who developed a number system based on 60. This system is still used today in time and angle measurements, which is an absolutely extraordinary fact considering that the Babylonian number system dates back to approximately 1800 B.C. They were also skilled at solving quadratic equations, and they even had a form of algebraic notation. Since you can’t do math without numbers, the Babylonians deserve a lot of credit for laying the groundwork for modern day mathematics.

Who invented math? The ancient Babylonians developed one of the first number systems, but do they deserve all of the credit? (Image: Mashup Math FP)

But who invented math? The Babylonians developed one of the first instances of numbers, but do they get the full credit?

Our next stop along the timeline of the history of math takes us to ancient Egypt. The ancient Egyptians had a great need for mathematics in order to build their pyramids and engineer their complex society, and they developed a system of mathematics that relied heavily on geometry. They were extremely talented at calculating areas and volumes, and they even had a formula for finding the volume of a truncated pyramid.

Who invented math? The ancient Egyptians made tremendous contributions to all fields of mathematics including geometry. (Image: Mashup Math FP)

The ancient Egyptians made some unbelievable contributions to the field of mathematics, but it would be hard to say that they should get all of the credit for inventing math. But who could top the Egyptians?

Enter the ancient Greeks. These folks were absolute legends when it came to contributions in the field of mathematics. Of course, there was Plato, whose study of mathematics led him to classify the Platonic Solids as the building blocks of the universe. But the ancient Greeks also produced some of the greatest mathematical minds of all time, including Pythagoras, Euclid, and Archimedes.

Pythagoras, of course, is known for the Pythagorean Theorem, which is still used today to find the length of the sides of a right triangle. Euclid, on the other hand, is known for his work in geometry, and he wrote a book called "Elements" that is still used today as a textbook in many math classes. And Archimedes? This guy was a true mathematical genius. He made huge contributions to geometry and calculus, and he even developed a system for calculating the volume of irregularly shaped objects.

Who invented math? Any discussion of the history of math must include the ancient Greeks. (Image: Mashup Math FP)

So, who invented math? Not exactly the Greeks, but they deserve tons of credit for advancing the field to entirely new levels.

While the roots of math all stem from ancient civilizations, the history of math continues well beyond ancient times.

Fast forward to the 17th century, and we have the one and only Sir Isaac Newton. Arguably the most famous and influential mathematician of all time, Newton was a true math and science pioneer, and he's responsible for developing the field of calculus. He also made huge contributions to physics and astronomy, so he's basically a superhero in the world of math and science.

Who invented math? Not Sir Isaac Newton—but he is viewed by many as the most influential mathematician of all time. (Image: Mashup Math via Getty)

And let's not forget about another 17th century math legend: Gottfried Leibniz. He also independently developed calculus, which was pretty impressive considering he and Newton were working on opposite sides of Europe at the time. Leibniz was also a philosopher, and he made important contributions to the study of the concept of infinity.

And while this tour through the history of math has so far featured only male mathematicians, there have been tons of incredible contributions made to the field of mathematics by famous women mathematicians like Sophie Germain, Emmy Noether, Katherine Johnson, and Valerie Thomas.

Who invented math? Not Valerie Thomas, but she did use math to invent the illusion transmitter—a 3D imaging technology that was the first of its kind when it was first put into use by NASA in 1980. (Image: Wikipedia Commons)

In addition to famous women mathematicians, the history of math is filled with contributions made by often overlooked African American mathematicians like Fern Hunt, Mark Dean, and Lonnie Johnson, all of whom played a significant role in the progression of the field.

So, now that you have a better idea of the history of math and how it has developed over thousands of years, can you confidently state who invented math?

The answer should be no. Why? Because mathematics has been around for nearly as long as humanity has had a presence on Earth, and it has evolved by leaps and bounds over thousands of years.

History of Math: Math was discovered and developed by many different cultures and individuals throughout history. (Image: Mashup Math FP)

The only way to answer the question “who invented math?“ is to say that math was discovered and developed by many different cultures and individuals throughout history. From the Babylonians to the Greeks to Newton and Leibniz, math has been molded and shaped by countless brilliant minds over the centuries.

In conclusion, mathematics is beautiful and complex field of study, and we owe many men and women gratitude and respect for its development and progression. So, the next time you're struggling through a math problem, just remember that you're a part of a long history of individuals who have been using and refining mathematics for thousands and thousands of years.

Do you want more insights from great mathematicians from history? Click here to see of collection of the 37 Greatest Math Quotes of All Time

---

More Math Resources You Will Love: