What is a Whole Number in Math?

What is a Whole Number in Math?

What is a Whole Number in Math?

What is a whole number in math, is 0 a whole number, and how can you tell if a number is a whole number or not?

 

What is a whole number in math?

 

Do you remember when you first started learning how to count? At this early stage, you likely used your fingers as a simple counting tool. One, two, three, four, and so on. While the days of counting on your fingers are likely long behind you, the journey that you began then has led you to this point, where you are ready to learn about whole numbers, what they are, and how they fit into the number system.

Before we dive into learning about whole numbers, lets quickly review the definition of a natural number so that you can understand the difference between a natural number and a whole number later on.

What is a Natural Number?

In math, natural numbers are the numbers that we use for counting and ordering values or amounts. The set of natural numbers starts at 1 and is as follows: { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, …}

Natural numbers are sometimes referred to as counting numbers. Notice that the set of natural numbers does not include 0, fractions/decimals, or negative numbers.

We can visualize the natural numbers on a number line as shown in Figure 01 below:

 

Figure 01: What is a Natural Number?

 

What is a Whole Number?

Now that you know what a natural number is, you can extend that understanding to whole numbers.

In math, whole numbers are a set of numbers that includes all of the natural numbers as well as 0.

The set of whole numbers starts at 0 and is as follows: { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, …}

Notice that, just like the set of natural numbers, the set of whole numbers does not include fractions/decimals or negative numbers.

We can visualize the whole numbers compared to the natural numbers on a number line as shown in Figure 02 below:

 

Figure 02: What is a whole number?

 

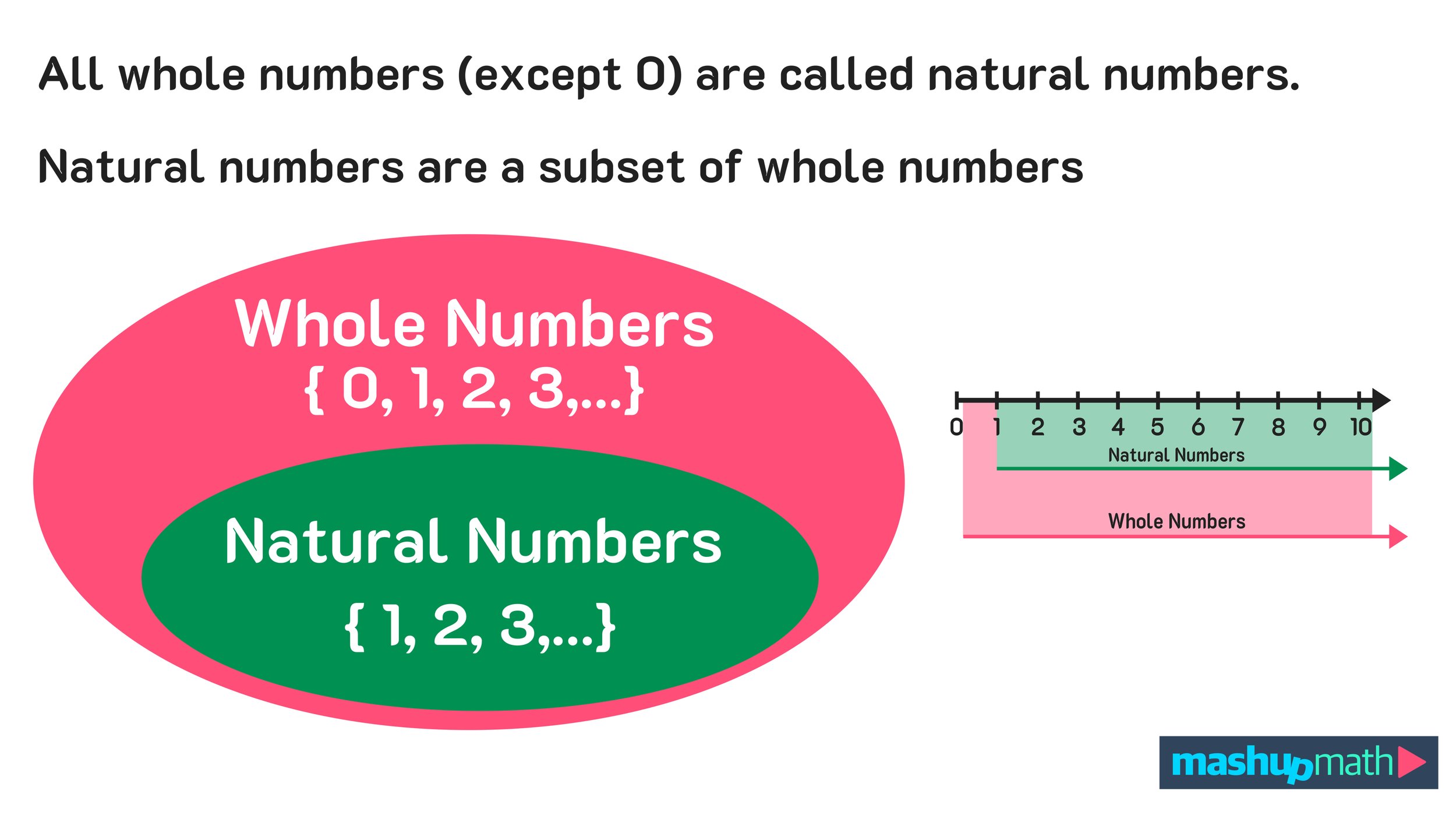
Simply put, the set of whole numbers is just the entire set of natural numbers with zero included.

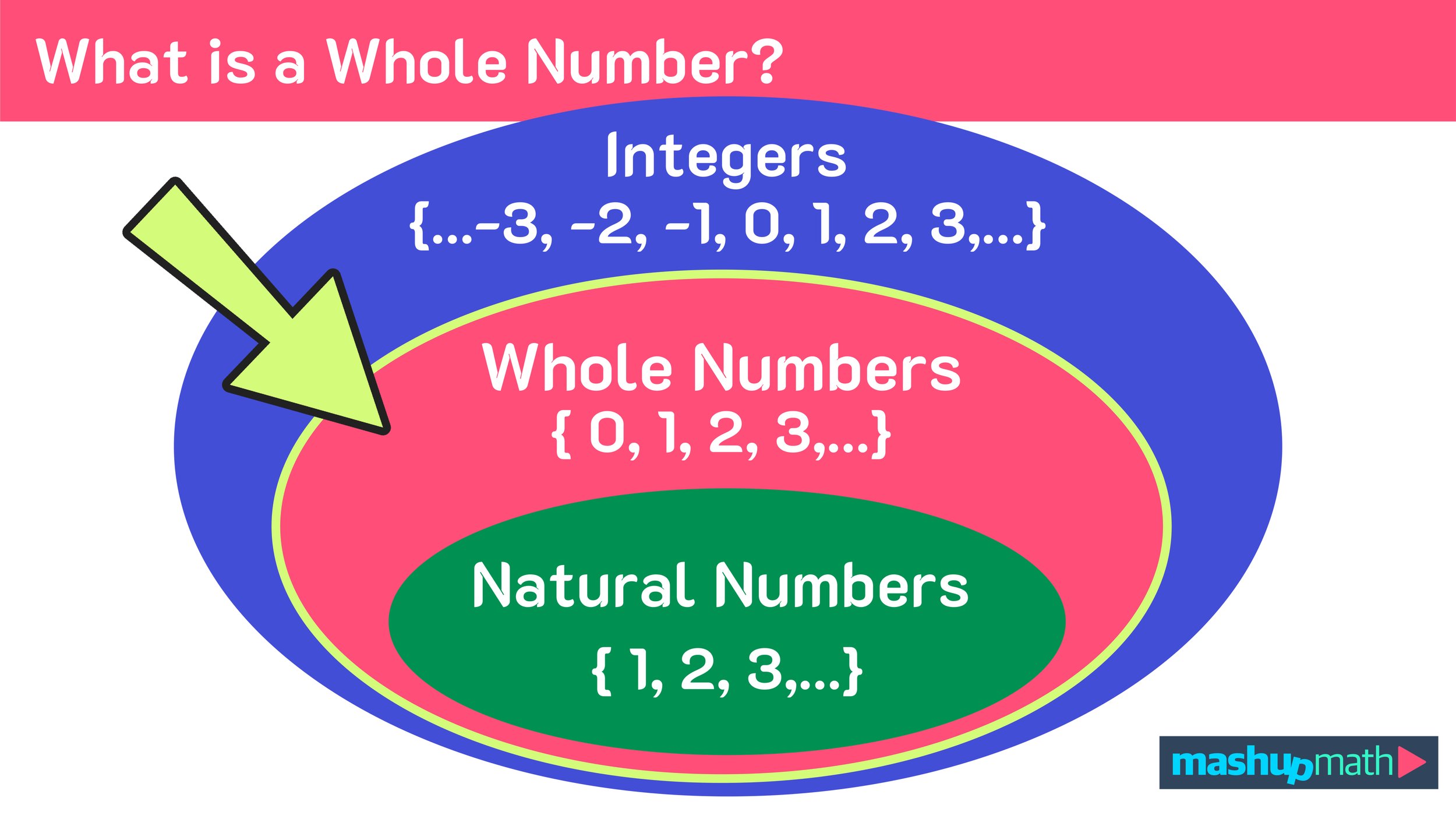
With this in mind, we can say that the set of natural numbers is a subset of the set of whole numbers, which is why the diagram in Figure 03 below is often used to demonstrate this relationship.

 

Figure 03: Natural numbers are a subset of whole numbers. All whole numbers (except zero) are natural numbers too.

 

The Role of Zero: Is 0 a Whole Number?

Next, let's explore commonly asked question regarding whole numbers: Is zero a whole number? The answer to this quest is yes!

Zero is a whole number.

When it comes to the universe of numbers (and its subsets), the value zero is important because it represents a quantity of “nothing” or an empty set. In the case of whole numbers, zero is the dividing point that separates the positive numbers from the negative numbers (since zero is neither positive or negative).

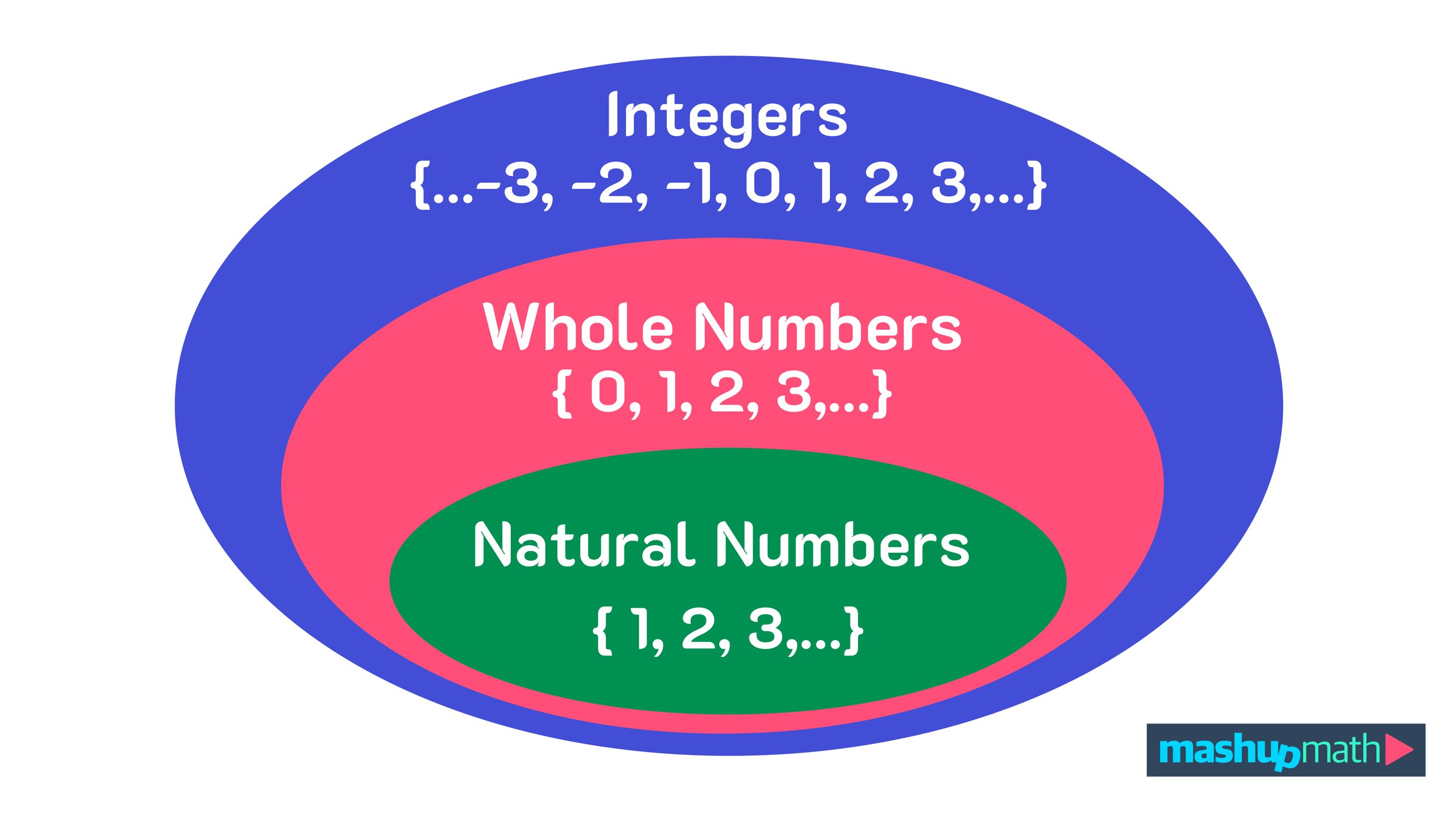
As you continue to study the universe of numbers, you will continue to consider negative numbers and the set of integers, which includes all zero, all of the natural numbers, and their negative counterpart.

The set of integers in comparison to whole numbers and natural numbers, as well as the role of zero, is shown in Figure 04 below.

The set of integers does not include any values with fractional or decimal part. It does not have a starting point and is as follows {…,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,…}

Figure 04: Is zero a whole number? Zero is a whole number and an integer as well.

Figure 05: Whole numbers and natural numbers are subsets of integers.

Examples of Whole Numbers

Now you are ready to extend your understanding of whole numbers to a few examples with real-world context:

  • Example #1: The number of members in the chess club. You can’t have a fraction of a person or a negative person as a member of a club, so the number used to describe the number of members will always be a whole number such as 7 or 12. And, of course, if nobody joins the chess club, you could say that there are zero members.

  • Example #2: The amount of marbles in a bag. You can’t have a fraction of a marble or a negative marble, so the number used to describe the amount of marbles in a bag will always be a whole number such as 22 or 60. And, if the bag is empty, you could say that the amount of marbles is zero.

  • Example #3: The number of cars for sale at a dealership. Again, it is not possible to have a fraction of a car or a negative car, so the number of cars for sale will be a whole number such as 5 or 116. If all of the cars are sold and there is nothing for sale at the dealership at any point in time, then the amount of cars for sale can be zero.

 

Figure 07: Whole Numbers in the Real-World: The number of cars available for sale at a dealership will always be a whole number such as 25 since it’s impossible to have a fraction of a car or a negative car and the amount of cars available can be zero if the lot is empty. Photo by Alex Suprun on Unsplash

 

Conclusion: What is a Whole Number in Math?

In math, the universe of numbers can be broken into several subsets.

The most basic of these subsets are the Natural Numbers (also known as counting numbers), which related to elementary finger counting as follows: {1, 2, 3, 4, 5, …}.

Whole numbers are a set of numbers that includes all of the natural numbers as well as 0.

Unlike the set of natural numbers, which starts at 1, the set of whole numbers starts at 0 and is as follows: { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, …}. Whole numbers can not be fractions or negative.

The set of whole numbers is just the entire set of natural numbers with zero included and we can say that the natural numbers are a subset of whole numbers.

While not a natural number, zero is a whole number and it plays an important role in the universe of numbers as a divider/boundary between the positive numbers and the negative numbers.

This understanding of whole numbers will help you as you continue on with your study of real numbers and their subsets, especially your next likely destination: integers.

 
 

More Free Resources You Will Love:

Why Am I So Bad at Math? (And How to Get Better)

If you are wondering, why am I so bad at math? The fault is likely due to you having a fixed mindset for learning, which is often a product of being negatively affected by harmful misconceptions about your ability to learn math.

What is Finite Mathematics?

What is Finite Mathematics?

What is Finite Mathematics?

This Fascinating Field of Study Focuses on Math Concepts in the Finite Universe and Has Tremendous Real-World Applications.

 

What is Finite Mathematics? (Image: Mashup Math FP)

 

Math can be a challenging subject, especially at the college level, but it can also be incredibly rewarding as the subject has practical applications that are useful in essentially every career path imaginable. This post will explore Finite Mathematics, what it entails, how difficult it is, and how it differs from calculus.

What is Finite Mathematics?

Finite Mathematics is an extremely interesting branch of math that primarily deals with concepts applicable to the finite (as opposed to infinite) universe. Despite its technical name, finite mathematics is primarily concerned with applying mathematics problem-solving and reasoning to real-world phenomena, making it a critical area of knowledge for students pursuing careers in business, social sciences, computer science, and other practical career disciplines.

 

What is Finite Mathematics? Photo by Antoine Dautry on Unsplash

 

Typical Finite Mathematics courses will cover any or all of the following math topics:

  • Linear algebra: This topic focuses on vectors, vector spaces, linear transformations, and systems of linear equations. Linear algebra is integral to various fields of study ranging from business economics to applied physics.

  • Set theory: This topic focuses on the study of sets, or collections of distinct numbers/objects. Set theory serves as a key foundation to several branches of mathematics.

  • Combinatorics: This topic is the study of counting, arrangement, and combination of numbers/objects including permutations, combinations, and counting principles.

  • Probability: This topic focuses on the analysis of uncertainty and random occurrences. The study of probability is a cornerstone of statistics.

  • Graph theory: This topic focuses on the exploration of graphs and is highly applicable in computer science, where data structures are often represented in graphical form.

  • Logic: While more abstract, this topic focuses on formalizing mathematical statements and investigating their validity in a mathematical/systematic way.

  • Matrix algebra: This topic focuses on the study of matrices and their algebraic properties. Matrix algebra is closely tied to linear algebra.

  • Finite calculus or difference equations: This topic focuses on discrete change, such as sequences and series. Finite calculus is often a precursor to calculus, which deals with the infinite universe.

Before moving on, it is worth noting that not all Finite Mathematics courses or textbooks will cover all these topics.

 
 

Is Finite Mathematics Hard?

As with any math course, the difficulty level of Finite Mathematics varies from student to student. Since Finite Mathematics relies heavily on logical reasoning, critical thinking, and the application of math formulas and algorithms, the difficulty is often directly related to how well you understand these related topics. If these areas are your strengths, you will likely find Finite Mathematics appropriately challenging for you (i.e. not too hard and not too easy).

Still, Finite Mathematics can be tricky at times even if you are proficient in logical reasoning, critical thinking, and the application of math formulas and algorithms. Why? Because, as previously mentioned, Finite Mathematics courses often cover a diverse range of topics that require students to be proficient in a variety of math skills and concepts.

However, with the right attitude and approach, most students can be successful in Finite Mathematics and you are likely to struggle much less than you would in a typical Calculus course. In any case, it is always important to remember that, when it comes to mathematics, once you understand the basic principles, more complex ideas become easier for you to grasp.

 

Is finite mathematics hard? Like any math course, the difficulty level will vary from student to student. Photo by Matt Wildbore on Unsplash

 

Finite Mathematics vs. Calculus

So, what is the difference between Finite Mathematics and calculus?

The main difference between Finite Mathematics and calculus is the subject of infinity. Finite Mathematics restricts itself to finite sets, meaning that it does not explore the concept of infinity or infinite sets. On the other hand, calculus delves into the concept of infinity to describe continuous change.

In essence, Calculus takes the study of Finite Mathematics to the next level, which is why it is typically considered to be a more complex and challenging field of mathematics.

Because calculus is more complex than Finite Mathematics, it is often divided two sections: differential calculus and integral calculus. The topics covered in calculus are fundamental to physics, engineering, and economics, among other fields.

In contrast, Finite Mathematics focuses on discrete phenomena related to the finite universe of numbers. Unlike calculus, which focuses on exploring and describing smooth and continuous change, Finite Mathematics excels at analyzing distinct elements and systems that are countable and often rooted in real-world scenarios and data. As such, the topics covered in finite mathematics are often applicable to computer science, statistics, and operations research.

Despite these differences, Finite Mathematics and calculus share a very strong common foundation rooted in the exploration and application of logic and mathematical reasoning.

 

The skills taught in finite mathematics are often applicable to the field of computer science and research. Photo by Mohammad Rahmani on Unsplash

 

Conclusion: Finite Mathematics

In conclusion, whether or not Finite Mathematics is the right math course for you depends on your math skill level, personal interests, career aspirations, and comfort with mathematical logic and reasoning. While not as complex as calculus, Finite Mathematics is an engaging course with many real-world and career-relevant applications. Mastering this field of math will allow you to continue to pursue careers in a variety of desirable fields and industries. With the right mindset and approach, and a willingness to challenge yourself, you are likely to find the journey that is Finite Mathematics to be both valuable and rewarding.

More Free Resources You Will Love:

Why Am I So Bad at Math? (And How to Get Better)

If you are wondering, why am I so bad at math? The fault is likely due to you having a fixed mindset for learning, which is often a product of being negatively affected by harmful misconceptions about your ability to learn math.

Bigfoot Sightings Map —Decoding Bigfoot's Trail Using Data

Bigfoot Sightings Map —Decoding Bigfoot's Trail Using Data

Decoding Bigfoot's Trail: How a Bigfoot Sightings Map Can Predict Bigfoots Whereabouts

Where is Bigfoot? By analyzing a comprehensive Bigfoot Sighting Map, you can see where sightings and concentrated and better predict Bigfoot’s movements and up-to-date location.

 

Bigfoot Sighting Map Courtesy of the Bigfoot Mapping Project (click to enlarge). Screenshot from www.bigfootmap.com.

 

Today’s post will focus on tracking the elusive Bigfoot, a creature that has managed to keep humanity on our toes for hundreds of years. And our tool for tracking the movements and potential locations of Bigfoot will be a detailed and comprehensive map of bigfoot sightings that will allow you to visualize and potentially predict Bigfoot's next move.

The legendary creature known as Bigfoot has been sighted in many parts of North America, leading to numerous theories about his movement patterns and general whereabouts. Bigfoot’s location has been an ongoing mystery that continues to baffle scientists and enthusiasts alike as it remains unclear whether or not Bigfoot is continuously on the move or if there are multiple Bigfoot-like creatures scattered around North America.

Given the mystery surrounding Bigfoot and his whereabouts, looking at a comprehensive bigfoot sighting map is great way to make educated and scientific predictions and conclusions about Bigfoot, his movements, and his location at any given time.

Bigfoot Sightings Map: Is Bigfoot a migratory creature? Does he stay in one place or is he nomadic? Is there more than one Bigfoot? Photo by Ayako on Unsplash

A Bigfoot sightings map is a two-dimensional grid that depicts all of the landmass of North America and has points plotted at all of the geographical locations where a Bigfoot sighting has been reported. Every plotted point represents one reported Bigfoot sighting. And, by compiling all of these sightings on a map, you can use the data to see where sightings are concentrated and also track/predict Bigfoot’s movement patterns.

Why is the Bigfoot sightngs map such a useful tool? From a scientific and mathematical standpoint, patterns often hint at reliability and predictability, and this is where any serious analysis of determining Bigfoot’s whereabouts should begin.

Analyzing a map of Bigfoot sightings can give you important and incredibly useful insights into Bigfoot's preferred geological living environment, potential movement patterns, and, most importantly, his current location.

Bigfoot Sighting Map: Concentrated sightngs in the Pacific Northwest

Additionally, the sightings map can help you to determine if there are certain geological features favored by Bigfoot. For example, does he prefer dense forests over open plains? Does he prefer to be near major water sources, cave systems, weather conditions, etc.? Does Bigfoot tend to appear during specific seasons or times of day?

By better understanding these questions and there potential answers, you have a much better chance of determining Bigfoot’s current location at any given point in time.

Many Bigfoot sightings have been reported in the dense, remote forests of the Pacific Northwest regions of the United States and Canada. This pattern could suggest that Bigfoot prefers forested areas far from human habitation, perhaps for shelter or food resources. The more we understand these patterns, the better we can predict where he might show up next.

 

Image: Mashup Math MJ

 

Of course, analyzing a Bigfoot sighting map isn't just about connecting dots or plotting points on a grid. The map itself is only a tool and it requires an understanding of the geographical, climatic, and ecological factors at play. Are there abundant food sources in the areas of reported sightings? What's the population density like? Answers to such questions deepen our understanding of Bigfoot's behavior and raise new questions as well.

In the case of being a Bigfoot detective and using science and data to track the elusive being, we are not merely passive observers, but active participants attempting to unravel the mysteries of Bigfoot's existence. And, in doing so, we contribute to the larger discourse on Bigfoot and his alleged movements.

Bigfoot Sighting Map: Is Bigfoot a migratory creature? Are there multiple Bigfoots?

As organizations continue to collect and analyze sightings data, a Bigfoot sighting map becomes an ever-evolving tool, gaining in accuracy and detail. It's a testament to the collective efforts and scientific curiosity of the Bigfoot community.

However, it is also important to note that, while it's easy to get caught up in the thrill of the chase, it's important to approach each reported sighting with a healthy dose of skepticism. Always consider the source and the circumstances of the sighting. Not every footprint in the mud belongs to Bigfoot.

If you are looking for an interactive and comprehensive Bigfoot map that is constantly updated, we recommend the Bigfoot Mapping Project’s website, where you can see up-to-date Bigfoot sightings, analyze geographical features such as elevation, and report a sighting of your own!

Source: The Bigfoot Mapping Project via https://www.bigfootmap.com

More Free Resources You Will Love:

Search Tags: bigfoot, bigfoot sightings map, bigfoot sitghing map, bigfoot sighting map, map of bigfoot sightings, bigfoot map, bigfoot on google maps

10 Awesome Math Project Ideas for Grades 1-8

18 Comments

10 Awesome Math Project Ideas for Grades 1-8

Fun Math Projects for All Grade Levels

Are you looking for fun math project ideas for your students?

Math Projects for Middle School, Elementary School, and High School Students.

The following list of math project ideas are perfect for keeping your students engaged during the final weeks of the school year (or at any other time as well). These activities can be adapted to all grade and ability levels and are included in our 21 Time-Saving Strategies, Activities, and Ideas All Math Teachers Should Know.

Having students work on fun math projects (and math art projects) is a great way to keep their attention and break up the monotony of the normal classroom routine.

The following math project ideas for elementary school, middle school, and high school students can all be modified to appropriately challenge and engage your math students based on their interests and skill/ability levels. We highly recommend that you differentiate whatever math project you choose to best meet the needs of your students.

Now, are you ready to learn about some fun math projects that you can use to engage your students this school year?

(Do you want free K-8 math resources and activities in your inbox every week? Click here to sign up for our free math education email newsletter)

1.) The Ultimate Paper Airplane Competition

Grade Levels: Grades 1-8+

Description: Working individually or collaboratively, students must construct a paper airplane that is best suited for distance, accuracy, and hang time. This project involves a research phase, experimentation, data collection, analysis, and a presentation. This project is great for the end of the school year when the weather is nice and students can test their paper airplane performance outdoors.

Click here to learn more about the Ultimate Paper Airplane Competition Project

Math Project Ideas: The Ultimate Paper Airplane Competition. (Image: Mashup Math FP)

2.) Dream Home Design Project

Grade Levels: Grades 1-8+

Description: For this fun math art project, students are tasked with designing the floor plans for their dream homes and backyards by applying math skills including measurement, scale, area, and perimeter. Students can use graph paper and markers or digital tools like Google Sketchup to create their home’s blueprints, calculate the cost of building materials and furniture, and design the layout of their houses interior and exterior.

You can modify the project based on your students’ grade, skill, or ability level as well as your access to resources. You can also have students design a city, amusement park, dining hall, etc.

Math Project Ideas: Dream Home Design. (Image: Mashup Math FP)

3.) Math Riddles, Puzzles, and Brain Teasers!

Grade Levels: Grades K-8

Description: Spend a day having your students work on super fun and challenging math riddles and brain teasers. I like to print out the activities and post them around my classroom and/or in the hallways and have my students travel from station to station attempting to solve each brain bender!

Here are a few links for access free grade and topic-specific math riddle and brain teaser worksheets:

 

Math Projects for Middle School Students: Puzzles, Riddles, and Brain Teasers

 

4.) Play Math Jeopardy!

Grade Levels: Grades 3-6

Description: Are your students ready to play Math Jeopardy? These fun interactive Jeopardy games include a hidden Daily Double question as well as a Final Jeopardy video question.

Click the links below to play Math Jeopardy for the following grade levels:

Math Project Ideas: Math Jeopardy!

Do you more FREE K-8 math resources and activity ideas in your inbox every week?

 
 

5.) Budgeting Your Dream Vacation

Grade Levels: 4-8+

Description: For this project, give your students a budget that they have to spend on their dream vacation for just themself and a friend. Students will have to research the cost of travel, lodging, meals, and leisure activities to cover a 7-10 day vacation to a location of their choosing.

Math Project Ideas: Budget and Plan Your Dream Vacation. (Image: Mashup Math MJ)

6.) Build a Fraction Kit

Grade Levels: 3-8+

Description: Building a fraction kit using colored construction paper is one of the best ways to help your students to understand math concepts related to fractions, including simplifying fractions, equivalent fractions, comparing fractions, and adding and subtracting fractions.

Click here to for step-by-step instructions on building a fraction kit

 
Image via www.mashupmath.com

Image via www.mashupmath.com

 

7.) Math Card Games!

Grade Levels: 3-8+

Description: Spend a day having your students engage in fun math games that require only a standard deck of playing cards to play. Here are a few fun ideas:

Math Project Ideas: Play Math Card Games. (Image: Mashup Math FP)

8.) Create Your Own Math Board Game

Grade Levels: 2-8+

Description: For this math project, students are tasked with creating their own math-related board games based on an assigned topic/skill or one of their choosing. To complete this project, students must choose a concept, plan their game, create a game board, design the game pieces, uses spinners or dice to determine how players will navigate the board, test and revise the game, and present their final product to the class.

Math Project Ideas: Create Your Own Math Board Game! (Image: Mashup Math FP)

9.) History of Math Research Project

Grade Levels: 1-8+

Description: For this project, students will research and present on a famous individual or civilization and their contributions to the field of mathematics. Here are a few great resources for inspiring students to learn about some lesser know mathematicians and their amazing contributions to mathematics:

 

Math Project Ideas: Make a presentation about a famous mathematician like Sir Isaac Newton. (Image: Mashup Math MJ)

 

10.) Stock Market Project

Grade Levels: 4-8+

Description: For this financial math project, students must build their own 10-stock portfolio using a $10,000 budget. Students must research and analyze publicly traded companies and their stock performances to make their picks. They can invest in companies that they are familiar with such as Netflix, Facebook, McDonalds, and more!

We recommend showing this short TED-Ed Video How Does the Stock Market Work and using Google to research companies, find stock symbols, and see corresponding graphs and charts.

 

Math Project Ideas: Stock Market Project (Image Source: Google Stocks)

 

More Math Education Insights You Will Love:

Search Tags: math art projects, math projects for middle school, math projects, math project ideas, 21st century math projects, middle school math projects, math projects for 5th graders

18 Comments

The Paper Airplane Game: Fun Project for Students

The Paper Airplane Game: Fun Project for Students

The Ultimate Paper Airplane Project

Research, Experiment, Optimize, and Test Your Design to Win the Paper Airplane Game

 

What is the paper airplane game? The paper airplane game is a project involving math and physics where students attempt to create a paper airplane that excels in distance, accuracy, and hang time. (Image: Mashup Math FP)

 

The Paper Airplane Game: The Ultimate Paper Airplane Math Project is a hands-on and fun exploration of the mathematics and physics behind designing and creating a paper airplane that can travel long distances, fly accurately, and stay in the air as long as possible.

The paper airplane game is great for all ages and is a popular math project activity for elementary and middle school students. The only resources required are paper, scissors, a stopwatch, measuring tape, and having access to an open space (indoor or outdoor) where students can fly their paper airplanes.

Here is how the project works:

Paper Airplane Game Stage 1: Research

The very first stage of the paper airplane game involves researching the physics and mathematics behind what allows airplanes to take flight. During this stage, students are exposed to key concepts including lift, drag, thrust, and the impact of weight.

This stage is meant to spark student interest and inspire their designs. We recommend showing the following 5-minute TED-Ed video How Do Airplanes Actually Fly?

 
 

Paper Airplane Game Stage 2: Experiment

The second stage of the paper airplane game is experimenting. During this phase, students are given the freedom to play with different styles and designs to make paper airplanes. Students have the option to follow classic designs or to create their own unique designs and then use trial-and-error to test how different shapes and folds affect how a paper airplane travels.

 
 

Paper Airplane Game Stage 3: Collect Data

During the third stage, students are tasked with collecting data about their paper airplane designs. Using a stopwatch and measuring tape, students can track data about how far their plane traveled, how long it stayed in the air, and how accuratly it flies when being thrown at a target.

Paper Airplane Game Stage 4: Data Analysis

Once enough data has been collected, students are ready to analyze their results to make conclusions about the viability of their designs. Students should be encouraged to use math formulas and to make calculations to draw meaningful conclusions and to determine which design is best for the final competition.

Paper Airplane Game Stage 5: Optimize Your Design

Based on students analysis of their collected data, they should be given one final opportunity to optimize their paper airplane designs to maximize their plans distance, accuracy, and air time. Students may want to combine the best features from multiple designs into one final product. Students can also practice throwing their final design and see how different throwing techniques affect the flight patterns.

 

Image: Mashup Math FP

 

Paper Airplane Game Stage 6: Compete

Finally, students can have their final paper airplane designs compete against each other in three categories:

  • farthest distance traveled

  • accuracy (how close a thrown plane can get to hitting a given target)

  • air time (which plane can stay in the air the longest before hitting the ground)

Students can also present their final designs to the class and explain what they learned by going through the research, experimenting, data collection and analysis, and optimization phases.

More Free Resources You Will Love:

Why Am I So Bad at Math? (And How to Get Better)

If you are wondering, why am I so bad at math? The fault is likely due to you having a fixed mindset for learning, which is often a product of being negatively affected by harmful misconceptions about your ability to learn math.