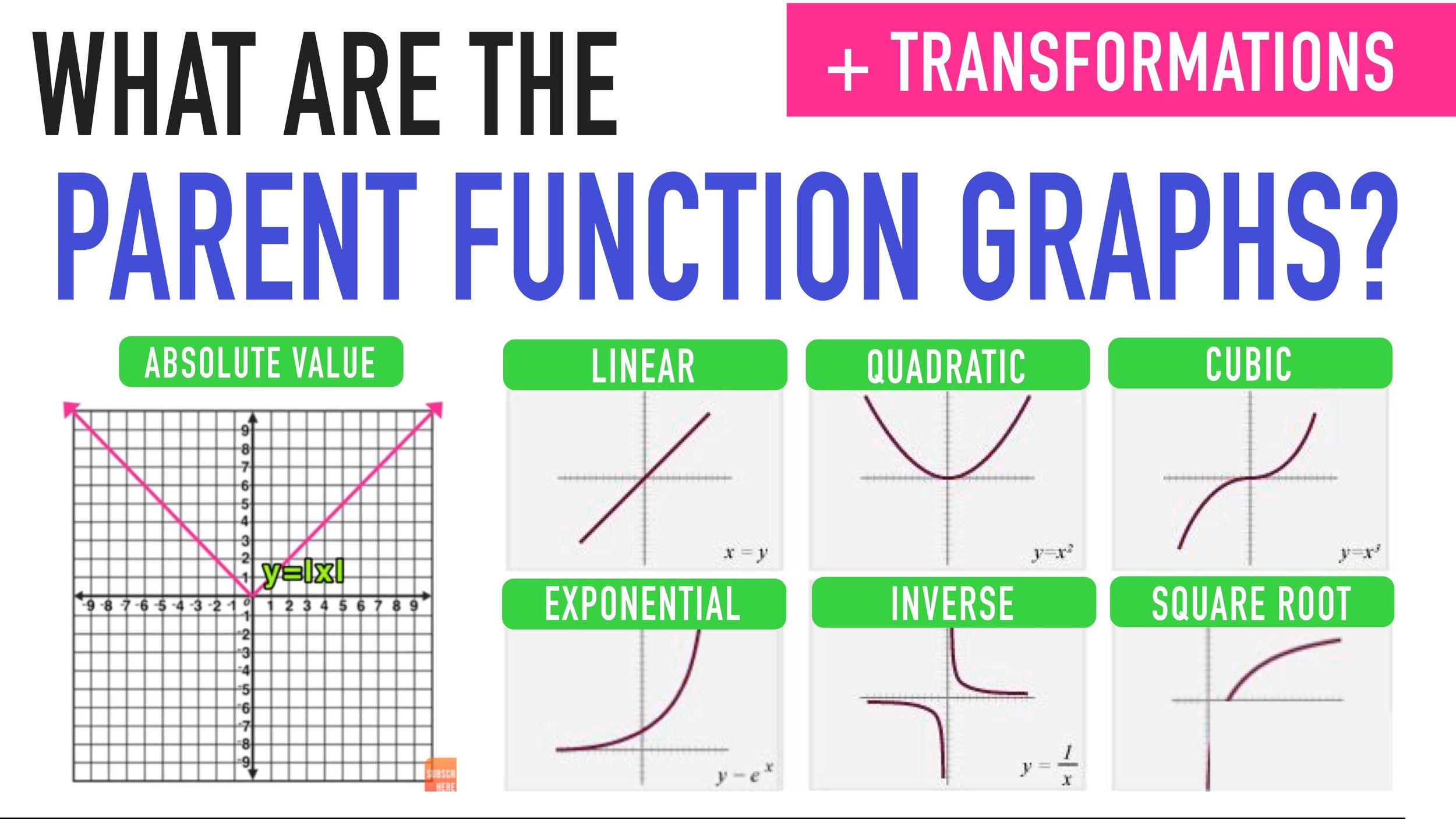
How to Complete the Square in 3 Easy Steps

How to Complete the Square in 3 Easy Steps

Step-by-Step Guide: How to do Completing the Square

Step-by-Step Guide: How to Complete the Square Explained.

As you continue onto more advanced problems where you have to factor quadratics, you will have to learn how to complete the square in order to find correct solutions. Completing the square is a special technique that you can use to factor quadratic functions.

This free step-by-step guide on How to Complete the Square will teach you an easy 3-step method for factoring any quadratic using a technique called “completing the square.”

This guide will focus on the following topics and sections. You can click on any of the text links below to jump to one particular section, or you can follow each section in sequential order.

• What is Completing the Square?

• How to Complete the Square Example #1: x² - 6x -16 = 0

• How to Complete the Square Example #2: x² +12x +32 = 0

• How to Complete the Square Example #3: x² +2x -7 = 0

Let’s begin by exploring the meaning of completing the square and when you can use it to help you to factor a quadratic function.

Figure 01: Are you ready to learn how to find solutions to quadratic equations by completing the square?

What is Completing the Square?

Completing the square is a method that you can use to solve quadratic equations of the form ax² + bx + c = 0 (where a, b, and c are all not equal to zero).

❗Note that the equations of the form ax² + bx + c = 0 are called quadratic equations and they can be rewritten as follows:

• ax² + bx + c = 0

• ax² + bx = -c

Both of these equations are equivalent to each other, and understanding the relationship between these two equations will help you to understand how to complete the square later on in this guide.

In the next section, we will work through three examples of how to complete the square using the following 3-step method:

• Step #1: Rearrange the quadratic equation so that all of the constants are on one side of the equals sign.

• Step #2: Add (b/2)² to both sides of the equal sign.

• Step #3: Factor and solve.

By solving a quadratic equation by completing the square, you are identifying values where the parabola that represents the equation crosses the x-axis.

As long as you understand how to follow and apply these three steps, you will be able to solve quadratics by completing the square (provided that they are solvable). Now, let’s gain some experience with using the three step method on how to complete the square by working through some step-by-step practice problems.

Figure 02: The solutions to a quadratic equation are the values where the graph crosses the x-axis.

---

How to Complete the Square: Example #1

Solve: x² - 6x -16 = 0

For this first example (and all of the practice problems in this guide), we can solve the problem by completing the square using our three step method as follows:

Step #1: Rearrange the quadratic equation so that all of the constants are on one side of the equals sign.

Let’s start off by noticing that our given quadratic function is indeed in ax² +bx + c = 0 form, where a=1, b=-6, and c=-16.

To complete the first step, we have to move all of the constants (all of the values not attached to variables, to the right side of the equals sign as follows:

• x² - 6x -16 = 0

• x² - 6x -16 (+16) = 0 (+16)

• x² - 6x = 16

Now we have completed the first step and we are left with a new equivalent equation:

• x² - 6x = 16

Step #2: Add (b/2)² to both sides of the equal sign.

For the next step, we have to find the value of (b/2)² and add it to both sides of the equals sign.

Since we know that b=-6, we can find the value of (b/2)² by substituting -6 for b as follows:

• (b/2)²

• (-6/2)²

• (-3)²

• =9

In this case, (b/2)² = 9, so, to complete Step #2, we simply have to add 9 to both sides of the equal sign as follows:

• x² - 6x = 16

• x² - 6x + 9 = 16 + 9

• x² - 6x + 9 = 25

Figure 03: How to Complete the Square in 3 Easy Steps.

Step #3: Factor and solve.

Finally, we are ready for the third and final step where we just need to factor and solve.

Notice that the left side of the equation of x² - 6x + 9 = 25 is a trinomial that is factorable as follows:

• x² - 6x + 9 = (x-3)(x-3)

• x² - 6x + 9 = (x-3)²

In this example, the factors of x² - 6x + 9 are (x-3)(x-3), which we will express as (x-3)² since it will allow us to solve the problem as follows:

• x² - 6x + 9 = 25

• (x-3)² = 25

• √[(x-3)²] = √[25]

• x -3 = ± 5

In the third step above, we took the square root of both sides of the equation to remove the exponent and we are left with x -3 = ± 5, which means that

• x - 3 = 5

• x - 3 = -5

We can now find the solutions to this first example by solving both equations as follows:

• x - 3 = 5 → x = 8

• x - 3 = -5 → x = -2

All three steps for how to do completing the square are shown in Figure 03 above.

Now, we can conclude that the original quadratic equation x² - 6x -16 = 0 has two solutions:

Final Answer: x = 8 and x = -2

This means that the graph of the equation x² - 6x -16 = 0 will be a parabola that crosses the x-axis at both (-2,0) and (8,0) as shown in Figure 04 below.

Figure 04: How to solve by completing the square: graph explanation

---

How to Complete the Square: Example #2

Solve: x² +12x +32 = 0

We can solve this next example using our 3-step method, just as we did in the previous example, as follows:

Step #1: Rearrange the quadratic equation so that all of the constants are on one side of the equals sign.

Notice for our given quadratic equation, x² +12x +32 = 0, that a=1, b=12, and c=32.

Since our constant c is on the left side of the equation, we simply have to move it to the right side using inverse operations to complete Step #1.

• x² +12x + 32 = 0

• x² +12x + 32 (-32) = 0 (-32)

• x² + 12x = -32

After completing the first step, we now have:

• x² + 12x = -32

Step #2: Add (b/2)² to both sides of the equal sign.

Next, we have to add (b/2)² to both sides of our new equation.

In this example, b=12, so we can find the value of (b/2)² as follows:

• (b/2)²

• (12/2)²

• (6)²

• =36

Since (b/2)² = 36, we can complete Step #2 by adding 36 to both sides of the equation as follows:

• x² + 12x = -32

• x² + 12x +36 = -32 +36

• x² + 12x +36 = 4

Figure 05: How to complete the square to find the solutions to a quadratic equation.

Step #3: Factor and solve.

For the final step, we just have to factor and solve for any potential values of x.

Just like example #1, we can finish completing the square by factoring the trinomial on the left side of the equation and then solving.

In this case, the trinomial on the left side of the equation can be factored as follows:

• x² + 12x +36 = (x+6)(x+6)

• x² + 12x +36 = (x+6)²

❗Note that whenever you solve a problem using the complete the square method, you will always end up with two identical factors when you complete Step #3.

Now that we know that the factors of x² + 12x +36 are equal to (x+6)², we can solve for x as follows:

• x² + 12x +36 = 4

• (x+6)² = 4

• √[(x+6)²] = √[4]

• x + 6 = ± 2

In this case, the original quadratic function x² +12x +32 = 0 will have two solutions:

• x + 6 = 2

• x + 6 = -2

We can determine these two solutions by solving each equation as follows:

• x + 6 = 2 → x = -4

• x + 6 = -2 → x = -8

The entire 3-step method for completing the square for Example #2 is shown in Figure 05 above.

Final Answer: x = -4 and x = -8

Figure 06 below shows the graph of the parabola represented by x² +12x +32, with x-intercepts at -4 and -8.

Figure 06: Solving a quadratic by completing the square helps you to find the x-intercepts of the parabola that represents the equation.

---

How to Complete the Square: Example #3

Solve: x² +2x -7 = 0

Are you starting to get the hang of how to complete the square? Let’s gain some more experience with this next example.

Step #1: Rearrange the quadratic equation so that all of the constants are on one side of the equals sign.

For this problem, we know that a=1, b=2, and c=-7.

For our first step, let’s rearrange the equation so that all of the constants are on the right side:

• x² +2x -7 = 0

• x² +2x -7 (+7) = 0 (+7)

• x² + 2x = 7

Now we have a new equivalent function:

• x² + 2x = 7

Step #2: Add (b/2)² to both sides of the equal sign.

Now we need to add (b/2)² to both sides of the equation. Since b=2 in this example, (b/2)² is equal to:

• (b/2)²

• (2/2)²

• (1)²

• =1

Since (b/2)² = 1, we can complete the second step by adding 1 to each side of the equation as follows:

• x² + 2x = 7

• x² + 2x +1 = 7 +1

• x² + 2x +1 = 8

Figure 07: How to Complete the Square: Solutions will not always be rational numbers.

Step #3: Factor and solve.

Now we are ready to factor and solve the equation.

We have a trinomial on the left side of the equation that can be factored as follows:

• x² + 2x +1 = (x+1)(x+1)

• x² + 2x +1 = (x+1)²

With these factors in mind, we can solve for x as follows:

• x² + 2x +1 = 8

• (x+1)² = 8

• √[(x+1)²] = √[8]

• x +1 = ± √[8]

For this third example, the quadratic function x² +2x -7 = 0 will have two solutions:

• x + 1 = √[8]

• x + 1 = - √[8]

If we continue onto solving these two equations, we will see that, unlike Examples #1 and #2, we do not end up with a rational answer:

• x + 1 = √[8] → x = -1 + √8

• x + 1 = - √[8] → x = -1 - √8

In cases like this, you can often conclude that:

Final Answer: x = -1 + √8 and x = -1 - √8

The solutions above are considered exact answers. However, if you are trying to estimate where the parabola will cross the x-axis on the coordinate plane, you could take the problem a step further by approximating for √8 as follows:

• √8 ≈ 2.83

• x = -1 + √8 → x = -1 + 2.83 → x =1.83

• x = -1 + √8 → x = -1 - 2.83 → x =-3.83

Now we have two approximate solutions for x:

• x =1.83 and x=-3.83

What does this mean? Just like we saw in Examples #1 and #2, the solutions tell you where the graph of the parabola crosses the x-axis. In this example, the graph crosses the x-axis at approximately 1.83 and -3.83, as shown in Figure 08 below.

Figure 08:  How to complete the square to determine the solutions to a quadratic equation.

---

Conclusion: How to Complete the Square

When learning how to solve quadratic equations of the form ax² + bx +c=0, understanding how to complete the square to find the values where x=0 is an important and useful algebra skill that you can use to solve a variety of problems.

Whenever you have an equation in ax² + bx +c=0 form, you can solve it by following these 3-simple steps to completing the square:

• Step #1: Rearrange the quadratic equation so that all of the constants are on one side of the equals sign.

• Step #2: Add (b/2)² to both sides of the equal sign.

• Step #3: Factor and solve.

Note that the above 3-step method for completing the square can be used to find the solutions of any quadratic equation of the form ax² + bx +c=0. These solutions represent the x-values where the parabola that represents the equation crosses the x-axis.

Keep Learning:

How to Find the Vertex of a Parabola in 3 Easy Steps

Learn how to find the coordinates of the vertex point of any parabola with this free step-by-step guide.

---

How to Find Horizontal Asymptotes in 3 Easy Steps

How to Find Horizontal Asymptotes in 3 Easy Steps

Step-by-Step Guide: How to Find the Horizontal Asymptote of a Function

Step-by-Step Guide: How to Find the Horizontal Asymptotes of Functions.

During your study of algebra, you will eventually learn how to analyze and understand the behavior functions when they are represented graphically on the coordinate plane. The graph of a function gives you a visual portrayal of how the function behaves—including the location of any potential horizontal asymptotes.

This free step-by-step guide on How to Find Horizontal Asymptotes of a Function will demonstrate and explain everything you need to know about horizontal asymptotes and how to find the horizontal asymptote of any function (assuming that the function does indeed have a horizontal asymptote).

The following sections will be covered in this guide. While we recommend that you work through each section in order, you can use the quick-links below to jump to a particular section":

• What is a Horizontal Asymptote?

• How to Find Horizontal Asymptotes Example #1

• How to Find Horizontal Asymptotes Example #2

• How to Find Horizontal Asymptotes Example #3

Let’s start off by learning more about horizontal asymptotes and what they look like.

Figure 01: The horizontal asymptote of a function tells you the behavior of a function as it approaches the edges of a graph.

What is a Horizontal Asymptote?

Before you learn how to find horizontal asymptotes, it is important for you to understand some key foundational concepts.

In algebra, a function is an equation of the form y=f(x) that represents the relationship between two sets. A relation can be defined as a function when there is only one output value for each input value (i.e. the x-values do not repeat). Functions can be visually represented on a graph (i.e. a coordinate plane).

A horizontal asymptote of a function is a horizontal line (↔) that tells you the behavior of a function as it approaches the edges of a graph. We can also say that horizontal asymptotes allow us to identify the “end behavior” of a function.

It is also important to note that horizontal asymptotes occur when functions are rational expressions, meaning that the function is a quotient of two polynomials (i.e. the function is a fraction where both the numerator and the denominator are polynomials.

For example, consider the following function:

• y = (3x²)/x³

Figure 02: The graph of the function y = (3x²)/x³

Our function, y = (3x²)/x³, is the quotient of two polynomials (i.e. it is a rational expression) and its corresponding graph is shown in Figure 02 above.

Since our function is a fraction, we know that we can not have zero in the denominator (otherwise the function would be undefined at this point). So, the graph of the function, as you can see in Figure 02, does something interesting at zero.

In this example, we have a horizontal asymptote at y=0.

Notice how the graph of the function y = (3x²)/x³ gets closer and closer to the line y=0, without ever touching it, as it approaches the ends of the graph (horizontally), as shown in Figure 03 below.

Figure 03: The function has a horizontal asymptote at y=0.

If we take a look at a few points on the graph of y = (3x²)/x³ and the corresponding table, as shown in Figure 04 below, we can see that as the graph moves to the left of the coordinate plane, the y-values get closer and closer to zero. And, we can also see that as the graph moves to the right of the coordinate plane, the y-values get closer and closer to zero.

This type of observation is what we call determining the “end behavior” and it helps us to understand why the graph has a horizontal asymptote at y=0.

Figure 04: How to Find a Horizontal Asymptote of a Function

Now that you understand what a horizontal asymptote is and what it looks like, you are ready to work through a few step-by-step examples of how to find a horizontal asymptote.

Before moving forward, here are a few quick key points you should be familiar with:

• Not all functions that are rational expressions have a horizontal asymptote.

• It is possible for a function to have 0, 1, or 2 asymptotes (i.e. a function can have a maximum of 2 asymptotes).

• When horizontal asymptotes are shown on a graph, they are typically drawn using a dashed line, which is what you will see in this guide.

• The horizontal asymptote of a function is not a part of the function, and it is not a requirement to include the horizontal asymptote of a function when you graph it on the coordinate plane.

• A horizontal asymptote can be thought of as an imaginary dashed line on the coordinate plane that helps you to visual a “gap” in a graph.

Figure 05: A horizontal asymptote is an imaginary line that is not a part of the graph of a function.

---

How to Find Horizontal Asymptotes Example #1

Now you are ready to learn how to find a horizontal asymptote using the following three steps:

• Step One: Determine lim x→∞ f(x). In other words, find the limit for the function as x approaches positive ∞.

• Step Two: Determine lim x→-∞ f(x). In other words, find the limit for the function as x approaches negative ∞.

• Step Three: If one of or both of the limits determined above is a real number, k, then the equation of the horizontal asymptote is y=k for each unique value of k (a function can have 0, 1, or 2 horizontal asymptotes).

Now, let’s go ahead and apply these three steps to our first practice problem.

Example #1: Find the horizontal asymptote of the function f(x)=4x/(x+4)

For this first example, we can start by taking a look at the graph in Figure 05 above. By looking at the graph, we can see that the function f(x)=4x/(x+4) has one horizontal asymptote at y=4.

Let’s now apply our three steps to see if confirm the at the function has a horizontal asymptote at y=4.

Step One: Determine lim x→∞ f(x). In other words, find the limit for the function as x approaches positive ∞.

• lim x→∞ f(x) = lim x→∞ 4x/(x+4)

• = 4 lim x→∞ [1/(1+(4/x))]

• = 4 (lim x→∞ (1)) / (lim x→∞ (1+(4/x))

• = 4 ( (1)/(1))

• =4

After completing the first step, we can see that, as the function has a horizontal asymptote at y=4 as the function approaches positive ∞ on the graph.

Next, let’s confirm that the function has the same behavior as it approaches negative ∞.

Step Two: Determine lim x→-∞ f(x). In other words, find the limit for the function as x approaches negative ∞.

• lim x→-∞ f(x) = lim x→∞ 4x/(x+4)

• = 4 lim x→-∞ [1/(1+(4/x))]

• = 4 (lim x→-∞ (1)) / (lim x→∞ (1+(4/x))

• = 4 ( (1)/(1))

• =4

Completing the second step gives us the same result as the first step (i.e. there is a horizontal asymptote at y=4).

Step Three: If one of or both of the limits determined above is a real number, k, then the equation of the horizontal asymptote is y=k for each unique value of k (a function can have 0, 1, or 2 horizontal asymptotes).

Finally, based on our results from steps one and two, we can conclude that the function has one horizontal asymptote at y=4, as shown on the graph in Figure 06 below.

Final Answer: The function has one horizontal asymptote at y=4.

Figure 06: How to find a horizontal asymptote using limits.

---

How to Find Horizontal Asymptotes Example #2

Find the horizontal asymptote of the function f(x)=3ˣ+5

For this next example, we want to see if the exponential function f(x)=3ˣ+5 has any horizontal asymptotes.

We can solve this problem the same as we did the first example by using our three steps as follows:

Step One: Determine lim x→∞ f(x). In other words, find the limit for the function as x approaches positive ∞.

• lim x→∞ f(x) = lim x→∞ 3ˣ+5

• =lim x→∞ (3ˣ) + lim x→∞ (5)

• lim x→∞ (3ˣ) = ∞

• lim x→∞ (5) = 5

• = ∞ + 5 = ∞

Notice that our result for the first step is that, as the function approaches positive ∞, the limit is ∞. And, since ∞ is not a real number, we can not yet determine whether or not this function will have any horizontal asymptotes. But we can not be completely sure until we complete the second step.

Step Two: Determine lim x→-∞ f(x. In other words, find the limit for the function as x approaches negative ∞.

• lim x→-∞ f(x) = lim x→-∞ 3ˣ+5

• =lim x→-∞ (3ˣ) + lim x→-∞ (5)

• lim x→-∞ (3ˣ) = 0

• lim x→-∞ (5) = 5

• = 0 + 5 = 5

Our result from step number two results in a real number, so we can conclude that the function does have a horizontal asymptote at y=5.

Step Three: If one of or both of the limits determined above is a real number, k, then the equation of the horizontal asymptote is y=k for each unique value of k (a function can have 0, 1, or 2 horizontal asymptotes).

Again, even though Step One did not result in a real number limit, Step Two did, so we can conclude that:

Final Answer: The function has one horizontal asymptote at y=5.

We can confirm the location of a horizontal asymptote at y=5 for the exponential function f(x)=3ˣ+5 by looking at the completed graph in Figure 07 below.

Figure 07: How to find horizontal asymptotes given a function explained.

---

How to Find Horizontal Asymptotes Example #3

Find the horizontal asymptote of the function f(x)=(3x^2+x)/(x+2)

For this third and final example, we have to see if the rational function f(x)=(3x^2+x)/(x+2) has one, two, or zero horizontal asymptotes.

We can determine whether or not the function has any horizontal asymptotes by following our three steps as follows:

Step One: Determine lim x→∞ f(x). In other words, find the limit for the function as x approaches positive ∞.

• lim x→∞ f(x) = lim x→∞ (3x^2+x)/(x+2)

• =lim x→∞ (3x+1)/(1+(2/x))

• = (lim x→∞ (3x+1)) / (lim x→∞(1+(2/x)))

• lim x→∞ (3x+1) = ∞

• lim x→∞(1+(2/x)) = 1

• = ∞ / 1 = ∞

Since our result is not a real number, Step One does not help us to determine the possible existence of a horizontal asymptote.

Step Two: Determine lim x→-∞ f(x. In other words, find the limit for the function as x approaches negative ∞.

• lim x→-∞ f(x) = lim x→-∞ (3x^2+x)/(x+2)

• =lim x→-∞ (3x+1)/(1+(2/x))

• = (lim x→-∞ (3x+1)) / (lim x→-∞(1+(2/x)))

• lim x→-∞ (3x+1) = -∞

• lim x→-∞(1+(2/x)) = 1

• = -∞ / 1 = -∞

Again, our result is not a real number so we can not determine the location of a horizontal asymptote.

Step Three: If one of or both of the limits determined above is a real number, k, then the equation of the horizontal asymptote is y=k for each unique value of k (a function can have 0, 1, or 2 horizontal asymptotes).

Since neither Step One nor Step Two resulted in a real number value for k, we can conclude that the function does not have any horizontal asymptotes.

Final Answer: The function does not have any horizontal asymptotes.

The graph of the function f(x)=(3x^2+x)/(x+2) is shown in Figure 08 below. Do you notice how there is no horizontal asymptote?

Figure 08: How to Find Horizontal Asymptotes: Not all functions will have a horizontal asymptote.

---

---

Conclusion: How to Find Horizontal Asymptotes

A horizontal asymptote of a function is an imaginary horizontal line (↔) that helps you to identify the “end behavior” of the function as it approaches the edges of a graph.

Not every function has a horizontal asymptote. Functions can have 0, 1, or 2 horizontal asymptotes.

If a function does have any horizontal asymptotes, they will be displayed as a dashed line. A horizontal asymptote is an imaginary line that is not a part of the function, and it is not a requirement to include the horizontal asymptote of a function when you graph it on the coordinate plane.

You can determine whether or not any function has horizontal asymptotes by following these three simple steps:

• Step One: Determine lim x→∞ f(x). In other words, find the limit for the function as x approaches positive ∞.

• Step Two: Determine lim x→-∞ f(x). In other words, find the limit for the function as x approaches negative ∞.

• Step Three: If one of or both of the limits determined above is a real number, k, then the equation of the horizontal asymptote is y=k for each unique value of k (a function can have 0, 1, or 2 horizontal asymptotes).

Keep Learning:

How to Find the Vertex of a Parabola in 3 Easy Steps

Learn how to find the coordinates of the vertex point of any parabola with this free step-by-step guide.

---

Exponent Rules Explained! (Free Chart)

Everything you need to know about the exponent rules!

Exponent Rules Explained

In algebra, exponent rules (also known as the laws of exponents), are a set of laws that you can use to simplify mathematical expressions that have exponents. In other words, exponent rules can be used to make complicated math expressions containing exponents much easier to work with.

Once you learn the rules of exponents, you will be able to use them to quickly and easily perform operations (adding, subtracting, multiplying, dividing, etc.) on expressions that have exponents.

The following free guide to Exponent Rules will describe and explain the rules of exponents are, what they look like, and examples of how you can use them to simplify expressions and solve math problems involving exponents.

You can use the quick links below to jump to any section of this guide, or you can follow along step-by-step.

• Quick Review: Exponents

• What are the Exponent Rules (Chart)

• Exponent Rules: Zero Exponent Rule

• Exponent Rules: Product Rule

• Exponent Rules: Quotient Rule

• Exponent Rules: Power of a Power Rule

• Exponent Rules: Power of a Product Rule

• Exponent Rules: Negative Exponent Rule

By the time that you reach the conclusion of this free guide on the rules of exponents, you will have a deep understanding of how to apply the exponent rules to simplify and solve math problems.

Are you ready to get started?

Before we start learning about the exponent rules, let’s do a quick review of exponents and cover some key vocabulary terms that you will need to be familiar with in order to make the most out of this guide.

Figure 01: The number 5 raised to a power of 3.

Quick Review: Exponents

In math, an exponent is a number or a variable at the top right of a base number or expression. The value of the exponent tells you what power the base number will be raised to.

For example, the expression 5³ has a base number of 5 and an exponent of 3. This expression means that the base number, 5, is being raised to a power of 3, meaning:

• 5³ = 5 x 5 x 5 = 125

In short, an exponent tells you how many times to multiply the base number by itself.

Now that you understand the basic definition of an exponent, it’s time to move onto learning about the Exponent Rules.

---

What are the Exponent Rules?

The rules of exponents are a collection of specific ways to simplify math expressions involving exponents.

The chart in Figure 02 below shows all of the exponent rules. You can click the link below the chart to download a PDF copy which you can print out and use as a reference whenever you need to.

Below the chart, you will find a section that explains each individual exponent rule along with examples.

Figure 02: The Exponent Rules

Click here to download your free Exponents Rules (Laws of Exponents) PDF chart.

---

Exponent Rules: Zero Exponent Rule

The first exponent rule described in this guide will be the zero exponent rule:

• a⁰=1

Figure 03: The zero exponent rule.

The zero exponent rule states that any number, variable, or expression raised to the zero power is equal to 1.

For example:

• 8⁰=1

• x⁰=1

• (a+b)⁰=1

Pretty simple, right?

To understand the zero exponent rule, you only have to remember that anything raised to the zero power is equal to one.

---

Exponent Rules: Product Rule

The next exponent rule that we will cover is called the product rule:

• a^b x a^c = a^(b+c)

Figure 04: The product exponent rule.

The product rule of exponents applies whenever you have to multiply two or more expressions that have the same base.

The rule goes as follows: whenever you have to multiply two expressions with the same base value, you can simplify the expression by adding the exponents together and keeping the base value the same.

For example:

• 4³ x 4² = 4⁵

• m² x m² = m⁴

• (a+b)⁵ x (a+b)³ = (a+b)⁸

Are you wondering where the product exponent rule comes from, let’s take a closer look at the example:

• 4³ x 4² = 4⁵

We can rewrite each individual expression as follows:

• 4³ = 4 x 4 x 4

• 4² = 4 x 4

Therefore,

• 4³ x 4² = 4 x 4 x 4 x 4 x 4 = 4⁵

The product rule allows you to simplify the expression 4³ x 4² as 4⁵. They both mean the same thing!

Before we move onto the next rule of exponents, note that the product rule only applies when the expressions have the same base value!

---

Exponent Rules: Quotient Rule

Our next stop on our chart of the rules of exponents is called the quotient rule.

The exponent rule comes into play when you have to divide two expressions with exponents that have the same base value.

The quotient rule of exponents goes as follows:

• a^b ➗ a^c = a^(b-c); or

• (a^b)/(a^c) = a^(b-c)

Figure 05(a): The quotient exponent rule with a division symbol.

Figure 05(b): The quotient exponent rule with a fraction.

Whether two expressions with the same base are being divided using a division sign (as shown in Figure 05(a)) or with a fraction (as shown in Figure 05(b)), you can simplify the expression by subtracting the second exponent from the first exponent and keeping the base value the same.

For example:

• 8⁸ ➗ 8² = 8⁶

• 8⁵ / 8² = 8³

• n¹⁰ / n⁸ = n²

• (a+b)⁹ ➗ (a+b)² = (a+b)⁷

Remember that the quotient exponent rule only applies if both expressions have the same base value.

---

Exponent Rules: Power of a Power Rule

What happens when you take an expression with an exponent and raise it to another power?

In case like this, you can use the power of a power exponent rule, which states that, whenever you have a base number, variable, or expression with an exponent raised to another exponent, the expression can be simplified by multiplying the two exponents together and keeping the base value the same.

• (a^b)^c = a^(bc)

Figure 06: The power of a power exponent rule.

Whenever you have a single base with two exponents in a row, you can simplify the expression by multiplying the two exponents together, for example:

• (9³)⁴ = 9¹²

• (y²)² = y⁴

• (x⁷)³ = x²¹

The power of a power exponent rule is a useful law of exponents that you can use to simplify complicated expressions involving multiple exponents.

---

Exponent Rules: Power of a Product Rule

What happens when you take an entire product and raise the entire thing to a power?

In cases like this, whenever you are raising a product of two numbers inside of a set of parentheses by an exponent, you can distribute the exponent and apply it to each term of the product as follows:

• (ab)^c = a^b x a^c

Figure 07: The power of a product exponent rule.

In cases when your base is a product raised to an exponent, you can distribute the exponent to each term, for example:

• (ab)³ = a³b³

• (xy²)³ = x³y⁶

• (m²n³)⁴ = m⁸n¹²

The power of a product exponent rule is one of the most important and use exponent rules on our list! Make sure that you feel comfortable with how to use it before moving onto the next law of exponents.

---

Exponent Rules: Negative Exponent Rule

The final exponent rule that we will cover in this guide is the negative exponent rule, which states that:

• a^-b = 1/(a^b)

Figure 08: The negative exponent rule.

The negative exponent rule states that any number, variable, or expression raised to a negative power can be rewritten as a fraction with one in the numerator and the same original expression in the denominator, but with the negative sign removed from the exponent.

For example:

• 8^-2 = 1/(8^2)

• x^-7 = 1/(x^7)

• (a+b)^-4 = 1/((a+b)^4)

That’s all that there is to it! If you ever have to solve a problem that requires you to give an answer that includes only positive exponents, the negative exponent rule will come in handy.

---

Conclusion: Exponent Rules

In math, you will need to be able to work with expressions that have exponents, and being able to simplify them quickly and correctly is an important skill. By learning and understanding the rules of exponents, you can easily simplify exponents in a variety of situations. Whenever you need to review the exponent rules, we encourage you to revisit this guide for a quick refresher.

Need More Help?

Check out our animated video lessons on the power to a power rule and the product to a power rule.

Keep Learning:

How to Use 'Which One Doesn't Belong?' Math Activities to Boost Engagement

How to Use ‘Which One Doesn’t Belong?’ Activities to Boost Student Engagement in K-8 Mathematics

This simple activity gives students to engage with mathematics without the fear of being incorrect.

Which One Doesn’t Belong? math activities encourage deep mathematical thinking. (Image: Mashup Math via Getty)

When students see mathematics as a black and white subject where every problem has only one correct solution, they can easily become frustrated and fearful of making mistakes.

But what would happen if students could engage with mathematics without the fear of being wrong? For example, consider the question, “What is ten minus seven?”. While it’s important that students know that the answer to this question is “Three,” it’s arguable more important (and more beneficial to their learning) that they also be able to answer a question like “Why does ten minus seven equal three?.”

These type of open-ended questions encourage deep mathematical thinking and reflection, and, since there are multiple different ways to answer them correctly, students can interact with math without the fear of making mistakes. Rather, they can think about mathematics creatively and in ways that make sense to them on a personal level.

“Open-ended math questions shift the focus from finding final answers to actually understanding whatever concept students are currently learning,” says Mashup Math founder Anthony Persico, who believes that “giving students opportunities to think about mathematics without the fear of making mistakes boosts overall engagement and participation, which encourages deep understanding and growth.”

When teachers incorporate open-ended follow-up questions in their daily lesson plans, they place a greater emphasis on thinking and learning and rather than only being concerned with whether or not students can get correct final answers to problems.

So, how can you add more open-ended math questions into your daily lessons?

Using post-it notes is a great strategy for assessing student thinking, especially when using WODB as an exit ticket. (Image: Mashup Math ST)

Which One Doesn’t Belong? Math Activities

We are all familiar with the concept of “Which One Doesn’t Belong?” (which we will abbreviate as WODB going forward). You are given a set of objects or images and you are tasked with figuring out which one of them is not like the others.

In the case of WODB math activities, students are given a set of our different numbers or images and they must determine which one of the four does not belong and then justify why their response makes sense.

How Do WODB Activities Work?

Whenever you are aiming to boost student engagement, whole-class participation, or just to mix up your instruction, simply share a four-quadrant WODB graphic that requires students to observe and reflect upon four different numbers or graphics. They will then apply their mathematical and reasoning skills to decide which of the four items does not belong and also justify why (either verbally or in writing) their choice is valid.

Since WODB activities do not have a single correct answer, students will have to organize their thoughts and provide a justified response.

Unlike typical multiple choice questions, WODB activities do not have a single correct answer. These graphics are designed to be interpreted in a variety of different ways in order to spark deep mathematical thinking and discussion (in small groups, whole class, or both).

Here's an Example:

Consider the graphic above where students have to select which of the following numbers does not belong with the other three: 11, 22, 44, and 110.

Student A says: Since 22, 44, and 110 are all divisible by two, they are all even numbers. This means that 11 does not belong because it is not divisible by two. 11 is an odd number and does not belong.

Student B says: 11 does not belong because it is a prime number. The other three numbers are not prime numbers.

Student C says: 44 does not belong because it is the only number that is divisible by 4. You can technically divide the other three numbers by 4, but the result would have a remainder, so 44 does not belong.

Student D says: The number 110 does not belong because, although it is divisible by 11 like the other numbers, it is the only three-digit number.

Notice that every student’s answer makes sense and is backed up by deep mathematical thinking. Student A and Student B both determined that 11 does not belong, but for very different reasons, while Student C chose 44 and Student D chose 110.

As teacher, you can steer this discussion in a variety of directions by asking follow-up questions like:

What justification could you use to say that 22 doesn’t belong?

What other justifications could student A have used to decide that 110 does not belong besides the fact that it is the only three-digit number?

How can students A and B both be correct?

How can students B, C, and D all be correct even though they each chose different values?

Another example of how teachers can record student responses to WODB activities. ((Image: Mashup Math ST)

What topics and grade levels are WODB activities best suited for?

WODB activities can be used for all grade levels and topics. The graphics can be topic/lesson specific or broader and more open-ended. Remember, the idea is to spark enough student thinking, interest, and curiosity at the beginning of your lesson to last for the entire class!

Are You Ready to Try WODB Activities with Your Students?

Below you will find links to download free ‘Which One Doesn’t Belong Sample Activities” that you can share in your upcoming lesson plans. All of the activities are samples from the WODB activity libraries available on our membership website.

Which One Doesn’t Belong? Numbers

Click the image to preview each sample activity and click the text link below to download your free sample worksheet.

Sample A (Grades K-2)

View fullsize

Worksheet Download

Sample B (Grades 3-5)

View fullsize

Worksheet Download

Sample C (Grades 6-8)

View fullsize

Worksheet Download

Which One Doesn’t Belong? Pictures

While numbers are a great way to introduce your students to WODB, you can also include pictures, charts, graphs, and all kinds of math-related graphics.

Click the image to preview each sample activity and click the text link below to download your free sample worksheet.

Sample A (Grades K-6)

View fullsize

Worksheet Download

Sample B (Grades 3-8)

View fullsize

Worksheet Download

Sample C (Grades 5-8)

Worksheet Download

---

WAIT! Do you want over 100 topic-specific WODB activities for grades 1-8? 🙋🏻‍♀️

Click the link below to download our best-selling PDF workbook 101 Daily 'Which One Doesn't Belong?' Activities for Grades 1-8.

---

More Math Education Resources You Will Love:

How to Find the Circumference of a Circle in 3 Easy Steps

How to Find the Circumference of a Circle

Step-by-Step Guide: What is the circumference of a circle? How to find the circumference of a circle using the formula for circumference of a circle?

Free Step-by-Step Guide: How to find the circumference of a circle explained.

Understanding how to find the circumference of a circle is an important math skill that every student must learn.

In order to learn how to find the circumference of a circle, you need to be familiar with the concept of circumference and how to use the formula for circumference of a circle to solve problems where you are tasked with finding the length of a circle’s circumference.

This free Step-by-Step Guide on How to Find the Circumference of a Circle will teach you how to use the circle formula, C=πd, to find circumference of a circle. The guide is organized by the following sections/subtopics:

• What is the Circumference of a Circle?

• Circumference of a Circle Formula

• How to Find the Circumference a Circle with Diameter

• How to Find the Circumference of a Circle with Radius

While we recommend that you work through in section in order, you can use the links above to jump to any section of interest.

Are you ready to get started? Let’s begin with a review of some important properties of circles that you will need to be familiar with in order to learn how to find the circumference of a circle.

Figure 01: Do you know the key properties of circles?

What is the Circumference of a Circle?

Before we get into what the circumference of a circle actually means, there are some key circle-related vocabulary terms that you should be familiar with:

• A circle’s diameter is any line that passes through the center point of the circle and touches two points on the edge of the circle.

• A circle’s radius is any line segment that runs from the center point and touches the edge of the circle.

• A radius of a circle, r, will always be equal to half the length of its diameter, d. In other words, r=2d.

• Conversely, the diameter of a circle, d, will always be equal to twice the length of its radius, r. In other words, d=2r.

These key properties of circles are illustrated in Figure 01 above for your reference. Make sure that you understand them well before moving on.

What is the circumference of a circle?

The circumference of a circle is the length of its outer boundary. The circumference of a circle is sometimes referred to as a perimeter of a circle and it is always measured in units such as inches, centimeters, yards, etc.

In real-world terms, you could find the circumference of a circle by taking the outer boundary of a circle and flattening it out into a straight line and then measuring the length of that straight line. Whatever the length is would be the circumference of the circle.

For example, if you have a section of rope that was 4 feet long and you curled it into a perfect circle, the circle will also have a circumference of 4 feet, as shown in Figure 02 below.

Figure 02: What is the circumference of a circle?

The biggest takeaway here is that the circumference of a circle is the total length of the outer region of the circle. You could imagine taking a circle, cutting it somewhere, and then bending it so it forms a straight line. You could then find the circumference by measuring that straight line.

The diagram in Figure 03 below further illustrates the concept of circumference in mathematical terms.

Now that you understand what the circumference of a circle represents, let’s move onto the next section, where will we learn the circumference of a circle formula.

Figure 03: What is the circumference of a circle?

Circumference of a Circle Formula: C=πd

You can find the circumference of any circle simply by using the circumference of a circle formula: C=πd (where d is the length of the diameter of the circle).

In other words, circumference equals pi times diameter.

Whenever you are using the circumference of a circle formula, you have the option of using pi (π) or an approximation of pi (π≈3.14). If you have a calculator that has a π button, we highly recommend using it instead of approximating pi as 3.14, since it will give you more accurate answers. However, both options are acceptable in most cases.

Before continuing onto the next section, be sure to remember that the d in the circumference formula represents the length of the circle’s diameter. You can use the diagram in Figure 04 below as a reference for remembering that the circumference of a circle formula is C=πd.

Figure 04: The circumference of a circle formula is C=πd (circumference equals pi times diameter).

For example, let’s say that we wanted to find the circumference of a circle with a diameter of 10 cm. Knowing that d=10 in this example, we could solve this problem by using the circumference of a circle formula as follows:

• C=πd and d=10

• C=π(10) or C=10π

• C=31.41592654…

• C=31.4 cm

So, we can conclude that the circle has an approximate circumference of 31.4 centimeters. We figured this out by substituting d with 10 in the formula to get C=π(10) or C=10π (this both mean the same thing—the product of 10 and π) and using our calculator to get C=31.41592654…, which we rounded to the nearest tenth decimal place to get C=31.4 cm.

Note that we will be expressing circumference to the nearest tenth of decimal place for all of the examples in this guide.

The step-by-step process for finding the circumference of a circle with a diameter of 10cm is shown in Figure 05 below.

Figure 05: How to use circumference of a circle formula.

Now that you know how to use the circumference formula, you are ready to learn how to find the circumference of a circle by working through a several examples.

---

How to Find Circumference of a Circle with Diameter

In the previous section, we learned how to find the circumference of a circle with diameter of 10cm. The step-by-step process for solving thing problem is illustrated in Figure 05 above.

As long as you know that the circle circumference formula is C=πd, you can solve any problem where you have to find the circumference of a circle with diameter given. To do this, simply substitute d with the numerical value of the length of the diameter and then multiply it by π to determine the length of the circle’s circumference.

This method is exactly how we will solve our first practice problem. Let’s go ahead and get started.

Example #1: Find the Circumference of a Circle with Diameter 17 mm

For this first example, we have to find the circumference of a circle with diameter of 17 mm.

We can solve this problem by using the circumference of a circle formula, C=πd, by inputting d=17 into the formula and solving as follows:

• C=πd

• C=π(17) pr C=17π

• C=53.40707511…

• C=54.4 mm

Final Answer: The circle has a circumference of 54.4 mm.

Finished! As long as you know the length of a circle’s diameter, you can input it into the circle circumference formula to calculate its circumference.

The step-by-step process for solving Example #1 are shown in Figure 06 below. Be sure that you are comfortable with this process before moving onto the next example.

Figure 06: How to Find the Circumference of a Circle Step-by-Step.

Example #2: Find the Circumference of a Circle with Diameter 20.6 yd

For this next example, we want to calculate the circumference of a circle with diameter 20.6 yd.

Notice that the value of the diameter, d, in this example is a decimal. However, you can still use the formula, C=πd, to solve this problem and find the circumference of the circle as follows:

• C=πd

• C=π(20.6) or C=20.6π

• C=64.71680866…

• C=64.7 yd

Final Answer: The circle has a circumference of 64.7 yd.

This process for using the circumference of a circle formula to find the circumference of a circle with a diameter of 20.6 yd is illustrated in Figure 06 below.

Figure 06: How to find the circumference of a circle when the diameter is given.

Now, let’s work through one more example of how to find circumference of a circle with diameter in a real-world context.

Example #3: Find the Circumference of a Circle with Diameter 60 meters

For this third example, we want to find the circumference of a paved sidewalk that surrounds a circular pond with a diameter that is 60 meters long.

Even though this is a real-world scenario, we can still use the circumference formula to find the answer as follows:

• C=πd

• C=π(60) or C=60π

• C=188.4955592…

• C=188.5 m

Final Answer: The paved sidewalk has a circumference of 188.5 meters.

The diagram in Figure 07 illustrates this real-world scenario and how we used our formula to figure out the circumference of the path that surrounds the circular pond.

Figure 07: How to find the circumference of a circle in a real-world scenario.

---

How to Find Circumference of a Circle with Radius

You probably have learned that finding the circumference of a circle when you are given the length of its diameter is a pretty straightforward process, but what happens when only know the length of the circle’s radius and not the length of its diameter?

As long as you understand the relationship between a circle’s radius and its diameter, you can easily use a given radius to figure out the length of the diameter. And this skill is extremely useful because it will allow you to use the circumference of a circle formula, C=πd, to solve circle problems where only the radius is given.

Recall from our vocabulary review at the start of this guide that a radius of a circle is any line segment that starts at the center and ends on the edge of the circle and that the radius of a circle is equal to half the length of the circle’s diameter.

• r = d/2

Conversely, we can say that the diameter of a circle is equal to twice the length of its radius:

• d=2r

So, if you know the length of the radius of a circle, you can use it to find the length of the diameter, d, by multiplying it by 2.

For example, if you were given a circle with a radius of 5 feet (r=5). You could take the radius and double it to find the value of the diameter, which, in this case, would be 10 ft.

• r=5

• d=2r

• d=2(5)

• d=10

The diagram in Figure 08 below illustrates this relationship between the radius and the diameter of a circle.

The key takeaway is that the diameter of a circle is equal to twice the length of its radius.

Now, let’s go ahead and apply our understanding of this relationship to another practice problem.

Figure 08: The diameter of a circle is equal to twice the length of its radius (d=2r).

Example #4: Find the Circumference of a Circle with Radius of 7 inches

In this example, we have to find the circumference of a circle with a radius of 7 inches (r=7).

Our goal is to solve this problem the same way that we solved the three previous examples where we calculated circumference using the formula C=πd.

However, the difference between Example #4 and the previous three is that, in this case, we are given the radius of the circle, r, and not the diameter.

But we can use the given radius, r=7, to find the length of the diameter, d, because we know that the diameter of a circle is equal to twice the length of its radius:

• d=2r

• d=2(7)

• d=14

Therefore, if the circle has a radius of 7 inches, then it also has a diameter of 14 inches (because 7x2=14).

Now that we know the value of d (d=14 in this case), we can substitute it into the circumference of a circle formula and solve as follows:

• C=πd

• C=π(14) or C=14π

• C=43.98229715

• C=44.0 in

Final Answer: The circle has a circumference of 44 inches.

The entire step-by-step process for solving this fourth and final example are illustrated in Figure 09 below. If you are still confused about how to find the circumference of a circle, we recommend that you go back and work through the practice problems again.

Figure 09: How to find the circumference of a circle with a given radius.

---

How to Find the Circumference of a Circle: Conclusion

The circumference of a circle, also known as its perimeter, is the length of its outer boundary.

Understanding how to find the circumference of a circle is a foundational math skill that has many practical applications both inside and outside of the math classroom.

Whenever you have to find the circumference of a circle, you can use the formula C=πd, where d represents the lengths of the circle’s diameter, to find an answer.

If you are given the length of the circle’s diameter, you can substitute it for d in the formula and solve. However, if you only know the circle’s radius, you will have to multiply it by two (d=2r) to find the length of its diameter, d, before you can use the formula.

However, as long as you know the circumference of a circle formula and the relationship between the radius and diameter of a circle, you can easily calculate the circumference of a circle in just a few simple steps.

Keep Learning:

How to Find the Area of a Circle in 3 Easy Steps

---